題目難度和冗余信息對代數應用題信息區分策略影響的實驗研究

岳寶霞，蘇 穎，馮 虹

（1.天津師范大學 教師教育學院，天津 300387；2.天津市耀華中學，天津 300040；3.天津師范大學 教育科學學院，天津 300387）

1 問題提出

應用題是應用數學問題的簡稱，也稱為文字題（word problem），是用自然語言表達的數學問題，需要解題者將自然語言文字轉化為“數學符號構成的算式”，然后用數學方法求解.

已有研究表明，小學加減應用題的難度對學生解題影響顯著[1～3].Decorte等人的研究表明，題目語義結構對不同學業程度解題者的解題過程會產生影響[4].早期研究表明，當題目中含有冗余信息時，解題者區分相關和無關信息更加困難[5～6].所謂冗余信息即題目中含有的多余條件或無關信息，通常情況下，題目中的信息均為解題必要信息，如果在題目中插入冗余信息便會增加題目的難度.盡管研究表明，插入無關信息通常導致解題錯誤，但沒有指出兒童區分信息并形成有用表征的過程是怎樣的[7].

分析已有文獻發現，以往的研究大多強調解應用題過程的內在表征，很少關注解題者使用了怎樣的信息區分策略來區分有用的和無關的信息[7].信息區分策略指學生在解題過程中將題目背景及問題分析成語義單元，對信息類型進行檢驗、區分，找出信息之間的相關性，目的是對這些信息進行比較進而與題目中的問題相匹配.對參與實驗的學生的眼動軌跡進行分析發現，學生共使用了5種區分策略：重讀題目策略，單一比較策略，以特征為基礎策略，問題—引導策略和首次讀題區分策略.

已有研究中實驗材料多為算數應用題，極少涉及代數應用題.曾有研究發現，初中生從研究具體數字到學習用字母表示數和未知元，會出現認知上的困難[8].因為算術在很大程度上是過程性的，所以學生習慣于思考用于解決問題的運算，而不是思考應該用來表征問題情境之間關系的運算.因此，研究代數應用題解題過程具有實踐意義.在研究方法上，Littlefield等人使用了計算機軟件輔助、口語報告等方法，均有其局限性[7，9～10].研究將以初二年級學生為實驗對象，對不同數學成績學生使用的信息區分策略進行分析.在實驗方法上，采用眼動分析技術，考察學生在題目自然呈現的條件下對幾種信息區分策略的使用情況[11～20].

2 方 法

2.1 被 試

對學生數學成績的高、低分組按照以下標準進行：

（1）以初一數學成績的學年總評和初二的第一次數學統考成績為指標，年級前15%的學生為數學成績高分組的候選人，居于年級后15%的學生為數學成績低分組的候選人.

（2）教師評定，班主任和數學教師根據候選學生的平時表現，對他們進行高分組和低分組的劃分.最終在初中二年級選擇數學成績高分組和低分組被試各16名，共32名被試，平均年齡為14±0.98歲.所有被試的智力、視力均正常.為了避免兩組被試閱讀理解能力的差異對題目理解的影響，對兩組被試初二的第一次語文統考成績進行了檢驗，結果表明，數學成績高分組與低分組學生的語文成績不具有顯著差異.

2.2 實驗材料

實驗前先用30道題目對不參加實驗的初中二年級兩個班的學生進行測試（其中一半題目不含冗余信息，一半題目包含冗余信息），要求他們解題后對題目的難度進行兩個等級的評定，即較容易、較難.然后請中學數學教師做相同項目的評定.將學生與教師的評定結果進行比較，從評定結果一致的4種類型題目中各隨機抽取兩道題，構成實驗材料.

實驗材料包括練習材料和正式實驗材料.練習材料是與正式實驗材料長度一致的較簡單代數應用題.題目內容以初中二年級水平數學教材為基礎，題目長度大致相同.正式實驗材料共包括8道代數應用題.分為4種類型：較易的不含冗余信息的題目，較易的含有冗余信息的題目；較難的不含冗余信息的題目，較難的含有冗余信息的題目.

2.3 實驗設計

采用2（數學成績）×2（題目難度水平）×2（冗余信息：含、不含）的3因素混合實驗設計.數學成績為被試間因素，題目難度與冗余信息為被試內因素.

2.4 實驗儀器

研究使用了Tobbi120型眼動儀.

2.5 實驗程序

整個實驗在實驗室里進行.被試坐在顯示器正前方，眼睛距離屏幕中心60 cm.實驗有兩名主試，一名負責操作眼動儀，另一名負責用錄音筆記錄被試的口語報告.實驗指導語如下：同學你好，今天請你來做一個實驗，目的是了解你怎樣做題.做好解題準備后請按鼠標，屏幕上會出現一道應用題，你只需列出算式，不用計算結果.一旦你覺得能夠列出算式，請立即按下鼠標，然后口頭報告出算式并說出你的解題思路.如果你不會解這道題，也請你按下鼠標，繼續進行下一題.開始實驗前，主試先進行示范，并要求被試對練習材料報告解題計劃.在確認被試明白指導語的要求后，開始正式實驗.

2.6 眼動記錄指標

眼動儀記錄以下指標作為因變量：

（1）眼動軌跡：解題者對題目注視的全部眼動過程，包括眼跳、回視及注視點在某處停留時間等.為考察學生采用的信息區分策略，在Littlefield等人工作的基礎上對5種策略進行分析，并分析每個學生的眼動軌跡，最后由專家和中學教師評定.

① 重讀題目（rereading）策略：通過重復地閱讀題目，將部分信息及語義特征貯存到工作記憶中，然后對信息進行比較，使用“重讀題目”策略的被試，可能是整篇重讀也可能是整句重讀，但不管怎樣回視次數會很多.

② 單一比較（simple comparison）策略：使用單一比較策略的被試在數字及關系詞之間進行簡單直接的比較，解題者可能會根據問題部分的要求直接列出方程.

③ 以特征為基礎（featurally-based）策略：在題目中尋找與問題中的語義相匹配的語義特征，通常會將注視點集中在變量名或與問題部分相似的事件、概念上，如：速度、長度、工程施工等.

④ 問題—引導（question-guided）策略：以問題中的語義詞語為指導，對信息進行分析，使用“問題引導”策略的被試，注視點經常回到問題區域.

⑤ 首次讀題（discriminate during initial reading）區分策略：首次讀題后就對語義類型進行了區分，找到解題所需的關鍵信息，注視點集中在關鍵信息和相關數字信息上，如：“…的速度比…的速度快…”，“比原計劃提前*天”等；且總注視次數顯著少于其他的策略.

（2）注視點出入次數：指被試在某個興趣區的注視點出入的次數.

興趣區的劃分：實驗將含有冗余信息的題目劃分為 7個興趣區，即題目、相關數字、無關數字、相關事件及行為、無關事件及行為、關鍵信息、問題（較易題目含有一個無關數字，較難題目含有兩個無關數字）；將不含冗余信息的題目劃分為5個興趣區，即題目、相關數字，相關事件及行為、關鍵信息、問題（較易題目含有2～3個相關數字，較難題目含有4個相關數字）.其中相關數字指在問題表述中對計算正確答案必需的數字；無關數字指在題目表述中出現的，對計算正確答案無用的數字.

2.7 實驗結果的統計

采用SPSS for Windows 16.0統計包進行處理.

3 結果分析

3.1 題目難度和冗余信息對不同成績學生信息區分策略的影響

根據學生的眼動軌跡，分析被試解題過程中采用的信息區分策略，并記錄下不同成績學生解不同類型題目時采用的一種或幾種信息區分策略，每種信息區分策略使用頻率見表1.

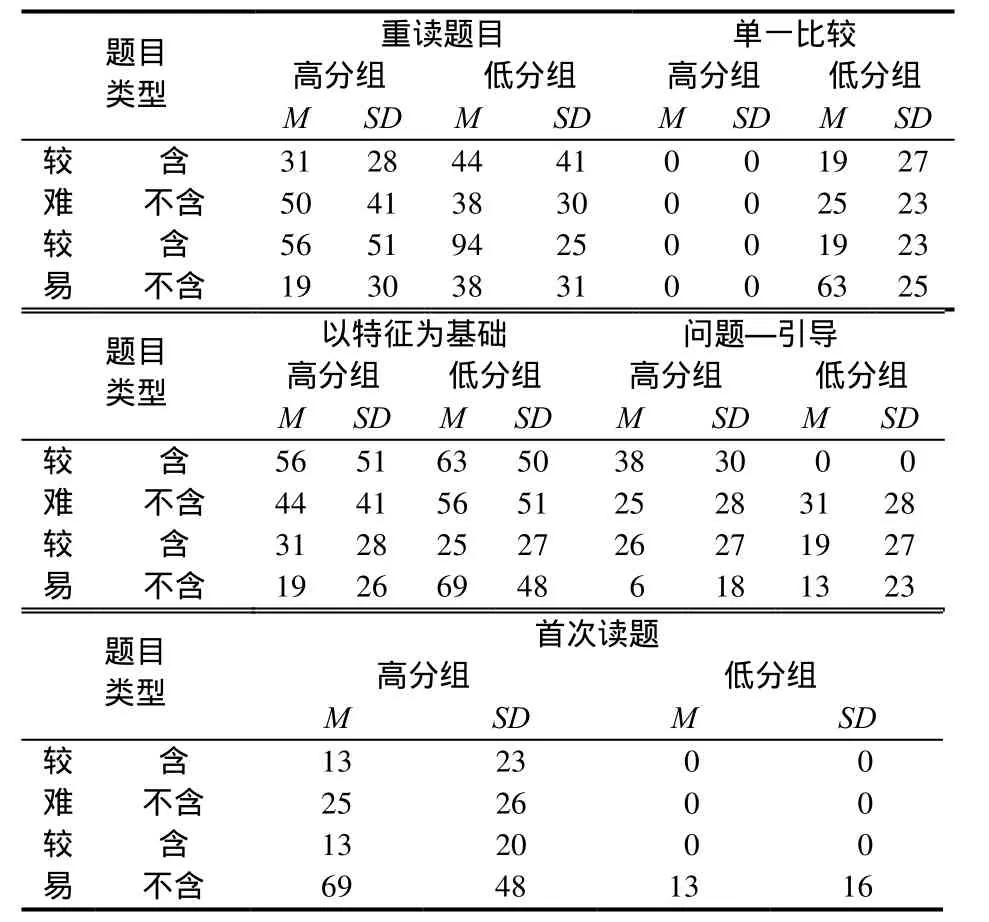
表1 不同成績學生解不同類型題目時采用的信息區分策略百分比（%）

對不同成績學生解題時信息區分策略使用頻率進行重復測量方差分析，結果如下.

（1）重讀題目策略：冗余信息的主效應顯著F(1,30)=7.848，p=0.009，即題目含有冗余信息時解題者使用重讀策略的頻率顯著高于不含冗余信息題目.題目難度和冗余信息的交互作用顯著F(1, 30)=12.350，p=0.001.簡單效應分析結果顯示：對于較難題目，無論是否含有冗余信息，解題者使用重讀策略頻率的差異不顯著；對于較易題目，使用重讀策略的頻率在冗余信息間存在顯著差異t(31)=4.676，p=0.000，即解含有冗余信息的易題時使用重讀策略的次數多于解不含冗余信息的題目.

（2）單一比較策略：數學成績的主效應顯著F(1,30)=4.84，p=0.036，即低分組學生使用單一比較策略的頻率顯著高于高分組學生；題目難度和是否含有冗余信息的主效應不顯著.3因素間的交互作用不顯著.

（3）以特征為基礎策略：數學成績和冗余信息的主效應不顯著，題目難度的主效應顯著F(1, 30)=5.870，p=0.022，即被試解較難題目時使用該策略的頻率顯著高于較易題目.3因素間的交互作用不顯著.

（4）問題—引導策略：數學成績、題目難度和是否含有冗余信息的主效應均不顯著.數學成績和冗余信息的交互作用顯著F冗余*成績(1, 30)=6.106，p=0.019.簡單效應分析結果顯示：對于高分組學生，其使用問題—引導策略的頻率在冗余信息間差異不顯著；對于低分組學生，使用問題—引導策略的頻率在冗余信息間存在顯著差異t(31)=-2.236，p=0.041，即解不含冗余信息的題目時使用問題—引導策略的頻率顯著多于解含有冗余信息的題目.

（5）首次讀題區分策略：數學成績的主效應顯著F(1,30)=33.092，p=0.000，即高分組學生使用首次讀題策略的頻率高于低分組學生；題目難度的主效應顯著F(1, 30)=6.497，p=0.016；即被試解較易題時使用該策略的頻率高于較難題；冗余信息的主效應不顯著.數學成績和冗余信息的交互作用顯著F冗余*成績(1, 30)=10.565，p=0.003.簡單效應分析結果顯示：對于高分組學生，使用首次讀題區分策略的頻率在冗余信息間存在顯著差異t(31)=-4.568，p=0.01，即解不含冗余信息題目時使用首次讀題策略的次數多于解含有冗余信息題目；對于低分組學生，該差異不顯著.

3.2 題目難度和冗余信息對不同成績學生出入“問題”區域次數的影響

研究記錄了被試對題目中“問題”的注視次數及注視點移動軌跡，得到了被試出入“問題”區域次數，不同數學成績學生解不同類型代數應用題時進出“問題”區域次數如表2.

對學生解題時進出“問題”區域次數進行重復測量方差分析，發現冗余信息主效應顯著F(1, 30)=4.439，p=0.044，即學生解含有冗余信息題目時注視點進出“問題”區域的次數顯著高于不含冗余信息題目.數學成績和冗余信息的交互作用邊緣顯著F(1, 30)=3.456，p=0.073.簡單效應分析顯示：對于高分組學生，其注視點進出“問題”區域的次數在冗余信息上邊緣顯著t(15)=2.085，p=0.055，即當題目含有冗余信息時，學生進出“問題”區域的次數多于不含冗余信息的題目；對于低分組學生其差異不顯著.

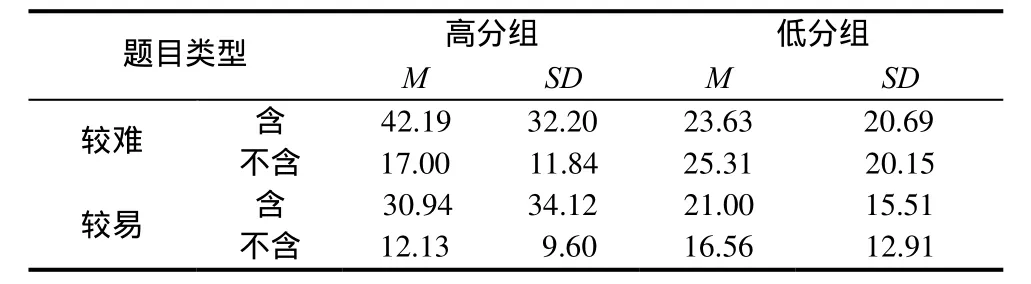
表2 不同數學成績學生對不同類型題目進出“問題”區域的次數

3.3 題目難度和冗余信息對不同成績學生表征“關鍵信息”的影響

研究記錄了被試對題目中“關鍵信息”的注視點移動軌跡，得到了被試進出“關鍵信息”區域的次數，具體情況見表3.

對不同數學成績學生進出“關鍵信息”區域的次數進行重復測量方差分析，結果表明：題目難度的主效應顯著，F=9.105，p<0.005，冗余信息的主效應顯著F=12.531，p<0.001，數學成績、題目難度和冗余信息的交互作用邊緣顯著F=3.436，p=0.074.簡單效應分析顯示：無論題目難易，高分組學生進出“關鍵信息”區域的次數在冗余信息間都存在顯著差異t較難=2.695，p<0.05，t較易=2.178，p<0.05；低分組學生解較易題時，進出“關鍵信息”區域的次數在冗余信息間存在顯著差異t=2.046，p<0.05.

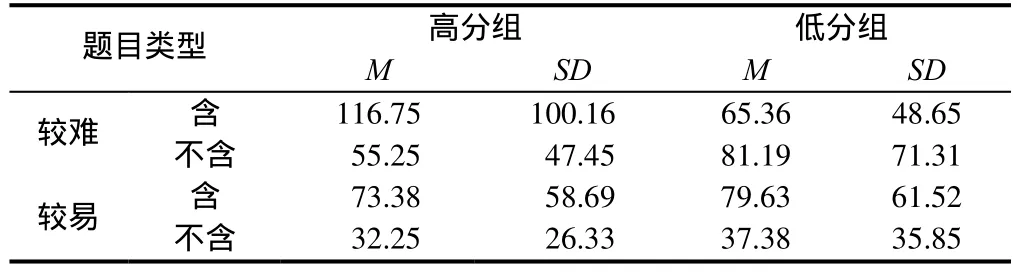
表3 不同成績學生對不同類型題目進出“關鍵信息”區域的次數

4 討 論

研究記錄了不同成績學生解不同類型題目時采用的一種或幾種信息區分策略，對每種信息區分策略使用頻率進行了統計，用來分析每種區分策略的使用受到哪些因素的影響.同時考察了被試在“問題”區域及“關鍵信息”區域注視點的進出次數，用來輔助說明被試對區分策略是否進行了調整.

4.1 幾種信息區分策略的使用情況

重讀題目策略使用頻率較高，當題目較容易且含有冗余信息時，使用該策略的次數顯著多于不含冗余信息的題目.說明對于易題，學生對冗余信息更加敏感，會因是否插入冗余信息調整該策略的使用.但當題目較難時，是否含有冗余信息對該策略的使用頻率沒有影響，原因可能是題目本身語意結構更加復雜，解題者需要使用多種信息區分策略從而降低了重讀的使用頻率.

高分組學生不使用單一比較策略，低分組學生在各種類型題目中都有使用，但使用的頻率較低，且不受題目難度及冗余信息的影響.原因可能是使用該策略的低分組學生不會隨題目類型的變化調整區分策略.

特征比較策略的使用頻率也比較高，同時受題目難度的影響明顯.即解難題時的使用次數多于易題，原因可能是當題目語義結構復雜時，解題者需要對題目中的情境信息進行更多的加工，如人物、變量、事件等.

對于問題—引導策略不同成績學生都會使用，低分組學生在解不含冗余信息題目時使用該策略頻率多于含冗余信息題目，但高分組學生不會因題目類型不同而對該策略的使用進行調整.

高分組學生在使用首次讀題區分策略時會因題目類型不同進行調整，即解容易題時使用的次數多于難題，解不含冗余信息題目時使用次數多于含冗余信息題目.說明首次讀題區分策略適用于語意結構較簡單的題目，對于高分組學生來說題目中變量關系較為明顯，首次讀題后就能找到解題的關鍵要素.

4.2 題目難度和冗余信息對學生使用信息區分策略的影響

4.2.1 題目難度和冗余信息對低分組學生使用信息區分策略的影響

Littlefield研究認為，冗余信息可能會增加錯誤推理和情境中細節推斷的錯誤率，或者會降低選擇、整合有用信息的可能性.高分組會隨題目難度變化調整區分策略，低分組則不作調整.研究的結果表明：

（1）由表3可知，當題目較容易時，含有冗余信息對低分組學生進出“關鍵信息”的次數會有影響.說明對于語義結構不太復雜的題目學生能夠找出解題的關鍵要素，部分學生使用了首次讀題區分策略.但當題目插入冗余信息時，低分組使用首次讀題區分策略的比率為0.另外由表2知，無論題目難易含有冗余信息對低分組學生進出“問題”區域的次數都沒有影響，表1顯示低分組學生解含有冗余信息題目時，使用問題—引導策略的次數顯著多于解不含冗余信息題目.原因可能是學生在解不含冗余信息題目時更多地使用了重讀策略，因為兩種策略的使用都會使得問題區域注視點出入次數增加.

（2）當題目較難時，是否含有冗余信息對低分組學生進出“問題”及“關鍵信息”區域的次數均無影響.這與表1中所示，低分組在問題—引導策略及首次讀題區分策略的使用上不因題目是否含有冗余信息而存在差異的結果一致.說明當題目難度增大時，題目本身的語義結構更加復雜，低分組學生不會因題目類型不同而對信息區分策略進行調整.

4.2.2 題目難度和冗余信息對高分組學生使用信息區分策略的影響

實驗結果表明，高分組學生對題目的難度及是否含有冗余信息更加敏感.

（1）無論題目是難還是易，冗余信息對高分組學生進出“問題”區域的次數都有影響.即當題目含有冗余信息時，高分組學生的注視點出入“問題”區域的次數顯著多于不含冗余信息的題目.表1的結果顯示，高分組學生不會因題目是否含有冗余信息而對問題—引導策略的使用進行調整，說明對于含有冗余信息的題目，高分組學生可能更多地使用了重讀題目等策略.因為幾種策略的使用都有可能使得“問題”區域注視點進出次數增加.

（2）無論題目是難還是易，高分組學生進出“關鍵信息”區域的次數在冗余信息間都存在顯著差異.當題目含有冗余信息時，高分組學生進出“關鍵信息”的次數增多.這說明高分組學生對冗余信息更加敏感，當題目插入冗余信息時，他們會在冗余信息與解題的關鍵信息之間進行比較，通過對題目“關鍵信息”的分析區分有用和無用信息，從而導致該區域注視點出入次數的增加.

5 結論及教學建議

5.1 結 論

由以上的實驗研究可以得到如下結論：不同成績學生解題時會使用不同的信息區分策略，但高分組學生不使用單一比較策略，低分組學生則很少使用首次讀題區分策略.低分組學生解較容易題目時會因題目是否含有冗余信息調整區分策略，但當題目難度增大時則不作調整；高分組學生會因題目難度及是否含有冗余信息調整區分策略.

5.2 教學建議

難題及含有冗余信息的題目增加了題目語意信息的復雜性，增加了問題表征的難度.低分組學生更容易受到影響，而高分組學生對語意信息更加敏感，對信息區分策略的使用更加靈活.在應用題解題教學的過程中教師可以有意識的加強信息區分策略的指導，比如：一道代數應用題中有哪些語意類型（事件、人物、變量、測量單位）的信息？如何找出它們之間的關系？與問題部分的語意信息以何種方式相關？等等.特別是對于低分組學生而言，加強對學生數學閱讀理解能力的培養.指導學生分析語意信息之間的特征及關系，而不是將關注點只放在變量、數字及關鍵詞上.

[1] Hegarty M, Mayer R E, Christopher A M. Comprehension of Arithmetic Word Problems: A Comparison of Successful and Unsuccessful Problem Solvers [J]. Journal of Educational Psychology, 1995, 87(1): 18.

[2] 陳英和，仲寧寧，田國勝，等.小學2～4年級兒童數學應用題表征策略差異的研究[J].心理發展與教育，2004，（4）：19-24.

[3] 馮虹，安蓉，陰國恩.比較應用題的問題表征研究[J].天津師范大學學報，2007，（4）：40-43.

[4] De Corte E, Verschaffel I, Pauwel A. Influence of the Semantic Structure of Word Problems on Second Graders’ Eye Movements [J]. Journal of Educational Psychology, 1990, 82(2): 359-365.

[5] Low R, Over R. Gender Differences in Solution of Algebraic Word Problems Containing Irrelevant Information [J].Journal of Educational Psychology, 1993, 85(2):331.

[6] Muth K D. Extraneous Information and Extra Steps in Arithmetic Word Problems [J]. Contemporary Educational Psychology, 1992, 17(3): 278-285.

[7] Littlefield J, Riser J J. Finding the Critical Facts: Children’s Visual Scan Patterns when Solving Story Problems that Contain Irrelevant Information [J]. Journal of Educational Psychology, 2005, 97(2): 224-234.

[8] Nicole M McNeil, Bethany Rittle-Johnson, Shanta Hattikudur, et al. Continuity in Representation between Children and Adults: Arithmetic Knowledge Hinders Undergraduates’ Algebraic Problem Solving [J]. Journal of Cognition and Development, 2010, 11 (4):437.

[9] Littlefield J, Riser J J. Semantic Features of Similarity and Children’s Strategies for Identification of Relevant Information in Mathematical Story Problems [J]. Cognition and instruction, 1993, (11): 133-188.

[10] Littlefield J. College Students and Algebra Story Problems: Strategies for Identifying Relevant Information [J]. Reading Psychology, 2006, (2): 6～9.

[11] 岳寶霞，馮虹.眼動分析法在數學應用題解題研究中的應用[J].數學教育學報，2013，22（1）：93-95.

[12] 黃秦安，劉達卓，聶曉穎.論數學欣賞的“含義”“對象”與“功能”——數學教育中的數學欣賞問題[J].數學教育學報，2013，22（1）：8-12.

[13] 徐文彬.試論數學文化視域中的數學學習[J].數學教育學報，2013，22（1）：13-17.

[14] 王名揚，徐瀝泉，徐利治.論一種緣自認知心理學及教育學研究的數學認知過程[J].數學教育學報，2013，22（1）：33-36.

[15] 謝圣英，喻平.數學教育中的隱喻研究[J].數學教育學報，2013，22（2）：5-10.

[16] 費祥歷，許曉婕.數學文化教育的思考與實踐[J].數學教育學報，2012，21（1）：13.

[17] 徐文彬.關于現實社會中兒童學習若干現象的檢討——以“科學數學觀”視域下數學學習為案例分析[J].數學教育學報，2012，21（1）：17-20.

[18] 劉振達，王青建，邵茹.從數學史角度研究數學學習動機[J].數學教育學報，2012，21（3）：26-27.

[19] 袁智強.整合技術的學科教學知識研究綜述[J].數學教育學報，2012，21（6）：13-18.

[20] 彭瑜，徐速.不同數學學業成就初中生數學焦慮的研究[J].數學教育學報，2012，21（4）：40-43.