BP神經網絡在溫度二次儀表零位電壓補償的應用

石良喜

（廣州計量檢測技術研究院，廣東廣州 510030）

0 引言

溫度二次儀表在各行業中使用相當廣泛，隨著使用環境的改變，其內部環境的溫度也會改變，導致溫度二次儀表內部傳感器原件及集成電路板零位電壓產生漂移，從而產生溫度二次儀表的測量誤差，因此有必要進行溫度補償，減少測量誤差。本文選用數字傳感器DS18B20對二次儀表所處的環境溫度進行測量，運用人工神經網絡與BP算法相結合，得出非線性溫度補償數據列表。利用MATLAB工具，對二次儀表的零位測量電壓的溫度漂移進行補償，通過模擬仿真，對比分析補償前后的測量結果，使用該方法，提高了溫度二次儀表的測量精度，減少了系統的測量誤差，對二次儀表的計量性能起著重要作用。

1 二次儀表的零位電壓溫度特性測量

針對二次儀表的使用環境，二次儀表內部環境溫度的測量，測試溫度為-40℃～80℃，在輸入為零的條件下，利用單片機模塊來采樣二次儀表的零位電壓值。零位電壓溫度特性的測量系統如圖1，ADC及DAC分別采用A/D轉換器和D/A轉換器，可以采用獨立的A/D及D/A芯片[1]，本文中分別指單片機中的A/D和D/A模塊。

圖1 二次儀表零位電壓溫度特性測量系統框圖

硬件電路的設計，具體如圖2所示。這里主要選用數字溫度傳感器DS18B20與單片機89C51作為主元件，數字溫度傳感器DS18B20工作方式為外部電源供電方式，與單片機89C5的P1.7管腳相連；整個的硬件電路較簡單，只需要外接入一個4.7kΩ的電阻，即可實現二次儀表零位電壓溫度特性的測量。

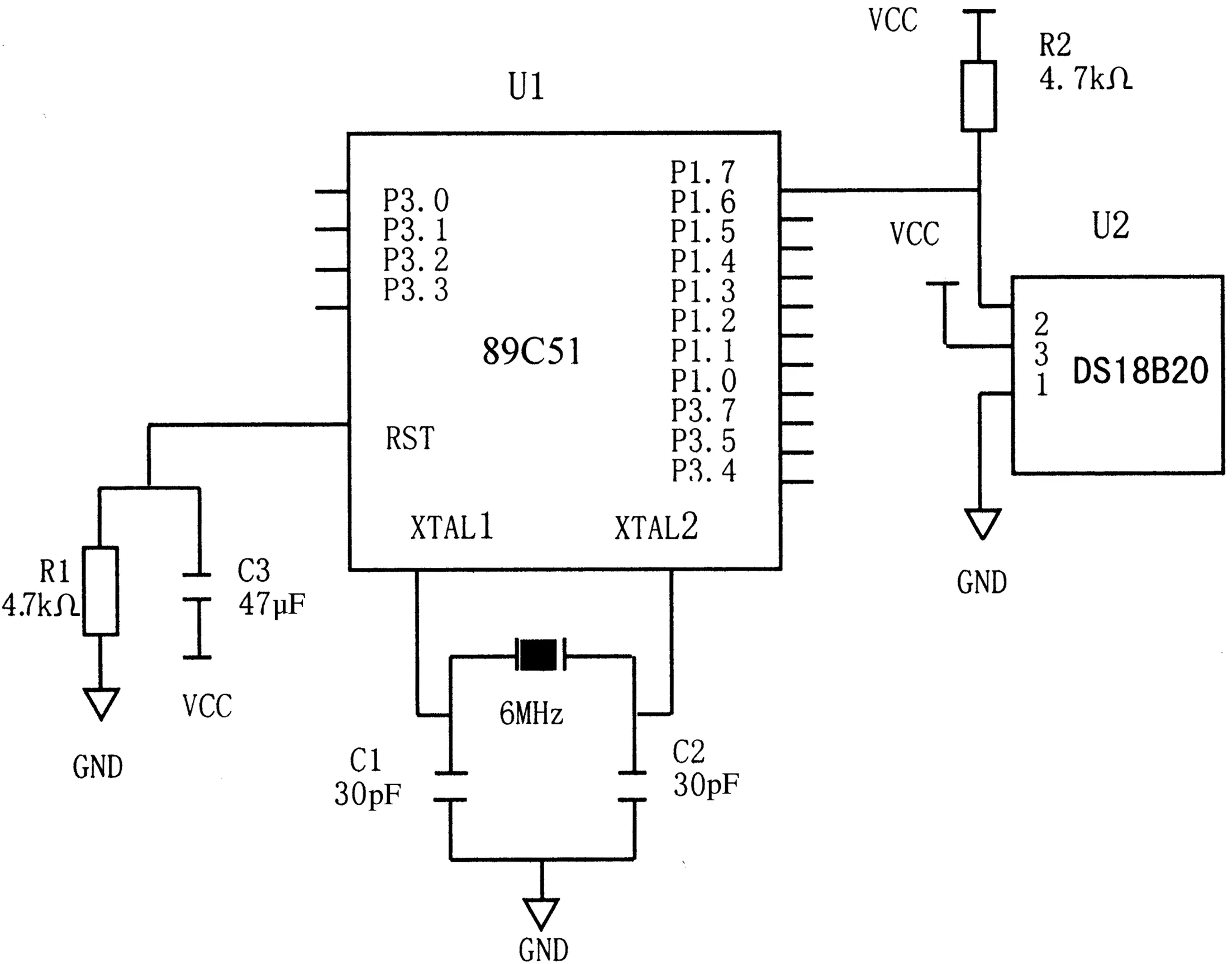
圖2 零位電壓溫度特性測量電路連接圖

通過測試，得出零位電壓溫度特性曲線如圖3所示。

圖3 零位電壓溫度特性曲線圖

由圖3可知，該二次儀表的零位電壓溫度特性呈非線性，特性曲線規律性不明顯。通常采用的方法有硬件法和軟件法，但硬件法存在調試困難[2]，補償的效果不明顯的缺點，一般采用軟件法尤其是人工智能法可以彌足這些不足[3]。

2 零位電壓溫度漂移補償方案

針對二次儀表的零位電壓溫度特性呈非線性，為了有利于輸入信號的數字處理，這里運用人工神經網絡，采用BP算法，利用BP神經網絡的非線性擬合和泛化能力，可以有效地對二次儀表的零位電壓進行非線性補償。具體方案如圖4所示。

二次儀表在零輸入的條件下，即所檢測到的信號為零，X=0。利用DS182B20及信號調理電路，采用在不同溫度條件下傳感器的溫度特性，得到二次儀表的傳感器的溫度特性為

圖4 零位電壓溫度漂移補償框圖

Y（x，t）=Y（0，t）；t=t1，t2，t3……，tn

利用采樣數據設計人工神經網絡結構，編寫程序，訓練人工神經網絡，對二次儀表的溫度特性進行擬合，得到溫度范圍內任意溫度下二次儀表零位電壓的溫度特性擬合數據[4]。訓練后的人工神經網絡特性為T=f（t），t為任意值。由于人工神經網絡具有非線性擬合能力和泛化能力，把任意溫度下傳感器零位下電壓的輸出作為人工神經網絡的訓練目標值，經過訓練以后，得到

T=f（t）=Y（0，t），t為任意值，即 T-Y=U（t）=0，從而傳感器的零位電壓得到補償。

3 補償模塊設計及仿真

根據圖4所示的補償系統框圖搭建二次儀表零位值的溫漂補償模塊，如圖5所示。圖5中，input3為補償前的傳感器輸出；display1為補償后的二次儀表的輸出值；display2為補償值；dis?play3為人工神經網絡模塊的輸出。其中input2為20℃時的電平值，由二次儀表感溫部分產生的電壓作為基準電壓。

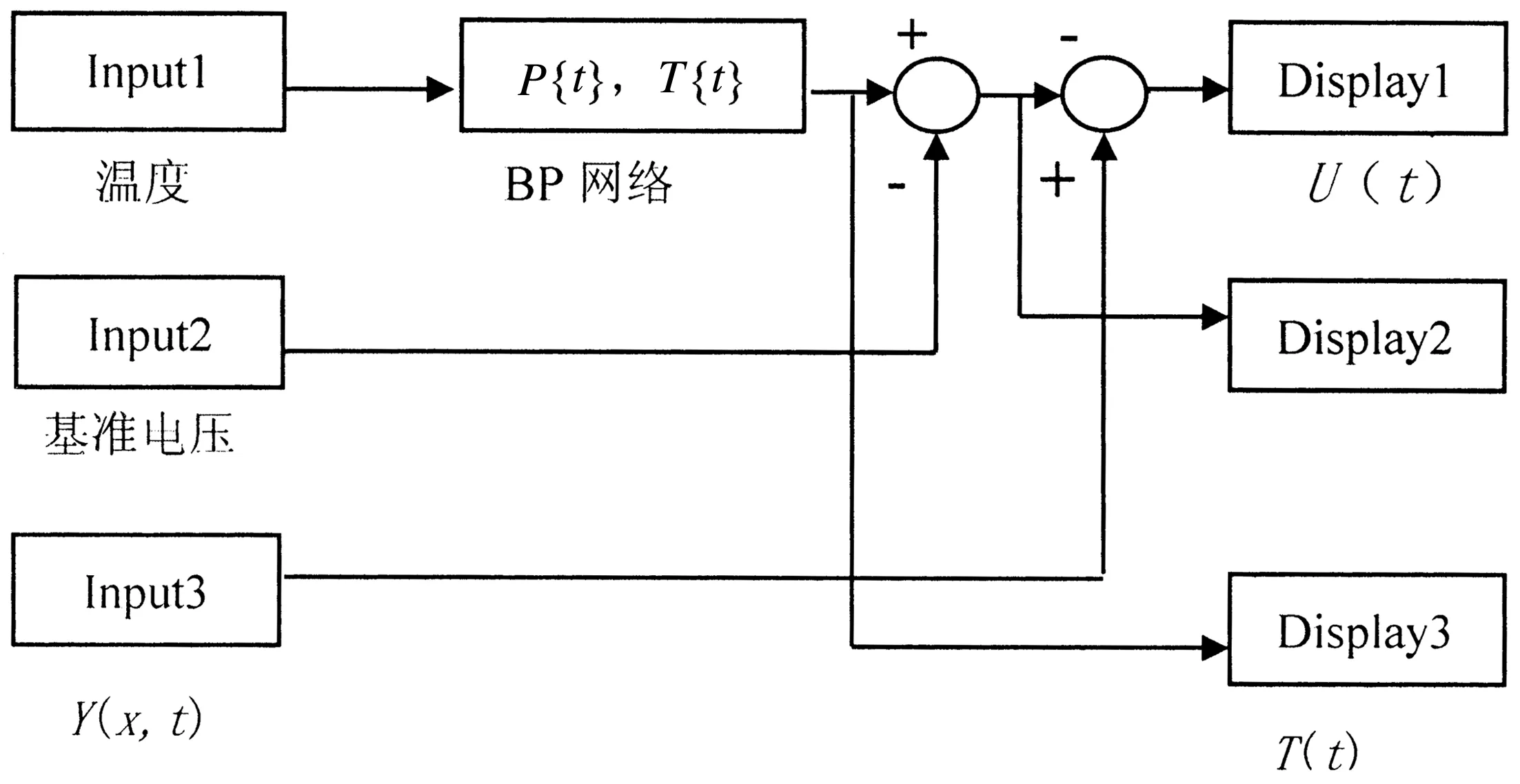
圖5 零位電壓溫度補償模塊框圖

本文中神經網絡模塊為單輸入單輸出系統，則輸入層和輸出層都只具有一個神經元節點。神經網絡模塊選用常見的雙層結構[5]，隱層節點數根據經驗公式n=ni+n0+a=1+1+9=10；其中的n為隱層神經元節點數；ni為輸入層神經元節點數；n0為輸出層神經元節點數；a為[1，10]間的任意常數。

由于二次儀表的溫度特性測試范圍-40℃～80℃，則神經網絡的輸入矩陣PR=[-40，80]。根據常用的方法選擇輸入層到隱層傳遞函數為tansing，隱層到輸出層的傳統函數為purelin，學習函數使用learned，性能函數為mse，學習速率n可取1。利用newff()函數初始化神經網絡模塊的命令為 net=newff([-40，80]，[10 1]，…)。將傳感器溫度特性測量數據分別存入P、T兩個矩陣作為訓練數據[6]，利用MATLAB中的神經網絡訓練函數train()對初始化好的神經網絡模塊進行訓練。train函數將默認使用變梯度反傳算法進行訓練[7]。訓練步數的選擇可由語句net.trainParam.epochs=500定義，該語句定義了一個500步的訓練步數。令訓練后的網絡名稱為net，便可以使用下面的語句對網絡進行訓練：[net，tr]=train(net，P，T，[]，[])。

4 結論

通過仿真可知，補償后的零位電壓值的溫度特性得到較大的改善，如圖6所示。

由圖3與圖6中的數據可計算出，在-40℃～80℃范圍內，零位電壓的溫度誤差由原來的26.83%降低到2.87%。如進行更深入的研究，學習速率能取到小于1的值，適當增加訓練步數，可以進一步提高補償精度。此外，該方法也可應用于其他計量器具的靈敏度溫度特性的補償，為其他計量器具中的電測部分提供一種較好的溫漂補償方法。

圖6 引入BP與神經網絡補償后的零位電壓溫度特性曲線圖

［1］張克.溫度測控技術及應用［M］.北京：中國質檢出版社，2011.

［2］朱家良.溫度顯示儀表及其校準［M］.北京：中國計量出版社，2008.

［3］李鄧化.智能檢測技術及儀表［M］.北京：科學出版社，2012.

［4］張德豐.MATLAB神經網絡編程［M］.北京：化學工業出版社，2011.

［5］張德豐.MATLAB神經網絡應用設計［M］.北京：機械工業出版社，2012.

［6］董志成，任強.基于BP神經網絡的減振器示功圖識別方法［J］.機電工程，2012（08）：929-931.

［7］MATLAB中文論壇.MATLAB神經網絡30個案例分析［M］.北京：北京航空航天大學出版社，2010.