低頻P波荷載下壓電介質中共面裂紋的耦合斷裂行為
張培偉
(東南大學土木工程學院,南京 210096)(東南大學江蘇省工程力學分析重點實驗室,南京 210096)
壓電結構的應用往往與動載荷密切相關,通過交變電流的激勵可以引起此類結構的振動,也可以在受到變形后輸出電信號.因此,一些制造缺陷或在服役中形成的裂紋,常會導致壓電結構精度降低甚至是完全失效.為了保障壓電元器件的可靠性,必須對有缺陷的壓電材料進行深入研究,才能有效評價此類元件的性能.
目前,已有大量關于含缺陷壓電材料的平面問題和反平面問題的研究工作可供參考,但是這些結果對于三維空間問題卻并不完全適用.在空間問題的研究中,可以將裂紋看作是一層空氣或真空薄層,有時假設空洞層為圓形或橢圓形,有時假設薄片為矩形,當空洞層的面積大小相當時,按照矩形假設所計算得到的結果對于工程應用來說一般是偏安全的.Zhang等[1]利用一般Almansi理論研究過矩形裂紋,給出了矩形裂紋的長寬比對壓電材料安全性的影響規律,同時還發現,動荷載與靜荷載作用下裂紋的擴展形式并不相同,在靜載荷下矩形裂紋長邊的中點更容易首先發生擴展,而在動載荷作用下卻并非如此.
為了迎合復雜服役環境的需求,壓電材料的動態斷裂研究尤為重要,因為關于壓電材料靜態斷裂的大量工作對于動態服役的壓電元件的安全評估顯然是不充分的.Zhao和Meguid[2]研究了含有多個共線界面裂紋的壓電層合板的動態斷裂,發現越小的裂紋越容易擴展并最終導致結構破壞.Liu和Zhong[3]研究了2個共線裂紋在面內沖擊荷載作用下的行為,計算結果顯示了電場方向對于裂紋擴展的促進和阻礙規律.
本文采用部分電導通邊界條件,研究了壓電介質中一對共面矩形裂紋的耦合斷裂問題.通過數學建模和變換,將斷裂問題轉化為求解一組對偶積分方程,并經過嚴格的數學推導得到廣義應力場的解析解,進而得到了廣義強度因子和能量釋放率的解析表達式.最后,利用一系列的數值算例,詳細討論了裂紋耦合斷裂的一些規律.
1 模型建立
根據常見壓電結構的工藝和破壞形式,假設壓電材料為均質橫觀各向同性材料,材料的各向同性面平行于x-y平面,2個共面的裂紋位于同一各向同性面內(z=0).采用等面積的矩形擬合裂紋,可以為結構評估提供偏安全的結果,矩形尺寸如圖1所示.常用壓電器件的載荷通常沿著壓電材料的極化方向,即z軸方向,設簡諧應力載荷的形式為σzz(x,y,0)=-σ0eiωτ,其中σ0和ω分別為周期載荷的幅值和圓頻率,τ為時間變量.載荷的激勵源視為無窮遠處,因此可以將載荷引起的應力波近似為平面波處理.
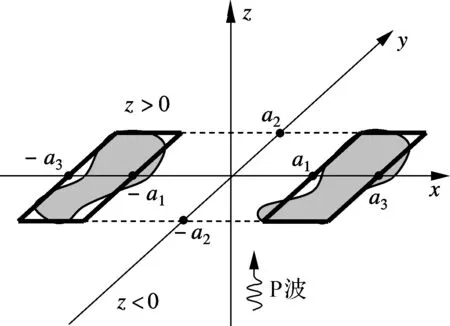
圖1 共面矩形裂紋幾何尺寸
對于遠場為簡諧荷載作用的斷裂問題,根據線彈性疊加理論,可以求解在裂紋上、下表面施加與遠場動載相同頻率和振幅的擾動載荷問題.在理想線彈性體中,包括應力、應變和交變電場等物理量都符合如下的變化規律:
(1)
式中,X可以表示彈性體內位移uk、電勢φ、應力σkl以及電位移Dk(k=x,y,z;l=x,y,z);上角標j=1,2分別表示彈性體位于z=0平面上、下方的物質空間.不計體力和自由電荷,壓電介質的平衡方程和本構方程可以分別表示為
(2)
(3)
(4)
式中,
ρ0,cpq,epq,εpq(p=1,2,3;q=1,2,3)分別表示壓電介質的密度、彈性常數、壓電系數和介電常數.
將本構方程(3)和(4)代入到平衡方程(2),得到位移和電勢表示的壓電介質控制方程為
(5)

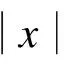
(6)
在裂紋面以外的區域,位移、應力、電位移和電勢滿足連續性條件為
X(1)(x,y,0+)=X(2)(x,y,0-)
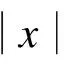
(7)
在距離裂紋區域足夠遠處有
ux(x,y,z)=uy(x,y,z)=uz(x,y,z)=φ(x,y,z)=0
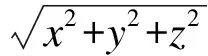
(8)
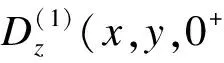
2 邊界值問題的求解
2.1 基本解
壓電介質中的位移可以用位移勢函數Ψ(j)和G(j)表示,即
(9)
將其代入到控制方程(5)可得
(11)
式中,Δ=?,xx+?,yy表示二維拉普拉斯算子.參考文獻[6-7],可以求得位移勢函數、位移分量、電勢、應力分量和電位移分量的表達式為
(12)
(13)
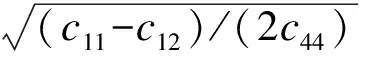
2.2 位移階躍函數
定義裂紋上、下表面之間的位移階躍函數為
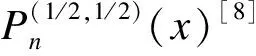
(15)
(16)
(17)
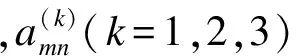
對方程(15)~(17)進行二維傅里葉變換[9],得
(18)
(19)
(20)
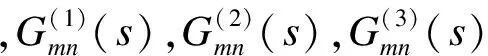
2.3 對偶積分方程的求解
將位移、應力、電勢和電位移的表達式(12)~(13)代入到邊界條件(6)和(7)以及位移階躍函數(14)中,經過傅里葉變換后可得
(21)
(22)
a1≤x≤a3, 0≤y≤a2
(23)
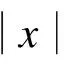
(24)
式中,
[mij]4×4=M-1, [nij]4×4=N-1
將式(18)~(20)代入到方程(23)~(24)中,方程(24)始終自動滿足.對方程(23)關于x在區間[a1,x]上積分并關于y坐標在區間[0,y]上積分,可得
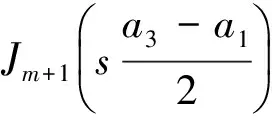
sin(ty)dsdt=-σ0(x-a1)y
a1≤x≤a3, 0≤y≤a2
(25)
[cos(sa1)-cos(sx)]sin(ty)dsdt=0
a1≤x≤a3, 0≤y≤a2
(26)
[sin(sx)-sin(sa1)][1-cos(ty)]dsdt=0
a1≤x≤a3, 0≤y≤a2
(27)
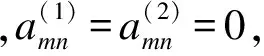
3 斷裂準則
3.1 廣義強度因子
由斷裂力學理論,需求裂紋尖端處廣義應力場.可令式(13)中z=0,即得裂紋尖端場.但當積分變量趨于無窮大時,需要通過如下的關系式來消除積分方程在裂紋邊緣處(x=a1,x=a3,y=a2)的奇異性[8]:
(28)
(29)
考慮到問題的對稱性,下面僅研究x≥0且y≥0區域的情況.經過處理后的裂尖應力和電位移表達式如下:
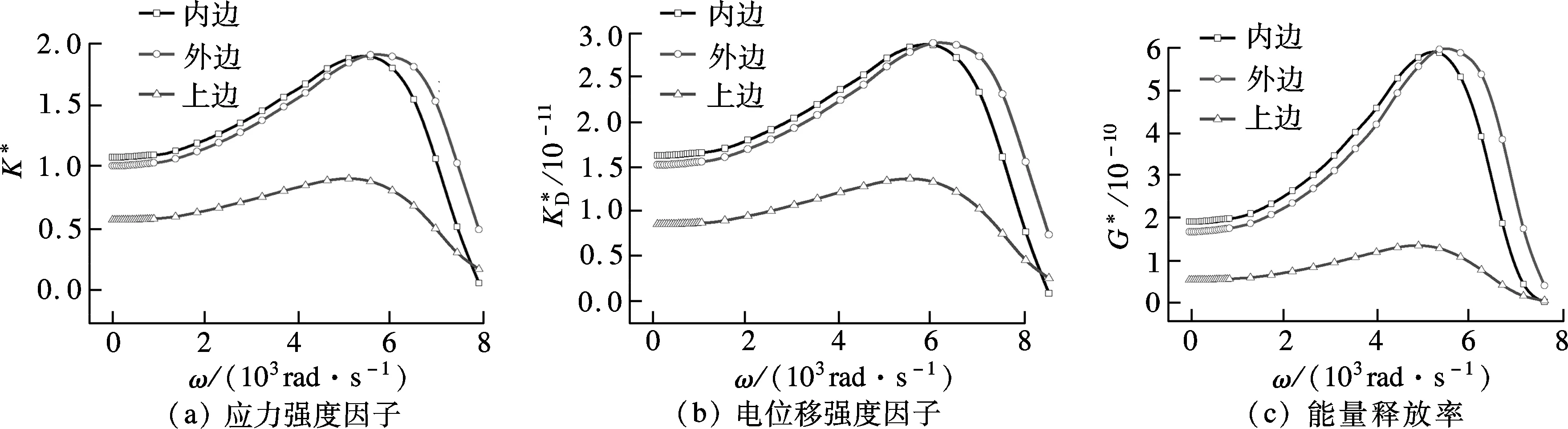
1) 當0≤x (30) 2) 當a2 (31) 利用裂尖應力和電位移場的表達式(30)~(31),可得裂紋前端廣義應力強度因子的表達式如下: 1) 在裂紋的內邊緣處,即x→a1且0≤y (32) (33) 2) 在裂紋的外邊緣處,即x→a3且0≤y 3) 在裂紋的上邊緣處,即y→a2且a1 (36) (37) 利用裂紋閉合能量的概念,以及應力、位移、電位移和電勢的漸進閉合概念,I型裂紋擴展的能量釋放率G的表達式為 Dz(r,0)φz(Δc-r,π)]dr (38) 式中,Δc為裂紋閉合的長度. 裂紋上下表面的位移和裂紋上下表面的電勢分別為 a1 (39) a1 (40) 將裂尖應力表達式(13)、裂紋面位移表達式(39)和裂紋面電勢表達式(40)代入到能量釋放率表達式(38)中,得 (41) 表1 BaTiO3 的相關參數 圖2~圖6給出了裂紋各邊中點處應力強度因子、電位移強度因子和能量釋放率隨載荷圓頻率變化的情況.對比各圖可見,在相同的裂紋幾何尺寸、載荷屬性等條件下,各斷裂準則參數具有相同的變化規律,區別僅是數值大小不同.因此,除了少數幾種特殊情況外,采用這2種斷裂準則判斷的結果具有一致性. 圖2 裂紋各邊中點處斷裂參數隨載荷頻率變化曲線(a2=1.0,a3=1.1,D0/ε0=1.0×108) 圖3 裂紋各邊中點處斷裂參數隨載荷頻率變化曲線(a1=0.3,a2=1.0,a3=1.3,D0/ε0=1.0×108) 圖4 裂紋各邊中點處斷裂參數隨載荷頻率變化曲線(a1=0.5,a2=1.0,a3=1.5,D0/ε0=1.0×108) 圖5 裂紋各邊中點處斷裂參數隨載荷頻率變化曲線(a1=0.1,a2=1.0,a3=0.2,D0/ε0=1.0×108) 圖6 裂紋各邊中點處斷裂參數隨載荷頻率變化曲線(a1=0.1,a2=1.0,a3=0.5,D0/ε0=1.0×108) 在低頻載荷作用下,曲線的第1個極值出現在ω≈6 000 rad/s的附近.這表示當載荷頻率在這附近時,圖2和圖3中所示尺寸的裂紋最有可能發生擴展.圖2和圖3的區別在于,針對2種不同的裂紋尺寸,在不同激勵載荷頻率下,裂紋首先發生起裂的位置有所區別.當2個裂紋之間的距離較近時,裂紋內邊較容易首先發生擴展,也就是說,2個矩形裂紋很可能會擴展并聯通為1個更大的裂紋;當2個裂紋之間的距離較遠時,較高的載荷頻率會引起2個裂紋分別沿裂紋外邊緣擴展,從而形成2個較大的裂紋.對照圖3所示的情況,當ω>6 000 rad/s時裂紋外邊首先擴展.由圖4可知,增大裂紋區域的面積,裂紋外邊的斷裂準則參數持續增大,而裂紋內邊和上邊的斷裂準則參數則逐漸減小,這意味著裂紋更容易向外擴展. 當裂紋沿x軸方向變窄時,圖5和圖6給出了載荷頻率對裂紋擴展行為的影響.裂紋上邊的斷裂準則參數過小,故沒有在圖中出現.該算例所研究的載荷頻率范圍內,曲線并沒有出現極值.為了進一步研究裂紋寬窄對斷裂準則參數的影響,給出了如圖7所示的算例.由圖可知,隨著裂紋寬度的增大,裂紋更容易發生擴展. 圖7 裂紋各邊中點處應力強度因子隨a3的變化曲線(ω=6 000,a1=0.1,a2=1.0,D0/ε0=1.0×108) 圖8為裂紋各邊緣中點處的應力強度因子變化曲線.由圖可知,裂紋外側邊緣的應力強度因子較大,也更容易發生開裂.然而,在進一步更詳細的研究中發現,圖8所表示的結果并不能準確給出裂紋起裂點.圖9給出了圖8算例中裂紋邊上各點的應力強度因子,可以明顯看出,斷裂準則參數最大值并非出現在裂紋邊緣的中點處,因此不能僅根據裂紋中點處的應力強度因子來判斷裂紋的起裂情況.為了準確評估裂紋的擴展行為,將各頻率下裂紋邊上應力強度因子的最大值提取出來,并繪于圖10中.由圖10可知,隨著裂紋寬度的增加,裂紋上邊緣發生擴展的可能性逐漸變大. 圖8 裂紋各邊中點處應力強度因子隨載荷頻率變化曲線(a1=0.1,a2=1.0,a3=2.1,D0/ε0=1.0×108) 圖9 裂紋各邊應力強度因子分布情況 (ω=2 000,a1=0.1,a2=1.0,a3=2.1,D0/ε0=1.0×108) 圖10 裂紋各邊最大應力強度因子隨載荷頻率變化曲線(a1=0.1,a2=1.0,a3=2.1,D0/ε0=1.0×108) 通過對壓電介質中2個共面裂紋耦合斷裂問題的研究,考慮裂紋的部分電導通特性,得到了載荷頻率和裂紋寬度對裂紋擴展的影響規律.與靜載荷作用下的裂紋擴展估計不同,僅采用裂紋邊上中點處的應力強度因子或能量釋放率并不能完全準確地預測裂紋行為,必須對裂紋邊上各點的應力強度因子進行計算,才能給出正確的結論. ) [1] Zhang P W, Wu H P, Wang B. Time-harmonic P-waves engulfing a rectangular limited-permeable crack in piezoelectric medium: energy density and energy release [J].TheoreticalandAppliedFractureMechanics, 2011,59(3): 169-184. [2] Zhao X H, Meguid S A. On the dynamic behaviour of a piezoelectric laminate with multiple interfacial collinear cracks [J].InternationalJournalofSolidsandStructures, 2002,39(9): 2477-2494. [3] Liu F, Zhong X C. Transient response of two collinear dielectric cracks in a piezoelectric solid under inplane impacts [J].AppliedMathematicsandComputation, 2010,217(8): 3779-3791. [4] Hao T H, Shen Z Y. A new electric boundary-condition of electric fracture-mechanics and its applications [J].EngineeringFractureMechanics, 1994,47(6): 793-802. [5] Hao T H. Multiple collinear cracks in a piezoelectric material [J].InternationalJournalofSolidsandStructures, 2001,38(50/51): 9201-9208. [6] Ding H J, Chen B, Liang J. General solutions for coupled equations for piezoelectric media [J].InternationalJournalofSolidsandStructures, 1996,33(16): 2283-2298. [7] Yang F Q. Fracture mechanics for a Mode Ⅰ crack in piezoelectric materials [J].InternationalJournalofSolidsandStructures, 2001,38(21): 3813-3830. [8] Gradshteyn I S, Ryzhik I M.Tableofintegral,seriesandproducts[M]. New York: Academic Press, 1980. [9] Erdelyi A.TablesofIntegralTransforms[M]. New York: McGraw-Hill, 1954. [10] Morse P M, Feshbach H.MethodsofTheoreticalPhysics[M]. New York: McGraw-Hill, 1958. [11] Itou S. 3-Dimensional wave-propagation in a cracked elastic solid [J].JournalofAppliedMechanics,ASME, 1978,45(4): 807-811. [12] Zhang P W, Zhou Z G, Wu L Z. Coupled field state around three parallel non-symmetric cracks in a piezoelectric/piezomagnetic material plane [J].ArchiveofAppliedMechanics, 2009,79(10): 965-979. [13] Zhang P W, Zhou Z G, Li G. Q. Interaction of four parallel non-symmetric permeable mode-Ⅲ cracks with different lengths in a functionally graded piezoelectric material plane [J].ZeitschriftfürAngewandteMathematikundMechanik, 2009,89(9): 767-788. (in Russian) [14] Itou S. Three-dimensional dynamic stress intensity factors around two parallel square cracks in an infinite elastic medium subjected to a time-harmonic stress wave [J].ActaMechanica, 2000,143(1/2): 79-90. [15] Itou S. 3D dynamic stress intensity factors at three rectangular cracks in an infinite elastic medium subjected to a time-harmonic stress wave [J].ArchiveofAppliedMechanics, 1999,69(4): 286-298.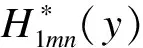
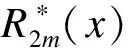
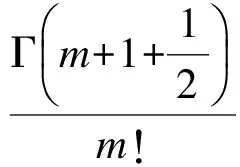
3.2 能量釋放率
4 數值計算結果及討論





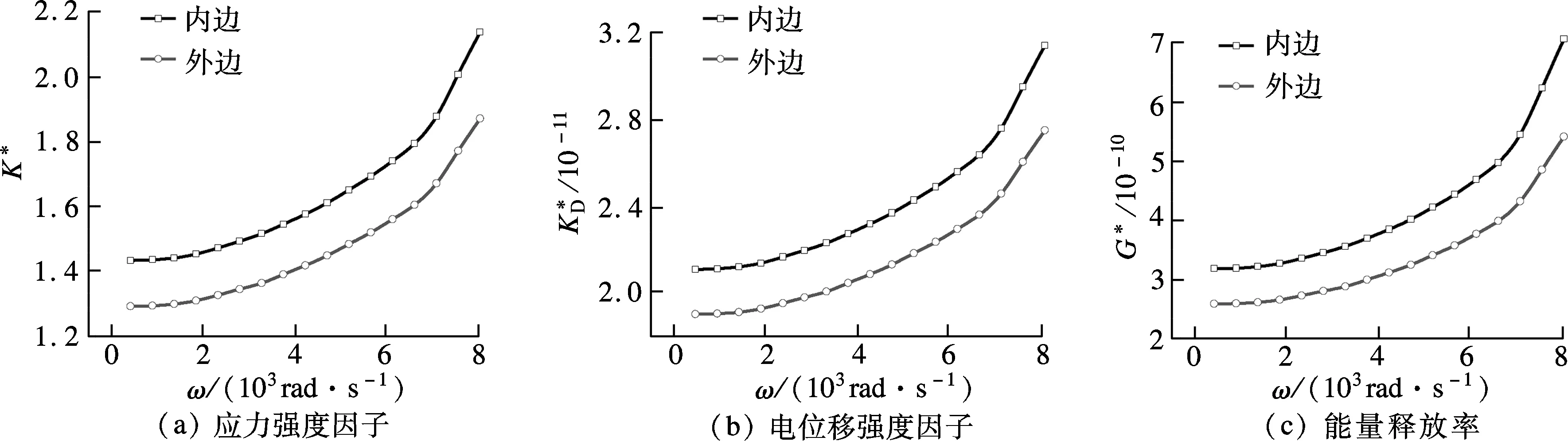
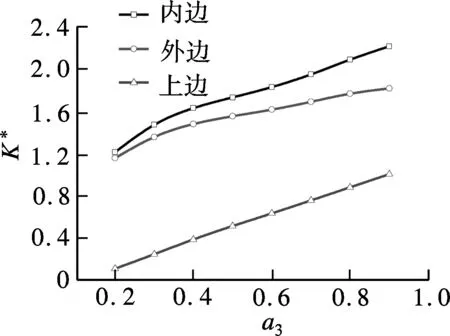

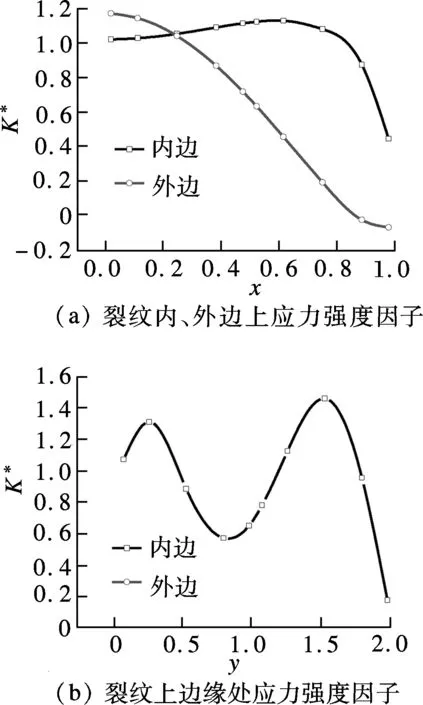
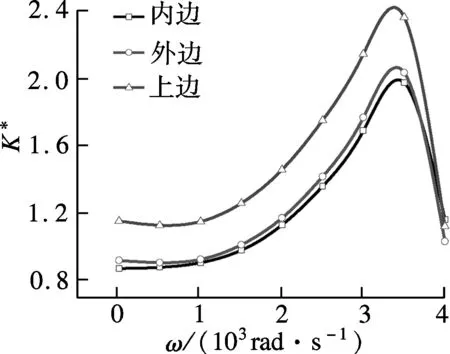
5 結語

