DCS模擬量數據的分部壓縮方法

李 煥，劉海濤

(1.應天職業技術學院機電工程系，江蘇南京210046；2.南京工程學院電力工程系，江蘇南京,210067；)

0 引言

與DCS接口中，串行通訊是常見的接口方式。為了提高通訊效率，需要對通訊的數據進行壓縮處理。

DCS模擬量的壓縮方法中，常用整數表示工程量，即將模擬量的按其量程線性化處理為兩字節正整數（0～65535），應用時再轉換為工程量。這種方法由于要維護模擬量的量程表，不便于通信；另一類常用的壓縮方法是采用LZW等基于字典模型的壓縮算法。模擬量數據是以單精度浮點數存放的，數據的冗余度很小，傳統的壓縮處理方法的壓縮效果都不理想。

本文從模擬量在計算機中的表示方法入手，首先將模擬量預處理，再針對數據的不同部分采用不同的方法進行壓縮，最后將壓縮后數據組合起來。這樣既充分考慮到了數據的特點，又充分利用了壓縮方法的適應性。

1 模擬量的表示方法及特點

1.1 模擬量的表示方法

DCS模擬量用單精度浮點數表示，占用4個字節，可以精確到7位有效數字。按文獻[3]標準（以下簡稱標準）表示。設一個浮點數R，可使用三元組｛S，E，M｝來表示：S為符號位，用1位表示。S＝0表示R為正數，S＝1表示R為負數；E為指數，用8bits表示。實際指數要經E－127計算后得到；M為尾數，用23bits表示。浮點數R為S×1.M E（1為隱含的一位尾數，不在M中表示）。

1.2 模擬量的特點

數據壓縮需要信息有足夠的冗余度。以標準表示的模擬量不利于壓縮。即便差值很小的數據，在計算機中表示結果差別很大，如1234.5在計算機中用四字節表示為：68 154 80 0 ，而1234.6表示為：68 154 83 51，僅有符號位和指數位表示相同，尾數完全不同，這樣就造成了壓縮的難度。

現以200個模擬量數據為樣本分析其特點。樣本數據隨機產生，其范圍為[0.0，1000.0]。按照標準存儲的數據從字符概率分布較平均，若用通用數據壓縮方法壓縮這些數據，得不到很好的效果。

雖然浮點數的信息冗余度很小，但若用其表示DCS模擬量，仍有以下特點：

（1）各工程量數值多數大于零，因此標準表示中，符號位S大多為零；

（2）各工程量的量程相差約為0.0001～10000倍，因此標準表示中，指數差值約為-4～4；

（3）從數據精度考慮，工程量一般保留5位有效數字即可。因此標準表示中，尾數部分有可壓縮的信息。

2 模擬量的預處理

模擬量預處理的目的是為了產生更多的冗余信息，獲得更好的壓縮效果。通信時一般將模擬量按測點表以自然順序排列。根據1.2節的分析可知，若將模擬量按其三元組順序排列，即：N個模擬量數據，其自然排列順序為｛S1，E1，M1｝、｛S2，E2，M2｝、…、｛SN，EN，MN｝，共占用4N字節。壓縮前將模擬量序列按字節重新排列為：S1S2…SNE1E2…ENM1M2…MN。因符號位S為1位，重新排列后將8個模擬量的符號位合并為1字節。故重新排列后N個模擬量共占用字節數為4N+N/8(+1)字節。（括號中+1字節表示N不是8的整數倍時總字節數+1）。

圖1(a)為樣本數據經重新排列后字節分布情況。可以看出數據已呈現明顯的規律性：第一部分數據[1，25]為數據的符號，是樣本數據的符號。樣本數據均為正，因此由符號位構成的這部分數據全為零；第二部分數據[26，225]為N個樣本數據的指數，根據1.2節分析可知，各數據的指數差值大約在-4～4之間，故有較大的壓縮空間；最后一部分數據[226，825]為N個樣本的尾數，呈隨機分布。

第一次預處理是數據無損的。考慮到DCS模擬量精度要求有5位有效數字即可。根據信息理論，1位十進制數可以精確表示log210≈3.32位二進制數。單精度浮點數表示模擬量時，4位二進制約可表示1位十進制。因此，在精度滿足DCS系統要求的情況下，可以減少一個字節尾數。第二次預處理將尾數的最低字節置零，進一步提高數據的冗余信息。圖1(b)為第二次預處理后的字節分布情況。可以看出，相比第一次預處理，數據最后一部分[626，825]全為零，可以更好地被壓縮。

3 壓縮算法的選擇

3.1 壓縮算法選擇原則

壓縮算法要根據原始數據的特點以及對速度、性能的綜合要求來選擇。模擬量的壓縮應用在數據通信中，對速度的要求較高。因此壓縮算法不能過于復雜，運算量要小。

從預處理后的樣本數據可以看出，每一部分數據的特點不同，因此選擇壓縮算法時應針對不同特點的數據采用不同的壓縮算法來處理。第一部分數據（由符號位組成）為零（或絕大部分為零），可以采用游程編碼（Run Length Encoding）；第二部分數據（由指數組成）數值間相差不大，可用差分編碼（Differential Encoding）；第三部分數據（由部分尾數組成）隨機性較大，壓縮效果不明顯，因此不進行壓縮；第四部分數據（由最低字節尾數組成）均為零，可采用游程編碼。

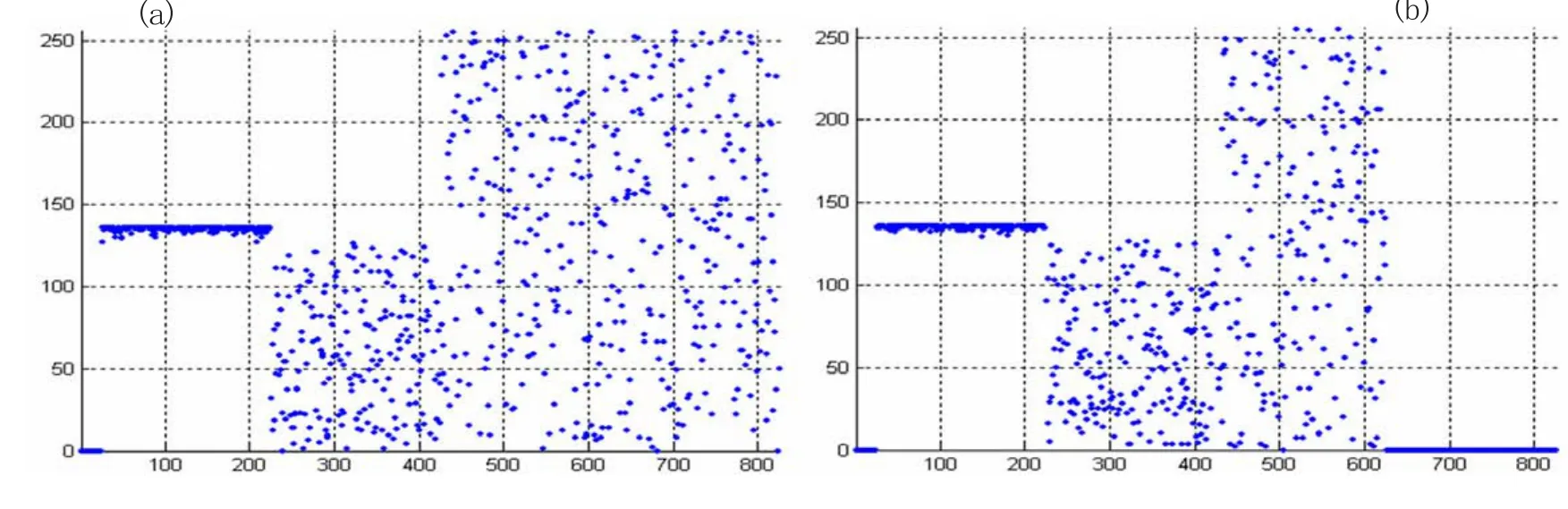
圖1 預處理后字節分布Figure 1 The Bytes Distribution of Preprocessing

3.2 差分編碼

差分編碼又稱相關編碼。當源數據之間差值不大時，用數據間的差值代替源數據序列。較小的差值可以用較少的位數表示。本文用4位二進制表示一個差值。

源數據中序列E1E2…EN為數據的指數，其差值約在-4～4之間，用4位二進制表示此差值：最高位用來表示差值的符號，其余三位表示差值，-7保留。可表示的差值范圍為-6～+7；若差值大于此范圍，則不壓縮，用原碼輸出。為了區分是差值輸出還是原碼輸出，用保留的-7表示下一字節為原碼輸出。N字節源序列，若每一字節都可以用相鄰差值來表示，其理想壓縮比為1:(N/2+1)/ N=1:0.5+1/N。

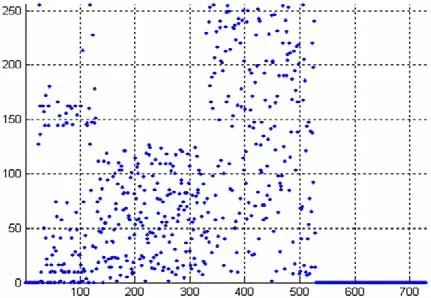
圖2 差分編碼后字節分布Figure 2 The Bytes Distribution After Differential Encoding

圖2為樣本數據差分編碼壓縮后字節分布。可以看到，源數據中表示指數的部分已經被有效壓縮。樣本數據由825字節壓縮到726字節，實際壓縮率為88.0%。

3.3 游程編碼

游程編碼的思路是：若數據項d在源數據中連續出現n次（n稱為重復因子），則在輸出流中以nd代替n個重復項d。游程編碼也可能出現壓縮比大于1的情況。為了區分輸出項是重復因子還是被壓縮數據，規定當重復因子n≥3時，輸出ddd(n-3)；n＜3時，輸出n個d，即不壓縮輸出。另外重復因子3≤n≤255，若數據項d重復次數大于255，則要重新進行游程編碼。設源數據長度為N，包含M次重復，每次重復平均長度L，則游程編碼壓縮比為1:(N-M×(L-4))/N。

樣本數據經預處理后第一部分（由符號位組成）和第四部分（由最低位尾數組成）可以用游程編碼。這部分數據可以獲得很高的壓縮比。第一部分理想壓縮比為1:4/25=1:0.16；第四部分理想壓縮比為1:4/200=1:0.015。

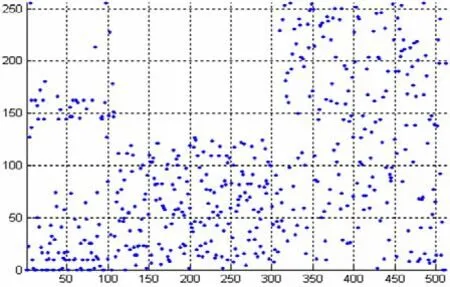
圖3 游程編碼后字節分布Figure 3 The Bytes Distribution After RLE

圖3為經游程編碼壓縮后的數據分布圖。由上一級差分編碼壓縮后的726字節壓縮至510字節，實際壓縮比為1:0.70。

4 結論

200個樣本數據經預處理，對一部分數據進行差分編碼、對另一部分數據進行游程編碼，最終有510個字節。因此綜合壓縮比為1:510/800≈1:0.64，節省約36%的空間。由于樣本數據的隨機性，因此可以推廣到一般情況。得到以下結論：

（1）分部壓縮方法可以獲得約1:0.64的壓縮比；

（2）分部壓縮方法為二級壓縮算法構成。分別針對模擬量中不同信息類型的數據進行分部壓縮；

（3）差分編碼和游程編碼的算法的復雜度低，其時間復雜度和空間復雜度均為O(n)，故算法效率很高。

（4）壓縮過程未涉及到數據的工程特性，因此算法可推廣至工業過程控制領域，具有一定的實用價值。

[1] 徐慧.實時數據庫中數據壓縮算法的研究[D].浙江：浙江大學信息學院，2006

[2] 拓廣忠，慕群.實時數據庫原理及其壓縮技術分析[J].華北電力技術.2004（6）：17-20

[3] 中國電子技術標準化研究所，GB/T 17966－2000 微處理器系統的二進制浮點運算[S].北京：中國標準出版社，2000

[4] David Salomon，數據壓縮原理與應用（第二版）[M].吳樂南，譯.北京：電子工業出版社，2003