關于自然光在兩種介質分界面上反射和折射時的偏振特性討論

郭中華

（蘭州城市學院培黎工程技術學院，甘肅 蘭州 730070）

在一些基礎光學教材［1，2］中，討論光在兩種介質分界面上發生反射、折射現象時光的偏振態變化規律時，主要側重于利用菲涅爾公式分析光矢量振幅的變化規律，對于反射光和折射光的偏振度，只作簡單的介紹.文獻［3］中利用入射、折射時的光強關系，詳細討論了自然光在介質分界面上折射時的偏振度，并建立了實驗系統進行驗證，實驗表明，折射光偏振度隨入射角的增大而單調增加，布儒斯特角對其沒有影響，并不像基礎光學教材中認為的那樣.另有文獻［4］定量分析了反射光和折射光偏振度與布儒斯特角的關系，以n＝1.56的玻璃介質為例，得到與文獻［3］不同的結果，肯定了有關教科書的結論.本文從理論上詳細分析了自然光在分界面上反射光和折射光的偏振特性，并進一步探討了偏振度變化的規律及與介質折射率、光強反射率、透射率和介質層數的關系.

1 反射光和折射光的偏振度

設折射率為n2的均勻介質Ⅱ處于折射率為n1的介質Ⅰ中，自然光以入射角i1入射到上表面，發生兩次反、折射從下表面出射，取N（＝1）為介質層數.在介質上表面發生反、折射時，入射光、反射光和折射光振幅中各分量的比例關系可由菲涅爾公式［5］給出

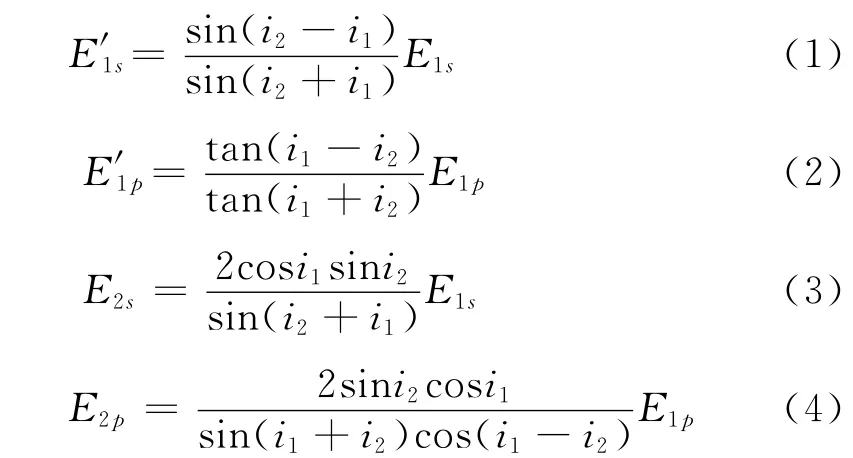
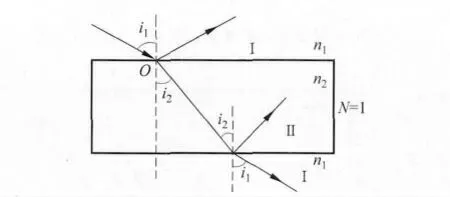
圖1 自然光在介質分界面上的反射、折射情況

為了得到反射光和折射光的偏振度，根據不同介質中光強的定義

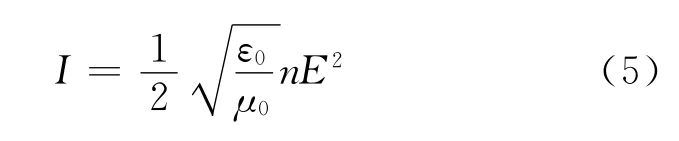
則相應入射光的光強為

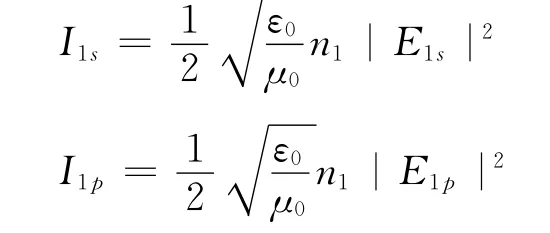
反射光的光強為

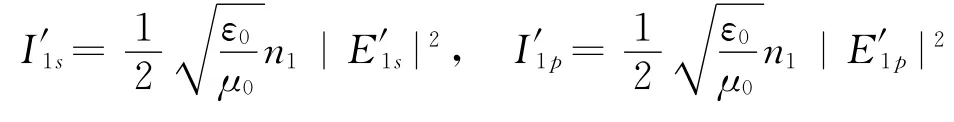
入射光為自然光，有｜E1s｜＝｜E1p｜，由于入射光和反射光在同種介質中，因此光強反射率為

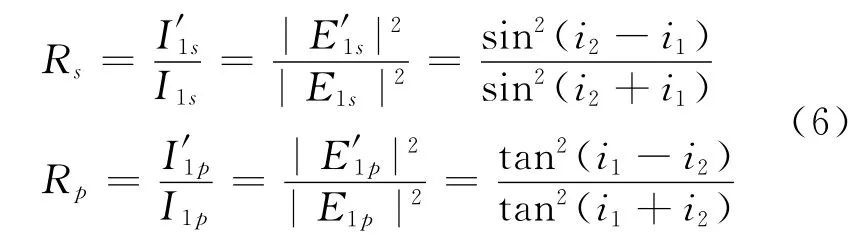
根據偏振度的定義［1］，則反射光的偏振度為

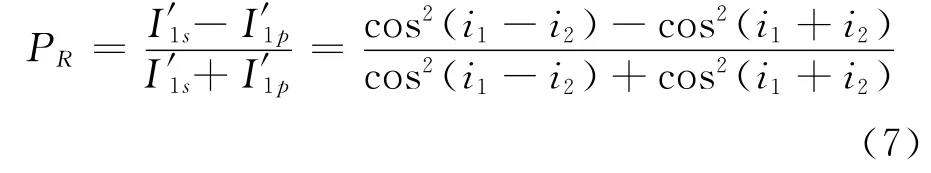
同理可知折射光的光強為

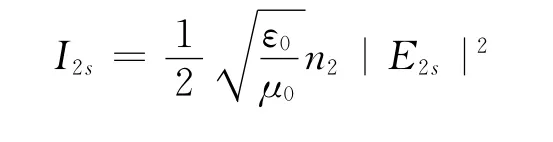
折射光和入射光在不同介質中，因此光強透射率為

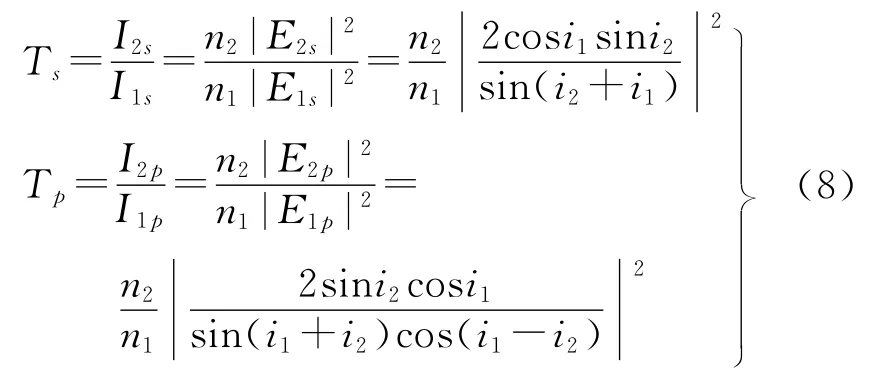
可知折射光的偏振度為

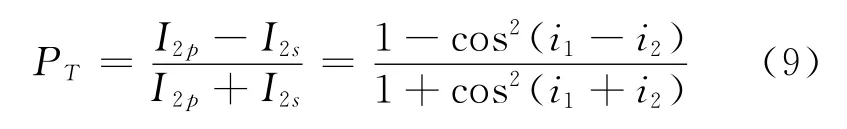
當自然光以任意入射角i1入射，由式（7）和式（9）可知0＜P＜1，反射光和折射光均為部分偏振光.

2 反射光和折射光偏振度的變化規律

2.1 不同介質分界面處反射光和折射光偏振度隨入射角的變化

如圖1情形，首先考慮自然光在介質上表面反射、折射時的偏振度變化規律.為了討論簡便，取介質Ⅰ為空氣，介質Ⅱ為玻璃，折射率n2范圍在1.5～1.8，根據式（7）結果，可得到在不同入射角下反射光偏振度隨折射率的變化曲線（圖2）及隨入射角的變化曲線（圖3）.可以看到，不同介質表面反射光的偏振度變化特征類似，先隨入射角的增大而增加，取得極值（PR＝1）后隨入射角的增大而減小，隨著介質折射率的增加，偏振度極值位置向角度增大的方向移動.

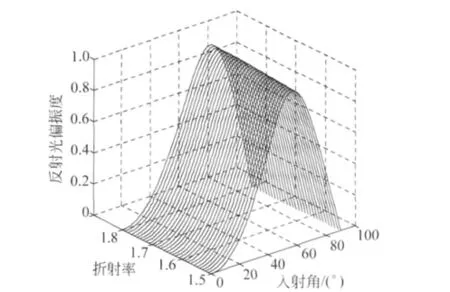
圖2 不同入射角下反射光偏振度隨折射率的變化

根據式（6）可得到光強反射率隨入射角的變化曲線（圖4），可以看出反射光中s分量的相對強度隨入射角單調增加，而p 分量的相對強度先隨入射角減小，因此反射光偏振度在這一過程中逐漸增大，隨著p 分量的相對強度在布儒斯特角（i0＝arctan（n2/n1））處降為零，此時反射光中只有s分量，從而偏振度最高，而后隨著入射角的增加p 分量的強度迅速增大，所以反射光偏振度又逐漸減小.

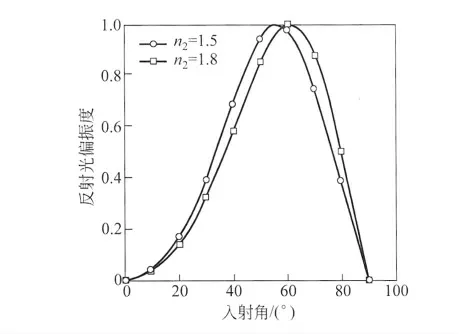
圖3 反射光偏振度隨入射角的變化

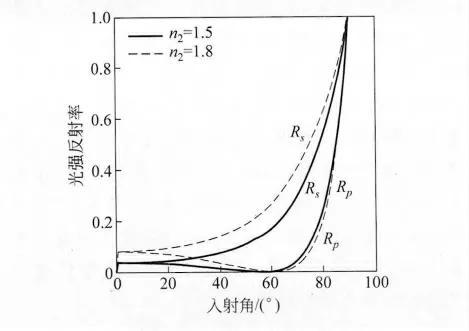
圖4 光強反射率隨入射角的變化

對于折射光而言，由式（9）結果，亦可得到在不同入射角下折射光偏振度隨折射率的變化曲線（圖5）及隨入射角的變化曲線（圖6）.

可以看出，在介質折射率n2＝1.5～1.8范圍內，折射光偏振度的變化特征是類似的，均隨著入射角的增大而單調增加，沒有特例，這與文獻［3］的結果是一致的，并不像基礎光學教材中所描述“以布儒斯特角入射時，折射光的偏振度最高”［1，2］.

根據式（8）可得到光強透射率隨入射角的變化曲線（圖7），可以看出，s分量和p 分量相對強度均是隨著入射角單調減小的，盡管在布儒斯特角處p 分量100%透射，透射光能流在此處取得最大值，但對于偏振度定義公式（9）來說相對強度的比例關系使得偏振度的變化不受這一特殊角度的影響.

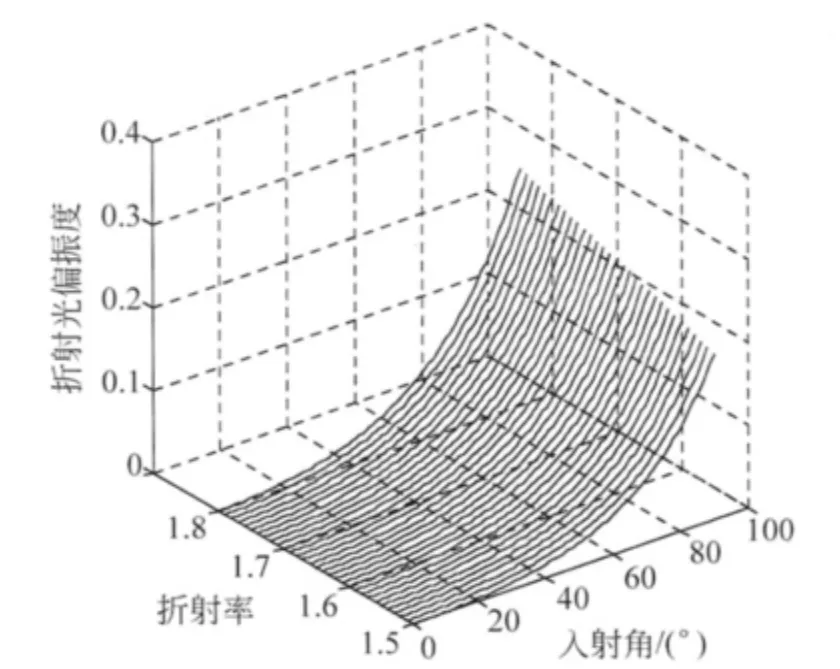
圖5 不同入射角時折射光偏振度隨折射率的變化

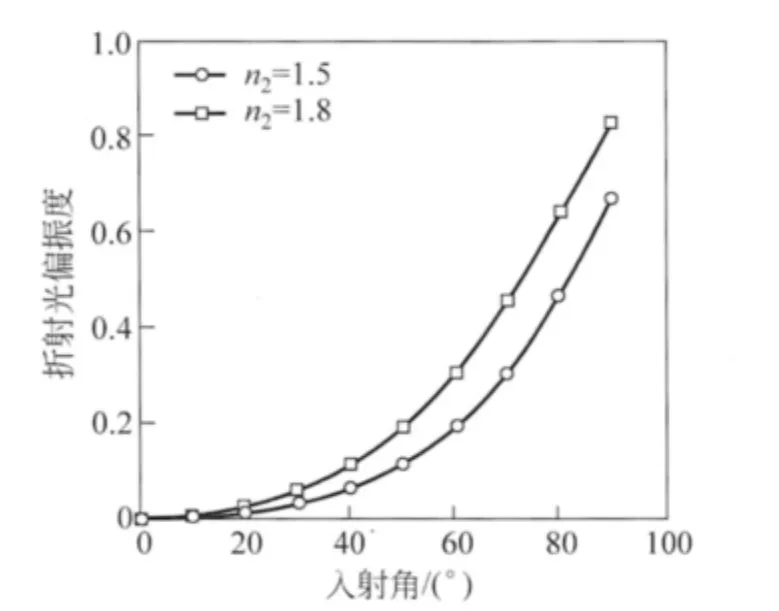
圖6 折射光偏振度隨入射角的變化

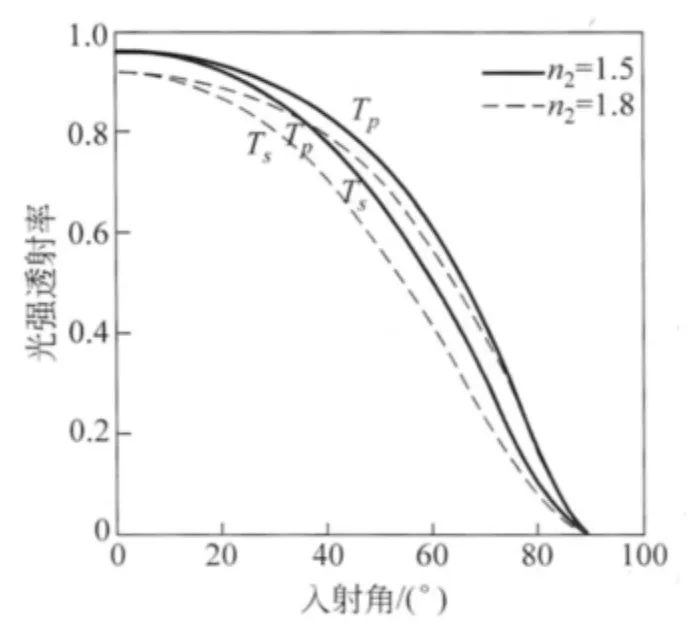
圖7 光強透射率隨入射角的變化

2.2 透射光偏振度隨介質層數的變化

在圖1情形中，當折射光經介質下表面透射出時，由式（3）和式（4）的結果可知透射光各分量振幅關系為

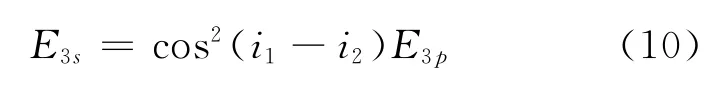
因此透射光的偏振度為

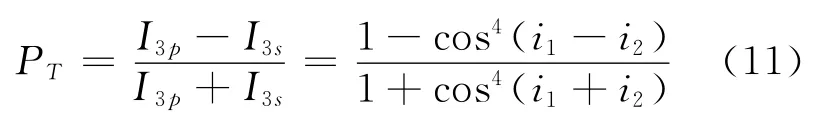
由此可得到經過單層介質透射后，不同入射角下透射光偏振度隨折射率的變化曲線（圖8）及隨入射角的變化曲線（圖9），所得結果和圖5中類似，不同介質材料的透射光偏振度均隨入射角增加而單調增大，沒有特例，經過單層介質后，透射光的偏振度數值均明顯增大.

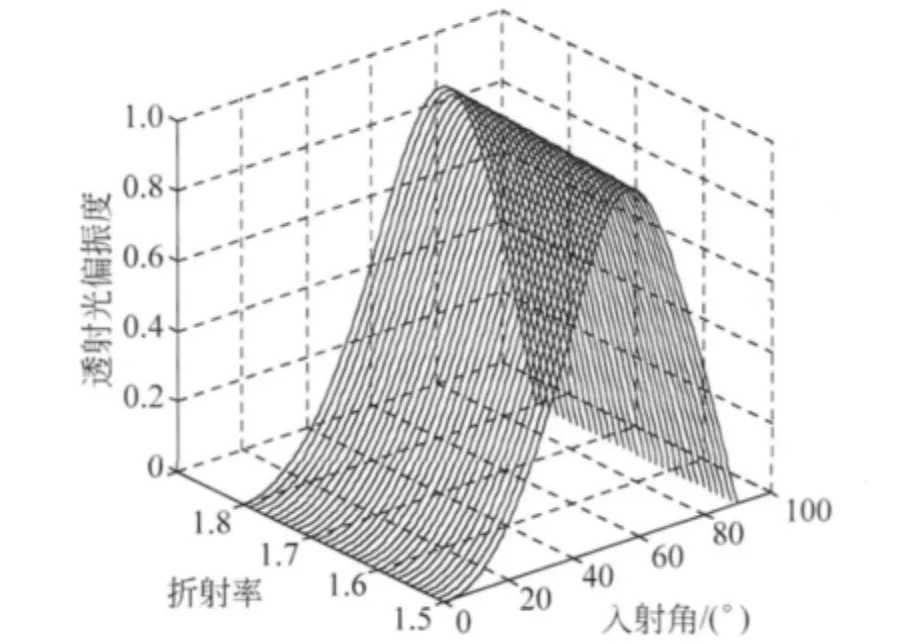
圖8 N=1時不同入射角下透射光偏振度隨折射率的變化

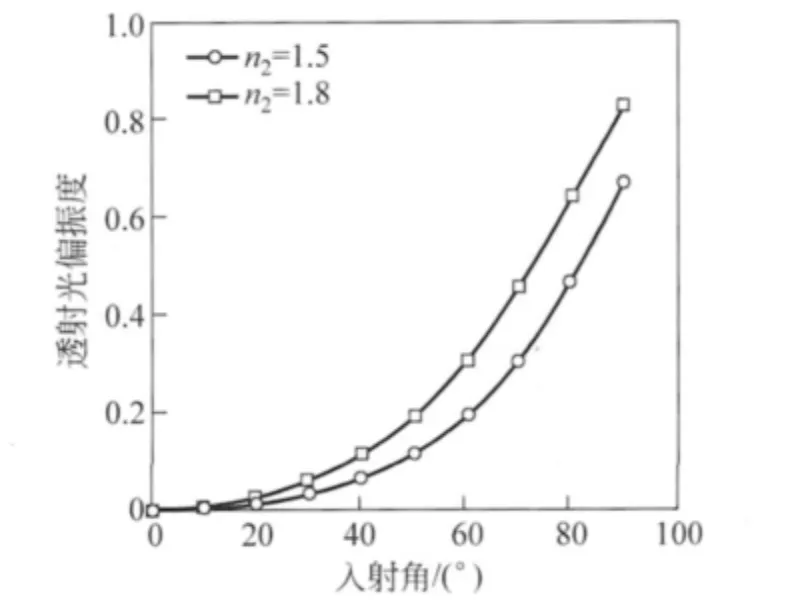
圖9 N=1時透射光偏振度隨入射角的變化

從式（11）可推知經由N 層平行介質層后，透射光的偏振度為

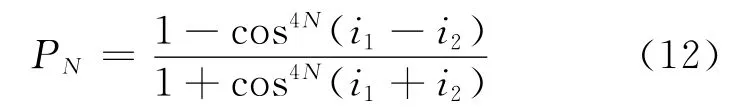
介質層數目對偏振度的影響如圖10所示，隨著介質層數目的增多，透射光的偏振化程度明顯加快，在小角度情況下迅速達到1變成全偏振光.

3 結論

本文詳細分析了自然光從空氣到各種玻璃介質反射光和折射光的偏振特性，分析結果具有一般性，結果表明：

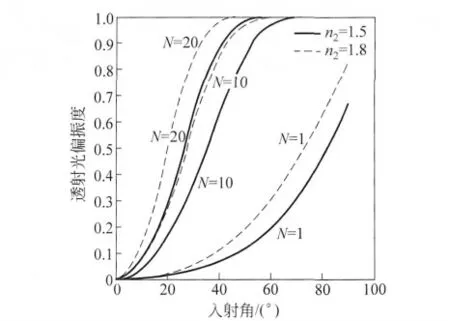
圖10 透射光偏振度隨介質層數的變化

（1）當自然光入射角0＜i1＜i0時，反射光偏振度隨入射角單調增大，在相同入射角情形下，折射率越大的介質表面，反射光偏振度越小；在i1＝i0時反射光偏振化程度最大PR＝1，反射光為全偏振光；當i0＜i1＜90°時，反射光偏振度又隨入射角增大而單調變小，相同入射角情形下，折射率越大的介質表面，反射光偏振度越大.

（2）不同介質材料透射光的偏振度變化規律類似，均隨入射角的增大而單調增大，與是否以布儒斯特角入射無關，在折射率范圍n2＝1.5～1.8內沒有特例，在相同入射角情形下，折射率越大的介質材料其透射光偏振度也越大.

（3）介質層數目越多，相同入射角下透射光偏振度越大，對折射率n2＝1.5的介質，介質層數目在17層透射光可變為全偏振光，而對折射率n2＝1.8的介質，介質層數目在10層透射光就變為全偏振光.

［1］姚啟鈞.光學教程［M］.4版.北京：高等教育出版社，2008：215－222.

［2］廖延彪.偏振光學［M］.北京：科學出版社，2003：28－30.

［3］王靜，宋連科，劉云安，等.自然光在多層介質分界面上折射時的偏振度［J］.大學物理，2006，25（4）：36－38.

［4］高潤梅.自然光在兩種介質表面發生反射和折射時的偏振特性［J］.蘭州大學學報：自然科學版，2008.44（專輯）：292－294.

［5］趙凱華，鐘錫華.光學［M］.北京：北京大學出版社，1984：245－260.