水下爆炸爆源定位方法與誤差分析＊

龍仁榮，付躍升，張慶明

（1.北京理工大學爆炸科學與技術國家重點實驗室，北京100081；2.福州大學紫金礦業學院，福建 福州350108）

水下爆炸實驗中，由于暗流與海浪的作用，藥包難以一直停留在一個固定的位置；在魚雷爆炸實驗時，由于魚雷在運動中爆炸，爆炸時的準確位置更加難以預知。為了準確確定實驗原始條件，精確評估實船抗爆性及魚雷的爆炸威力，必須在起爆后根據傳感器測量信號對爆源進行精確定位。

目前，水下爆炸實驗中爆源定位方法有GPS RTK 技術［1－5］、沖擊波零時法［6］等，這些方法都存在系統復雜、計算精度不高的問題。

本文中，擬采用最小誤差逼近法解決這一問題，這一方法具有系統簡單、定位誤差小的優點。

1 計算原理

1.1 計算流程

最小誤差逼近法要求至少布置4個水中自由場壓力測點及配套測量系統，通過爆炸后已知位置的測點測到的自由場壓力時程曲線和輸入藥量、水的聲速等原始條件進行計算，計算流程如圖1所示。

圖1 計算流程示意圖Fig.1 Computation flow process chart

1.2 假定爆源處起爆后各參量的計算

1.2.1 水中沖擊波傳播時間的計算

水中爆炸后，沖擊波至各測點的傳播時間與傳播路徑長度、路徑上各處壓力以及水的聲速等各因素有關。沖擊波沿傳播路徑上各點的波速與該點處壓力密切相關，對于測點距爆源較近的情況，二者的關系對精確求解爆源位置至關重要。鑒于水的高壓狀態方程的復雜性，并便于實際工程的準確計算，本文中將水中沖擊波傳播速度寫為下列形式

式中：ci為爆源至測點i間的沖擊波平均傳播速度；c0為水的當地聲速；k 為壓力修正系數，此系數是與對應測點處自由場超壓p 相關的量，可寫為

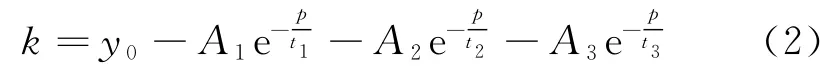
式中：y0、A1、A2、A3、t1、t2、t3為待定系數，可由實驗確定。本文中測到的壓力修正系數隨測點處的壓力變化曲線如圖2 所示，實測條件為海水中200g裸裝TNT 爆炸。

根據假定的爆源及實際測點位置，則沖擊波從假定爆源到第i個實際測點傳播時間的計算值tc，i為

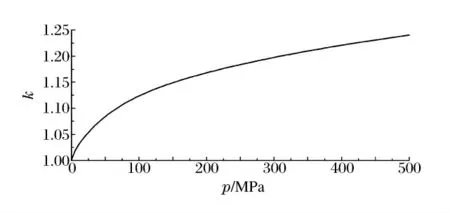
圖2 壓力修正系數隨測點處壓力變化曲線Fig.2 Pressure modifying factor as a function of pressure at observation point

式中：Li為假定爆源到測點i之間的距離。自第2個測點開始，各測點與距實際爆源最近處測點（實測中最早起跳的測點）的傳播時間差Δtc，i為

1.2.2 測點處自由場壓力峰值的計算

水中沖擊沖擊波壓力峰值可以通過數值計算求得［7］，也可以通過經驗公式求得。大量實驗證明，庫爾公式在水中爆炸自由場壓力峰值計算中具有較高的可信度，本文中采用此公式，即

1.2.3 計算值與實測值之差的均方根的計算

沖擊波傳播時間差計算值與實測值之差的均方根σΔt為

式中：Δtf，i為由實測數據得到的各測點與距實際爆源最近處測點的傳播時間差，n 為測點總數量。

所有測點自由場壓力峰值計算值與實測值之差的均方根σp為

式中：pf，i 為由實測數據得到的各測點自由場壓力峰值。

考慮到σΔt和σp的權重相同，計算用的均方根為合計均方根σ，

實際計算中，每劃分一次網格，就假設爆源在每個網格節點上，對逐個節點進行計算，合計均方根最小值對應的節點處即為本一輪計算確定的爆源位置。

2 計算結果

根據本方法編制了計算機程序，并應用于實際實驗中。在眾多應用實例中，現列出一個具有代表性的計算結果。實驗時，將藥包及傳感器全部固定在一個剛性架子上，使它們之間的相對位置不動，采用的TNT 藥包質量為40g，密度1.55g／cm3，海水聲速1 521m／s，爆源實際位置為（0.500m，0.500m，－0.470 m），測點坐標、所測沖擊波傳播時間tf，i、所測壓力峰值pf，i及測點與爆源距離計算誤差ε如表1 所示。計算得到的爆源位置為（0.500m，0.519m，－0.458m），測 點 布 置與計算爆源位置見圖3，爆源至測點距離誤差絕對值的平均值為1.597 0%，完全滿足工程應用的要求。

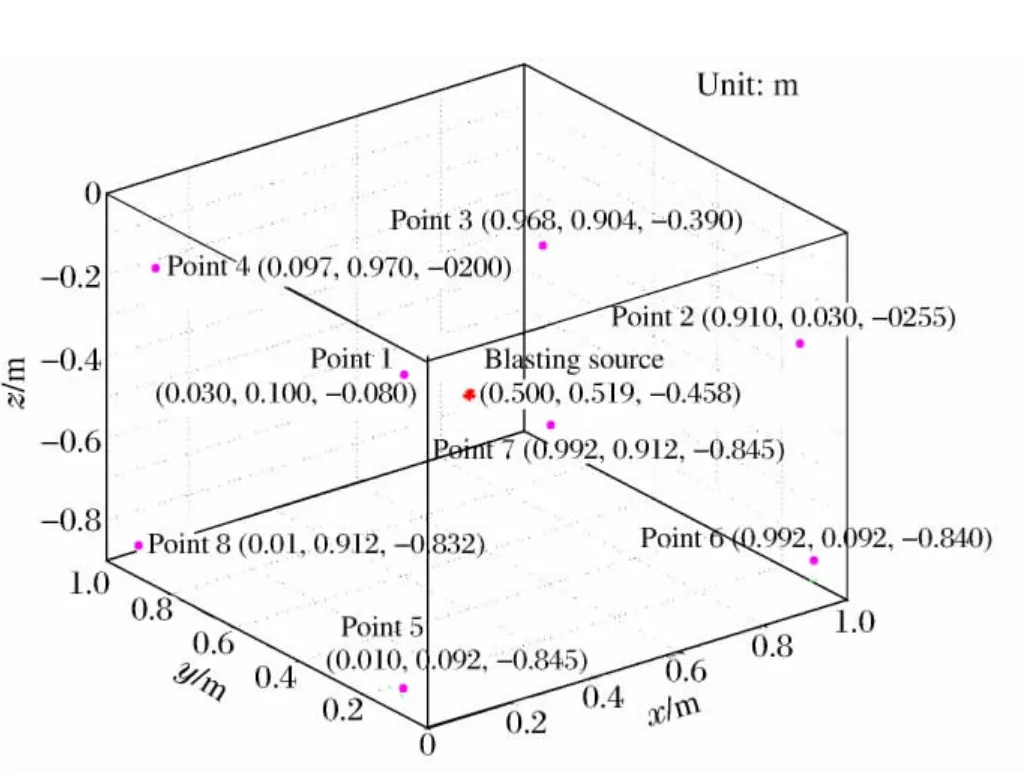
圖3 測點布置及爆源定位計算結果三維圖Fig.3 Agraphical model for observation point layout and computed blasting source position

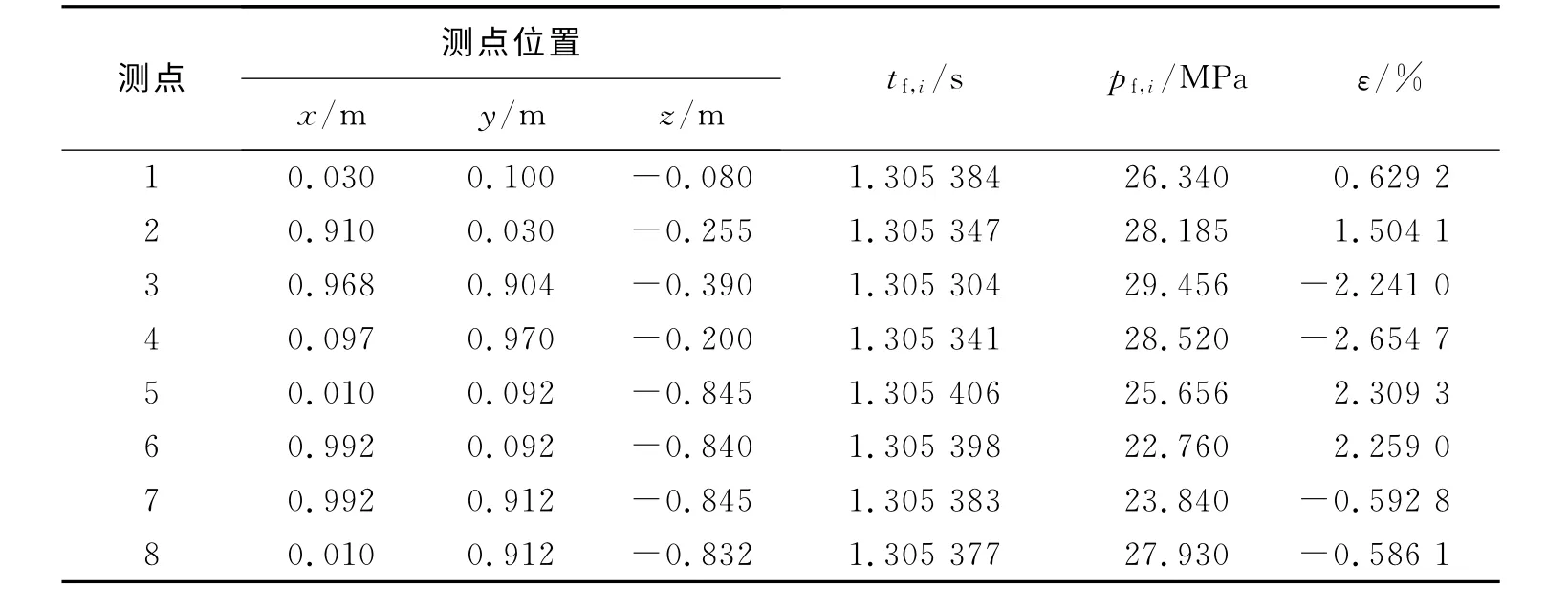
表1 測點布置及測量結果原始數據表Table 1Initial data of observation point layout and measured results

3 計算誤差分析

爆源定位計算中，不計人工計量誤差，誤差影響因素主要有測點數據的準確性、測點布設的紊亂度、水中沖擊波傳播速度和壓力峰值的計算誤差、測點數量。

3.1 測點數據的準確性

一般而言，傳感器測量結果的準確性對計算結果應該有較大的影響。將前述實例中的實測數據對測點進行排序，結果如表2所示。由表2可以看出，根據水中沖擊波傳播規律，3種排序方式的結果應該是一致的，但實際測量結果并不一致，說明壓力傳感器測得的數據不理想，實際計算中可以根據情況找出測量結果明顯有問題的測點進行剔除，但有時卻難以判斷。

表2 根據不同的排序方式對測點排序表Table 2Sequence of observation point by different methods

為了進一步分析個別測點數據的準確性對計算誤差的影響程度，人為修改測點2的壓力峰值pm，2為測量值pf，2的3倍時，計算結果仍未改變；將測點2與測點3的時間差Δtm，2人為修改為測量值Δtf，2的0.6倍逐漸增加到8倍時，計算爆源至各測點距離誤差絕對值的平均值εd的變化曲線如圖4所示。從圖中可以看出，當測量值達到真值的2倍以上時，計算誤差才開始有明顯的變化。

從上述分析可以看出，個別測點即使有較大的誤差，對本方法的計算結果仍不會產生較大的影響。

3.2 測點布設的紊亂度

測點布設的紊亂度從兩個方面來考慮：爆源與各測點之間的連線所形成方位角的離散程度；爆源與各測點之間距離的離散程度。測點布設的紊亂度可用這些距離的標準差來衡量。從定位計算方法分析，測點布設的紊亂度越大，計算誤差越小。如圖5所示，當方位角離散程度較小時，即爆源在傳感器布置范圍之外，且爆源與傳感器之間的距離大于傳感器布置范圍本身的尺寸，而不是傳感器布置在爆源四周，在爆源與各測點之間的連線所形成方位角不變的情況下，圖6給出了系列驗證性實驗中爆源與各測點之間距離的標準差σD對計算誤差εd的影響。

不難看出，爆源與各測點之間距離的標準差越大，測點布設的紊亂度就越大，計算誤差就越小。

3.3 水中沖擊波傳播速度及壓力峰值的計算誤差

實際計算中，本文中提到的水中沖擊波傳播速度及壓力峰值計算模型中各參數都是通過大量實驗擬合而成的，與實際工程之間具有很高的吻合度，因此計算結果也具有很高的精度，在測點布設紊亂度較大、測量結果正常時，定位計算誤差約0.5%。

為分析模型參數誤差對定位計算的影響，更改了上述2個模型的結果，結果表明，當模型計算結果誤差在±5%時，定位計算誤差改變不明顯。可能是在該定位計算過程中1.2.3節所述的是將合計均方根最小值對應的節點處即為本輪計算確定的爆源位置，而不對此最小值規定為某一值，使得在計算過程中誤差互相抵消，這正是本方法計算精度高的原因。

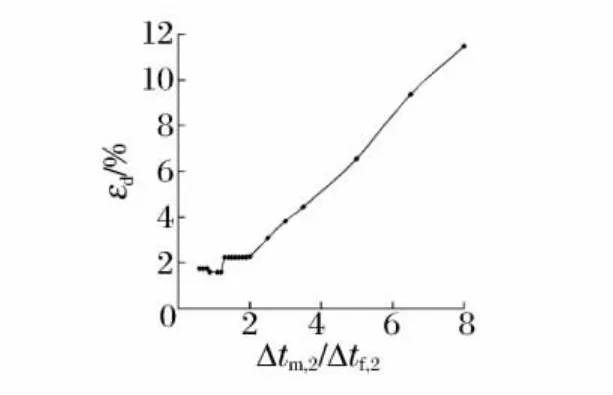
圖4 測點2與3的時間差變化量對定位計算誤差的影響曲線圖Fig.4Influnce of time difference between observation points 2and 3on error

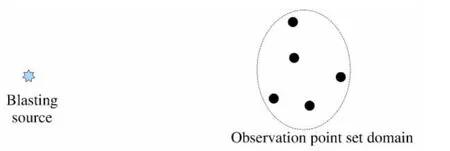
圖5 小方位角離散度布置示意圖Fig.5Influnce of small－azimuth dispersion on error

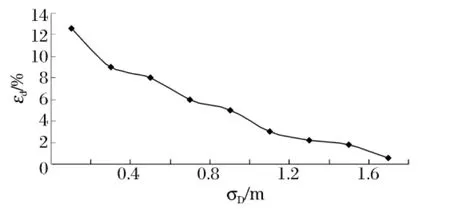
圖6 爆源與各測點之間距離的標準差對定位計算誤差的影響Fig.6Influnces of distance standard dievation between blasting source and observation points on error

3.4 測點的數量

本方法要求測點數量至少4個才能有解，通過對實驗數據進行計算分析，在測量數據比較正常的情況下，得出測點數量對計算誤差εd的影響如圖7所示。從圖中可以看出，有效測點數量對計算精度并無明顯的影響。多次計算表明，測點數達到8個即可達到很高的計算精度。

4 結 論

通過現場實踐和分析說明，采用最小誤差逼近法對水下爆源定位計算是可靠的，在有效數據不小于4個的情況下，完全可以滿足現場測量的要求；該方法在個別測量數據準確性較差的情況下，仍能得出較好的計算結果，使得該方法具有較強的可行性；在測點布設時應盡量加大布置的紊亂度，通過對觀測數據進行分析，盡量剔除無效的傳感器觀測數據，以提高計算精度。

［1］ 李兵，王巍，房毅.GPS RTK 技術在艦船抗沖擊試驗中的應用［J］.海洋測繪，2009，29（2）：53－55.Li Bing，Wang Wei，Fang Yi.Application of GPS RTK to ship shock trial［J］.Hydrographic Surveying and Charting，2009，29（2）：53－55.

［2］ 劉基余，李征航，王躍虎.全球定位系統原理及其應用［M］.北京：測繪出版社，1993：20－28.

［3］ 余小龍，胡學奎.GPS RTK 技術的優缺點及發展前景［J］.測繪通報，2007（10）：39－42.Yu Xiao－long，Hu Xue－kui.GPS RTK technique：Merits，demerits and perspective［J］.Bulletin of Surveying and Mapping，2007（10）：39－42.

［4］ Mizugaki K，Fujiwara R，Nakagawa T，et al.Accurcte wireless location／commution system with 22－cm error using UWB－IR［C］∥Symposium on Radio and Wireless，2007IEEE.Long Beach，2007：455－458.

［5］ Kang D，Namgoong Y，Yang S，et al.A simple asynchronous UWB position location algorithm based on single round－trip，transmission［C］∥8th International Conference Advanced Communication Technology，ICACT 2006－Proceedings.Korea：Phoenix Park，2006：1458－1461.

［6］ 李兵，朱興邦，侯寶娥.基于沖擊波測量的水下爆源定位方法研究［J］.測繪科學，2009，34增刊：26－28.Li Bing，Zhu Xing－bang，Hou Bao－e.Positioning method of underwater explosion source based on shock wave measuring［J］.Science of Surveying and Mapping，2009，34suppl：26－28.

［7］ 張振華，朱錫，白雪飛.水下爆炸沖擊波的數值模擬研究［J］.爆炸與沖擊，2004，24（2）：182－188.Zhang Zhen－hua，Zhu Xi，Bai Xue－fei.The study on numerical simulation of underwater blast wave［J］.Explosion and Shock Waves，2004，24（2）：182－188.