基于有效獨立的改進傳感器優(yōu)化布置方法研究

劉 偉，高維成，李 惠，孫 毅

(1.哈爾濱工業(yè)大學(xué) 航天科學(xué)與力學(xué)系，哈爾濱 150001;2.哈爾濱工業(yè)大學(xué) 土木工程學(xué)院，哈爾濱 150090)

結(jié)構(gòu)健康監(jiān)測系統(tǒng)主要是通過布置在結(jié)構(gòu)上的傳感器采集數(shù)據(jù)并進行結(jié)構(gòu)模態(tài)參數(shù)識別、有限元模型修正、損傷識別和結(jié)構(gòu)健康狀況評估。隨著結(jié)構(gòu)健康監(jiān)測技術(shù)的發(fā)展，傳感器在結(jié)構(gòu)中的優(yōu)化布置問題［1-7］日趨突出，即如何用有限數(shù)量的傳感器從被噪聲污染的信號中采集到最充分和最有價值的振動信息。大型復(fù)雜結(jié)構(gòu)自由度數(shù)多、動力特性復(fù)雜、準確測量振動信息較難，必須采用適當(dāng)?shù)膬?yōu)化方法來確定最優(yōu)傳感器布置位置，以至于測試的響應(yīng)信息更完備、識別的模態(tài)參數(shù)更準確、構(gòu)建的健康監(jiān)測系統(tǒng)更高效。

目前文獻中出現(xiàn)的傳感器優(yōu)化布置方法種類繁多，很難將其毫無遺漏的歸納分類。劉福強等［1］對作動器/傳感器優(yōu)化布置的研究進展進行了較好的歸納總結(jié)，闡述了作動器/傳感器的優(yōu)化布置準則和常用的優(yōu)化計算方法;Staszewski［2］從組合優(yōu)化、神經(jīng)網(wǎng)絡(luò)和信息理論三個角度綜述了傳感器優(yōu)化布置方法在復(fù)合材料損傷監(jiān)測方面的研究進展，并通過一個簡單案例驗證了方法的有效性;李東升等［3］比較了較常用的傳感器布置方法，揭示了各種方法間的內(nèi)在聯(lián)系，利用一梯形結(jié)構(gòu)考察了不同傳感器布置方法結(jié)果的異同。有效獨立法(Effective Independence-EI)［8-9］是目前應(yīng)用最為廣泛的一種傳感器布置方法，它以每個傳感器測點對模態(tài)向量線性獨立的貢獻最大為目標，逐步刪除有效獨立向量具有最小值的自由度，由此來優(yōu)化Fisher信息矩陣，使感興趣的模態(tài)向量在最少測點的情況下，盡可能保持線性獨立，從而在測試中用有限的傳感器可以獲取到最大的模態(tài)信息。模態(tài)動能法(Modal Kinetic Energy-MKE)［10］則發(fā)展了傳統(tǒng)的以結(jié)構(gòu)振幅較大位置布置傳感器的經(jīng)驗法，以測得的模態(tài)動能最大為目標來選擇傳感器的位置，可提高結(jié)構(gòu)動態(tài)響應(yīng)測量時的信噪比。

有效獨立法和模態(tài)動能法均屬于傳統(tǒng)傳感器優(yōu)化布置算法，在實際測試中應(yīng)用較多，但二者又都有各自的局限性。有效獨立法不依賴于優(yōu)化搜索技術(shù)，從有限元模態(tài)矩陣出發(fā)選擇用于識別目標模態(tài)的最佳測點組合。但是傳感器不一定分布在模態(tài)動能較大的位置，從而可能會丟失反映結(jié)構(gòu)真實狀態(tài)的重要參數(shù)信息。而模態(tài)動能法則嚴重依賴于有限元網(wǎng)格劃分，如果劃分較粗，傳感器將分布較遠，如果劃分較細，傳感器將分布過近。目前很多學(xué)者對上述算法均提出了改進:Li等［11］提出一個通過正交三角分解快速計算有效獨立法系數(shù)的方法，避免了傳統(tǒng)的有效獨立法計算中所需要的對信息陣進行特征值分解或者計算矩陣逆，克服了其計算量大的缺點;Imamovic［12］為克服EI法不足，即布置結(jié)果中可能包含一些振動能量很低的測點，在EI法中計算有效獨立分布向量的分量上乘以一個加權(quán)系數(shù)，即驅(qū)動點留數(shù)DPR(Driving Point Residue)，并稱其為有效獨立-驅(qū)動點留數(shù)法(EFI-DPR);吳子燕等［13］提出了以單位剛度的模態(tài)應(yīng)變能作為驅(qū)動點殘差系數(shù)來修正有效獨立法(EI)的傳感器布置方案，稱之為有效獨立-驅(qū)動點殘差法(EFI-DPR)。

綜合考慮有效獨立法和模態(tài)動能法的優(yōu)缺點，本文從多自由度系統(tǒng)頻響函數(shù)矩陣的模態(tài)展開式出發(fā)，推導(dǎo)了平均位移幅值、平均速度幅值和平均加速度幅值公式［14］，提出兩種基于有效獨立的改進傳感器優(yōu)化布置方法:有效獨立-平均加速度幅值法(Effective Independence-Average Acceleration Amplitude，EI-AAA)和有效獨立-模態(tài)動能法(Effective Independence-Modal Kinetic Energy，EI-MKE)，并與有效獨立法［8-9］、模態(tài)動能法［10］、有效獨立驅(qū)動點留數(shù)法［12］、有效獨立驅(qū)動點殘差法［13］等方法進行了比較研究。文中以實際鋼井字梁采光頂結(jié)構(gòu)為算例，運用模態(tài)動能和平均加速度幅值準則、Fisher信息矩陣行列式最大準則、截斷模態(tài)矩陣條件數(shù)準則、MAC矩陣非對角線元素平均值和最大值準則評價各種優(yōu)化布置方法的優(yōu)劣。

1 傳統(tǒng)傳感器優(yōu)化布置方法

1.1 有效獨立法(EI)

有效獨立法［8-9］(EI)首先根據(jù)模態(tài)動能法(MKE)初選傳感器布置的候選集合，然后從模態(tài)坐標估計誤差協(xié)方差最小準則出發(fā)，依次去除對模態(tài)線性獨立貢獻最小的自由度，最終獲得使模態(tài)空間估計最佳的傳感器較優(yōu)布置方案。

有效獨立法通過求解矩陣ΦTΦ(Fisher信息矩陣Q的等價矩陣)的特征方程，構(gòu)造了有效獨立矩陣EI，如下:

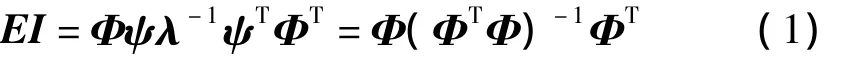
其中，λ是矩陣ΦTΦ的特征值矩陣，ψ是矩陣ΦTΦ的特征向量矩陣。

顯然，EI是冪等矩陣，它的跡等于秩，其對角線上第i個元素表示第i個自由度對矩陣EI秩的貢獻。因此，定義矩陣EI的對角線元素組成的列向量為有效獨立向量EIV(Effective Independence Vector)，元素值滿足0≤EIii≤1。如果EIii接近于0，則該自由度對目標模態(tài)的線性獨立性貢獻較小，應(yīng)該去除;如果EIii接近于1，則該自由度對目標模態(tài)的線性獨立性貢獻較大，應(yīng)該保留。有效獨立法就是這樣從全部自由度中逐步迭代刪除對有效獨立向量貢獻最小的自由度，保留對有效獨立向量貢獻較大的自由度，直到得到傳感器的較優(yōu)布置方案。

1.2 模態(tài)動能法(MKE)

模態(tài)動能法的基本思想是模態(tài)動能較大位置其動態(tài)響應(yīng)也較大，將傳感器布置在該自由度上有利于信號采集和模態(tài)參數(shù)識別。因此，其布置傳感器目標準則就是尋求縮減的傳感器測點集合從而使結(jié)構(gòu)在這些測點處的模態(tài)動能最大。

模態(tài)動能的表達式如下:

式中，Φ∈Rn×p是模態(tài)矩陣，p是目標模態(tài)數(shù)。因此，對所有目標模態(tài)的模態(tài)動能貢獻度較大的自由度位置集合可以選作傳感器的候選集合。

對質(zhì)量矩陣M進行正交Cholesky分解(M=LTL)，并令=LΦ，則模態(tài)動能的表達式可以寫為:

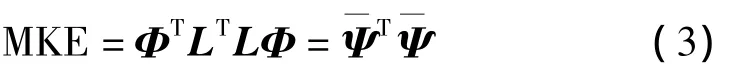
可見，模態(tài)動能表達式(3)與Fisher信息矩陣表達式(1)相似，區(qū)別僅在于對信息矩陣的加權(quán)矩陣不同，對于模態(tài)動能法，加權(quán)矩陣是有限元質(zhì)量矩陣M;對于有效獨立法，加權(quán)矩陣是傳感器測試噪聲協(xié)方差的逆矩陣。

2 驅(qū)動點頻響函數(shù)的近似表達式

多輸入多輸出位移頻響函數(shù)矩陣的模態(tài)展開式可寫成如下形式:

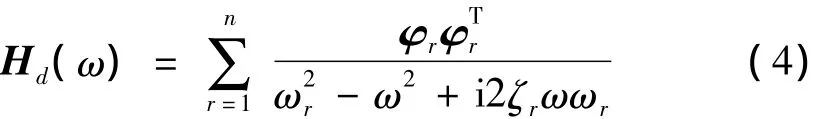
其中，Hd(ω)∈Cn×n是位移頻響函數(shù)矩陣，Φ∈Rn×n是質(zhì)量歸一化實模態(tài)矩陣，φr∈Rn×1是第r階質(zhì)量歸一化實模態(tài)，ζr∈Rn×1是第r階模態(tài)阻尼比。上述頻響函數(shù)表達式是全部模態(tài)的疊加，計算時采用完整模態(tài)集合。但對于實際結(jié)構(gòu)，計算或識別出所有模態(tài)是不現(xiàn)實的。而且，并非所有模態(tài)對響應(yīng)的貢獻都相同，高階模態(tài)對低頻響應(yīng)影響就很小。因此，通常采用模態(tài)截斷法即采用非完整模態(tài)集合計算式(4)，如下:

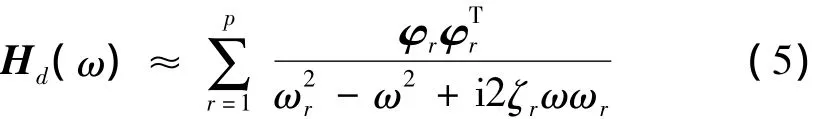
其中，p為考慮的模態(tài)數(shù)目。

假定環(huán)境激勵輸入是穩(wěn)態(tài)白噪聲，則其頻譜為常數(shù)。因此，對于線性系統(tǒng)，位移響應(yīng)幅值與頻率函數(shù)幅值成正比。若進一步假設(shè)各階模態(tài)阻尼近似相等，則結(jié)構(gòu)在環(huán)境激勵下的位移響應(yīng)與下式成正比:

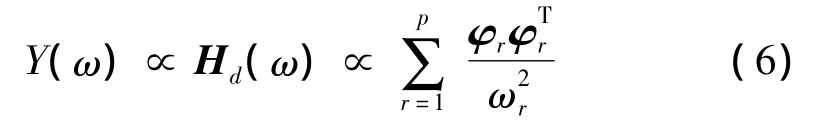
其中，Y(ω)為輸出位移響應(yīng)頻譜。由于位移、速度及加速度頻響函數(shù)之間存在如下關(guān)系:

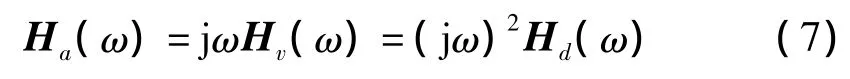
因此，結(jié)構(gòu)在環(huán)境激勵下的速度響應(yīng)與下式成正比:

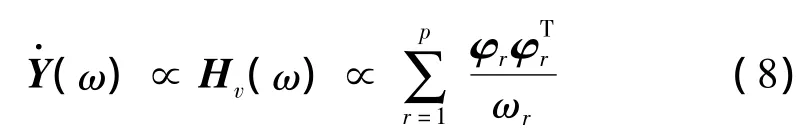
結(jié)構(gòu)在環(huán)境激勵下的加速度響應(yīng)與下式成正比:

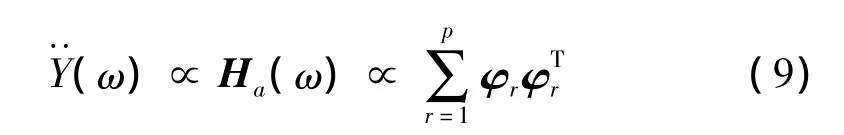
本文分別定義式(6)、式(8)和式(9)為平均位移幅值(Average Displacement Amplitude-ADA)矩陣、平均速度幅值(Average Velocity Amplitude-AVA)矩陣和平均加速度幅值(Average Acceleration Amplitude-AAA)矩陣。因此，結(jié)構(gòu)第i自由度的位移、速度和加速度響應(yīng)相對大小可分別用上述三式的對角線元素來表示，具體如下:

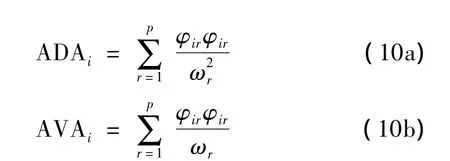
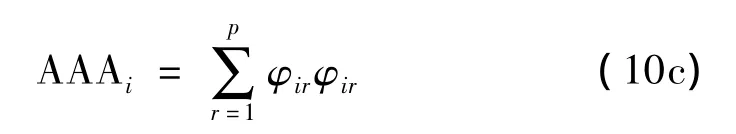
實際上，式(10)就是第i點激勵第i點響應(yīng)的驅(qū)動點頻響函數(shù)的近似表達。

3 改進傳感器優(yōu)化布置方法

3.1 有效獨立-平均加速度幅值法(EI-AAA)

結(jié)構(gòu)模態(tài)測試時一般都采用加速度傳感器，而加速度信號可以很方便轉(zhuǎn)化為速度和位移信號。因此，在布置最佳測試點位置時，應(yīng)該使布置測點具有較大的平均加速度幅值(AAAi值)。如果僅保證布置測點的平均加速度幅值最大，則可能會使測試模態(tài)之間的線性獨立性變差。有效獨立法目的是使測試模態(tài)盡可能線性獨立，在具體實施中，僅考慮測試自由度對截斷模態(tài)秩的貢獻而不考慮其他任何需求，因此EI法選擇的測試自由度往往比平均加速度幅值小。為克服EI法布置結(jié)果中可能包含具有較低響應(yīng)測點的不足，本文提出有效獨立-平均加速度幅值法(Effective Independence-Average Acceleration Amplitude，EI-AAA)，如(11)式所示，它綜合二者優(yōu)點，使優(yōu)化測點集合具有盡可能高的平均加速度幅值，即測試響應(yīng)較大，同時盡可能保證測試模態(tài)線性獨立。

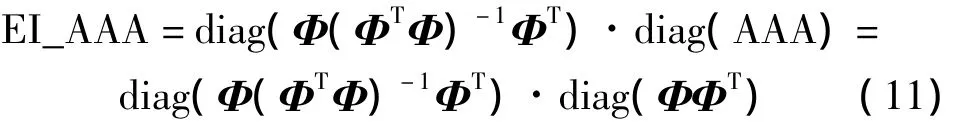
有效獨立-平均加速度幅值法在具體操作時與有效獨立法一樣，都需要通過循環(huán)使截斷模態(tài)矩陣保持滿秩。主要不同就是在選擇對截斷模態(tài)矩陣秩貢獻最小自由度時用每個自由度的平均加速度幅值進行加權(quán)修正，目的是率先去除具有最低加速度響應(yīng)的自由度。但需要說明的是:結(jié)構(gòu)每個自由度的平均加速度幅值不會因為循環(huán)操作而發(fā)生改變。

3.2 有效獨立-模態(tài)動能法(EI-MKE)

如前所述，平均加速度幅值具有能量的概念，若假設(shè)結(jié)構(gòu)具有單位一致質(zhì)量矩陣(M=I)，則其與模態(tài)動能表達式相同。因此，平均加速度幅值表達的模態(tài)動能沒有考慮結(jié)構(gòu)具體質(zhì)量分布情況對模態(tài)動能大小的影響。因此，本文又提出有效獨立-模態(tài)動能法(Effective Independence-Modal Kinetic Energy，EI-MKE)，直接用模態(tài)動能向量與有效獨立向量相乘對其進行修正，考慮質(zhì)量分布的影響。操作過程與有效獨立-平均加速度幅值法相同，表達式如下:

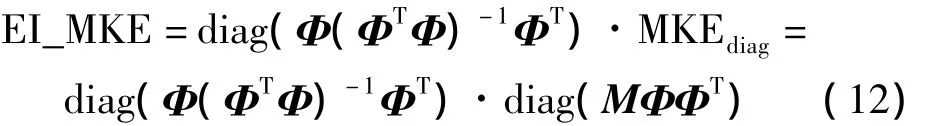
3.3 有效獨立-驅(qū)動點留數(shù)法［12］(EFI-DPR)

Imamovic［12］為克服EI法其測點位置能量過低導(dǎo)致信息丟失的缺點，在EI法中計算有效獨立向量的分量上乘以一個加權(quán)系數(shù)，其定義為平均驅(qū)動自由度速度(Average Driving DOF Velocity-ADDOFV)，表達式如下:

式(13)也稱驅(qū)動點留數(shù)DPR(Driving Point Residue)，該方法被稱為有效獨立-驅(qū)動點留數(shù)法(EFI-DPR)，總體表達式如(14)式所示，操作過程與有效獨立法相同。

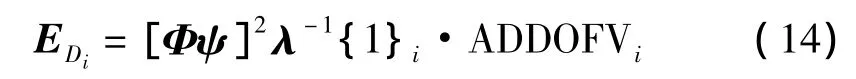
可以看出，文獻［12］所采用的驅(qū)動點留數(shù)DPR表達式式(13)與本文定義的平均速度幅值(Average Velocity Amplitude-AVA)的表達式式(10b)相同。

3.4 有效獨立-驅(qū)動點殘差法［13］(EFI-DPR)

吳子燕等［13］為克服有效獨立法測得的模態(tài)動能不高而可能造成信息丟失的缺點，提出了有效獨立-驅(qū)動點殘差(Drive Point Residue)法。它是以單位剛度的模態(tài)動能作為驅(qū)動點殘差系數(shù)(CDPRi)來加權(quán)修正有效獨立法(EFI)的傳感器布置方案。

其定義有效獨立驅(qū)動點殘差系數(shù)CDPRi為單元剛度的模態(tài)動能，即

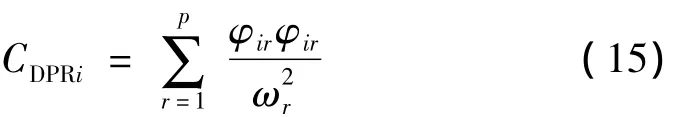
得到有效獨立-驅(qū)動點殘差(EFI-DPR)法的有效獨立分配向量為:

該方法操作過程也與有效獨立法相同，即進行迭代求解。可以看出，文獻［13］所采用的驅(qū)動點殘差系數(shù)DPR表達式(15)式與本文定義的平均位移幅值(Average Displacement Amplitude-ADA)的表達式(10a)式相同。

3.5 四種方法的對比分析

觀察式(10)可以看出，式(10c)所示的平均加速度幅值表達式具有振型能量的含義，其相當(dāng)于結(jié)構(gòu)具有單位一致質(zhì)量矩陣(M=I)的第i個自由度的模態(tài)動能;而式(10b)所示的平均速度幅值表達式則相當(dāng)于以每階固有頻率平方根對每階模態(tài)進行除權(quán)，然后再計算振型能量;同樣，式(10a)所示的平均位移幅值表達式則相當(dāng)于用每階固有頻率對每階模態(tài)進行除權(quán)，然后再計算振型能量。顯然，模態(tài)動能較大的位置其動態(tài)響應(yīng)也大，傳感器測點應(yīng)該布置于這些自由度上。而式(10c)平均加速度幅值表示的結(jié)構(gòu)第i個自由度模態(tài)動能大小與每階模態(tài)第i個元素φir的大小密切相關(guān)，φir越大，則第i自由度平均加速度幅值越大，也即具有單位一致質(zhì)量矩陣的結(jié)構(gòu)第i自由度模態(tài)動能越大。

一般情況下，結(jié)構(gòu)每階振型幅值都處于同一數(shù)量級，每階模態(tài)向量的元素值相差不大。因此，每階模態(tài)對式(10c)數(shù)值大小的貢獻基本相當(dāng)，即式(10c)的第i自由度平均加速度幅值能夠考慮所有可測模態(tài)的貢獻。

式(10b)平均速度幅值表達的結(jié)構(gòu)第i個自由度模態(tài)動能大小與每階模態(tài)以每階固有頻率平方根除權(quán)后的第i個元素φir/大小相關(guān)，顯然，除權(quán)后結(jié)構(gòu)高階模態(tài)對結(jié)構(gòu)第i個自由度模態(tài)動能大小貢獻較小，模態(tài)動能主要集中于結(jié)構(gòu)低階模態(tài)。文獻［12］的研究結(jié)果也驗證了這一點，它們的優(yōu)化布置測點主要集中于結(jié)構(gòu)的低階模態(tài)。

同樣，式(10a)的平均位移幅值表達與每階模態(tài)以每階固有頻率除權(quán)后的第i個元素φir/ωr大小相關(guān)，高低階模態(tài)除權(quán)后對結(jié)構(gòu)第i個自由度模態(tài)動能大小貢獻將更加分化，模態(tài)動能集中于低階模態(tài)，甚至可能僅第一階模態(tài)對模態(tài)動能貢獻較大，其余階模態(tài)貢獻極小甚至可以忽略。文獻［13］的優(yōu)化布置測點已經(jīng)集中于第一階振型的模態(tài)動能最大位置，測點過于集中，不利于其他階振型的識別。

綜上，本文提出的選擇平均加速度幅值對有效獨立法進行加權(quán)處理是合理的，即考慮測試模態(tài)線性獨立，又盡可能考慮所有模態(tài)對模態(tài)動能的貢獻，滿足較優(yōu)布置測點具有較大能量的要求。此外，本文提出的模態(tài)動能對有效獨立法進行加權(quán)處理更是合理的，它還考慮了結(jié)構(gòu)具體質(zhì)量分布情況的影響，更具有實際意義。

4 傳感器優(yōu)化布置方法評價準則

對傳感器優(yōu)化布置算法和傳感器布置方案的優(yōu)劣進行評價，需要建立相應(yīng)的評價準則，下面闡述一下本文中采用的傳感器優(yōu)化布置評價準則。

4.1 模態(tài)動能

結(jié)構(gòu)的模態(tài)動能并不是平均分配到結(jié)構(gòu)的各個模態(tài)中，在結(jié)構(gòu)的各個待選自由度上的分配也不均勻。模態(tài)動能準則希望結(jié)構(gòu)較優(yōu)測點所包含的結(jié)構(gòu)模態(tài)動能較大，這樣才能保證測試信號的信噪比較高，抗噪聲干擾的能力較強，也才能保證模態(tài)識別結(jié)果精度較高，計算公式如式(2)所示。

4.2 平均加速度幅值

平均加速度幅值準則能保證傳感器布設(shè)在結(jié)構(gòu)響應(yīng)的幅值點，有利于數(shù)據(jù)的采集和提高測量的抗噪能力。在布置最佳測試點位置時，應(yīng)該使布置測點具有較大的平均加速度幅值(AAAi值)，這是本文提出的一種傳感器評價準則，計算公式如式(10c)所示。

4.3 Fisher信息矩陣行列式

Fisher信息矩陣Q最大等價于模態(tài)坐標估計誤差的協(xié)方差J最小，而Fisher信息矩陣Q跡或行列式值最大時的估計是模態(tài)坐標的無偏估計。同時，F(xiàn)isher信息矩陣Q也度量了測試響應(yīng)中所包含信息的多少，其行列式值越大，其所包含的模態(tài)信息越多。因此，可以采用Fisher信息矩陣Q的行列式值的大小來評價傳感器布置方案的好壞。

4.4 截斷模態(tài)矩陣條件數(shù)

矩陣條件數(shù)是判斷矩陣病態(tài)與否的一種度量，條件數(shù)越大矩陣越病態(tài)。因此，可以采用截斷模態(tài)矩陣條件數(shù)來判斷截斷模態(tài)矩陣的好壞程度，即截斷測試模態(tài)集的線性獨立性程度，因此它也是從模態(tài)向量線性獨立性的角度考查所選測點優(yōu)劣的指標。從線性代數(shù)的分析可知，矩陣的條件數(shù)總是大于1。正交矩陣的條件數(shù)等于1，奇異矩陣的條件數(shù)為無窮大，而病態(tài)矩陣的條件數(shù)則為比較大的數(shù)據(jù)。因此，截斷模態(tài)矩陣條件數(shù)越接近于1越好。

4.5 模態(tài)置信準則

模態(tài)置信準則是評價模態(tài)向量交角的一種數(shù)學(xué)工具，可用來判別結(jié)構(gòu)實測模態(tài)向量相互線性獨立的評價指標，其數(shù)學(xué)公式如下:

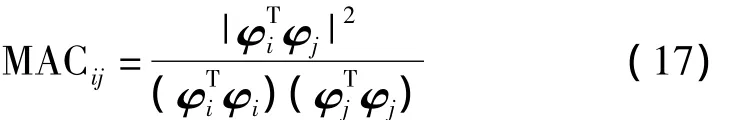
式中，φi和φj分別是第i階和第j階模態(tài)向量。檢查模態(tài)置信準則MAC矩陣的非對角線元素，就可以知道截斷實測模態(tài)的線性獨立程度。本文分別采用MAC矩陣非對角線元素平均值和最大值作為評價指標，二者數(shù)值越小越好。

5 仿真算例

5.1 鋼井字梁采光頂結(jié)構(gòu)實例

圖1所示為一實際鋼井字梁采光頂結(jié)構(gòu)，結(jié)構(gòu)尺寸9 m×9 m，網(wǎng)格數(shù)9×9，H型鋼截面尺寸H300×250×6×8，鋼材型號Q235B，彈性模量206 GPa，密度7 850 kg/m3，計算時將荷載簡化成集中質(zhì)量作用于結(jié)構(gòu)節(jié)點上。結(jié)構(gòu)約束形式為四邊簡支，井字梁節(jié)點按剛接處理。計算模型具有100個節(jié)點，180個單元，544個自由度。采用子空間迭代法對井字梁采光頂結(jié)構(gòu)進行模態(tài)分析，提取感興趣的前五階振型和固有頻率，如圖2所示。可以看出，該結(jié)構(gòu)振型為標準的四邊簡支板結(jié)構(gòu)振型:第一階是板的一階彎曲模態(tài)、第二階為板對角線方向的二階彎曲模態(tài)、第三階是另一個對角線方向的二階彎曲模態(tài)(第二階的重頻模態(tài))、第四階是x方向和y方向各二階彎曲模態(tài)的組合模態(tài)、第五階是對角線方向各三階彎曲模態(tài)的組合模態(tài)。

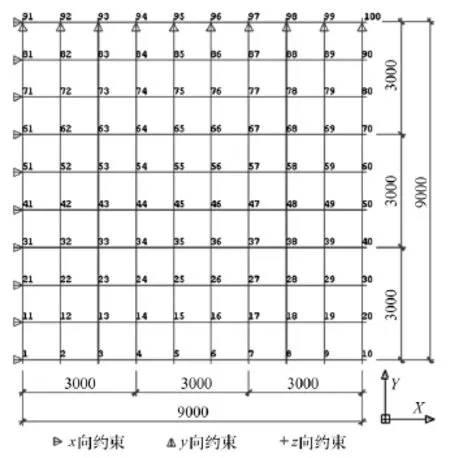
圖1 鋼井字梁采光頂結(jié)構(gòu)Fig.1 Cross beam sunroof structure

5.2 傳感器優(yōu)化布置方案

井字梁采光頂結(jié)構(gòu)的有限元建模采用梁單元，每個節(jié)點有6個自由度。觀察圖2可知，結(jié)構(gòu)所有振型都是豎向的，即z向為該結(jié)構(gòu)振動的主自由度方向。為此，提取該結(jié)構(gòu)中間所有節(jié)點z向自由度為候選測試自由度集合，將其重新編號如圖3所示，可測自由度為64個。

圖2 鋼井字梁采光頂結(jié)構(gòu)有限元計算振型Fig.2 Mode shapes of cross beam sunroof structure by FEM

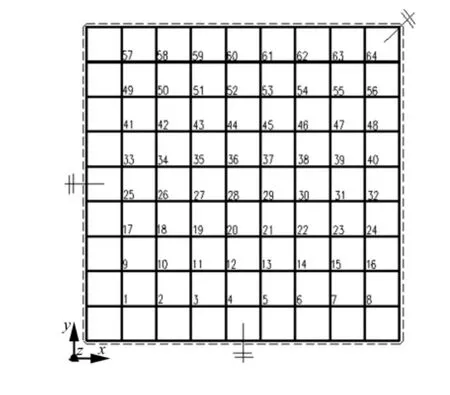
圖3 可測自由度重新編號Fig.3 New numbers of the measurable DOF

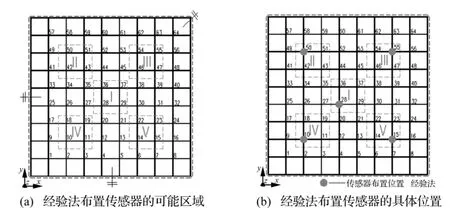
圖4 經(jīng)驗法布置傳感器Fig.4 Optimal sensor placement by personal experience

由系統(tǒng)可觀性原則可知，測試結(jié)構(gòu)的前五階模態(tài)最少需要5個傳感器。為此，本文給定傳感器個數(shù)為5個，并在輸入數(shù)據(jù)中考慮5%的隨機噪聲影響。實際上，本文所研究的結(jié)構(gòu)形式比較簡單，根據(jù)前五階模態(tài)的振動形態(tài)完全可以根據(jù)個人經(jīng)驗對其進行初步布置。選此結(jié)構(gòu)作為仿真算例主要是為了便于比較分析本文方法的優(yōu)越性。依據(jù)筆者經(jīng)驗，不采用任何優(yōu)化算法，初步確定5個傳感器的布置區(qū)域如圖4(a)中5個虛線方框所示。若要具體確定，筆者會主觀選擇10、15、50、55和Ⅰ號區(qū)域中任意一個(結(jié)構(gòu)完全對稱導(dǎo)致Ⅰ號區(qū)域四個節(jié)點地位完全相同)共5個作為傳感器的布置位置，見圖4(b)。顯然，Ⅱ、Ⅲ、Ⅳ、Ⅴ號區(qū)域中的四個節(jié)點的地位是不同的，選擇哪些節(jié)點組合會使測試模態(tài)的線性獨立性最大、選擇哪些節(jié)點組合會使測試模態(tài)的模態(tài)動能最大、選擇哪些節(jié)點組合會使測試模態(tài)的平均加速度幅值最大，這些信息根據(jù)經(jīng)驗是不能獲取的，必須采用優(yōu)化方法進行選擇。

基于此，本文采用前文所述的有效獨立法、模態(tài)動能法、有效獨立-平均加速度幅值法、有效獨立-模態(tài)動能法、有效獨立驅(qū)動點留數(shù)法［12］、有效獨立驅(qū)動點殘差法［13］對該井字梁采光頂結(jié)構(gòu)進行傳感器優(yōu)化布置，得到各方法的傳感器優(yōu)化布置方案如圖5所示。

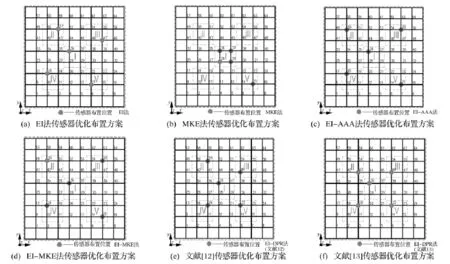
圖5 各種方法的傳感器優(yōu)化布置方案Fig.5 Optimal sensor placement scheme of all methods

5.3 對比分析與討論

為方便對比分析，繪制結(jié)構(gòu)前五階模態(tài)的模態(tài)動能分布圖和平均加速度幅值分布圖，見圖6。該結(jié)構(gòu)前五階模態(tài)的模態(tài)動能分布和平均加速度幅值分布基本一致，這是由于結(jié)構(gòu)對稱和梁截面尺寸相同導(dǎo)致的結(jié)構(gòu)質(zhì)量矩陣對角線元素都相同所引起的。如圖6所示，結(jié)構(gòu)動能和平均加速度幅值最大的節(jié)點為Ⅰ號區(qū)域內(nèi)的四個節(jié)點(28、29、36、37)，接著是Ⅱ、Ⅲ、Ⅳ、Ⅴ號區(qū)域內(nèi)結(jié)構(gòu)對角線上靠近四角點的四個節(jié)點(15、50、55、10)，然后是Ⅱ、Ⅲ、Ⅳ、Ⅴ號區(qū)域內(nèi)垂直于結(jié)構(gòu)對角線的八個節(jié)點(14、18、47、51、11、23、42、54)，再次是Ⅱ、Ⅲ、Ⅳ、Ⅴ號區(qū)域內(nèi)結(jié)構(gòu)對角線上靠近中央的四個節(jié)點(20、43、46、19)，最后依次是圖中等高線分布的其余節(jié)點。

圖6 結(jié)構(gòu)前五階模態(tài)的模態(tài)動能和平均加速度幅值分布圖Fig.6 MKE and AAA distribution of the first five mode shapes in the structure

觀察圖5可以看出，所有方法得到的傳感器布置位置都在上述經(jīng)驗法確定的傳感器可能布置區(qū)域之中。有效獨立法確定的傳感器位置在井字梁結(jié)構(gòu)上旋轉(zhuǎn)對稱等間距分布，但Ⅱ、Ⅲ、Ⅳ、Ⅴ號區(qū)域內(nèi)四個測點卻處于模態(tài)動能(平均加速度幅值)第三大的節(jié)點群;模態(tài)動能法確定的傳感器位置主要集中Ⅰ號區(qū)域內(nèi)的四個節(jié)點，模態(tài)動能最大;有效獨立-平均加速度幅值法和有效獨立-模態(tài)動能法的傳感器布置結(jié)果相同，與有效獨立法結(jié)果比較，其中三個傳感器的位置發(fā)生改變，從模態(tài)動能(平均加速度幅值)第三大節(jié)點群轉(zhuǎn)移到了模態(tài)動能(平均加速度幅值)第二大節(jié)點群。總體模態(tài)動能(平均加速度幅值)有所提高，介于有效獨立法和模態(tài)動能法之間。即保證了所測模態(tài)向量的最大線性獨立，又保證了所測模態(tài)動能(平均加速度幅值)較大;有效獨立驅(qū)動點留數(shù)法［12］確定的傳感器位置相對靠近井字梁結(jié)構(gòu)的中間位置，與有效獨立法結(jié)果比較，其中三個傳感器的位置發(fā)生改變，從模態(tài)動能(平均加速度幅值)第三大節(jié)點群轉(zhuǎn)移到了模態(tài)動能(平均加速度幅值)第四大節(jié)點群，模態(tài)動能(平均加速度幅值)進一步降低，傳感器測點主要集中于結(jié)構(gòu)的低階模態(tài);有效獨立驅(qū)動點殘差法［13］確定的傳感器位置更進一步靠近井字梁結(jié)構(gòu)中間位置，與有效獨立法結(jié)果相比，其中四個傳感器的位置從模態(tài)動能(平均加速度幅值)第三大節(jié)點群轉(zhuǎn)移到了模態(tài)動能(平均加速度幅值)第四大節(jié)點群，模態(tài)動能(平均加速度幅值)比有效獨立驅(qū)動點留數(shù)法［12］更進一步降低，傳感器布置結(jié)果已集中于第一階模態(tài)，不利于識別高階模態(tài)，與前文論述的結(jié)果一致。

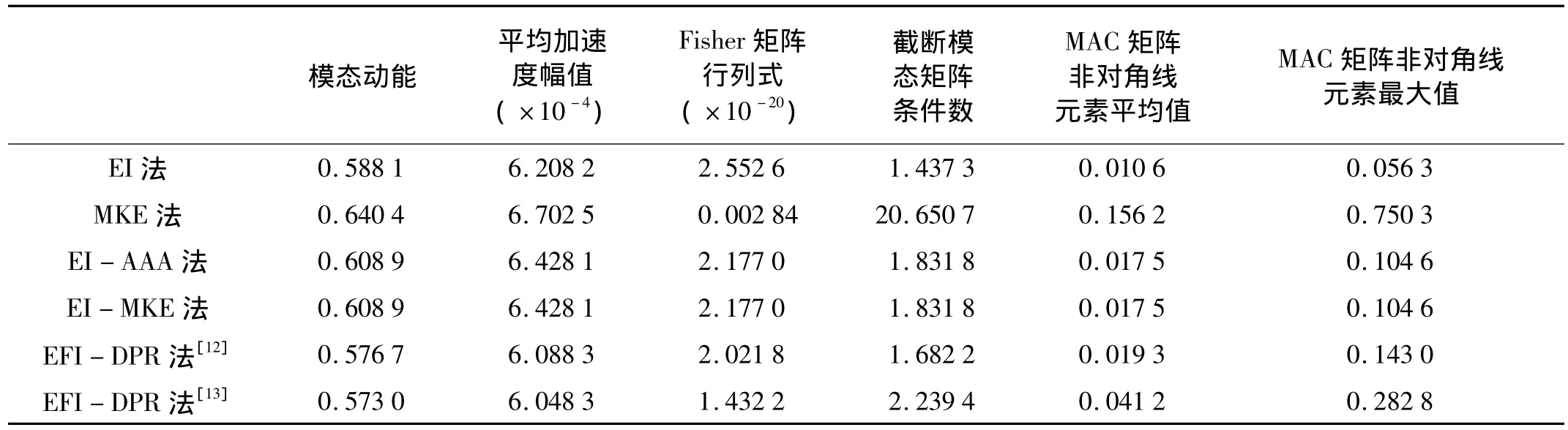
表1 不同方法不同優(yōu)化準則的比較結(jié)果Tab.1 Comparison results of different optimal criterion in different methods

下面通過前文所述的幾種優(yōu)化布置準則對所有方法的有效性進行分析評價，結(jié)果如表1和圖7所示。其中前三個準則與模態(tài)向量的歸一化因子有關(guān)，比較它們的相對大小即可;后三個準則與模態(tài)向量的歸一化因子無關(guān)，可以直接比較它們的絕對大小。本文采用的是質(zhì)量歸一化振型，量級為10-3。

模態(tài)動能和平均加速度幅值準則能保證傳感器布設(shè)在反應(yīng)幅值點，有利于數(shù)據(jù)采集和提高測量抗噪能力。本文所提兩種方法的模態(tài)動能和平均加速度幅值介于有效獨立法和模態(tài)動能法之間，但都大于文獻［12］的有效獨立-驅(qū)動點留數(shù)法和文獻［13］的有效獨立-驅(qū)動點殘差法，說明本文兩種方法的布置測點動態(tài)響應(yīng)要好于有效獨立法、文獻［12-13］的方法。

Fisher信息矩陣行列式是評價測量噪聲對模態(tài)影響的指標，其值越大，試驗測量信號的估計偏差越小，抗噪聲能力越強。有效獨立-平均加速度幅值法和有效獨立-模態(tài)動能法的Fisher信息矩陣行列式介于有效獨立法和模態(tài)動能法之間，但都大于文獻［12］的有效獨立-驅(qū)動點留數(shù)法和文獻［13］的有效獨立-驅(qū)動點殘差法。可見，本文兩種方法布置測點所獲模態(tài)參數(shù)的信息量都好于模態(tài)動能法和文獻［12-13］的方法，但又基本保持了有效獨立法捕獲模態(tài)信息能力強的優(yōu)點。

截斷模態(tài)矩陣條件數(shù)準則是從模態(tài)向量線性獨立性的角度考查所選測點優(yōu)劣的指標。有效獨立-平均加速度幅值法和有效獨立-模態(tài)動能法的截斷模態(tài)矩陣條件數(shù)介于有效獨立法和模態(tài)動能法之間，但又都小于文獻［12］的有效獨立-驅(qū)動點留數(shù)法和文獻［13］的有效獨立-驅(qū)動點殘差法，可見，本文兩種方法獲得的截斷模態(tài)線性獨立性較好。

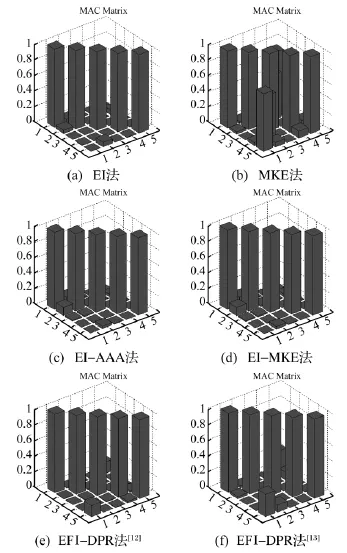
圖7 各種方法的MAC矩陣直方圖Fig.7 MAC matrix histogram of all methods

MAC矩陣非對角線元素平均值和最大值也是評價截斷模態(tài)相關(guān)性的指標。有效獨立-平均加速度幅值法和有效獨立-模態(tài)動能法的MAC矩陣非對角線元素都介于有效獨立法和模態(tài)動能法之間，但都小于文獻［12］的有效獨立-驅(qū)動點留數(shù)法和文獻［13］的有效獨立-驅(qū)動點殘差法，具體可參見圖7。由此可見，有效獨立-平均加速度幅值法和有效獨立-模態(tài)動能法的截斷模態(tài)線性獨立性好于模態(tài)動能法和文獻［12-13］的方法。

通過上述六種準則對傳感器優(yōu)化布置結(jié)果的比較，有效獨立-平均加速度幅值法和有效獨立-模態(tài)動能法在保持截斷模態(tài)最大線性獨立和模態(tài)參數(shù)信息量最大的同時，考慮了能量和平均加速度響應(yīng)的影響，避免了有效獨立法將傳感器布置在低能量部位所造成的信息丟失問題，綜合了二者的優(yōu)點，是這六種方法中最有效可靠的傳感器布置方法。

6 結(jié)論

(1)針對傳統(tǒng)傳感器優(yōu)化布置方法——有效獨立法和模態(tài)動能法的優(yōu)缺點，從多自由度頻響函數(shù)矩陣的模態(tài)展式出發(fā)，推導(dǎo)了平均位移幅值、平均速度幅值和平均加速度幅值的基本公式，分別以平均加速度幅值和模態(tài)動能來修正有效獨立法，提出了兩種改進傳感器優(yōu)化布置方法——有效獨立-平均加速度幅值法(EI-AAA)和有效獨立-模態(tài)動能法(EI-MKE)。同時，提出了平均加速度幅值傳感器評價準則，其能夠保證傳感器布設(shè)在結(jié)構(gòu)響應(yīng)的幅值點，有利于數(shù)據(jù)的采集和提高測量的抗噪能力。

(2)以某實際鋼結(jié)構(gòu)井字梁采光頂結(jié)構(gòu)為算例，運用模態(tài)動能、平均加速度幅值、Fisher信息矩陣行列式、截斷模態(tài)矩陣條件數(shù)、模態(tài)置信準則等六種傳感器優(yōu)化布置方法評價準則，比較了本文所提兩種方法與有效獨立法、模態(tài)動能法、有效獨立-驅(qū)動點留數(shù)法［12］(EFI-DPR)、有效獨立 -驅(qū)動殘差法［13］。數(shù)值分析表明，本文提出的改進傳感器優(yōu)化布置方法——有效獨立-平均加速度幅值法(EI-AAA)和有效獨立-模態(tài)動能法(EI-MKE)，充分結(jié)合有效獨立法和模態(tài)動能法的優(yōu)點，使測點優(yōu)化結(jié)果即能滿足目標模態(tài)保持最大線性獨立又能使測得的模態(tài)動能保持最大，在六種方法中布置結(jié)果最為有效。

［1］劉福強，張令彌.作動器/傳感器優(yōu)化配置的研究進展［J］.力學(xué)進展.2000，30(4):506-516.

LIU Fu-qiang， ZHANG Ling-mi. Advancesinoptimal placement ofactuatorsand sensors［J］. Advancesin Mechanics，2000，30(4):506-516.

［2］ Staszewski W J，Worden K.An overview of optimal sensor location methods for damage detection［C］.Proceedings of SPIE，2001，4326，179-187.

［3］李東升，張 瑩，任 亮，等.結(jié)構(gòu)健康監(jiān)測中的傳感器布置方法及評價準則［J］.力學(xué)進展.2011，41(1):39-50.

LI Dong-sheng，ZHANG Ying，REN Liang，et al.Sensor deploymentfor structural health monitoring and their evaluation［J］.Advances in Mechanics，2011，41(1):39-50.

［4］覃柏英，林賢坤，張令彌，等.基于整數(shù)編碼遺傳算法的傳感器優(yōu)化配置研究［J］.振動與沖擊，2011，30(2):252-257.

QIN Bai-ying， LIN Xian-kun， ZHANG Ling-mi，et al.Optimal sensor placement based on integer-coded genetic algorithm ［J］.Journal of Vibration and Shock，2011，30(2):252-257.

［5］楊雅勛，郝憲武，孫 磊.基于能量系數(shù)-有效獨立法的橋梁結(jié)構(gòu)傳感器優(yōu)化布置［J］.振動與沖擊，2010，29(11):119-123，134.

YANG Ya-xun，HAO Xian-wu，SUN Lei.Optimal placement of sensors for a bridge structure based on energy coefficient effective independence method［J］.Journal of Vibration and Shock，2010，29(11):119-123，134.

［6］Meo M，Zumpano G.On the optimal sensor placement techniques for a bridge structure［J］.Engineering Structures，2005，27:1488-1497.

［7］Liu W，Gao W C，Sun Y，et al.Optimal sensor placement for spatial lattice structure based on genetic algorithms［J］.Journal of Sound and Vibration，2008，317(1-2):175-189.

［8］KammerD C. Sensorplacementforon-orbitmodal identification and correlation of large space structures［J］.Journal of Guidance，Control，and Dynamics，1991，14:251-259.

［9］Kammer D C.Sensor set expansion for modal vibration testing［J］.Mechanical Systems and Signal Processing，2005，19:700-713.

［10］ Papadopoulos M，Garcia E.Sensor placement methodologies for dynamic testing［J］.AIAA Journal，1998，36(2):256-263.

［11］ Li D S，LI H N，F(xiàn)ritzen C P.A note on fast computation of effective independence through QR downdating for sensor placement［J］.Mechanical Systems and Signal Processing，2009，23:1160-1168.

［12］ Imamovic N.Model validation of large finite element model using test data［D］.Imperial College，London，1998.

［13］吳子燕，代鳳娟，宋 靜.損傷檢測中的傳感器優(yōu)化布置方法研究［J］.西北工業(yè)大學(xué)學(xué)報，2007，25(4):503-507.

WU Zi-yan，DAI Feng-jiao，SONG Jing.A more efficient optimalsensorplacementmethod forstructure damage detection［J］. Journal of Northwestern Polytechnical University，2007，25(4):503-507.

［14］劉 偉.空間網(wǎng)格結(jié)構(gòu)健康監(jiān)測系統(tǒng)關(guān)鍵技術(shù)研究［D］.哈爾濱:哈爾濱工業(yè)大學(xué)，2009.