三種湍流模型對(duì)導(dǎo)管螺旋槳空化性能計(jì)算的比較

李 超，周其斗，潘雨村，陶 山

海軍工程大學(xué)艦船工程系，湖北武漢430033

0 引 言

空化是在水力機(jī)械中和高速水下航行體表面經(jīng)常發(fā)生的現(xiàn)象。空化的發(fā)生常常導(dǎo)致水力機(jī)械過(guò)流部件表面嚴(yán)重破壞，并產(chǎn)生強(qiáng)烈的空化噪聲。與此同時(shí)，對(duì)于螺旋槳，還常伴隨著推進(jìn)效率的下降。由于空化測(cè)試成本較高，如何準(zhǔn)確地對(duì)空化流動(dòng)進(jìn)行數(shù)值模擬一直是計(jì)算流體動(dòng)力學(xué)（CFD）領(lǐng)域關(guān)心的問(wèn)題。目前，對(duì)于螺旋槳不考慮空化條件下的性能計(jì)算已經(jīng)比較成熟［1-2］。在近年的研究中，常采用在兩相流模型［3］的基礎(chǔ)上增加空化模型來(lái)進(jìn)行空化模擬。在各種空化模型［4-5］中，Rayleigh-Plesset 空化模型應(yīng)用較廣泛，并獲得了較好的計(jì)算結(jié)果［6］。湍流模型常選擇標(biāo)準(zhǔn)k-ε 模型［7］，錢忠東等［8］對(duì)不同湍流模型對(duì)水翼性能數(shù)值計(jì)算的影響進(jìn)行了對(duì)比分析，但對(duì)不同湍流模型對(duì)螺旋槳空化性能模擬計(jì)算精度的影響缺少必要的研究。

本文將以某單位設(shè)計(jì)的BD12+D4-70 型導(dǎo)管螺旋槳為例，借助通用計(jì)算流體力學(xué)軟件，采用Rayleigh-Plesset 空化模型和3 種不同的湍流模型，對(duì)該槳在3 個(gè)不同空化數(shù)條件下進(jìn)行了數(shù)值模擬，得到在不同湍流模型、不同空化數(shù)條件下導(dǎo)管螺旋槳的空泡性能，并與已有試驗(yàn)數(shù)據(jù)進(jìn)行比對(duì)。同時(shí)，還將分析不同湍流模型、不同空化數(shù)對(duì)槳葉、導(dǎo)管相關(guān)空泡性能計(jì)算的影響，定性的比較3 種湍流模型對(duì)空化數(shù)的敏感程度。

1 數(shù)學(xué)模型

采用Rayleigh-Plesset 空化模型，在該空化模型的控制方程方面，連續(xù)方程為

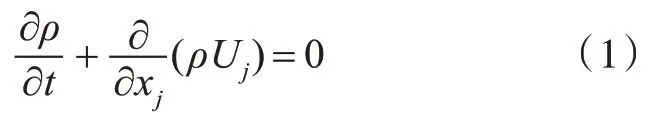
動(dòng)量方程為

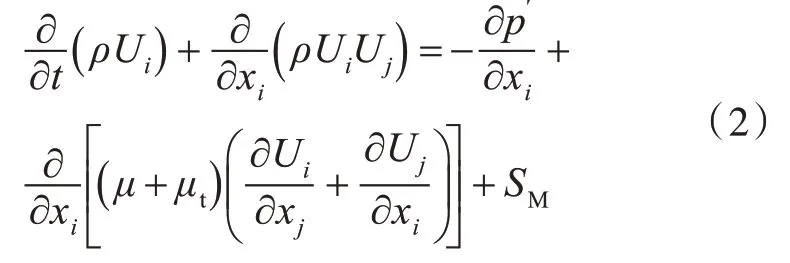
空化過(guò)程描述方程為

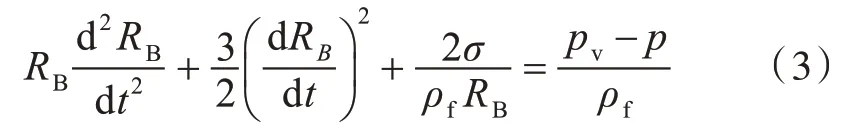
式中：μt為渦粘系數(shù)；SM為流體質(zhì)點(diǎn)所受的質(zhì)量力；RB為氣泡半徑；pv為汽化壓力；p 為環(huán)境壓強(qiáng)；ρf為液體的密度；σ 為氣泡與液體之間的表面張力系數(shù)。

在確定渦粘系數(shù)μt時(shí)，將其與湍流時(shí)均參數(shù)聯(lián)系起來(lái)，即形成湍流模型。本文為了比較不同湍流模型對(duì)空化模擬結(jié)果的影響，分別采用了標(biāo)準(zhǔn)k-ε 模型、RNG k-ε 模型和k-ω 模型。

1.1 標(biāo)準(zhǔn)k-ε 模型

在標(biāo)準(zhǔn)k-ε 模型中，湍動(dòng)能和耗散率的控制方程為

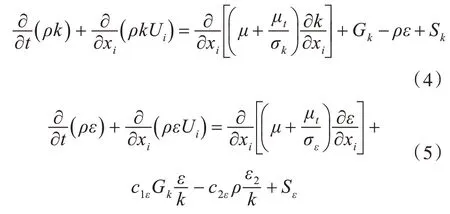
式中：Sk和Sε為用戶自定義的源項(xiàng)；μt為湍流粘性系數(shù)；模型常數(shù)為cμ=0.09，c1=1.44，c2=1.92，σk=1.0，σε=1.3。

1.2 RNG k-ε 模型

RNG k-ε 模型是基于重整化群（Renormaliza?tion Group）的理論提出，經(jīng)改進(jìn)，其控制方程與標(biāo)準(zhǔn)k-ε 模型形式相同，但模型常數(shù)略有差異：cμ=0.085，c2ε=1.68，σk=σε=0.717 9 。主 要 區(qū)別在于，c1不再是常數(shù)，而是表示為η（湍流時(shí)間尺度與平均應(yīng)變率之比）的函數(shù)：

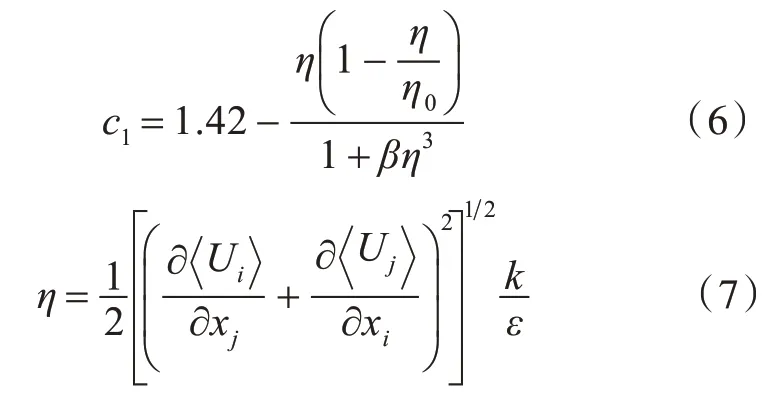
式中，η0=4.38；β=0.015。 RNG k-ε 模型增加了平均應(yīng)變率的影響。

1.3 k-ω 模型

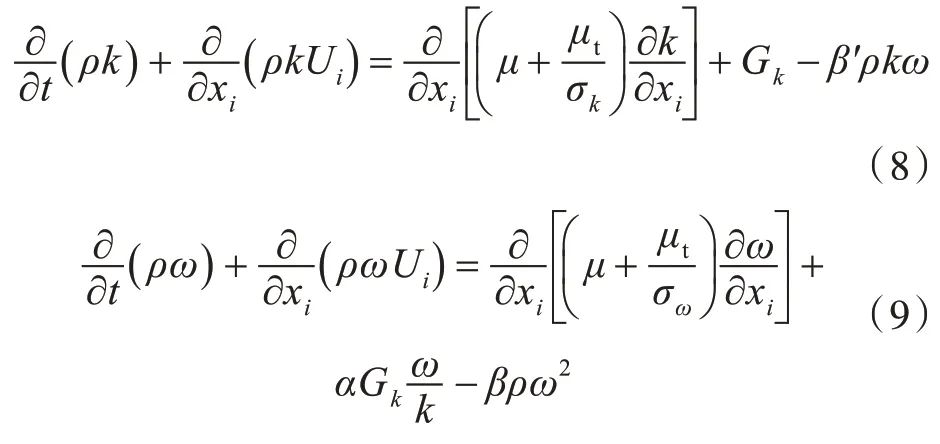
式中：β′=0.09；α=5/9；β=0.075；σk=2；σω=2。

2 計(jì)算模型

本文的具體研究對(duì)象是由某單位設(shè)計(jì)的BD型導(dǎo)管+D 系列螺旋槳。導(dǎo)管的剖面形狀和螺旋槳葉片展開(kāi)輪廓圖如圖1 所示。槳葉直徑為0.24 m，螺距比為1.4，盤(pán)面比為0.7，共有4 片槳葉，導(dǎo)管內(nèi)壁與槳葉葉梢間隙為1.5 mm。

在此基礎(chǔ)上，利用Gambit 對(duì)該導(dǎo)管螺旋槳進(jìn)行了三維建模，如圖2 所示。本文的數(shù)值模擬采用多重參考系MFR 方法，將流域分為靜域和動(dòng)域。螺旋槳所在區(qū)域（區(qū)域1）為動(dòng)域，其余為靜域（區(qū)域2～區(qū)域5）。

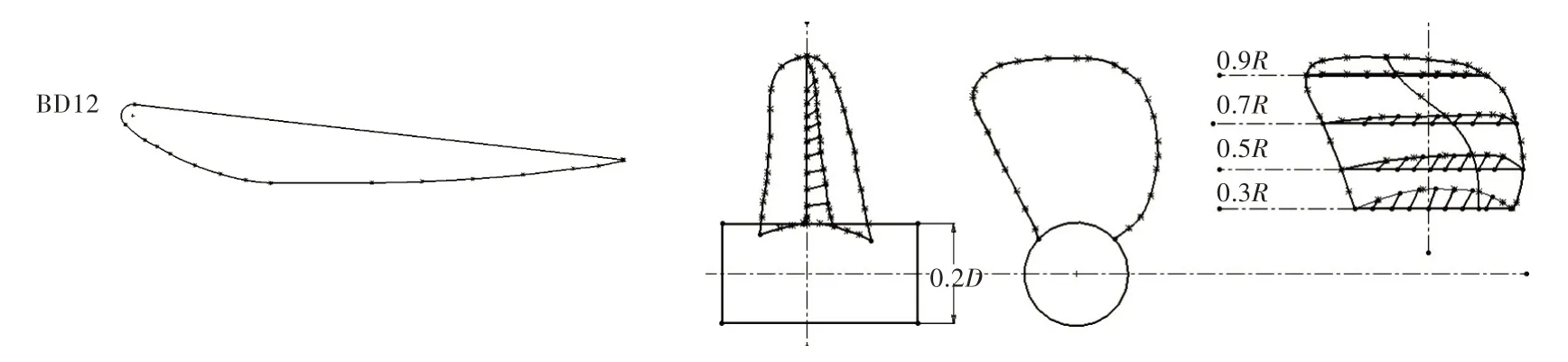
圖1 導(dǎo)管剖面圖和螺旋槳葉片展開(kāi)輪廓Fig.1 Section plane of duct and propeller blade

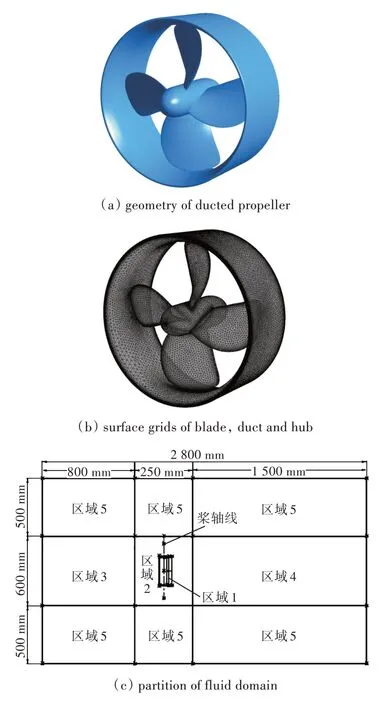
圖2 計(jì)算采用的導(dǎo)管螺旋槳的幾何外形、表面網(wǎng)格和流域劃分Fig.2 Geometry of ducted propeller，surface grids and partitions of fluid domain

導(dǎo)管螺旋槳所在的流域?yàn)橐粋€(gè)長(zhǎng)2.8 m，直徑1.6 m 的圓柱形區(qū)域，流域被分為5 個(gè)部分進(jìn)行網(wǎng)格劃分。由于導(dǎo)管螺旋槳的幾何模型較復(fù)雜，因此，在區(qū)域1 和區(qū)域2 采用適應(yīng)性強(qiáng)的非結(jié)構(gòu)化網(wǎng)格進(jìn)行劃分，而在區(qū)域3～區(qū)域5 則選用六面體單元?jiǎng)澐志W(wǎng)格。此計(jì)算模型共有512 444 個(gè)節(jié)點(diǎn)，2 447 659 個(gè)體單元（其中無(wú)高度傾斜的體單元）。

進(jìn)行數(shù)值計(jì)算時(shí)，均使用相同的邊界條件：進(jìn)口為均勻來(lái)流，入流速度為3 m/s；出口選取CFX中outlet 的static pressure 條件；葉片、導(dǎo)管和槳轂采用無(wú)滑移絕熱壁面條件；遠(yuǎn)場(chǎng)區(qū)域速度與來(lái)流相同；動(dòng)、靜域之間采用CFX 中以GGI 方式連接的Frozen Rotor 參考坐標(biāo)系轉(zhuǎn)換方法。在進(jìn)行空化性能計(jì)算時(shí)，汽化壓力選為25℃時(shí)水的汽化壓力，為3 574 Pa。

3 數(shù)值計(jì)算結(jié)果

由試驗(yàn)圖譜可知，在空化數(shù)為σ =2.4，3.3，4.5這3 種情況下，在進(jìn)速系數(shù)J = 0.6～0.9 時(shí)，空化性能與無(wú)空化的敞水性能相差較大。因此，在進(jìn)行計(jì)算時(shí)，進(jìn)速系數(shù)的選取范圍為0.6～0.9。可通過(guò)保持入流速度不變，調(diào)整螺旋槳轉(zhuǎn)速來(lái)改變進(jìn)速系數(shù)。

3.1 不考慮空化的敞水性能計(jì)算結(jié)果

由于空泡計(jì)算對(duì)計(jì)算的初始值要求較高，因此本文在進(jìn)行數(shù)值模擬時(shí)先不考慮空泡，先采用3 種不同的湍流模型對(duì)導(dǎo)管螺旋槳的敞水性能進(jìn)行計(jì)算，待其收斂后再以此時(shí)的值為初始值，分別用不同的湍流模型進(jìn)行空泡性能計(jì)算。根據(jù)在不考慮空泡情況下的計(jì)算結(jié)果，得出在J = 0.6，0.7，0.8，0.9 處的敞水性能KT，KQ，η 與試驗(yàn)所得的敞水性能曲線對(duì)比如圖3 所示。

3 種不同湍流模型計(jì)算的相對(duì)誤差如表1 所示。由表中可看出，推力系數(shù)KT、扭矩系數(shù)KQ及推進(jìn)效率η 的計(jì)算結(jié)果誤差均約為5%，滿足工程預(yù)報(bào)的要求，同時(shí)，也證明了采用數(shù)值模擬計(jì)算導(dǎo)管螺旋槳敞水性能的可靠性。

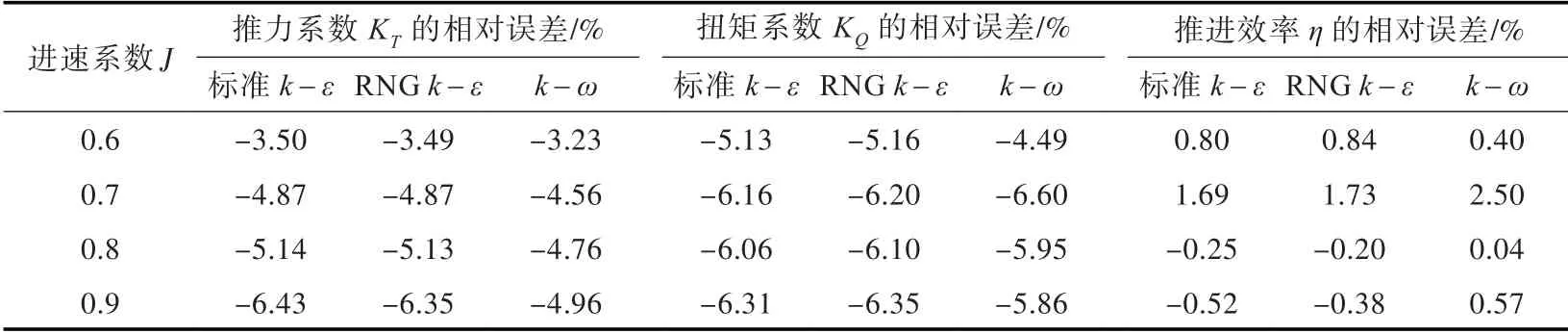
表1 3 種不同湍流模型計(jì)算的相對(duì)誤差Tab.1 Calculation errors of different turbulence models

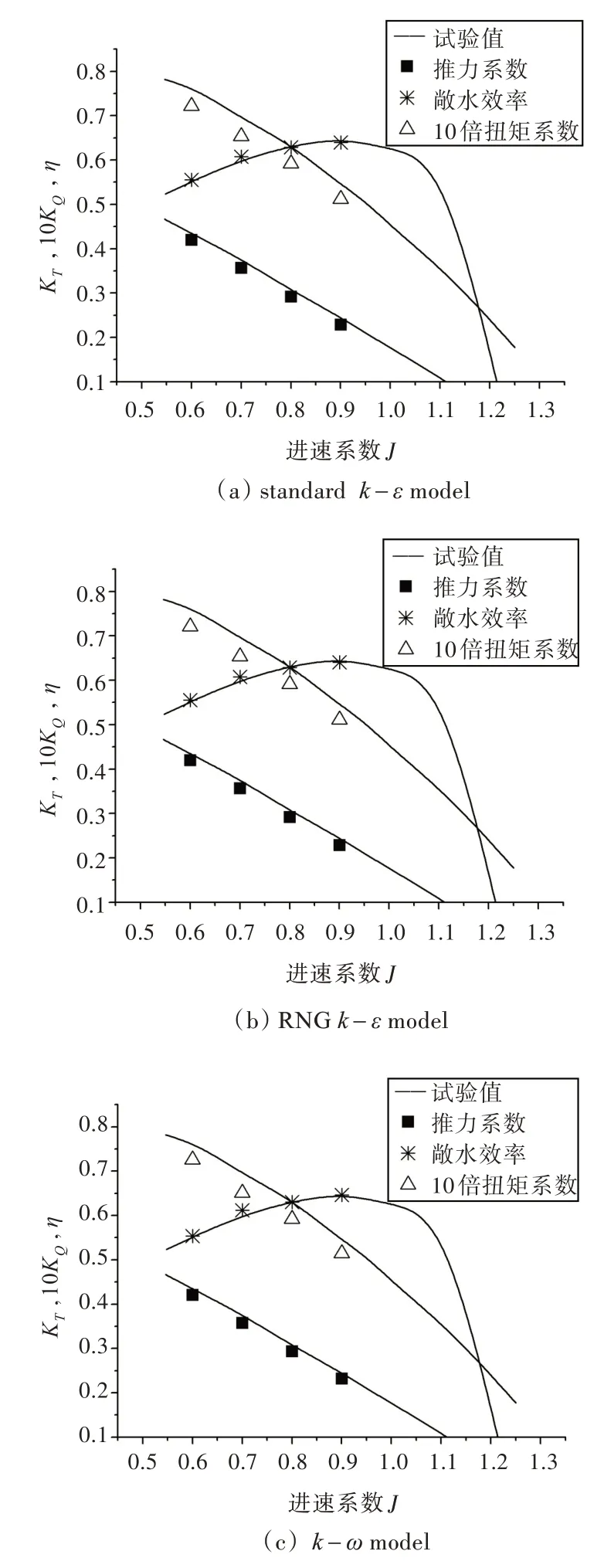
圖3 不同湍流模型的敞水性能計(jì)算結(jié)果Fig.3 Open water performance calculated by different turbulence models

3.2 不同空化數(shù)下的空泡性能計(jì)算結(jié)果

空化數(shù)σ 是空化流動(dòng)的一個(gè)重要參數(shù)，直接影響著空泡的大小及空化發(fā)生的位置，進(jìn)而影響到空化性能。本文對(duì)空化數(shù)σ = 2.4，3.3，4.5 這3種不同的情況進(jìn)行了空泡性能計(jì)算。在定義出口為static pressure 條件時(shí)，輸入的相對(duì)壓力即為遠(yuǎn)場(chǎng)的環(huán)境壓力，空化數(shù)的調(diào)整是通過(guò)改變此環(huán)境壓力來(lái)實(shí)現(xiàn)的。計(jì)算結(jié)果與試驗(yàn)數(shù)據(jù)的對(duì)比如圖4～圖6 所示。

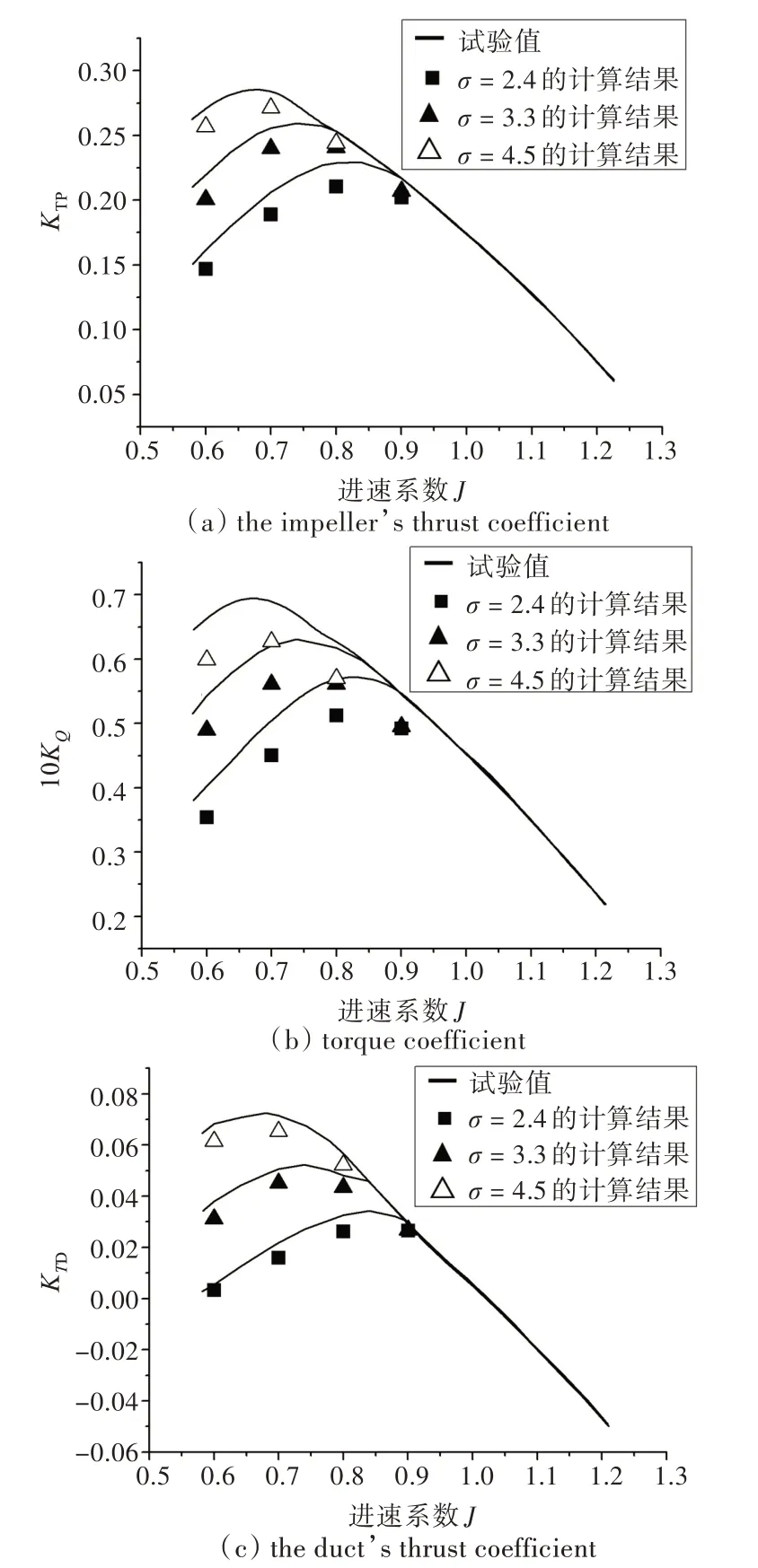
圖4 標(biāo)準(zhǔn)k-ε 湍流模型的空泡性能計(jì)算結(jié)果Fig.4 Cavitation performance calculated by standard k-ε model

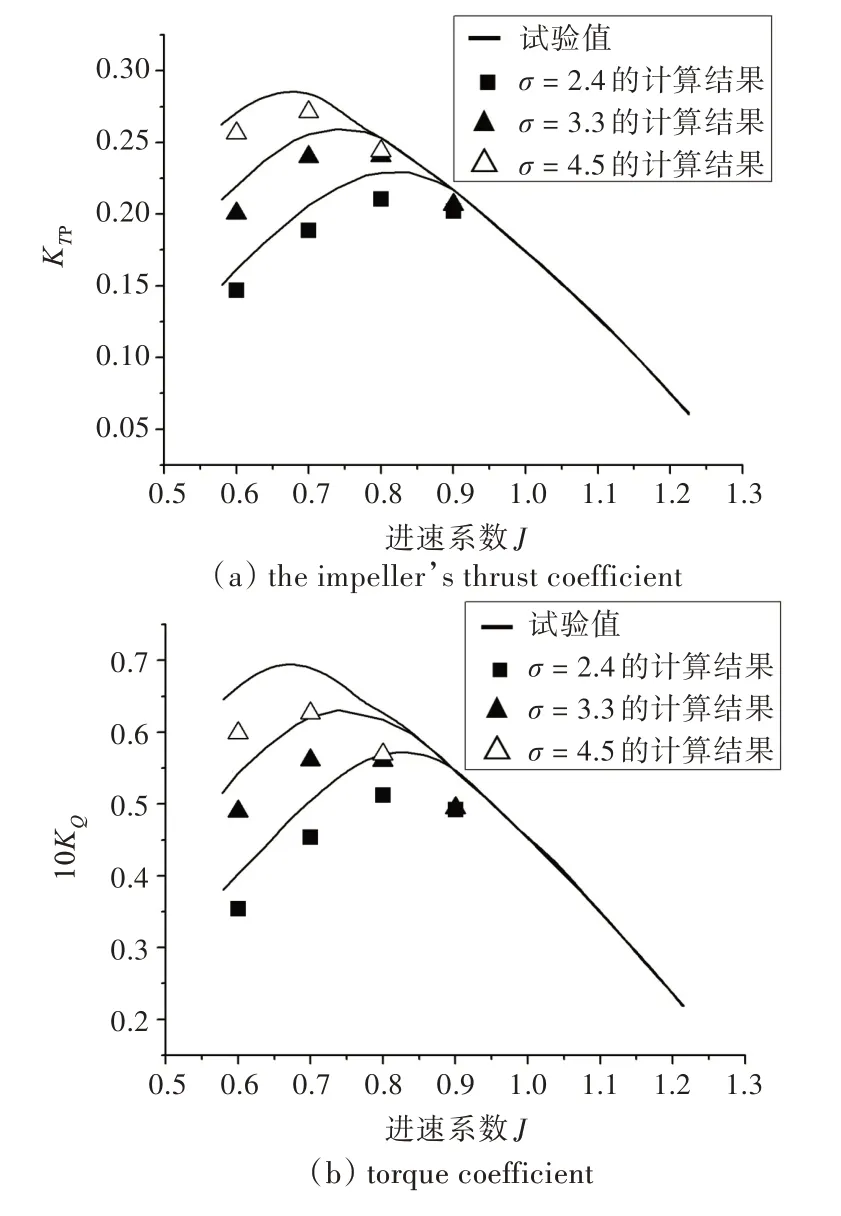
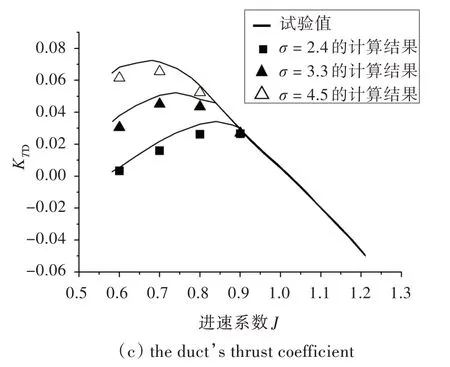
圖5 RNG k-ε 湍流模型的空泡性能計(jì)算結(jié)果Fig.5 Cavitation performance calculated by RNG k-ε model

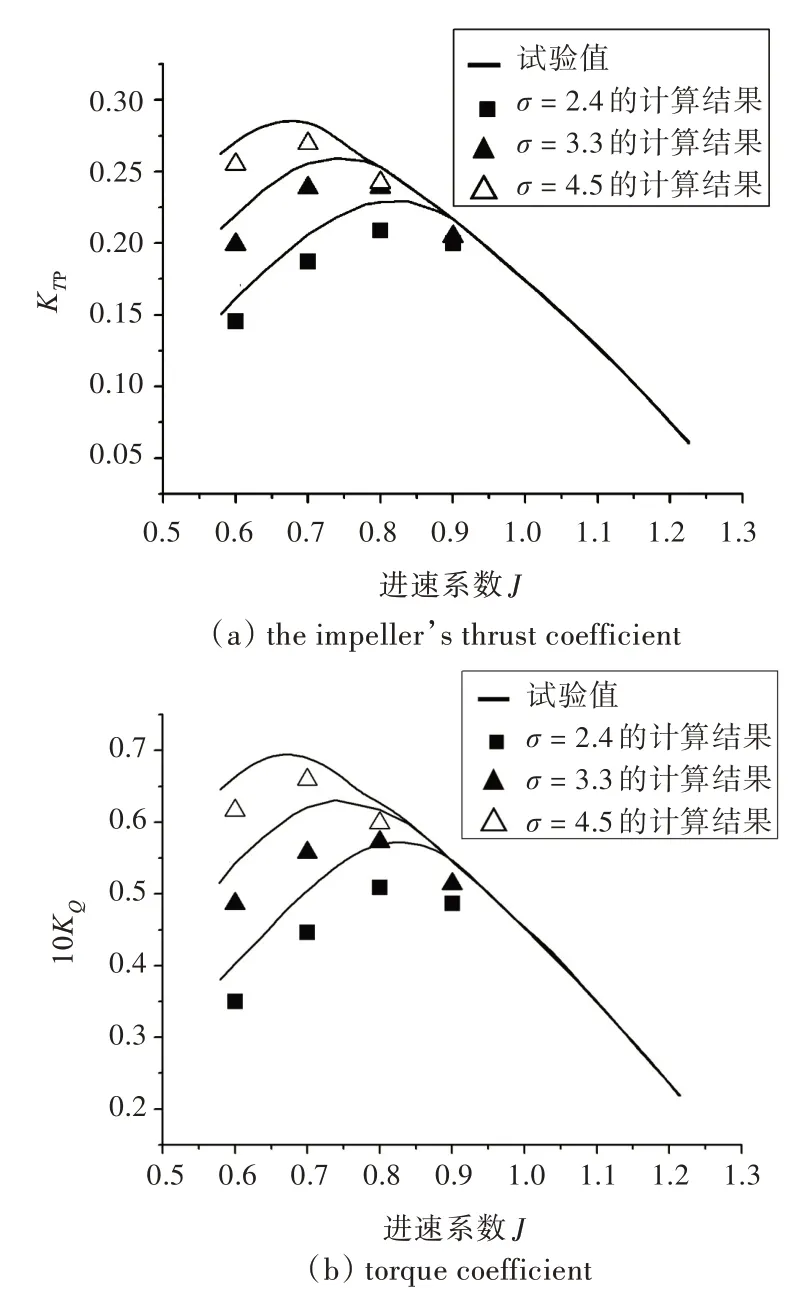
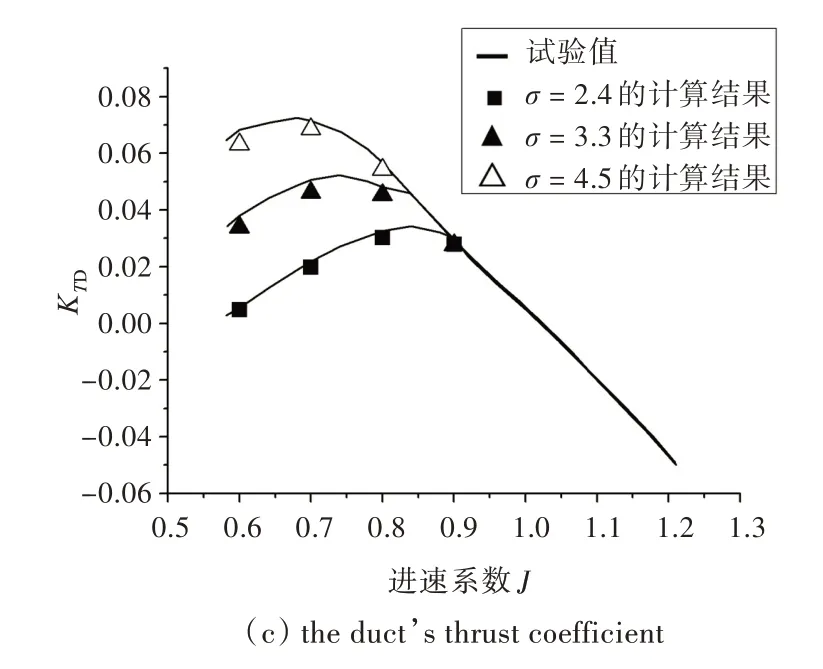
圖6 k-ω 湍流模型的空泡性能計(jì)算結(jié)果Fig.6 Cavitation performance calculated by k-ω model

4 計(jì)算結(jié)果對(duì)比與分析

4.1 相同空化數(shù)不同湍流模型的計(jì)算結(jié)果比較分析

在相同空化數(shù)條件下，對(duì)不同湍流模型計(jì)算結(jié)果的相對(duì)誤差進(jìn)行了比較，如表2 所示（以σ =3.3 為例，其他空化數(shù)條件下的規(guī)律相似）。由表中數(shù)據(jù)可知，標(biāo)準(zhǔn)k-ε 模型與RNG k-ε 模型的計(jì)算結(jié)果相當(dāng)接近；在計(jì)算槳葉的推力系數(shù)KTP和扭矩系數(shù)KQ時(shí)，k-ω 模型相比其他兩種模型計(jì)算誤差稍大，但仍在允許范圍內(nèi)，推進(jìn)效率η 的計(jì)算誤差均在5%以內(nèi)，符合工程預(yù)報(bào)的要求。

另外，從表中還可以看到，隨著進(jìn)速系數(shù)的增大，誤差逐漸減小。尤其是在計(jì)算扭矩系數(shù)時(shí)，當(dāng)J ＜0.8 時(shí)，相對(duì)誤差較大，最大達(dá)到了10%以上（k-ω 模型，J = 0.6 時(shí)），而當(dāng)J = 0.9 時(shí)，相對(duì)誤差則明顯較小。

表2 σ =3.3 時(shí)3 種不同湍流模型計(jì)算的相對(duì)誤差Tab.2 Calculation errors of different turbulence models at σ =3.3

在計(jì)算過(guò)程中，發(fā)現(xiàn)相對(duì)于另外兩種模型而言，k-ω 模型計(jì)算所用時(shí)間更短，并且更加容易收斂。這種情況與文獻(xiàn)［1］中計(jì)算螺旋槳敞水性能時(shí)的情況相似。

另外，對(duì)于導(dǎo)管螺旋槳的數(shù)值計(jì)算，還要考察導(dǎo)管推力系數(shù)的計(jì)算結(jié)果。同樣以σ =3.3 時(shí)的情況為例，3 種湍流模型的導(dǎo)管推力系數(shù)的計(jì)算結(jié)果相對(duì)誤差如表3 所示。由表中數(shù)據(jù)可以看出，在進(jìn)速系數(shù)較低時(shí)，如J =0.6，0.7 時(shí)，標(biāo)準(zhǔn)k-ε 模型與RNG k-ε 模型的計(jì)算結(jié)果嚴(yán)重失真，誤差最大接近20%（RNG k-ε 模型，J =0.6時(shí)），而k-ω 模型的計(jì)算結(jié)果則比較穩(wěn)定，始終控制在10%左右。

綜合以上情況可知，k-ω 模型更適于導(dǎo)管螺旋槳空化性能的計(jì)算。

4.2 相同湍流模型不同空化數(shù)的計(jì)算結(jié)果比較分析

同一種湍流模型在不同空化數(shù)條件下的計(jì)算精度并不相同。其中，k-ω 模型對(duì)于不同空化數(shù)的計(jì)算精度如表4 所示，其余兩個(gè)模型的規(guī)律與之相似。由表4 可以發(fā)現(xiàn)，σ = 2.4 時(shí)的計(jì)算精度最差，隨著空化數(shù)的增大，計(jì)算精度隨之上升。眾所周知，在較低的空化數(shù)條件下，空化的發(fā)生與發(fā)展均相對(duì)較劇烈；在較低的進(jìn)速系數(shù)（σ ＜0.7）下，槳葉推力系數(shù)的計(jì)算精度仍在10%以內(nèi)，而扭矩系數(shù)KQ的計(jì)算精度則較差，相對(duì)誤差最大達(dá)到13%（σ = 2.4，J = 0.6 時(shí)）。進(jìn)速系數(shù)的減小，相當(dāng)于入流速度不變，螺旋槳轉(zhuǎn)速增加，從而導(dǎo)致螺旋槳的空化愈發(fā)劇烈。以上兩種情況可以總結(jié)為，當(dāng)空化較劇烈時(shí)，數(shù)值計(jì)算精度將會(huì)下降，其原因可以歸結(jié)為兩點(diǎn)：一是本文選用的Ray?leigh-Plesset 空化模型是一種簡(jiǎn)化的空化模型，對(duì)于比較劇烈、復(fù)雜的空化，模型失真比較大，從而造成計(jì)算精度的下降；二是當(dāng)空化發(fā)生劇烈時(shí)，對(duì)網(wǎng)格質(zhì)量的要求也進(jìn)一步提高了，但原有的網(wǎng)格并沒(méi)有相應(yīng)改進(jìn)，從而造成計(jì)算精度下降。

同樣，仍以k-ω 模型為例考察導(dǎo)管推力系數(shù)的計(jì)算精度。不同空化數(shù)條件下的計(jì)算相對(duì)誤差如表5 所示。由表中可以看出，當(dāng)σ = 2.4時(shí)，計(jì)算結(jié)果誤差較大，隨著空化數(shù)的增大，誤差逐漸降低。這種情況同樣可以用上面所述的兩點(diǎn)原因解釋。

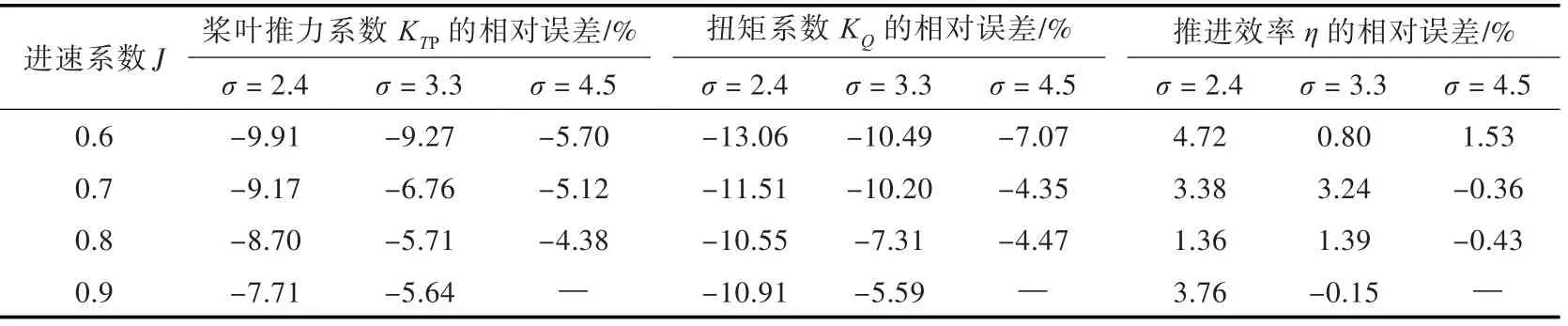
表4 k-ω 湍流模型不同空化數(shù)下數(shù)值計(jì)算相對(duì)誤差Tab.4 Calculation errors of k-ω turbulence model at different cavitation numbers

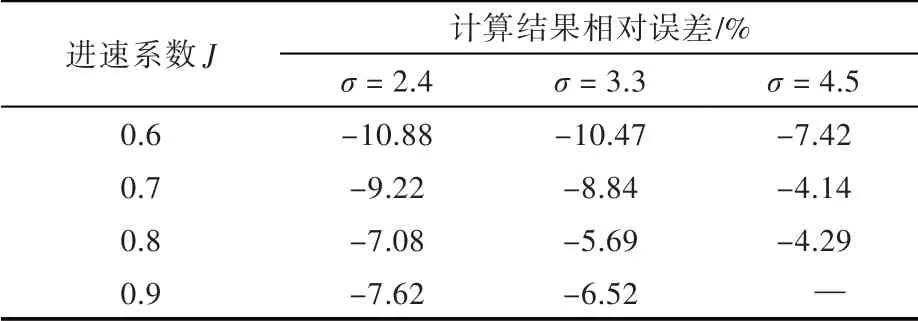
表5 不同空化數(shù)下k-ω 模型計(jì)算導(dǎo)管推力系數(shù)的相對(duì)誤差Tab.5 Calculation errors of duct's thrust coefficient by k-ω turbulence model at different cavitation numbers

4.3 不同湍流模型對(duì)空化數(shù)的敏感性

不同的湍流模型對(duì)空化數(shù)的敏感程度不同。以進(jìn)速系數(shù)J = 0.7 為例，槳葉推力系數(shù)與扭矩系數(shù)的計(jì)算相對(duì)誤差的浮動(dòng)情況如圖7 所示。由圖中可以看出，在計(jì)算槳葉推力系數(shù)時(shí)，在不同空化數(shù)條件下，3 種模型計(jì)算的相對(duì)誤差波動(dòng)相似，但在扭矩系數(shù)的計(jì)算中，k-ω 模型的計(jì)算相對(duì)誤差隨空化數(shù)的改變而變化較大。這說(shuō)明k-ω 模型對(duì)空化數(shù)比較敏感。因此，對(duì)于不同的空化數(shù)，計(jì)算精度相差會(huì)較大。相比k-ω 模型，k-ε 模型和RNG k-ε 模型對(duì)空化數(shù)不敏感，對(duì)于不同的空化數(shù)，計(jì)算時(shí)，計(jì)算精度相差較小。

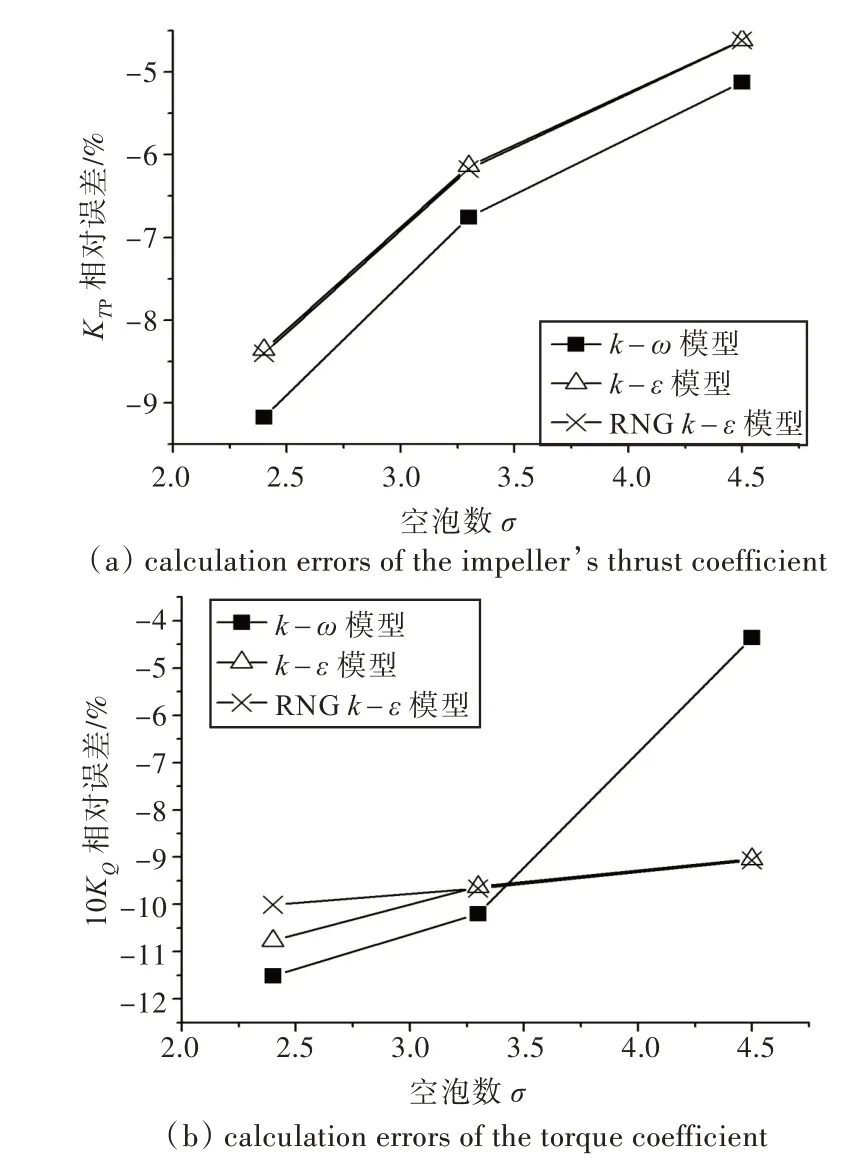
圖7 J =0.7 時(shí)不同湍流模型計(jì)算相對(duì)誤差波動(dòng)Fig.7 The variation of calculation errors of different turbulence models at J =0.7

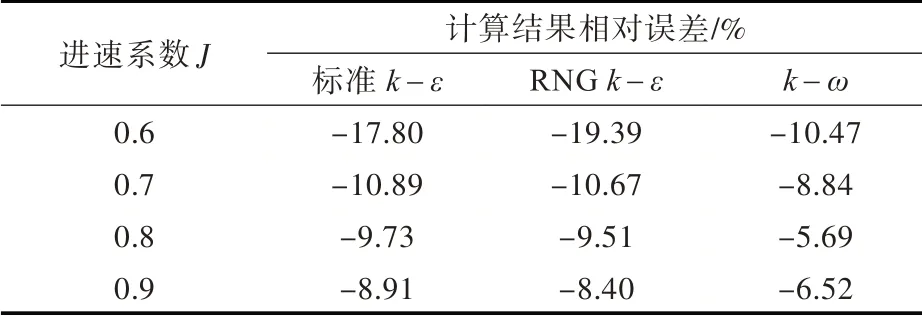
表3 σ =3.3 時(shí)3 種不同湍流模型計(jì)算導(dǎo)管推力系數(shù)的相對(duì)誤差Tab.3 Calculation errors of duct's thrust coefficent by different turbulence models at σ =3.3

5 結(jié) 論

本文借助于CFD 軟件，采用結(jié)構(gòu)化與非結(jié)構(gòu)化網(wǎng)格相結(jié)合的方法，對(duì)導(dǎo)管螺旋槳的空泡性能進(jìn)行了數(shù)值模擬，對(duì)比分析了不同湍流模型、不同空化數(shù)條件下的計(jì)算結(jié)果精度，得出以下結(jié)論：

1）在對(duì)導(dǎo)管螺旋槳進(jìn)行不考慮空化的敞水性能計(jì)算時(shí)，3 種湍流模型的計(jì)算精度均較好，滿足工程預(yù)報(bào)的精度要求。

2）對(duì)導(dǎo)管螺旋槳進(jìn)行空化性能計(jì)算時(shí)，標(biāo)準(zhǔn)k-ω 模型更加穩(wěn)定，計(jì)算所用時(shí)間更短，且更加容易收斂。但對(duì)于槳葉推力系數(shù)的計(jì)算，k-ω 模型的計(jì)算精度不及標(biāo)準(zhǔn)k-ε 模型與RNG k-ε 模型，但是三者的計(jì)算相對(duì)誤差都在允許范圍內(nèi)。在對(duì)導(dǎo)管推力系數(shù)的計(jì)算中，尤其是在低進(jìn)速系數(shù)下，標(biāo)準(zhǔn)k-ε 模型和RNG k-ε 模型嚴(yán)重失真，但是k-ω 模型的計(jì)算精度仍然能夠得到保證。綜合以上情況，k-ω 模型相比標(biāo)準(zhǔn)k-ε 模型和RNG k-ε 模型更加適合導(dǎo)管螺旋槳的空化性能計(jì)算。

3）在空化數(shù)或進(jìn)速系數(shù)較低時(shí)，空化的發(fā)生相對(duì)來(lái)說(shuō)會(huì)較劇烈，在這種情況下進(jìn)行空泡性能的計(jì)算計(jì)算精度不理想。若想提高精度，需要選取更為精確的空化模型，或進(jìn)一步調(diào)整網(wǎng)格，提高網(wǎng)格質(zhì)量。

4）在不同空化數(shù)條件下，標(biāo)準(zhǔn)k-ε 模型與RNG k-ε 模型計(jì)算的相對(duì)誤差波動(dòng)較小，而k-ω模型則較大。這說(shuō)明在計(jì)算時(shí)，k-ω 模型對(duì)空化數(shù)σ 比較敏感。

［1］呂曉軍，周其斗，紀(jì)剛，等.導(dǎo)管螺旋槳敞水性能的預(yù)報(bào)和比較［J］. 海軍工程大學(xué)學(xué)報(bào)，2010，22（1）：24-30.LV Xiaojun，ZHOU Qidou，JI Gang，et al. Prediction and comparison of open water performance of ducted propeller［J］. Journal of Naval University of Engineer?ing，2010，22（1）：24-30.

［2］曾文德，王永生，劉承江. 混流式噴水推進(jìn)器水動(dòng)力性能的數(shù)字模擬［J］. 武漢理工大學(xué)學(xué)報(bào)，2010，32（6）：95-100.ZENG Wende，WANG Yongsheng，LIU Chengjiang.Numerical simulation of hydrodynamic performance of the mixed flow pump for marine waterjet propulsion［J］. Journal of Wuhan University of Technology，2010，32（6）：95-100.

［3］YAN Weicheng，SHI Depan，LUO Zhenghong，et al.Three-dimensional CFD study of liquid-solid flow be?haviors in tubular loop polymerization reactors：The ef?fect of guide vane［J］. Chemical Engineering Science，2011，66（18）：4127-4137.

［4］楊瓊方，王永生，張志宏. 螺旋槳空化崩潰性能圖譜的多相流模擬［J］. 華中科技大學(xué)學(xué)報(bào)（自然科學(xué)版），2012，40（2）：18-22.YANG Qiongfang，WANG Yongsheng，ZHANG Zhi?hong. Multiphase flow simulation and propeller cavita?tion breakdown performance maps［J］. Journal of Hua?zhong University of Science and Technology（Nature Science），2012，40（2）：18-22.

［5］楊瓊方，王永生，張志宏. 非均勻進(jìn)流對(duì)螺旋槳空化水動(dòng)力性能的影響［J］.水動(dòng)力學(xué)研究與進(jìn)展，2011，26（5）：538-550.YANG Qiongfang，WANG Yongsheng，ZHANG Zhi?hong.Effects of non-uniform inflow on propeller cavita?tion hydrodynamics［J］. Chinese Journal of Hydrody?namics，2011，26（5）：538-550.

［6］楊正軍，王福軍，劉竹青，等. 基于CFD 的軸流泵空化特性預(yù)測(cè)［J］. 排灌機(jī)械工程學(xué)報(bào)，2011，29（1）：11-15.YANG Zhengjun，WANG Fujun，LIU Zhuqing，et al.Prediction of cavitation performance of axial-flow pump based on CFD［J］. Drainage and Irrigation Ma?chinery，2011，29（1）：11-15.

［7］余云超，張偉，陳紅勛. 軸流泵模型汽蝕特性的數(shù)值模擬［J］.上海大學(xué)學(xué)報(bào)（自然科學(xué)版），2011，17（5）：653-656.YU Yunchao，ZHANG Wei，CHEN Hongxun. Numeri?cal simulation of cavitation behavior of axial pump mod?el［J］. Journal of Shanghai University（Natural Sci?ence），2011，17（5）：653-656.

［8］錢忠東，黃社華.四種湍流模型對(duì)空化流動(dòng)模擬的比較［J］.水科學(xué)進(jìn)展，2006，17（2）：203-208.QIAN Zhongdong，HUANG Shehua. Comparison and analysis of computed results for cavitating flow with four turbulence mode［J］. Advances In Water Science，2006，17（2）：203-208.