基于受體模型和地統計學相結合的土壤鎘污染源解析

瞿明凱,李衛東,張傳榮,黃 標,胡文友

(1.華中農業大學資源與環境學院資源環境信息系,湖北 武漢 430070；2.中國科學院南京土壤研究所土壤環境與污染修復重點實驗室,江蘇 南京 210008；3.康涅狄格大學地理系,美國康涅狄格州 斯托斯市 06269)

分析污染物的來源以及污染狀況可以為后續的治理和修復提供必要的依據.研究者對污染源的解析存在兩種層次,一種僅僅是定性判斷主要的污染物來源類型,即源識別;另一種不但定性判斷主要的污染源類型,而且定量計算各污染源的貢獻量,即源解析[1].很多研究人員把兩者統稱為源解析.源解析方法起源于大氣環境研究,所用模型主要有兩種.一種是以污染源為研究對象的擴散模型.該模型根據各個污染源的排放量、研究區域與排放源的水平與垂直距離、污染物的理化性質,以及風速風向、湍流等環境因素來計算各個源對研究區域的影響程度.源排放清單是擴散模型必要的輸入數據.Budiansky[2]于1980年指出擴散模型輸入數據的不準確性是其預測誤差的主要來源,而由于排放源清單存在很大的不準確性,模型的預測效果不能使人信服.另一種是以污染區域為研究對象的受體模型[3].該模型著眼于研究排放源對受體(即受到排放源影響的局部環境介質)的貢獻.受體模型通過測量排放源和受體樣品的物理、化學性質,定性識別對受體有貢獻的污染源并定量計算各污染源的分擔率.同時該類模型不依賴于排放源的排放條件、氣象、地形等數據,不追蹤污染物的遷移過程,避開了擴散模型遇到的困難.受體模型是近年來得到廣泛應用的一類方法,常用的受體模型方法有化學質量平衡模型(CMB)、主成分分析/絕對主成分分數(PCA/APCS)、正定矩陣因子分解(PMF)等[4-8].PCA/APCS受體模型首先通過使用PCA得到歸一化的重金屬濃度的因子分數 APCS,再用重金屬濃度數據對APCS做多元線性回歸得到相應的回歸系數.該回歸系數可將APCS轉化為每個污染源對每個樣本的濃度貢獻.PCA/APCS不需要事先了解源的個數及其特點,因此該模型被廣泛應用于源解析研究中[5-8].土壤環境介質污染物源解析的研究起步較晚,目前對土壤重金屬污染源進行定量解析的研究還鮮有報道.PCA的結果與源貢獻相關,但是并不成比例,故其結果只能定性的推測潛在的污染源而不能直接用于源解析[9].應用PCA/APCS受體模型不但可以定量地確定每個變量對每個源的載荷,還可以定量確定源對其重金屬的平均貢獻量和在每個采樣點的貢獻量.但受體模型源解析的結果仍缺乏直觀視覺效果,不利于在源未知的情況下利用源解析結果進行源識別(如隱蔽性污染源).

地統計學方法早已被廣泛應用于插值土壤重金屬含量的空間樣本數據,從有限樣本對土壤重金屬含量的空間分布進行數字制圖[10].但地統計學方法在土壤污染源解析、特別是重金屬污染源解析方面的應用還十分少見,僅在近兩三年出現了一些趨勢和初步應用.Wang等[11]把克里格插值、主成份分析、和線性回歸結合起來研究了土壤中多環芳烴的分布和來源.Davis等[12]結合主成份分析和克里格插值研究了土壤中有毒金屬的來源問題.Schaefer等[13]進而提出了一個結合地統計學和多變量統計分析的土壤金屬元素源解析的雜和方法.但該法主要致力于土壤金屬原始測定數據的地統計學分析,并沒有對具體金屬元素的源貢獻進行制圖和分析.Mostert等[9]就化學計量學在土壤污染分析上的應用情況作了綜述,其中包含受體模型和地統計學方法的在土壤污染分析上應用情況.

為了直觀理解每個 Cd源的貢獻量空間分布和在源未知的情況下推測具體的污染源,本文將地統計學和受體模型結合起來,利用普通克里格法插值由PCA/APCS受體模型獲得的采樣點的源貢獻量.因此該研究的目的是提出一個土壤重金屬污染源解析的綜合方法,并以武漢東湖高新技術開發區的 Cd污染解析為例加以展示.具體步驟為:1.探測采樣數據集的結構,理解潛在因子的實際意義.2.利用PCA/APCS受體模型定量解析 Cd污染源對該研究區域內的貢獻.3.利用地統計學插值得到Cd含量及Cd源貢獻量的空間分布.4.結合 PCA分析結果、Cd含量和 Cd源源貢獻量空間分布圖推測隱性污染源.

1 材料與方法

1.1 研究區概況

研 究 區 域 (114.332～114.481°E,30.394～30.513°N)位于湖北省武漢市東湖高新技術開發區,面積約為150km2,海拔14～65m,年平均溫度為15.9℃,年降雨量為 1,300mm,屬于典型的亞熱帶濕潤季風氣候區.該區域內西北部靠近市中心的區域多為建筑用地,中部涉及電子方面的工廠較為集中,其他部分土地利用類型多為待建用地或者農田.

1.2 數據來源

本研究中樣點采取隨機布設,采樣時用GPS對每一個采樣點精確定位,共計 135個(圖1),采樣時間為 2009年9月.每個樣點取表層土壤 (0～20cm)1kg,棄去動植物殘留體、礫石等雜質,混勻風干后過 100目篩.土壤樣品的化學分析項目按照 GB15618-1995[14]執行完成,主要包括9種土壤金屬元素Ca、Cd、Cu、Fe、Mg、Mn、Ni、Pb、Zn.本研究源解析的對象為呈明顯污染的 Cd元素,其他元素則作為相關信息為Cd源解析服務.Cr因缺乏與Cd和其他元素的相關性而未利用.Hg等元素因故未測,但對于本研究影響不大.

圖1 采樣點分布Fig.1 Distribution of soil sample sites

1.3 主成分分析/絕對主成分分數(PCA/APCS)受體模型

主成分分析(PCA)是對一組變量降維的統計學方法,它包括奇異值的分解(SDV)、維數的選擇(選取主成分)和旋轉(使因子更具有代表性)3個步驟.對 9種土壤中金屬元素(Ca、Cd、Cu、Fe、Mg、Mn、Ni、Pb、Zn)的全量含量進行主成分分析.采用 varimax旋轉來得到有意義的因子.并采用kaiser標準(特征值大于1)來決定合適的因子數目[15].更多有關 PCA的細節,詳見Thurston 等[16]和 Miller等[17]的詳細介紹.

絕對主成分分數(APCS)被用于估計源對重金屬的貢獻量.該技術被廣泛用于大氣科學[18-19]和水文學[20]上.主要步驟為:首先對所有金屬元素含量進行標準化,如下式所示:

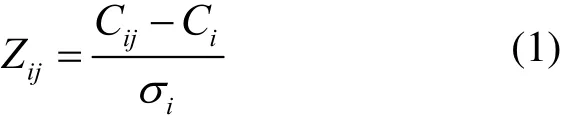
式中:Zij為標準化后的濃度值(無量綱);和σi分別為元素i的平均濃度和標準偏差.從PCA得到的是歸一化的因子分數,即均值為 0和標準偏差為 1.這樣,對所有元素引入一個濃度為 0的人為樣本,可計算得到該0濃度樣本的因子分數為:

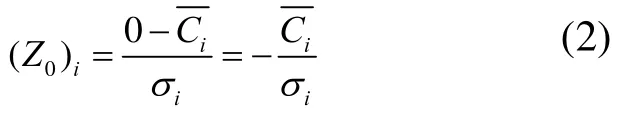
通過使用PCA可得到這些歸一化的重金屬濃度的因子分數.每個重金屬元素的 APCS可由每個樣本的因子分數減去 0濃度樣本的因子分數而得到.再用金屬濃度數據對 APCS做多元線性回歸可得相應的回歸系數.該回歸系數可將APCS轉化為每個污染源對每個樣本的濃度貢獻.對Ci的源貢獻量可由一個多元線性回歸得到,相應公式為:

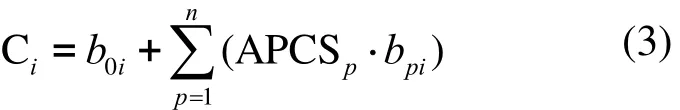
其式中:b0i為對金屬元素i做多元線性回歸所得的常數項.bpi是源p對金屬元素i的回歸系數.APCSp為調整后的因子p的分數.APCSp·bpi表示源p對Ci的質量濃度貢獻,所有樣本的APCSp·bpi的平均值就表示了源平均絕對貢獻量.更多APCS的詳細介紹見文獻[16].

1.4 地統計學分析

地統計學結合采樣點間的空間相關性來預測未采樣點的值.該方法使估計誤差的方差達到最小化,同時極大地減小了調查損失[21].采用普通克里格(OK)來預測Cd及Cd的源貢獻量的空間分布.OK為待估點x0周圍觀測點的線性權重平均,其公式為:

式中:(x0)為位置x0處的預測值;y(xi) 為xi的土壤屬性觀測值,λi為從OK公式系統所得到的對應于觀測值的權重系數,同時為鄰域內觀測樣本的數目.更多OK的詳細介紹見文獻[10].

1.5 數據處理

土壤金屬元素濃度數據的描述性統計、主成份分析和多元線性回歸分析采用SPSS?(version 13)軟件,地統計學分析和空間分布圖的制作通過ArcGIS (version 9.2)來完成.

2 結果與討論

2.1 Cd源解析

如表1所示,該研究區域中重金屬元素Cd的均值(0.74mg/kg)為其背景值的 4.36倍,接近土壤環境質量三級標準(1.00mg/kg)[14],其他重金屬元素均值接近背景值水平,顯示Cd可能受到人類活動的強烈影響.由于本文所用的背景值為湖北省背景值,可能與原地實際背景值(缺)有些出入.

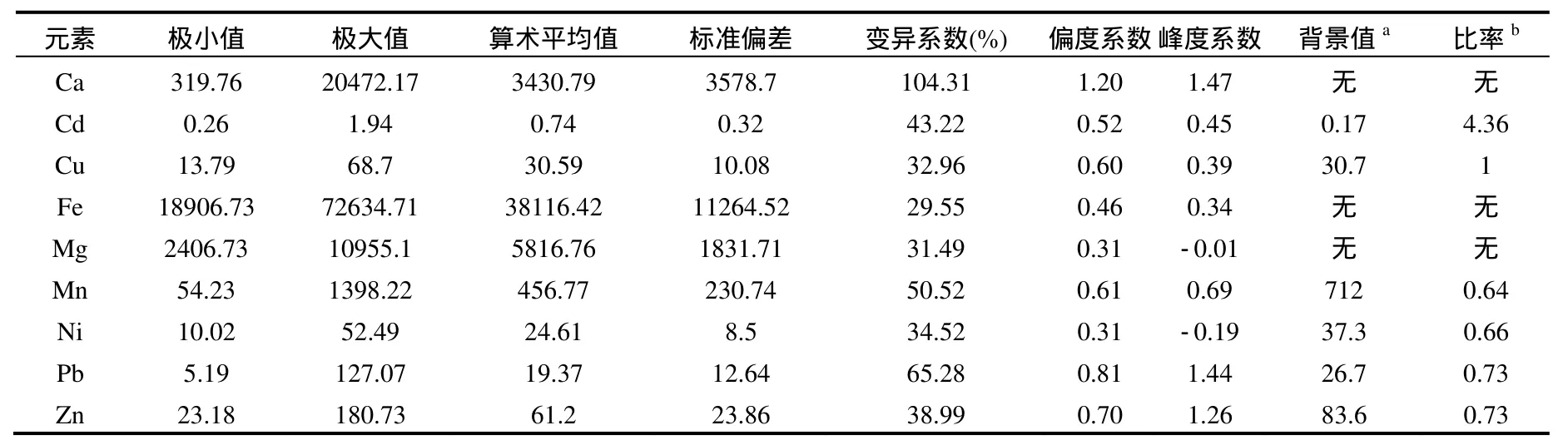
表1 表層土壤重金屬元素濃度(mg/kg)的統計特征值Table 1 Characteristics of statistics of heavy metal concentrations (mg/kg) in topsoils

表2 各主成分對土壤重金屬元素濃度的總體解釋方差百分數Table 2 Total variance explained by different principal components for soil heavy metal concentrations

由表2和表3可見,通過varimax旋轉以后,提取3個因子包含了原來9個指標全部方差的80.53%,說明提取的3個因子能夠比較好地體現原來9種金屬元素的情況.第一主成分與Cd、Cu、Fe、Ni和 Zn相關,占總體方差的 39.6%.第二主成分與Ca、Pb和Zn相關,占總體方差的20.84%.第三主成分與 Mg和 Mn相關,占總體方差的20.08%.圖2所示為根據PCA/APCS源解析計算得到的 Cd污染源的貢獻率.可以看到,在本研究區域內Cd源按照貢獻量依次為源1(占67%)、源 3(占 16%)、其他源(占 9%)和源 2(占 8%).值得注意的是,上述污染源按照貢獻量排列順序與前面按照主成分排列順序(表2)是不同的,如從影響程度上來看,源 2對本研究區域內金屬元素濃度的變化是第二主要因素,但從對 Cd的貢獻量上來看是最小的.雖然本研究是對單一重金屬 Cd源的解析,但是使用多元統計(PCA/APCS受體模型)的方法借助其他重金屬含量的信息較單純的使用重金屬 Cd數據可以得到更多信息,起到更好的解析效果.

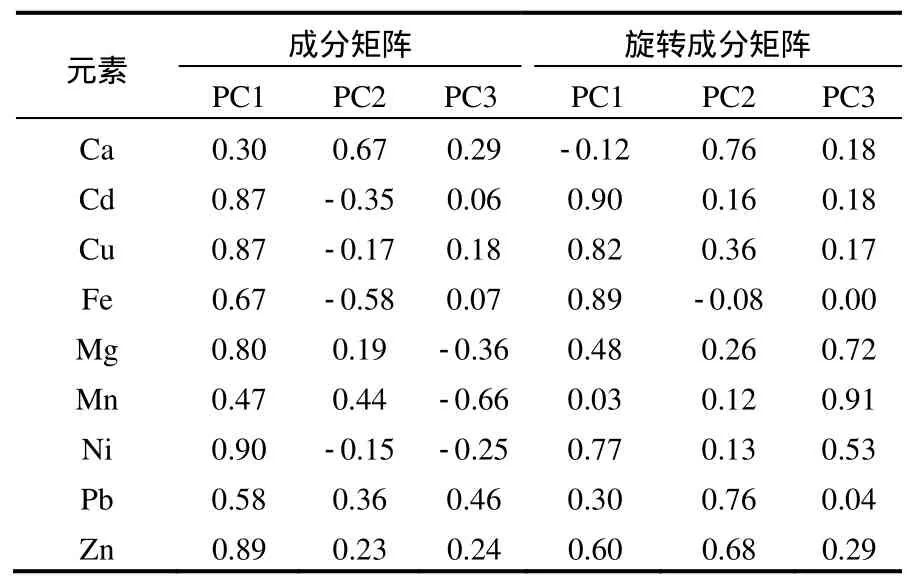
表3 土壤重金屬元素濃度的成分矩陣和旋轉成分矩陣Table 3 The component matrix and rotated component matrix for the concentrations of different soil heavy metals

圖2 Cd源貢獻率Fig.2 Source contribution ratios of soil Cd

2.2 地統計學分析

由于在該研究區域內Cd及Cd源的貢獻量并不是均勻分布的,故在本研究中采用普通克里格來評估Cd及Cd源貢獻量的空間分布特征,如圖3所示.在該研究區域中,源1貢獻了總Cd量的 67%(圖 2),故 Cd的空間分布模式與源 1對Cd貢獻量的空間分布比較相似(圖3).由于第一主成分與Cd、Cu、Fe、Ni和Zn相關(表3),且Cd產生大量富積,故第一主成分所代表的源1可能為人類活動所產生.同時根據源 1對 Cd貢獻量的空間分布圖(圖3b)可知,源1對Cd貢獻量較多的地方主要集中在研究區域的中部,而中部涉及電子方面的工廠較為集中,故推測源 1可能為電子工業源.第二主成分與 Ca、Pb和Zn相關(表3),由于Pb為汽車尾氣排放物,同時結合源 2對 Cd貢獻量的空間分布圖(圖3c)可知,貢獻量由研究區左上方的市中心到郊區呈依次遞減的趨勢變化,而研究區域內西北部靠近市中心的區域又多為建筑用地,故推測源2可能為城市大氣沉降所產生.第三主成分與Mg和 Mn相關(表 3),其中 Mg的變異系數為31.49%(表1),說明Mg的變化比較平均,沒有很大的人為擾動;從圖3d可以看出,第三主成分分布比較分散,在建筑用地區域(北部)、工廠集中區(中部)和待建用地(荒地和農田)區域(東南部)均有較高值出現,同時Mn的平均含量又低于背景值,說明該第三主成分所代表的源 3應主要為成土母質所產生.

3 結論

3.1 研究區域中重金屬元素中 Cd的均值(0.74mg/kg)為其背景值的4.36倍,接近土壤環境質量三級標準(1.00mg/kg)[22],其他重金屬元素均值接近背景值水平,顯示 Cd受到人類活動的強烈影響.由PCA/APCS受體模型可得本研究區域內Cd源貢獻量,按大小依次為源1(占67%)、源3(占 16%)、其他源(占 9%)和源 2(占 8%).同時由地統計學分析和PCA分析,可以進一步推測源1可能為電子工業源,源 2可能為城市大氣沉降源(主要為汽車尾氣),源 3可能為成土母質源.地統計學分析結果顯示,帶來最嚴重污染的Cd源1的貢獻量在空間分布上是不均勻的,在本研究區域的中部的貢獻量最大,而這些正好位于電子工業密集區.

圖3 土壤Cd含量空間分布圖和主要源的貢獻量空間分布Fig.3 The spatial distribution map of soil Cd concentration and the contribution maps of major sources to soil Cd

3.2 本研究采用PCA/APCS受體模型和地統計學相結合的方法,較單一的采用PCA/APCS受體模型提供了更多關于源(主成分)性質方面的信息,能夠更準確的確定源的性質.利用地統計學制圖可以進一步得到源貢獻的空間分布狀況.這些表明,本文提出的PCA/APCS受體模型和地統計學制圖相結合的方法能夠提供較強的源解析能力,是個行之有效的方法.

[1] Simeonov V, Einax J, Tsakovski S, et al. Multivariate statistical assessment of polluted soils [J]. Central European Journal of Chemistry, 2005,3(1):1-9.

[2] Budiansky S. Dispersion modeling [J]. Environmental Science and Technolog, 1980,14(4):370-373.

[3] Henry R C, Lewis C W, Hopke P K. Review of receptor model fundamentals [J]. Atmospheric Environment, 1984,18(8):1507-1515.

[4] 蘇 丹,唐大元,劉蘭嵐,等.水環境污染源解析研究進展 [J]. 生態環境學報, 2009,18:749-755.

[5] 朱 坦,吳 琳,畢曉輝,等.大氣顆粒物源解析受體模型優化技術研究 [J].中國環境科學, 2010,30(7):865-870.

[6] 廖書林,郎印海,王延松,等.遼河口濕地表層土壤中 PAHs的源解析研究 [J]. 中國環境科學, 2011,31(3):490-497.

[7] Ito K, Xue N, Thurston G. Spatial variation of PM2.5 chemical species and source-apportioned mass concentrations in New York City [J]. Atmospheric Environment, 2004,38:5269-5282.

[8] Song Y, Xie S, Zhang Y, et al. Source apportionment of PM2.5 in Beijing using principal component analysis/absolute principal component scores and UNMIX [J]. Science of the Total Environment, 2006,372:278-286.

[9] Mostert M M R, Ayoko G A, Kokot S. Application of chemometrics to analysis of soil pollutants [J]. Trac-Trends in Analytical Chemistry, 2010,29:430-445.

[10] Goovaerts P. Geostatistics for Natural Resources Evaluation [M].New York: Oxford University Press, 1997.

[11] Wang K Y, Shen Y T, Zhang S C, et al. Application of spatial analysis and multivariate analysis techniques in distribution and source study of polycyclic aromatic hydrocarbons in the topsoil of Beijing, China [J]. Environmental Geology, 2009,56:1041-1050.

[12] Davis H T, Aelion C M, McDermott S, et al. Identifying natural and anthropogenic sources of metals in urban and rural soils using GIS-based data, PCA, and spatial interpolation [J]. Environmental Pollution, 2009,157:2378-2385.

[13] Schaefer K, Einax J W, Simeonov V, et al. Geostatistical and multivariate statistical analysis of heavily and manifoldly contaminated soil samples [J]. Analytical and Bioanalytical Chemistry, 2010,396:2675-2683.

[14] GB15618-1995 土壤環境質量標準 [S].

[15] Kaiser H F. The varimax criterion for analytic rotation in factor analysis [J]. Psychometrika, 1958,32:443-482.

[16] Thurston G D, Spengler J D. A qualitative assessment of source contribution to inhalable particulate matter pollution in metropolitan Boston [J]. Atmospheric Environment, 1985,18:1347-1355.

[17] Miller S L, Anderson M J, Daly E P, et al. Source apportionment of exposures to volatile organic compounds. I. Evaluation of receptor models using simulated exposure data [J]. Atmospheric Environment, 2002,36:3629-3641.

[18] Guo H, Wang T, Louie P K K. Source apportionment of ambient non-methane hydrocarbons in Hong Kong: Application of a principal component analysis (PCA)/absolute principal component scores (APCS) receptor model [J]. Environmental Pollution, 2004,129:489-498.

[19] Guo H, Wang T, Simpson I J. Source contributions to ambient VOCs and CO at a rural site in Eastern China [J]. Atmospheric Environment, 2004,38:4551-4560.

[20] Simeonov V, Stratis J A, Samara C, et al. Assessment of the surface water quality in Northern Greece [J]. Water Research,2003,37:4119-4124.

[21] Saito H, McKenna A, Zimmerman D A, et al. Geostatistical interpolation of object counts collected from multiple strip transects: ordinary kriging versus finite domain kriging [J].Stochastic Environmental Research and Risk Assessment, 2005,19:71-85.

[22] 中國環境監測總站.中國土壤元素背景值 [M]. 北京: 中國環境科學出版社, 1990.