基于蒙特卡羅的CTCS-3級列控系統單元重要度分析

車玉龍,蘇宏升

(蘭州交通大學自動化與電氣工程學院,蘭州 730070)

高速列車運行的安全性直接關系到廣大乘客的生命安全，一旦發生事故，后果非常嚴重。為保證行車安全，高速鐵路必須采用列控系統[1]，列控系統的可靠性分析是保障列車安全運行的基礎，因此研究列控系統的可靠性就顯得非常重要。國內一些學者對CTCS-3級列控系統的可靠性[2-3]與安全性[4]進行了分析與評估研究。但是目前對組成CTCS-3級列控系統組成單元的重要度研究較少，而單元的重要度是系統可靠性分析的重要內容。

故障樹分析(Fault Tree Analysis，FTA)是用于大型復雜系統可靠性和安全性分析的一個有力工具，FTA反映了單元失效、人為失誤或子系統等事件引起頂事件發生的邏輯關系。近年來使用FTA方法研究鐵路系統[5]及高速鐵路列控系統的安全風險[6]取得了較好的效果。若故障樹太復雜，尤其底事件不服從指數分布時，則會遇到計算量相當大的問題。蒙特卡羅方法簡單、高效，其基本思想是通過計算樣本均值來估計總體均值，用蒙特卡羅仿真求解故障樹，對底事件所服從的分布類型沒有限制，在很多領域得到了廣泛應用[7-9]。

由實際經驗知，系統中的單元并非同等重要的，如有的單元一旦失效就會引起系統失效，有的則不然。本文在深入分析CTCS-3級列控系統結構和功能的基礎上，從系統失效的角度建立CTCS-3級列控系統失效的故障樹模型，采用蒙特卡羅方法仿真故障樹，計算CTCS-3級列控系統組成單元的概率重要度和結構重要度，從而識別列控系統的薄弱環節，為提高列控系統的可靠性和日常維護提供科學依據。

1 故障樹分析方法

FTA是1961年由美國貝爾實驗室的H.A.Wastson和D.F.Haasl首先提出的，采用邏輯框圖(即故障樹)形象地對可能造成系統的故障因素(包括硬件、軟件、環境和人為因素等)進行分析，特點是思路清晰，邏輯性強，直觀明了，既能定性分析，又能定量分析。通常進行FTA的程序是：選擇頂事件，建立故障樹，以及定性或定量地評定故障樹。

在一個故障樹中往往包含有很多的基本事件，這些事件并非是同等重要的，一般認為，一個基本事件或最小割集對頂事件發生的貢獻稱為重要度。一個單元重要度的衡定與該單元在系統整個生命周期不同階段有不同的意義，在系統設計階段，單元重要度的衡量可以用來識別薄弱點，用來提高整個系統的可靠性；在系統工作階段，單元重要度的衡量可以用來合理分配維修和檢查資源以保證更重要的單元。工程上常用的有概率重要度和結構重要度。

1.1 結構重要度

結構重要度是基本事件在故障樹所在的位置對故障樹整體的影響程度。即在假定各基本事件的發生概率都相等，或者說不考慮基本事件自身的發生概率的前提下，分析各基本事件的發生對頂事件發生所產生的影響。

設j是系統中任一單元，系統的結構函數為φ，若φ(0j,x)=0,φ(1j,x)=1，則表示j是一個關鍵部件，表明j正常時系統就正常，j失效時系統也失效。稱(1j,x)為j的一個關鍵路向量。對于j單元某一給定狀態，其余(n-1)個單元的可能狀態組合共有2n-1種不同的結果，定義

nφ(j)=∑{φ(1j,x)-φ(0j,x)}

nφ(j)是第j個單元對系統失效貢獻大小的量度。定義單元的結構重要度為

Iφ(j)=12n-1nφ(j)

它表明j的關鍵路向量數目在所有2n-1中可能情形中占的比例。因此，對任意的結構φ，單元可按其結構重要度排序。

1.2 概率重要度

結構重要度僅僅反映的是基本事件在故障樹中所占位置的重要程度，而設備在系統中的重要性不僅依賴于其結構，還依賴于設備本身發生故障的概率。設備的概率重要度是指某設備故障發生概率的單位變化量所引起的系統故障發生概率的變化值，也即設備故障發生概率對該系統故障發生概率的變化率，稱

Ih(j)=?h(p)?pj,j=1,…,n

為設備j的概率重要度。

2 蒙特卡羅方法

蒙特卡羅方法的基本思想是通過計算樣本均值來估計總體均值，其理論基礎是概率統計，基本手段是隨機抽樣，通過有關隨機變量的統計抽樣檢驗或隨機模擬，從而估計和描述函數的統計量、求解問題近似解的一種數值計算方法，處理實際問題的基本步驟是：建立隨機模型，定義隨機變量，過程模擬，統計計算。

2.1 隨機數

從蒙特卡羅方法的基本思想可以看出，對給定的分布進行抽樣，得到一個隨機數樣本的過程在蒙特卡羅方法中占有非常重要的地位。隨機數的產生可以分為均勻分布隨機數的產生和非均勻隨機數的產生2個方面，每一方面又有多種產生方法。

通過反函數法產生任意分布隨機數是最常用的方法之一。將累積分布函數F(x)進行反變換，得到所需的反函數G(F(x))，通過G(F(x))就得到F(x)的隨機數。顯然累積分布函數F(x)取值范圍為0～1，因為F(x)的定義為F(x)=P(X≤x)，為了生成一個概率分布的隨機抽樣，將生成一個在0～1之間的隨機數(r)。然后將這個值帶入到G(r)=x中得到符合分布F(x)的隨機數。

2.2 基于蒙特卡羅的故障樹模擬過程

用蒙特卡羅方法對故障樹進行仿真具體有2種方法：基于最小割集的故障樹仿真和基于結構函數的故障樹仿真。基于最小割集的故障樹仿真是對故障樹的所有最小割集進行故障時間抽樣，把這些最小割集故障時間的最小值作為系統失效故障時間的一個抽樣值，記錄此故障時間。重復此過程，最后通過對記錄樣本的統計分析，得到各個可靠性結果。后者是根據故障樹的結構函數，通過抽樣故障樹的基本元件，對其失效時間進行排序，再依次檢查各個底事件失效是否會引起頂事件發生，從而找出頂事件發生時間[8]。本文使用基于最小割集的故障樹仿真，因為這種仿真方法能夠準確定位系統中某單元的失效是否導致系統失效，且仿真過程中不用通掃整個故障樹，也不用求取系統故障樹的結構函數，相比之下仿真流程較簡單，可以節省仿真時間。

2.3 計算重要度

(1)單元的結構重要度

Iφ(j)=P(j)N

其中，P(j)表示基本單元失效引起系統失效的次數；N表示基本單元失效總次數。

結構重要度表示了設備失效而引起系統失效次數在系統總失效中的百分比，因此Iφ(j)越大，說明越是系統可靠性薄弱環節。

(2)單元的概率重要度

Ih(j)=H(j)N

其中，H(j)表示基本單元失效引起系統失效的次數；N表示基本單元失效總次數。

概率重要度表示單元在系統中的重要程度，若Ih(j)=1，則說明只要設備j發生一次故障，則系統必定因其發生失效，為了提高系統可靠度，首先應該著眼于概率重要度較大的設備。

3 算例

3.1 CTCS-3級列控系統介紹

CTCS-3級列控系統是基于GSM-R無線通信實現車、地信息雙向傳輸，無線閉塞中心(RBC)生成行車許可，軌道電路實現動車組占用檢查，應答器實現列車定位，滿足動車組運營速度350 km/h和最小追蹤間隔3 min的要求，同時具備CTCS-2級列控系統功能的列車運行控制系統[10]。

CTCS-3級列控系統的結構如圖1所示，包括地面子系統和車載子系統，車載子系統包括安全計算機(VC)、軌道電路信息接收單元(TCR)、應答器傳輸模塊(BTM)及應答器天線、無線傳輸模塊(RTM)、人機界面(DMI)、動車組接口單元(TIU)、測速測距單元(SDU)、司法記錄器(JRU)等單元，地面子系統由無線閉塞中心(RBC)、列控中心(TCC)、軌道電路、應答器系統(含軌旁電子單元LEU)和臨時限速服務器(TSR)構成。

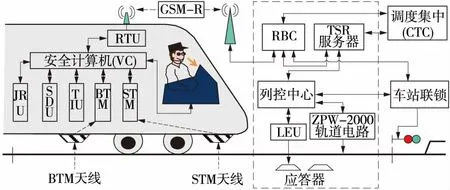
圖1 CTCS-3級列控系統結構示意

3.2 故障樹建立

CTCS-3級列控系統屬于可維修系統，在分析之前先做以下假設：(1)各單元的壽命分布均服從指數分布；(2)每次故障的事件是獨立事件，與其他事件無關；(3)不考慮共因失效；(4)系統中涉及到的比較器、表決器和司法記錄器(JRU)等是完全可靠的，即故障率λ為0。

本文從CTCS-3級列控系統安全功能失效的角度出發，建立CTCS-3級列控系統的功能結構故障樹，按照建立故障樹的基本步驟，首先選擇CTCS-3級列控系統失效為頂事件，根據各事件的功能邏輯關系由上到下建立故障樹，如圖2所示。

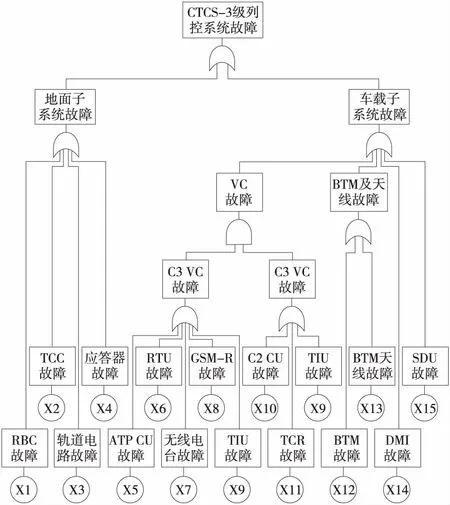
圖2 CTCS-3級列控系統失效的FTA圖

3.3 仿真結果

車載子系統的故障率數據來源于文獻[2]，列控中心、軌道電路和應答器的故障率參數來源于文獻[11]，RBC的故障率來源于ETCS(歐洲列車運行控制系統)中RBC的參數[12]。

蒙特卡羅仿真參數設置：有效失效時間下限為0，有效時間上限為1 000，隨機數種子為100，分別模擬2 000次，4 000次，8 000次和10 000次。CTCS-3級系統設備(底事件)的結構重要度和概率重要度仿真計算結果如表1所示。

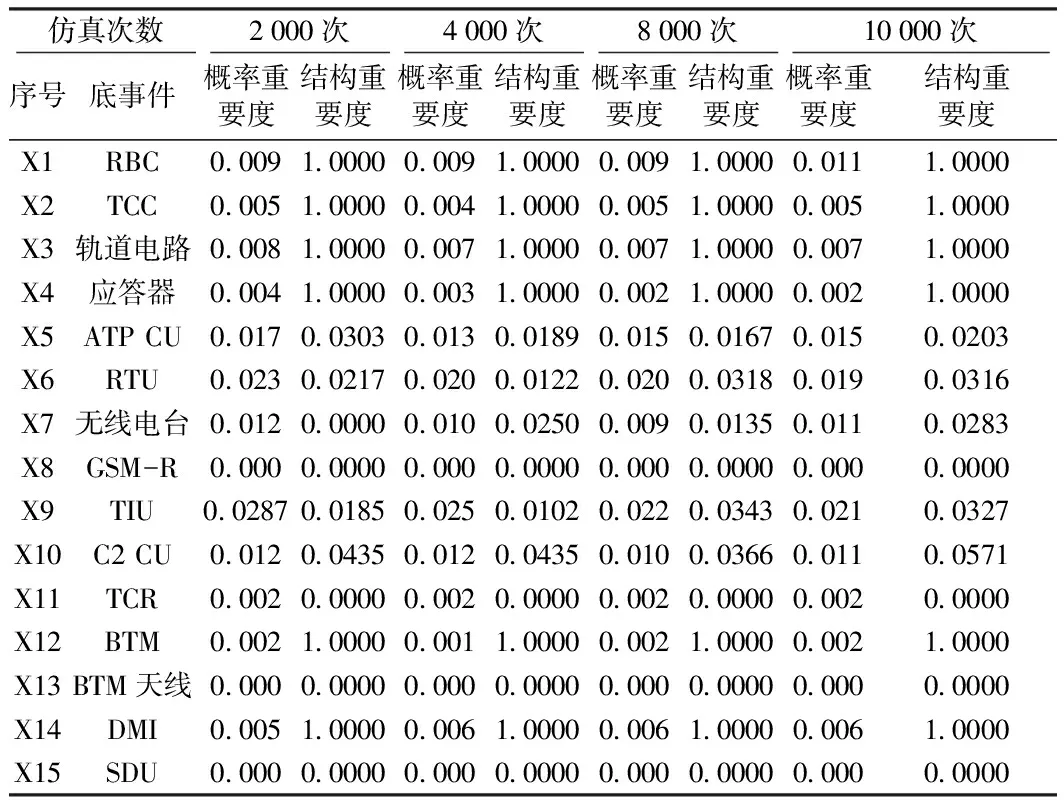
表1 CTCS-3級列控系統設備的重要度

從表1中可以看出，隨著仿真次數的增大，仿真結果趨于穩定。從仿真10000次的結果可以看出，概率重要度排序是：TIU>RTU>ATP CU>RBC=C2 CU=無線電臺>軌道電路>DMI> TCC>BTM=TCR=應答器>SDU=BTM天線=GSM-R；結構重要度排序是：RBC=TCC=軌道電路=DMI=BTM=應答器> C2 CU> TIU > RTU >無線電臺> ATP CU>TCR=SDU=BTM天線=GSM-R。

為了提高列控系統的可靠性，應該著眼于概率重要度較大的設備，例如列車接口模塊(TIU)的概率重要度大于GSM-R。從結構重要度的排序結果可以看出，列控系統地面設備較車載設備而言，列控中心(TCC)、軌道電路、應答器、人機界面(DMI)和應答器信息接受模塊(BTM)等是列控系統可靠性的薄弱環節。

4 結語

在深入分析CTCS-3級列控系統結構和功能的基礎上，從系統失效的角度建立CTCS-3級列控系統失效的故障樹，采用蒙特卡羅方法對故障樹進行仿真計算，得到列控系統組成單元的概率重要度和結構重要度，為提高列控系統設備的日常維護和管理者的科學決策提供依據。

[1] 張曙光.CTCS-3列控系統總體技術方案[M].北京：中國鐵道出版社，2008．

[2] 邸麗清，袁湘鄂，王永年.CTCS-3級列控系統RAM指標評價方法研究[J].中國鐵道科學，2010，31(6):92-97．

[3] 吳書學.CTCS3-300T列控車載系統運行可靠性分析[J]. 鐵路通信信號工程技術，2012，9(1):8-11．

[4] 石先明，張敏慧.高速鐵路列控系統安全性分析與改進[J].鐵道標準設計，2012(11):101-106．

[5] 劉敬輝，戴賢春，郭湛，等.鐵路系統基于風險的定量安全評估方法[J].中國鐵道科學，2009，30(5):123-128．

[6] 張苑，劉朝英，李啟翮，等.無線閉塞中心系統安全風險分析及對策[J].中國鐵道科學,2010，31(4):112-117.

[7] 庫明陽，郭建英.基于故障樹的系統可靠性仿真分析[J].計算機仿真，2007，24(8):78-80．

[8] 馬小玲.基于蒙特卡羅的故障樹模型的仿真研究[J].電子設計工程，2011，19(3):128-130．

[9] 康健，周振華.基于費用最小的列控設備維修優化與仿真[J].鐵道標準設計，2012(12):92-95．

[10] 鐵道部.科技運[2008] 127號 CTCS-3級列控系統需求規范(SRS) (V1.0) [S].北京：中國鐵道出版社，2008.

[11] 李清.CTCS-2級列控系統安全可靠性分析及運用研究[D].成都:西南交通大學，2010．

[12] UNISIG SUBSET 088， ETCS Application Levels 1 & 2 — Safety Analysis， Version 2.3.0， http://www.era.europa.eu/Document-Register/Pages/UNISIGSUBSET-088.aspx.