復合材料多向層壓板疲勞壽命預測①

景 釗，孫 秦

(西北工業大學航空學院，西安 710072)

0 引言

纖維增強樹脂基復合材料層壓板在航空航天飛行器結構中的應用越來越廣泛。層壓結構在工作中經常受到交變載荷作用，在交變載荷作用下，結構的疲勞損傷問題就突顯出來。復合材料的脆性、損傷演變的復雜性、不同鋪層間的耦合效應以及層間應力的作用，使得復合材料的疲勞問題變得復雜。因此，對復合材料疲勞的研究工作十分重要。

常用的復合材料疲勞損傷理論［1－6］有剩余強度模型、剩余剛度模型、疲勞模量模型、連續介質結合離散模型等。這些方法較突出的問題主要是在疲勞損傷參量定義、損傷演化規律構造和結構件疲勞壽命預測系統框架的合理構筑上，對不同載荷形式和鋪層方式層壓板的疲勞壽命預測，現有理論并不能給出一個較為普適的工程計算方法。

本文基于單向板疲勞模型理論，對3個炭纖維/樹脂基T300/QY8911單向層壓板的疲勞壽命進行了預測，給出了擬合表達式，在考慮多向層壓板層間應力及耦合作用的情況下，給出了一套完整的疲勞壽命預測方法。同時，為了驗證本文提出的疲勞壽命預測方法，對不同鋪層方式的2種多向層壓板在2種載荷工況下進行了疲勞試驗，并對其疲勞壽命進行了預測。

1 單向層壓板疲勞壽命模型

1．1 單向層壓板壽命估算模型

根據Wang和Han提出的復合材料層壓板的疲勞模量理論［5－9］，在等幅循環載荷作用下，把 q-lgN曲線(載荷幅值比q=σmax/σut，表征載荷的應力水平)區分為凸型和直線型，凸型形式為

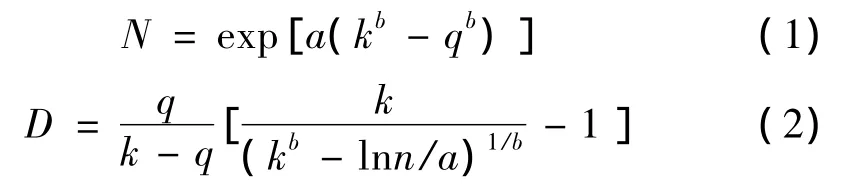
其中，a、b、k均通過試驗的q-lgN曲線擬合求出，σmax和σut分別為加載方向上試件的循環最大應力和靜態極限應力;D為累積應變損傷，它是循環次數n以及疲勞壽命N的函數，滿足邊界條件:D(0，N)=1，D(N，N)=1。若取損傷函數:D(n，N)=n/N，則這種損傷累積的概念簡化成Miner線性累積損傷理論。當b=1．0時，方程(1)、(2)退化為直線型。

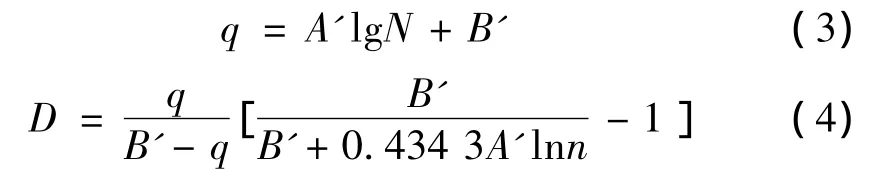
1．2 單向板在多軸循環應力作用下的疲勞損傷［10］

單向層壓板在多軸循環應力作用下，當疲勞損傷累積達到一定數值后，將發生纖維失效，或基體開裂，從而導致層壓板的破壞。設單向板同時有σ1、σ2和σ6主軸循環應力作用，引入等效幅值比ˉq1、ˉq2和ˉq6:

式中 v21=E2·v12/E1，對應相應的加載載荷;Xut、Xuc分別為拉伸、壓縮極限強度。

相應的累積損傷計算模型為

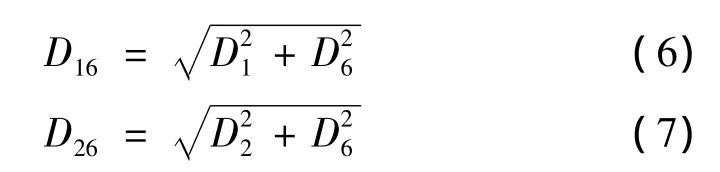
式中 D1，D2和D6分別為單向板沿纖維方向(縱向)、橫向和剪切時累積損傷，由等效ˉq值代入單軸應力時的損傷表達式(2)、(4)求出。

只要D16或D26中任一個首先達到1．0時，單向板就失效。當D16＞D26時，纖維失效;反之，則為基體拉壓或剪切失效。

2 多向層壓板疲勞壽命模型

多向層壓板疲勞壽命的預測需模擬復合材料損傷累積和疲勞失效的完整過程，同時計算層壓板的累積損傷和最終的疲勞壽命。多向層壓板在疲勞載荷作用下，失效層的破壞原因有2種:(1)由于損傷累積發生局部疲勞破壞;(2)因為靜強度不足導致局部靜力破壞。這取決于外載荷是大于最先失效強度還是小于最先失效強度，應力分布每改變一次，都要計算層壓板的最先失效強度，并和外載荷進行比較，確定可能發生破壞的單向層，并判斷其破壞原因。

在循環應力作用下，多向層壓板的總體破壞是因為每個單層逐次發生了疲勞破壞或靜力破壞，其壽命用先后發生疲勞破壞的單層壽命的累積和表達。疲勞壽命分析的步驟:(1)在應力分析的基礎上，判斷最先失效的單層是發生局部疲勞破壞還是發生靜力破壞;(2)對于發生疲勞破壞的單層，計算循環應力引起的累積損傷和疲勞壽命，對于發生靜力破壞的單層，計算和靜力破壞等效的疲勞累積損傷與壽命;(3)選擇合適的剛度衰減準則對發生疲勞破壞或靜力破壞的單層進行剛度退化;(4)返回第1步重復上述過程，直到隨著單層逐次失效，最終導致層壓板總體失效，用失效單層的疲勞壽命累積和表示層壓板的疲勞壽命，其分析過程見圖 1［11］。

圖1 多向層壓板的疲勞分析模型Fig．1 Analysis model of the multidirectional laminate fatigue life

2．1 多向層壓板的剛度分配及層合效應

多向復合材料層壓板的單軸疲勞壽命估算是在單向層壓板單軸疲勞損傷估算模型基礎上，通過逐一單向層板的疲勞破壞線性累加而建立的。根據剛度分配原則，計算出多向層壓板中各角鋪層板的單軸分配載荷。由于層壓效應對層合板強度的增強作用，本文給出一個靜強度增強效應系數，進而計算各角鋪層板的疲勞壽命。對于多向層壓板，各角鋪層板的單軸載荷按載荷方向剛度分配。

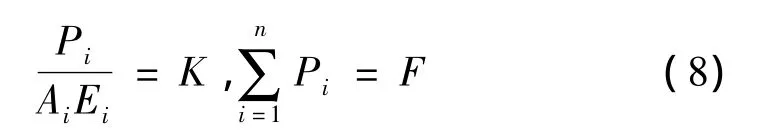
式中 n為不同鋪設方向角的總數;F為層壓板施加的軸向總載荷;Pi為各角鋪層的軸向分配載荷;Ai為第i種角鋪層截面積;Ei為第i種角鋪層的加載方向剛度。

由式(8)得到各角鋪層板的加載軸向載荷為

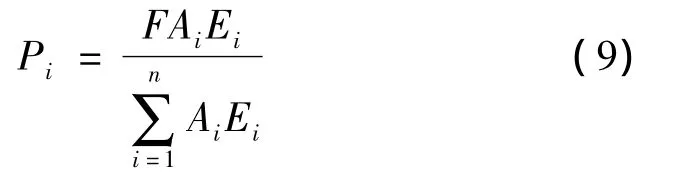
各角鋪層加載方向下的偏軸剛度可由材料主軸彈性常數 E1、E2、G12及泊松比 v12得到。

根據不同類型的多向層壓板靜強度試驗后的數據，由剛度分配折算出各單向層的靜強度，用σs表示;取單向板靜力試驗的相應靜強度數值用σu表示，兩值相比:

γ為多向板的靜強度增強效應系數。將增強效應系數作用于各單向板所承載的應力水平，取σmax/γ作為各單向板的疲勞壽命估算的應力水平，此靜強度增強效應系數可合理反映層合效應導致的剛度增強作用。

2．2 多向層壓板疲勞失效準則

當外加載荷大于某個單層最先失效強度，某個單層的纖維被立即拉斷，或基體立即開裂。此時，其他單向層并沒有完全破壞，需對其進行相應的剛度退化，同時應力重新分布。

本文采用的剛度衰減原則:(1)縱向纖維失效時，單向層剛度全退化為零;(2)橫向纖維失效時，Q12=Q22=0，其余保留;(3)剪切失效時，Q12=Q22=Q66=0，Q11保留。單向層面內靜強度破壞準則應用平面應力狀態下的Tsai-Hill強度準則判定:

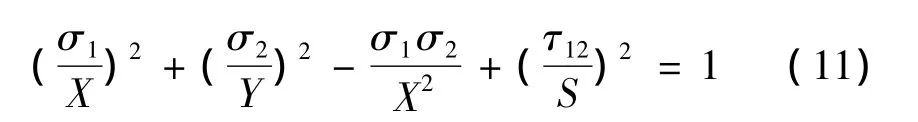
對于拉伸應力，X、Y用拉伸強度;對于壓應力，X、Y用壓縮強度。

2．3 多向層壓板層間應力計算

纖維增強復合材料層壓板自由邊層間應力奇性及其引起的分層損傷，將導致復合材料層壓板分層與擴展，從而引起層壓板的分層疲勞破壞。本文給出一種基于力平衡關系的多向板層間應力的簡化算法［12］:自由邊區域層間應力分布在1～2個板厚區域內，且這一區域大部分范圍內數值很小，到十分靠近自由邊時，才急劇上升。因此，假設τyz與τxz的分布如圖2(a)所示，σz分布如圖2(b)所示。

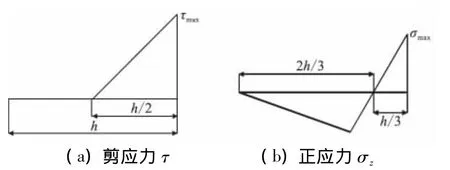
圖2 剪應力和正應力分布假設Fig．2 The assumption of shear stress and normal stress

由圖(2)根據力的平衡關系，可得到兩不同鋪向角層組間的層間奇性應力值由式(12)計算:

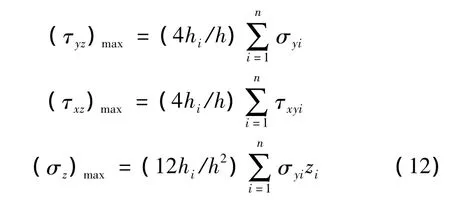
式中 hi為2不同鋪向角層組間厚度較大者;h為2不同鋪向角層組的總厚度;zi為第i層中面到被求層間的距離。

由式(12)獲得的層間應力可能發生層間靜力或疲勞破壞，層間靜力破壞判據［13］為

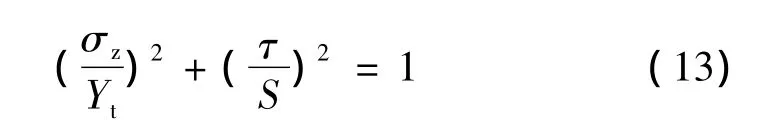
當式(13)大于1時，認為層間發生靜力破壞，多向層壓板的疲勞壽命則按分層后各層組的疲勞壽命累加。當式(13)小于1時，認為多向層壓板疲勞過程中將發生層內疲勞破壞，且存在多向板的疲勞壽命增強效應。

2．4 多向層壓板疲勞壽命估算方案

在循環載荷加載過程中，層壓板因為各單層先后發生疲勞破壞或靜力破壞而失效，每個發生疲勞破壞的單層存在一個疲勞壽命，用這些壽命的累積和表達層壓板的疲勞壽命。本文給出了一個考慮分層效應與靜強度增強效應耦合的壽命估算方案。整個多向層板疲勞壽命估算方案如圖3所示。

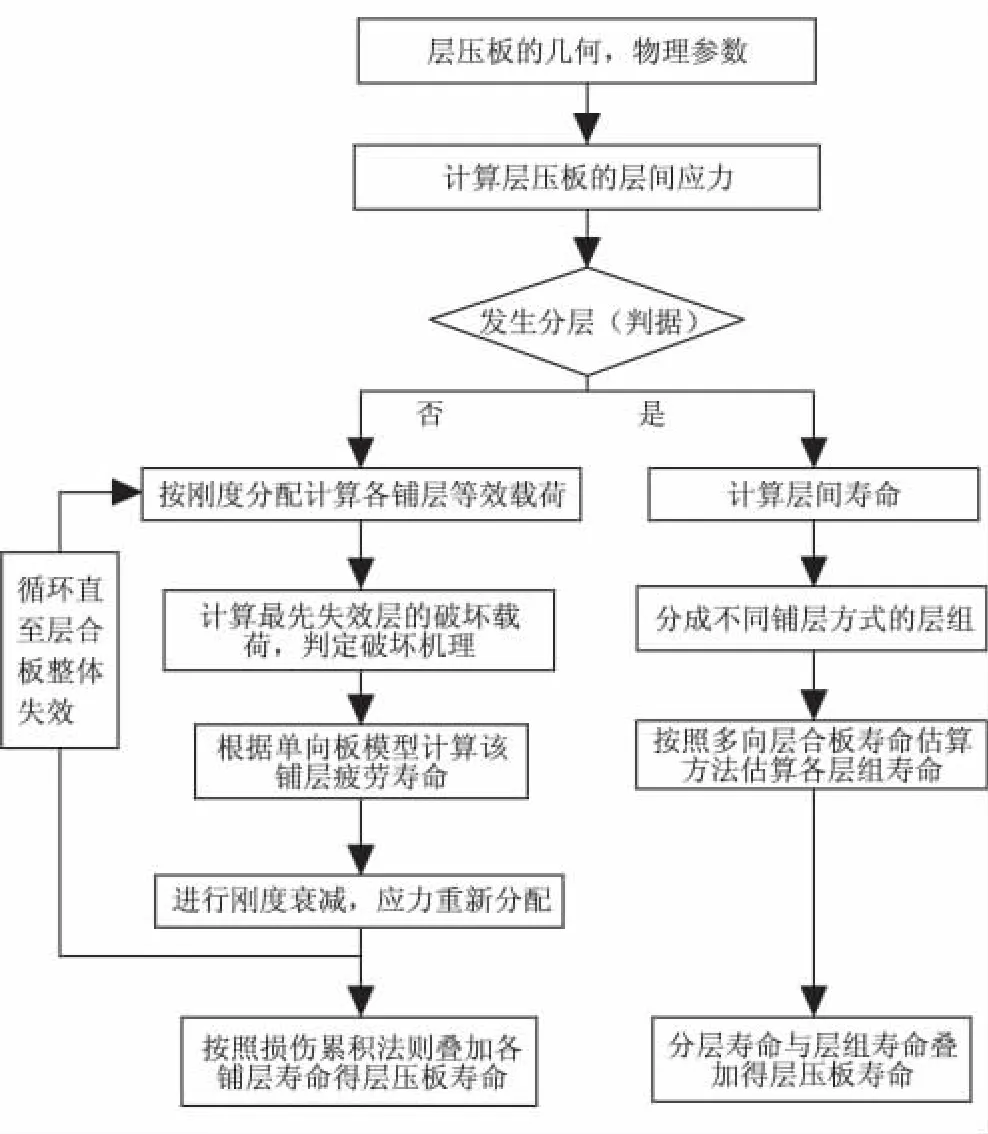
圖3 層壓板疲勞壽命預測框圖Fig．3 Block diagram of the fatigue life prediction model for CFRP composite laminate

首先，計算層壓板層間應力，判定是否發生層間破壞。如果不發生層間破壞，多向層壓板的壽命估算需算出最先失效的單向層疲勞破壞壽命，按耦合效應失效模式確定剛度退化，再重新計算其他未疲勞破壞的單向層應力狀態，繼續計算后續最先失效狀態單向層的疲勞破壞壽命。如此反復，直至多向層板因為各單向層的失效而最終整體失效。根據疲勞損傷的累積法則［14］，上述多向層壓板的疲勞損傷累積過程可用估算方程描述為

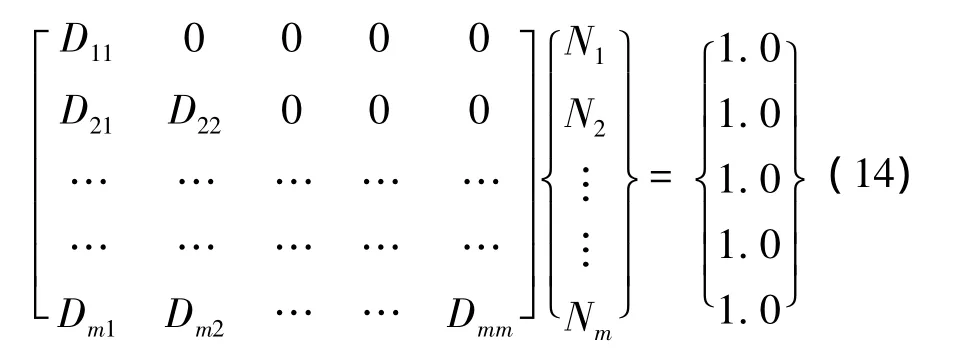
式中 Dij為層壓板各角鋪層的等效疲勞損傷，其中行號i從1到m代表層壓板內不同角鋪層單向層破壞的先后順序;列號j從1到m表示在一個循環載荷水平內隨著加載次數增大對不同角鋪層單向層造成的疲勞損傷;Ni則為不同鋪層角單向層的疲勞壽命。

由矩陣可看出，每一個單向層的疲勞損傷按載荷循環重分配是累加的，即每一行內部元素疊加，得到該角鋪層的疲勞損傷;對角線元素疊加，即得到整個層壓板在一個循環載荷內的疲勞損傷。因此，得多向層壓板總的疲勞壽命為

如果判定發生層間破壞，層壓板發生分層損傷進而分層。需要計算層間壽命與分層后各個層組的壽命，這里僅考慮發生一次分層的情況。層間破壞認為是膠體破壞，所以層間壽命按照單向剪切板的壽命估算公式進行估算;分層后各個層組的壽命按式(16)［12］計算:

3 實驗驗證

3．1 單向板疲勞模型與實驗驗證

首先，基于單向層壓板的疲勞模量模型，對炭纖維/樹脂基T300/QY8911單向層壓板壽命進行了預測，復合材料單向層壓板在多級應力水平下進行疲勞試驗，每個應力水平下都有5個試驗件。試驗件構型即實驗類別:［0］20縱向拉-拉疲勞試驗，［90］20橫向拉-拉疲勞試驗，［0/90］10面內剪切疲勞試驗。試驗件的單向鋪層厚度為0．155 mm，總厚度為3．1 mm。用最小二乘法所獲得的材料擬合常數見表1。

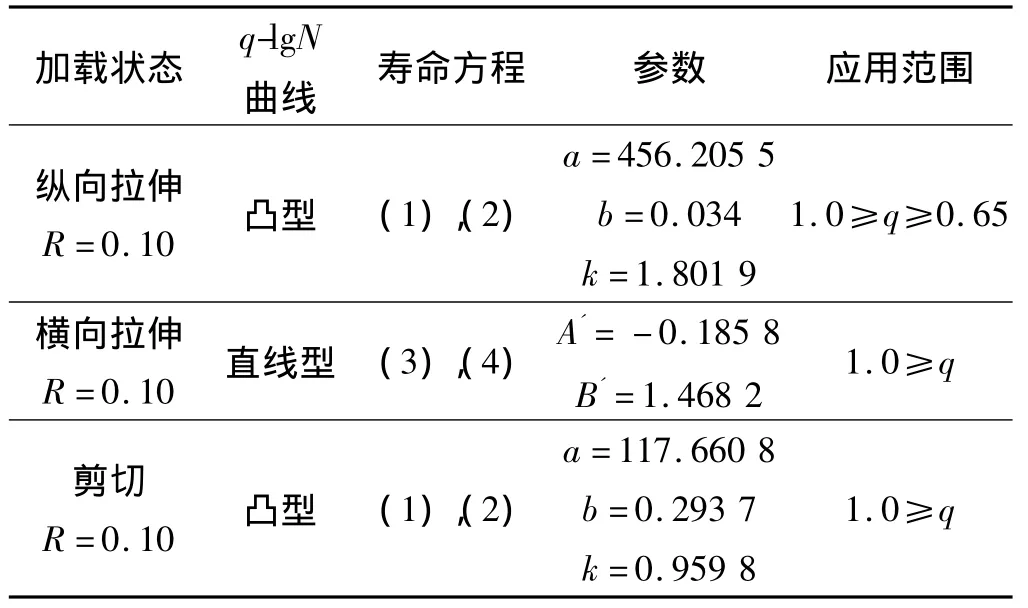
表1 單向板疲勞試驗數據擬合參數(q=σmax/σult)Table 1 Fitting parameters of the unidirectional laminate with fatigue experimental data(q=σmax/σult)

3．2 多向板疲勞模型與實驗驗證

靜力拉伸及面內剪切實驗試件均夾持于MTS-810試驗機的夾頭中，都以2 mm/min的加載速度連續加載，直到試件破壞，連續記錄載荷-應變和載荷-橫梁位移數據，試件的破壞載荷及形態。靜力拉伸試驗與面內剪切類試驗層壓板試驗件疲勞破壞圖片如圖4所示。

圖4 靜力拉伸和面內剪切試驗件疲勞破壞Fig．4 Fatigue failure under cyclic tension load and cyclic shearing load

對2種多向層壓板分別進行了縱向拉-拉和面內剪切實驗，兩種層壓板的鋪層即厚度分別為［45/0/0/0/－45/90/45/0/0/－45］S單層厚 1．55 mm，總厚度3．1 mm;［45/－45/－45/45］S單層厚0．217 mm，總厚度1．736 mm。材料主軸下的彈性模量如表2所示。

表2 單向層壓板彈性模量Table 2 Elastic modulus of unidirectional laminate

根據層壓效應具有增強作用，采用增強效應系數計算方法，獲得的最終結果見表3。

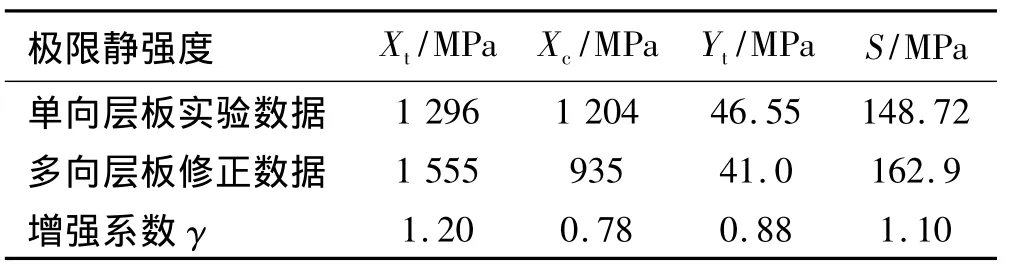
表3 單向層壓板靜強度修正值Table 3 Static strengths of unidirectional laminate

通過表3可看到，多向層壓板由于耦合效應在縱向拉伸與剪切作用下，其強度是有所增強的，而在縱向壓縮以及橫向拉伸情況下，強度有所削減。

為了驗證提出的預測方案，對于在不同加載方式下兩種鋪層方式的層壓板的疲勞壽命，均按照圖3的估算流程進行預測。對于鋪層分別為［45/0/0/0/－45/90/45/0/0/－45］S，［45/－45/－45/45］S的層壓板，測得靜力拉伸破壞強度分別為 1 025．5、239．7 MPa，疲勞壽命估算及其與試驗均值比較見表4、表5;面內剪切的破壞強度分別為 262．6、189．8 MPa，疲勞壽命估算及其與試驗均值比較見表6、表7。表中Nexp為5個試件在該應力水平下測得的有效壽命均值，Npre為模型估算壽命。

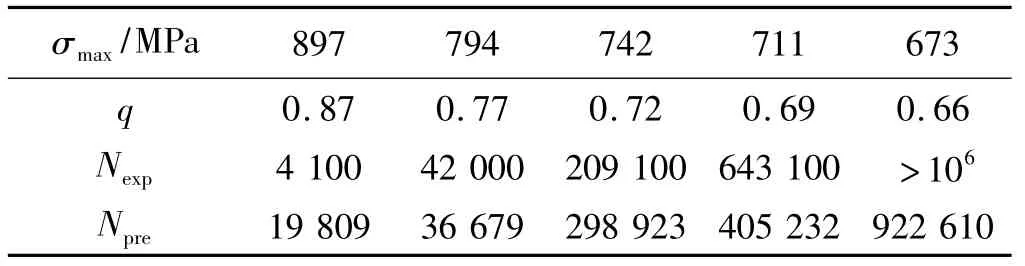
表4 層壓板［45/0/0/0/－45/90/45/0/0/－45］S縱向拉伸(R=0．1)壽命估算Table 4 Life prediction of the laminate［45/0/0/0/－45/90/45/0/0/－45］S under longitudinal tension load(R=0．1)

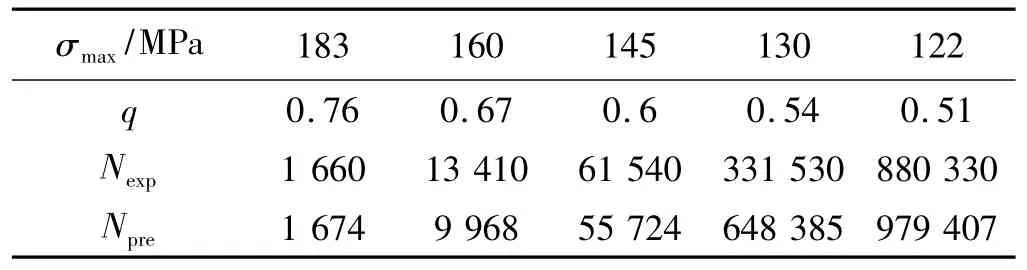
表5 層壓板［45/－45/－45/45］S縱向拉伸(R=0．1)壽命估算Table 5 Life prediction of the laminate［45/－45/－45/45］S under longitudinal tension load(R=0．1)

通過以上模型預測數據與實驗數據的表格對比可看出，模型有較強的預測能力，尤其是在q≤0．85這個范圍內時，模型的預測誤差較小，適宜在工程計算中運用。當0．85＜q＜1時，由于疲勞破壞快速發生，破壞機理復雜，且實驗數據分散性較大，這是導致q在此范圍內存預測壽命與實驗均值有較大誤差的原因。

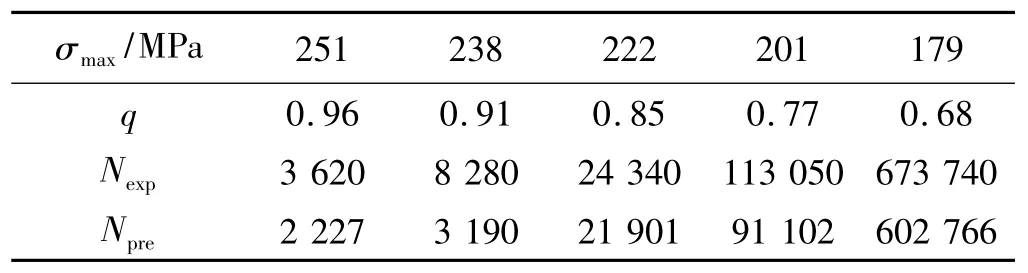
表6 層壓板［45/0/0/0/－45/90/45/0/0/－45］S面內剪切(R=0．1)壽命估算Table 6 Life prediction of the laminate［45/0/0/0/－45/90/45/0/0/－45］S under shearing load(R=0．1)

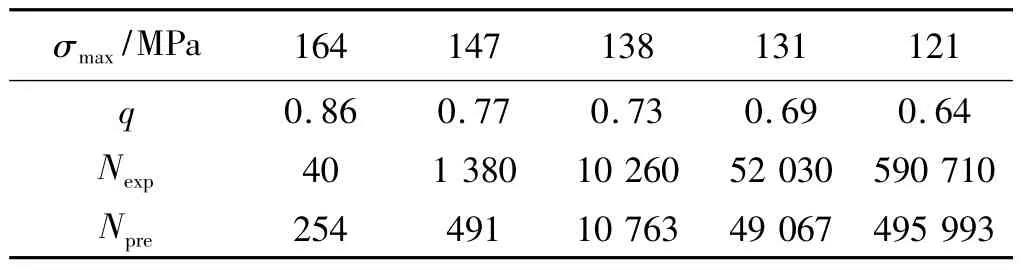
表7 層壓板［45/－45/－45/45］S面內剪切(R=0．1)壽命估算Table 7 Life prediction of the laminate［45/－45/－45/45］S under shearing load(R=0．1)

4 結論

(1)提出了一種考慮層壓板耦合效應的多向層壓板疲勞壽命預測方法，該方法考慮了層間效應對疲勞強度的增強作用，以及層間邊緣奇性導致的疲勞強度的降低。通過實驗驗證了模型能夠很好地預測多向板層壓板的疲勞壽命，適宜在工程計算中運用。

(2)層間效應對層壓板的疲勞強度并不都是增強的作用，對于不同的載荷形式有所不同，僅在靜力拉伸與面內剪切載荷下，疲勞強度有所增強，本文通過實驗驗證得出了此結論。

(3)本文的預測方法同時考慮了主受力件宏觀唯象的結構變化與次受力件中由于損傷形成的各單層應力重分配的細微力學表現，且不依賴于試件鋪疊方式和受載形式，建立的理論分析流程和預測方法適宜在各種工況下運用，有較廣的應用前景。

［1］ 張志民，張開達，楊乃賓．復合材料結構力學［M］．北京航空航天大學出版社，1993．

［2］ Yao W X，Himmel N．A new cumulative fatigue damage model for fiber reinforced plastics［J］．Composites Science and Technology，2000，60(1):59-64．

［3］ 顧怡．FRP疲勞累積損傷理論研究進展［J］．力學進展，2001，31(2):193-202．

［4］ Han K S，Hwang W．Fatigue life prediction and failure mechanisms of composite materials［J］．Advanced Composite Materials，1992，3(1):29-52．

［5］ 韓京變，黃云峰，張金明．復合材料疲勞壽命預測［J］．復合材料學報，1987，3(4):16-24．

［6］ Han K S，Hwang W．Fatigue of composites-fatigue modulus concept and life prediction［J］．Composite Materials，1986，2(4):154-165

［7］ 顧怡，姚衛星．疲勞加載下纖維復合材料的剩余強度［J］．復合材料學報，1999，8(3):98-102．

［8］ 王丹勇，溫衛東．復合材料單向層合板損傷失效研究［J］．復合材料學報，2007，10(5):142-148．

［9］ 張開達，李亞智．計及平均應力影響的疲勞壽命估算方法［C］//復合材料的現狀與發展．毛天祥．NCCM211 11屆全國復合材料學術會議論文集，合肥，ISBN 7231220119825PTB．4，中國科技大學出版社，2000，10:613-617．

［10］ 李亞智，張開達，張博平．一種FRP累積損傷模型及其在結構疲勞壽命估算中的應用［J］．應用力學學報，2003，3(1):54-58．

［11］ 董興建．復合材料層壓結構疲勞壽命預測方法研究［D］．西北工業大學，2002．

［12］ 諸強，楊智春，張開達．一種計及分層效應的復合材料層合板疲勞壽命計算方法［J］．西北工業大學學報，2005，12(6):708-712．

［13］ Hashin Z，Rotem A．A fatigue failue criterion for fiber reinforced materials［J］．Composite Materials，1973，7(2):448-464．

［14］ Han K S，Hwang W．Cumulative damage models and multistress fatigue life prediction［J］．Composite Materials，1986，20(2):125-153．