接地導體球附近點電荷運動的討論
桑芝芳 鄭潔梅 黃楊
(蘇州大學物理科學與技術學院 江蘇 蘇州 215006)
接地導體球附近有點電荷存在,則導體球會發生靜電感應作用,導體球和點電荷間存在庫侖引力,我們可以用鏡像法求出球外空間電勢、電場的分布以及它們之間的相互作用力.若將點電荷從靜止釋放,點電荷將向接地導體球做變加速運動,越接近導體球,速度越大,甚至會出現超光速現象,此時應考慮相對論效應.
本文將考慮相對論效應,對接地導體球附近點電荷的運動情況進行討論,并和用經典力學處理該問題進行了比較.
1 理論分析
問題:設真空中有一半徑為R0的接地導體球,距球心a(a>R0)處有一質量為m的點電荷Q,若從靜止釋放,該點電荷運動情況如何呢?
分析:根據鏡像法,導體球表面的感應電荷對場的貢獻可以用假想的像電荷來代替,假設點電荷運動至距球心任意位置x處時,像電荷的位置和大小為
上式中b為像電荷到球心的距離,Q′為像電荷的電荷量,如圖1所示.球外空間的電場相當于點電荷Q和鏡像電荷Q′所激發的電場,此時點電荷Q所受作用力即為像電荷Q′對它的作用力,表達式為
(1)
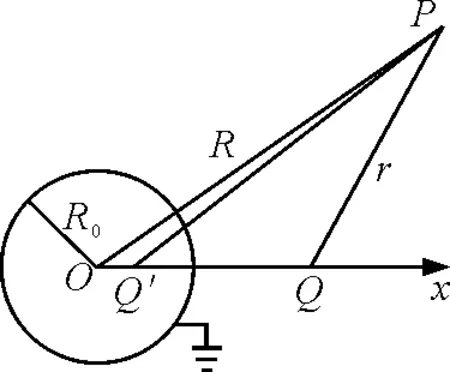
圖1
如果將點電荷Q從距離球心a處由靜止釋放,它將向導體球運動,此時像電荷的電荷量增大,與點電荷的距離減小,因而點電荷Q所受的作用力將迅速增大.
根據牛頓第二定律
F=ma
由式(1)可得
(2)
將式(2)分離變量,由初始條件t=0時,x=a,v=0,積分可得
可解得
(3)
式中負號“—”表示點電荷Q的運動方向與x軸方向相反,其中
由式(3)
分離變量,并應用初始條件得
從而可得點電荷Q從距離球心a處運動到任意位置x處的時間為
(4)
令x=R0,由式(4)即可得點電荷Q到達球面的時間.
但值得注意的是,當x→R0時,由式(3)可知v→-∞,速度發散,無物理意義.此時應考慮相對論效應,應用相對論力學求解.
根據相對論力學公式
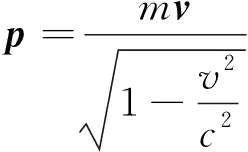
得
(5)
根據初始條件t=0時,x=a,v=0,并積分得
v=
(6)
當x→R0時,v→-c,即點電荷運動到球表面的極限速度為c,從而有效避免了速度的發散現象.
由式(6)進一步計算可得點電荷運動至球表面的時間為
(7)
2 數值討論
圖2給出了應用相對論力學和經典力學方法處理情況下,速度和位置的變化關系.
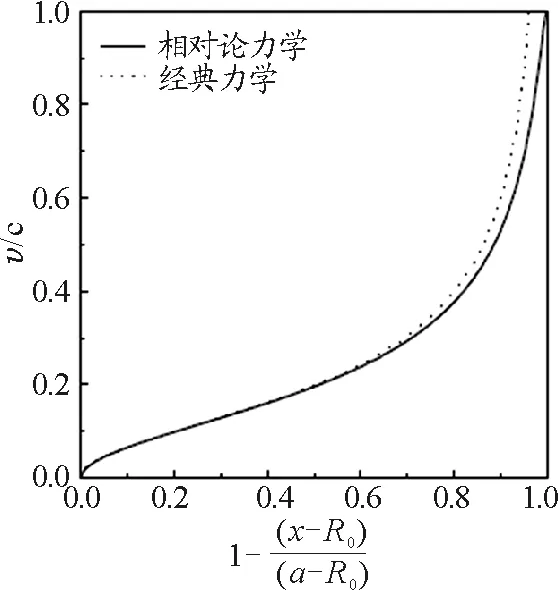
圖2 用兩種方法處理時,速度-位置的關系

圖3分別給出了應用相對論力學和經典力學方法處理情形下位置和時間的關系,其中
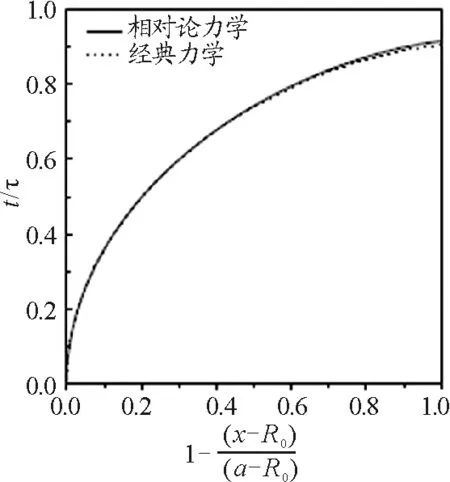
圖3 用兩種方法處理時,位置-時間的關系
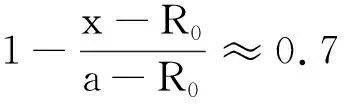
但值得注意的是,雖然用經典力學來求解點電荷到達導體球面的時間是有效的,并不意味著點電荷的運動就是完全的經典力學運動,我們應意識到其中的相對論效應.
參考文獻
1 郭碩鴻. 電動力學. 北京:高等教育出版社,1995
2 Kevin L. Haglin. Point charge dynamics near a grounded conducting plane.Am.J.Phys,2010,78(11):1190~1194

