淺析二元一次不定方程及其解

韓孝明

（呂梁學院汾陽師范分校，山西 呂梁 032200）

不定方程是數論中最古老的一個分支，也是數論中一個十分重要的研究課題，我國古代對不定方程的研究很早，且研究的內容也極為豐富，在世界數學史上有不可忽視的地位。如《張丘建算經》中的“百錢買百雞”問題、《九章算術》中的“五家共井”問題等等，中外馳名，影響甚遠。在公元3世紀初，古希臘數學家丟番圖曾系統研究了某些不定方程問題，因此不定方程也叫做丟番圖方程。

一、不定方程定義

所謂不定方程，是指未知數的個數多于方程的個數且其解受到某種條件的限制的方程或方程組。

不定方程領域中的基本問題是：不定方程有無整數解，有多少整數解，如何求出整數解。圍繞這些問題，至今存在著大量的未解決問題，因此不定方程仍是一個很活躍的數學領域。中小學的數學競賽也常常因為某些不定方程的解法巧妙而引入不定方程問題。

二、二元一次不定方程及其解

形如 ax+by=c(a，b，c∈z，ab≠0)的方程稱為二元一次不定方程。求其整數解的問題叫做解二元一次不定方程。

由于方程的解x、y可以是正整數，也可以是負整數，或者零，所以我們可以只討論a、b都是正整數的情況。例如，3x-2y=1與3x+2y=1的解相比較，y的值只差一個負號。

當 c=0時，如果(a，b)=d（a、b的最大公約數為 d），那么在方程的兩邊同時除以d,使x、y的系數互質。因此不妨假設(a，b)=1，解方程得x=-，由于(a，b)=1，因此當y能被a整除時，方程ax+by=0才有整數解。所以可令y=at（t為任意整數），這時x=-bt，即方程 ax+by=0的一切整數解為（其中t為任意整數）

當c≠0時，實際上也只需要討論c＞0的情況。因為當c＜0時，我們可以在方程兩邊同時乘以-1，這樣方程ax+by=c的右邊就成為正整數了。因此對于二元一次不定方程，可以只討論a＞0、b＞0、c＞0的情況。

現在我們研究二元一次不定方程在什么條件下才有整數解。先考察下面幾個方程有沒有整數解：2x+y=10，4x+2y=20，4x+2y=25。對于方程 2x+y=10，通過觀察可以知道，x=1,y=8是這方程的整數解，因此這個方程有整數解。

對于方程 4x+2y=20，方程兩邊同時除以2，得2x+y=10，因此這個方程也有整數解。

對于方程4x+2y=25，由于4x+2y=2(2x+y)為偶數，而25是奇數，因此這個方程沒有整數解。

對于方程2x+y=10來說，x、y的系數互質，上面已經指出這個方程是有解的；對方程4x+2y=20來說，雖然x、y的系數不互質，但它們的最大公約數2能整除20，這是方程也有解；對方程4x+2y=25來說，x、y的系數不互質，且它們的最大公約數2不能整除常數項20，這時方程無解。這些特點雖然是從一些具體的不定方程歸納出來的，但是它對一般不定方程也是適用的。我們有下面定理：

定理1：二元一次不定方程ax+by=c(a,b,c∈N*)有整數解的充要條件是d│c（其中d=(a,b）。

證明：一是必要性。如果方程ax+by=c有整數解x=x0，y=y0，則 ax0+by0=c，因為 d│a,d│b,所以 d│(a x0+by0),即 d│c。二是充分性。因為 d│c，所以 c=dq,由裴蜀恒等式可以知道，存在兩個整數x0，y0，使a x0+b y0=d。

在上式兩邊同時乘以 q，得 a x0q+b y0q=dq即a x0q+b y0q=c。

因此方程ax+by=c有整數解x=x0q,y=y0q。

由上述定理可知，如果c不能被a、b的最大公約數整除，那么方程ax+by=c無解，且可在ax+by=c兩端都約去d，使得(a，b)=1。所以通常二元一次不定方程的解是在a、b互質的情況下討論的。

判斷出一個二元一次方程有解以后，如何求出它的一切整數解呢？我們有下面的結論：

定理2：如果二元一次不定方程ax+by=c[(a,b)=1]有整數解x=x0，y=y0，則此方程一切解可以表示為

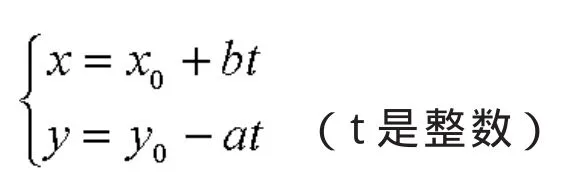
因為x=x0,y=y0是方程ax+by=c的整數解，所以ax0+by0=c，又因為 a(x0-bt)+b(y0+at)=ax0+by0=c。

再證明方程ax+by=c的任意一個整數解都可以表示成形式

設(x1,y1)是方程ax+by=c的任意一個整數解，則a x1,+b y1=c;

又由a x0+b y0=c，可得a(x1-x0)+b(y1-y0)=0，所以b│a(x1-x0)。

由于(a,b)=1，所以 b│（x1-x0），即 x1=x0+bt t∈z，所以 y1=y0-at t∈z。

由定理2可知，要求出二元一次不定方程ax+by=c的全部整數解，必須先求出它的一組特解。下面介紹幾種求ax+by=c特解的方法。

方法一，觀察法（或嘗試法）：

觀察法是根據已有經驗，通過觀察嘗試求解的一種辦法。

例如：方程2x+y=10很容易通過觀察得出x=1,y=8是其一組特解。

方法二，輾轉相除法：

輾轉相除法是利用求最大公約數的逆推過程求特解的一種辦法。

例如：解方程37x-107y=25。

解:因為(37,107)=1，1│25，所以此方程有解。

用輾轉相除法求特解107=37×2+33，37=33×1+4 33=4×8+1，從最后一個式子向上逆推，得到37×(-26)-107×(-9)=1，所以 37×(-26×25)-107×(-9×25)=25，

方法三，整數分離法：

整數分離法是用系數較大的未知數表示系數較小的未知數，從而求解的一種辦法。

例如：求方程7x+19y=213的一組解。

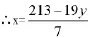
要使得x、y取整數，只需k取適當的值，使3-5k能被7整除。通過觀察與估算可知，當k取2時=-1。由此得x=30-2k=25。

因此，原方程的一組整數解是x=25，y=2。

方法四，同余法：

同余法是利用解同余式的方法求二元一次不定方程解的一種辦法。

例如：求9x+16y=35的解。

解：把原方程改寫成同余式16y≡35(mod6)，

解之，可得 y≡5(mod9)，所以 y=5+9t(t為任意整數)；

把y=5+9t代入原方程，得x=-5-16t，

綜上所述，僅是對二元一次不定方程及其解的初步認識，關于不定方程中還有很多未解之謎，望有興趣者共同探討。

[1]陳肇曾.數論初步[M].北京：高等教育出版社，1996.

[2]王元.初等數論[M].北京：人民教育出版社，2003.

[3]王進明.初等數論[M].北京：人民教育出版社，2002.