均勻腐蝕下管道可靠度及參數敏感度研究

劉慶剛，于新奇，彭培英

（河北科技大學機械電子與工程學院，河北石家莊 050018）

均勻腐蝕下管道可靠度及參數敏感度研究

劉慶剛，于新奇，彭培英

（河北科技大學機械電子與工程學院，河北石家莊 050018）

分別采用一次二階矩法和Monte-Carlo法對某存在均勻腐蝕的管道進行了可靠性分析，結果發(fā)現Monte-Carlo方法分析結果可靠度數值略低于一次二階矩法；可靠性分析發(fā)現，雖然管道的平均應力始終小于屈服應力，但管道可靠度隨著均勻腐蝕的發(fā)生呈現加速下降趨勢，至運行20年可靠度僅為0.58，已經無法安全使用；管道可靠性參數分析發(fā)現，對管道可靠度影響最大的為壁厚，其次為材料強度性能，然后為材料的載荷狀況，材料載荷對可靠度的影響程度取決于這種載荷對管道總體應力的貢獻程度。

均勻腐蝕；管道；可靠度；一次二階矩；Monte-Carlo

均勻腐蝕是化工管道及油氣長輸管道運行過程中常見的現象之一，也是造成管道失效的主要原因之一［1－2］。目前，在管道的設計中，一般將影響管道安全的各種參數當做定值，根據其應力水平進行強度設計。然而，在實際生產中，管道的尺寸、材料性能、載荷等不是定值，管道的外徑、壁厚等都存在偏差，管道材料的機械性能參數往往具有分散性，管道的內壓、拉力、彎矩等都可能由于某種原因而發(fā)生波動［3－4］，因此，在判斷管道安全狀態(tài)時，除了進行以應力水平為基礎的強度校核外，還需要進行可靠性分析。管道在均勻腐蝕條件下，除了應力水平的升高，其可靠度也將逐年下降，因此，有必要對管道在整個壽命周期內的可靠度進行研究，以判斷管道的運行安全狀態(tài)。

可靠度與管道的實際工作環(huán)境有關，設計環(huán)境、材料性能、管道尺寸等多方面參數均會影響管道的可靠度，因此，對管道可靠度影響參數的分析和研究對保障管道的安全具有一定的指導意義。

筆者分別采用一次二階矩法和Monte-Carlo法對存在均勻腐蝕的管道進行可靠性分析，同時對管道可靠度的影響參數的敏感性進行研究。

1 可靠度計算模型

采用應力－強度干涉模型［5］進行管道均勻腐蝕狀態(tài)的可靠性分析，如圖1所示。

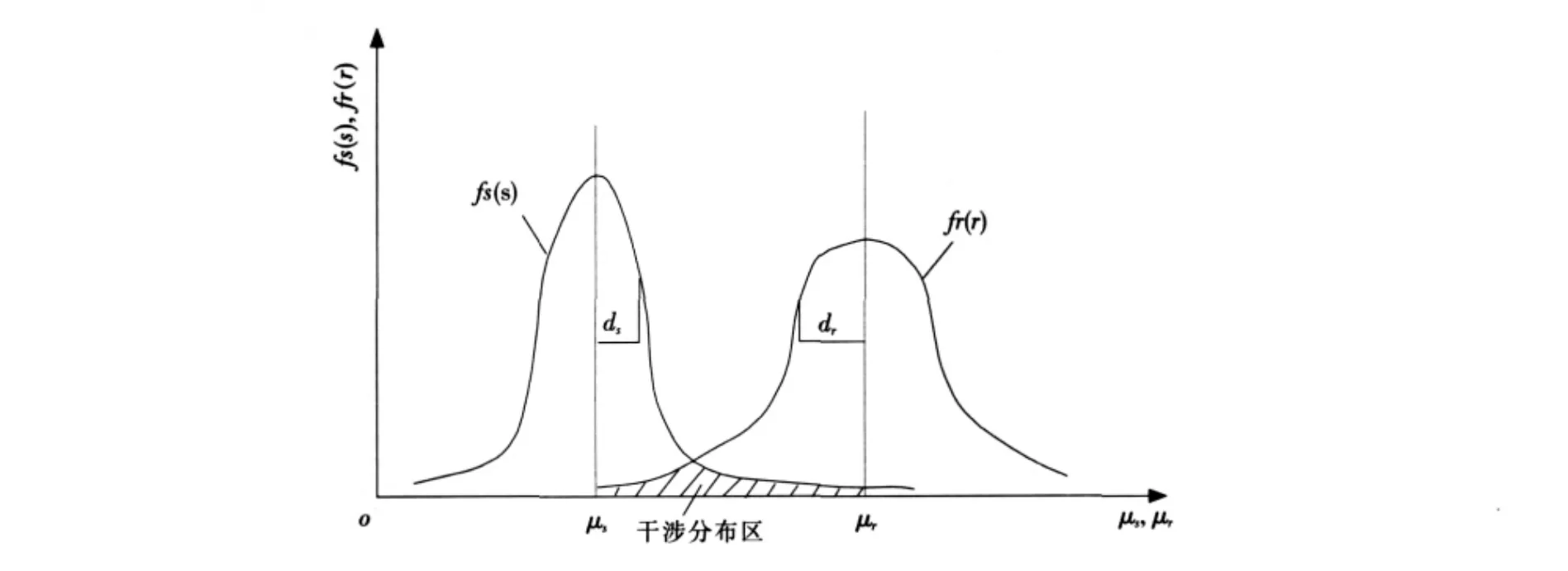
圖1 應力－強度干涉模型Fig.1 Stress-strength interference model

圖中，fs（s）表示應力概率密度函數，fr（r）表示強度的概率密度函數，只有當強度大于應力時，結構才是可靠的。因此，在這一模型下，將強度大于應力的概率定義為結構的可靠度系數β，

式中：β為結構可靠度系數；μs，μr為應力、強度均值；σs，σr為應力、強度標準差。

結構可靠度R可根據β查標準正態(tài)分布積累概率密度函數F N（0，1）得到，

一般情況下，應力和強度參數均為正態(tài)分布［6］。

可靠度的計算一般采用一次二階矩法［7］和Monte-Carlo法［8］，筆者分別采用2種方法計算，并對結果進行對比分析。

1.1 一次二階矩法

一次二階矩法是指將應力或者強度的計算公式按照Taylor級數基數展開來計算其均值和標準差的可靠性分析方法。

1.2 Monte-Carlo法

Monte-Carlo法是將隨機數賦予各種適當的物理意義，并建立模擬工程實際情況的概率模型，以將各種隨機過程的概率特征與數學分析問題的解答聯系起來。對于一些不容易構造成數學模型以進行可靠分析的復雜情況，應用Monte-Carlo法來求解較為有效。

在此計算過程中，獨立的隨機變量有X＝（x1，x2，…，x n），根據假定，這些變量均服從正態(tài)分布。則用Monte-Carlo法計算管道可靠度的步驟如下。

1）確定各獨立隨機變量的分布規(guī)律及其標準差；

2）生成［0，1］區(qū)間的均勻分布的隨機數，對各獨立隨機變量進行抽樣；

3）進行管道應力計算，根據剩余強度理論得到相應的失效模式，確定極限方程g（X）；

4）將各抽樣值代入狀態(tài)方程，檢驗是否滿足g（X）＞0；

5）重復步驟2）—步驟4）N次（N是隨機模擬總次數），累計g（X）＞0的次數N a；

6）計算管道的可靠度：P f＝N a／N，并輸出結果。

2 均勻腐蝕條件下管道可靠度計算

2.1 一次二階矩法

2.1.2 管道強度參數

強度r P為金屬的屈服極限σs，其均值為μσs，σs的標準差可以根據相應材料性能參數得到，一般為（0.05～0.10）μσs。

2.1.3 管道可靠度計算

將式（5）—式（7）代入式（1）、式（2）計算可得到管道的可靠度參數。根據上述過程編制相應計算機程序來完成可靠度的計算。

2.2 Monte-Carlo法

極限方程為g（X）＝σs－SP，按照1.2步驟編制計算機程序完成可靠度的計算。

3 管道應力及可靠度變化趨勢

分別采用一次二階矩法和Monte-Carlo法計算管道20年間的可靠度和應力情況，結果見圖2和圖3。

當各參數的標準差從0.01變化到0.2的過程中，分別采用一次二階矩法和Monte-Carlo法進行分析，得到不同均勻腐蝕程度的可靠度情況，見圖4—圖6。

4 結 論

1）一次二階矩法和Monte-Carlo法求解可靠度結果基本一致，說明2種方法均適用于管道均勻腐蝕條件下的可靠性分析；但Monte-Carlo法分析結果可靠度略低于一次二階矩法，這是因為一次二階矩法在運用Taylor公式展開式對高階項進行了截斷造成一定的誤差所致。

2）管道可靠度隨著均勻腐蝕而逐年加速降低，運行3.8年時可靠度仍保持在0.95以上；到8.6年時，可靠度保持在0.90以上；運行20年可靠度僅為0.58。

3）運行20年，管道平均應力水平依然小于材料屈服極限，但可靠度僅為0.58，說明管道的安全狀態(tài)不但需要考慮應力水平，還需考慮由于參數隨機性帶來的可靠性問題。

4）對管道可靠度參數分析發(fā)現，管道壁厚參數對可靠度影響最大，其次是材料屈服極限，然后是載荷參數。載荷參數的影響程度取決于對管道整體應力的貢獻程度（本例中彎矩影響最大，對總體應力水平的貢獻程度約為79%）。

5）在壁厚對可靠度影響程度的分析中，2種方法結果存在明顯不一致，這是因為管道應力方程對壁厚的一次偏導數過大，影響了一次二階矩法的分析精度造成的。當應用一次二階矩法進行可靠度分析時，需校驗各參數一階偏導，如一階偏導過大則不適合采用。

［1］何東升，郭 簡，張 鵬.腐蝕管道剩余強度評價方法及其應用［J］.石油學報（Acta Petrolei Sinica），2007，28（6）：125-128.

［2］羅 鵬，趙 霞，張一玲，等.國外天然氣管道內腐蝕直接評價案例分析［J］.油氣儲運（Oil ＆Gas Storage and Transportation），2010，29（2）：137-141.

［3］黃小光，韓忠英.海底管道疲勞損傷與疲勞壽命的可靠性計算［J］.油氣儲運（Oil ＆Gas Storage and Transportation），2010，29（11）：827-831.

［4］劉 鍇，鄭賢斌.在役油氣管道安全可靠性評估方法初探［J］.油氣田環(huán)境保護（Environmental Protection of Oil ＆Gas Fields），2010（12）：48-51.

［5］戴樹和，王明娥.可靠性工程及其在化工設備中的應用［M］.北京：化學工業(yè)出版社，1987.

［6］羅希延，趙榮國，蔣永洲，等.航空發(fā)動機渦輪盤用GH4133B合金常溫力學性能統(tǒng)計分析［J］.機械工程學報（Journal of Mechanical Engineering），2010，46（11）：75-83.

［7］羅文強，龔 玨，楊瑞琰.一次二階矩方法在斜坡穩(wěn)定性概率評價中的應用［J］.地球科學－中國地質大學學報（Earth Science-Journal of China University of Geosciences），1998，23（6）：639-642.

［8］張亦飛，王永新，王信棠，等.基于Monte Carle模擬的隧道圍巖組合分類法［J］.應用基礎與工程科學學報（Journal of Basic Science and Engineering），2009，17（2）：138-143.

Reliability of pipeline under uniform corrosion conditions and the sensitivity of the influence factors

LIU Qing－gang，YU Xin-qi，PENG Pei-ying
（College of Mechanical and Electronic Engineering，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

In this article First Order Second Moment method and Monte-Carlo methods are used to calculate the reliability of the pipelines under uniform corrosion conditions.The results show that the data obtained by Monte-Carlo is a little lower than that by First Order Second Moment.Reliability assessment also shows that the reliability is continuously decreasing while the stress of the pipeline is still lower than yield limit of the material.At the 20th year of the pipeline＇s use，the reliability is only 0.58，and the pipeline is not safe anymore.The parameters analysis of influence factors show that the thickness is the most important factor that influence the reliability，while yield limit is the second and load is the third.The influence of different loads to the reliability is decided by their awards to the total stress of the pipeline.

uniform corrosion；pipeline；reliability；First Order Second Moment；Monte-Carlo

TH114

A

1008-1542（2012）01-0040-04

2011-06-03；責任編輯：馮 民

劉慶剛（1981-），男，河北邢臺人，副教授，博士，主要從事化工設備與機械強度、安全評價及風險分析方面的教學研究。