圈C3的(r1，r2，r3)－冠都是優美的

吳躍生

(華東交通大學基礎科學學院，江西南昌 330013)

圈C3的(r1，r2，r3)－冠都是優美的

吳躍生

(華東交通大學基礎科學學院，江西南昌 330013)

討論了圈C3的(r1，r2，r3)－冠的優美性，用構造性的方法給出了圈C3的(r1，r2，r3)－冠的優美標號.證明了圈C3的(r1，r2，r3)－冠都是優美的.

圈;冠;優美圖

0 引言

本文所討論的圖均為無向簡單圖，V(G)和E(G)分別表示圖G的頂點集和邊集.

定義1［1］在圖G每個頂點都粘接了r條懸掛邊(r≥1的整數)所得到的圖，稱為圖G的r－冠.圖G的

1 －冠稱做圖G的冠.

定義2［2-12］V(G)=(v1，v2，…，vn)的每個頂點vi都粘接了ri條懸掛邊(ri≥0的整數，i=1，2，…，n)所得到的圖，稱為圖G的(r1，r2，…，rn)－冠，簡記為G(r1，r2，…，rn).特別地，當r1=r2=…=rn=r時，稱為圖G的r－冠.圖G的0－冠就是圖G.

定義3［1］對于一個圖G=(V，E)如果存在一個單射θ:V(G)→{0，1，2，…，E(G)}使得對所有邊e=(u，v)∈E(G)，由θ'(e)=θ(u)－θ(v)導出的E(G)→{1，2，…，E(G)}是一一對應，則稱G是優美圖，θ是G的一組優美標號，稱θ'為G的邊上的由θ導出的誘導值.

文獻［1］證明了圖P1∨Pn的優美性以及圖P1∨Pn的r－冠的優美性，并猜想:任意優美圖的r－冠都是優美圖.根據此猜想，文獻［13］－［14］證明了圈Cn(n≡0，3(mod 4))的r－冠是優美的，文獻［2］－［7］討論了當n=3，7，8，11，4 h，4h+3時，圈Cn的(r1，r2，…，rn)－冠的優美性.文獻［8］－［11］討論了一些圖ωn，m的(r1，r2，…，rn+m－1)－冠的優美性.文獻［12］、［15］、［16］討論了當n=3，4，5，6時Cn⊙k1的(r0，r1，r2，…，rn)－冠的優美性.本文討論了圈C3的(r1，r2，r3)－冠的優美性.

1 主要結果及其證明

定理1設V(C3)=(v1，v2，v3)，與vi鄰接的端點(或葉)記為xi，j(vi∈V(C3)，j=1，2，…，ri)，r1，r2，r3為任意自然數，圈C3的(r1，r2，r3)－冠都是優美的.

證明不妨設r2≥r3，定義圈C3的(r1，r2，r3)－冠的頂點標號θ為:

當rj=0時，xj，i=vj，j=1，2，3，i=1，2，…，rj，

(1)當r2＞r3時

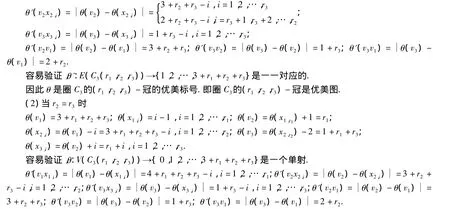
容易驗證，θ':E(C3(r1，r2，r3))→{1，2，…，3+r1+r2+r3}是一一對應.

因此θ是圈C3的(r1，r2，r3)－冠的優美標號.即圈C3的(r1，r2，r3)－冠是優美圖.

在定理1中，令r1=r2=r3=0，有

推論1C3的0－冠即圈C3是優美圖.

在定理1中，令r1=r2=r3=r，有

推論2圈C3的r－冠是優美圖.

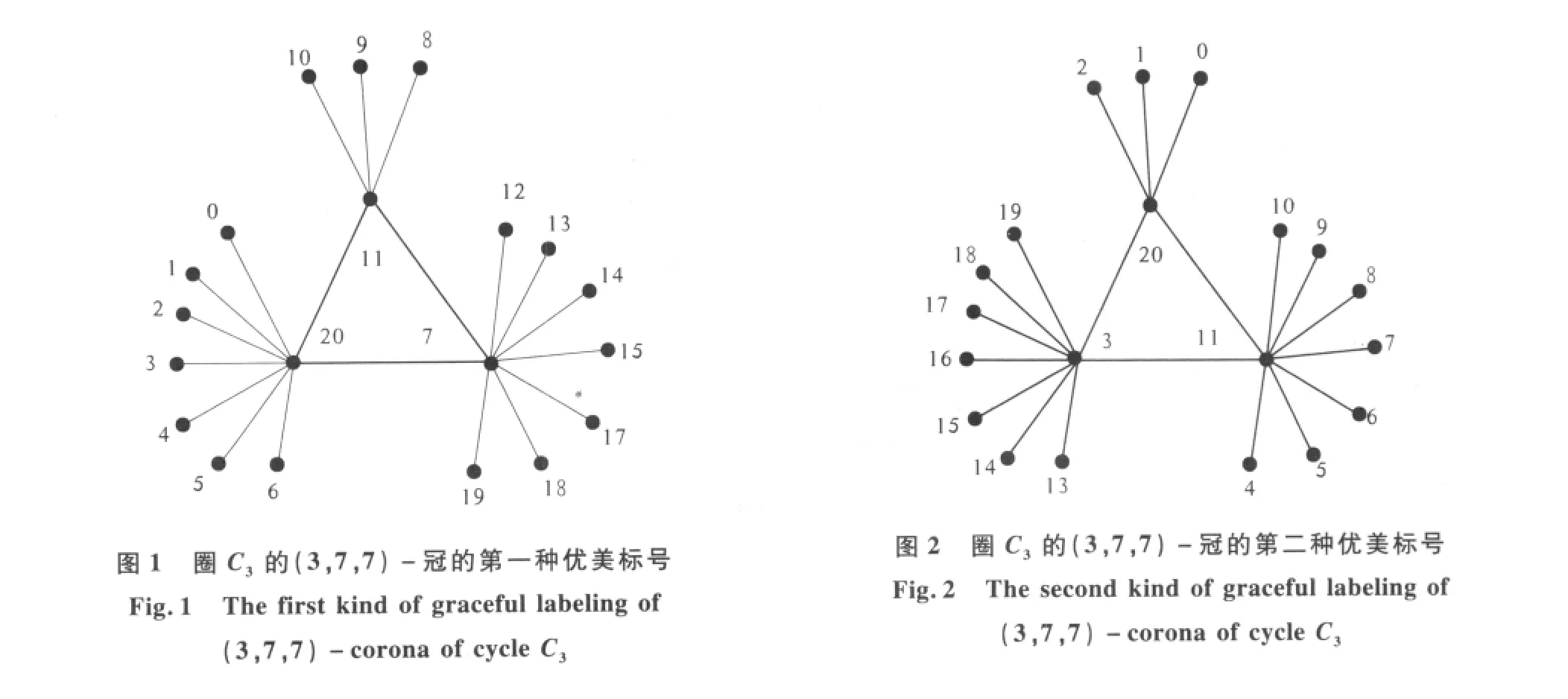
例1根據定理1，可以給出圈C3的(3，7，7)－冠的兩種優美標號(圖1、圖2).

［1］馬杰克.優美圖［M］.北京:北京大學出版社，1991.

［2］吳躍生，李詠秋.關于圈Cn的(r1，r2，…，rn)－冠(n=7，8)的優美性［J］.阜陽師范學院學報:自然科學版，2010，27(3):20－23.

［3］吳躍生，李詠秋.關于圈C11的(r1，r2，…，r11)－冠的優美性［J］.長春師范學院學報，2010，29(6):4－8.

［4］吳躍生，李詠秋.再探圈Cn的(r1，r2，…，rn)－冠(n=7，8)的優美性［J］.阜陽師范學院學報:自然科學版，2010，27(4):1－4.

［5］吳躍生，李詠秋.關于圈C3的(1，2a，2a+1)－冠的優美性［J］.河南教育學院學報:自然科學版，2010，19(4):1－2.

［6］吳躍生.關于圈C4h的(r1，r2，…，r4h)－冠的優美性［J］.華東交通大學學報，2011，28(1):77－80.

［7］吳躍生，李詠秋.關于圈C4n+3的(r1，r2，…，r4n)－冠的優美性［J］.吉首大學學報:自然科學版，2011，32(6):1－4.

［8］吳躍生，李詠秋.關于圖ω4，4的(r1，r2，…，r7)－冠的優美性［J］.宜春學院學報，2010，32(12):1－3.

［9］吳躍生，李詠秋.關于圖ω5，7的(r1，r2，…，r11)－冠的優美性［J］.嘉應學院學報，2011，29(5):5－8.

［10］吳躍生，李詠秋.關于圖ω5，6的(r1，r2，…，r10)－冠的優美性［J］.北京聯合大學學報，2011，25(2):60－6.

［11］吳躍生.關于圖ω4，6的(r1，r2，…，r9)－冠的優美性［J］.宜春學院學報，2011，33(8):1－3.

［12］康芳茂，吳躍生.關于C6⊙k1的(r0，r1，r2，…，r6)－冠的優美性［J］.懷化學院學報，2011，30(5):8－10.

［13］陳淑貞.關于回路的r－冠的優美性.海南師范學院學報，1997，10(1):29－31.

［14］胡紅亮.圖Cn及其r－冠的新的優美標號［J］.純粹數學與應用數學，2010，26(3):454－457.

［15］康芳茂，吳躍生.關于Cn⊙k1的r0(r0，r1，r2，…，rn)－冠(n=3，4)的優美性［J］.贛南師范學院學報，2011，32(6):25－27.

［16］吳躍生，李詠秋.關于Cn⊙k1的(r0，r1，r2，…，rn)－冠(n=5)的優美性［J］.喀什師范學院學報，2011，32(6):11－12.

The(r1，r2，r3)－Corona of Cycle C3Is Graceful

WU Yue-sheng

(School of Basic Science，East China Jiaotong University，Nanchang 330013，China)

The gracefulness of the(r1，r2，r3)－corona of the cycle C3is discussed.The graceful labeling is given.It is also proved that the(r1，r2，r3)－corona of the cycle C3is graceful.

cycle;corona;graceful graph

O157.5

A

1007－0834(2012)01－0015－02

10.3969/j.issn.1007－0834.2012.01.005

2011－12－26

國家自然科學基金(11061014);江西省自然科學基金(20114BAB201010);華東交通大學校立科研基金(11JC05)

吳躍生(1959—)，男，江西瑞金人，華東交通大學基礎科學學院副教授，主要研究方向:圖論.