基于虛擬體的身管多體動力學模型研究

陳世業，王良明，史 偉

（1.南京理工大學 能源與動力工程學院，南京210094；2.中國兵器工業基團051基地，陜西 華陰714200）

火炮進行射擊時，系統內構件間的剛性運動與彈性變形相互耦合，使身管產生復雜的彈性振動并形成炮口擾動，增大了射角的散布，嚴重影響火炮的射擊精度，因而建立相對準確高效的身管多體動力學模型，使其能較真實地反映復雜受力條件下炮口的動態響應特性，對火炮系統的動力學分析具有重要的指導意義.

從目前的研究狀況來看，柔性身管在系統模型中的描述主要采用模態法[1]、有限段法[2，3]、有限元法[4]等.在火炮的實際發射過程中，彈丸與炮膛內壁的接觸力以及燃氣作用力對身管的彈性振動產生的影響不容忽略，如何在反映身管彈性的前提下充分考慮彈丸的實時接觸力等外加載荷的作用，是身管建模過程中存在的一個重要問題.同時，由于彈丸和身管的接觸區域在隨時變化，即柔性體的邊界條件不斷改變，要獲得結構的動應力、動應變等信息，需通過完全有限元柔性體和多體動力學的耦合計算來實現，這大大降低了身管系統的求解效率.

針對上述問題，本文將虛擬體引入身管多體系統，提出了一種柔性身管的建模方法，推導了含虛擬體項的身管拉格朗日動力學方程，并結合算例驗證了方法的有效性.

1 系統描述

在此先引出本文中虛擬體的概念，即假想的無質量、無轉動慣量的剛性體.基于虛擬體構建的身管模型如圖1所示，模型中采用模態法描述身管的彈性變形，即將身管結構剛度通過預先有限元計算得到的模態來表示，通過模態振型的疊加來獲得其動態應力和應變.模型具體描述如下：虛擬體的幾何模型對應于身管的真實結構，由有限個虛擬體組成了身管的實體外形，虛擬體兩端以球鉸的形式聯接在經過模態解析的身管柔性單元上（圖1中為身管對應的變截面有限元梁單元），相鄰虛擬體間以剛性鉸約束限制其繞身管軸線方向的相對轉動，其中尾部段與炮尾鉸接.

有限個虛擬體的引入，使彈丸在由虛擬體組成的模擬身管中運動，從而把彈丸與柔性身管的接觸轉化為彈丸與虛擬體間的接觸碰撞，避免了由于接觸區域的變化而導致柔性體邊界條件改變這一問題；同時，彈炮間的相互作用力將通過虛擬體傳遞到柔性身管單元上，并反饋給彈丸運動，而由于單元中包含了身管真實結構所對應的模態信息，故能精確描述其動力學響應特性.

圖1 含虛擬體的身管幾何模型

2 虛擬體和相鄰柔性體間的運動學約束方程

取任意虛擬體j和其長度范圍的柔性體單元為第i個身管特征段，如圖2所示，OXYZ為系統的慣性參考系，OjXjYjZj、OmXmYmZm和OnXnYnZn分別為虛擬體j和柔性體單元m、n的連體坐標系，原點位于質心處.在多體動力學分析中，剛性鉸約束和基于有限元的柔性鉸約束已經很完善，在此只列出虛擬體和其鉸接的柔性體間的約束方程.虛擬體j的坐標系原點可表示為

式中，A為柔性體參考坐標系的姿態矩陣和分別為剛體上一點相對剛體參考坐標系的未變形矢量和變形矢量，節點位置的變形矢量可以表示為振型的線性組合：

虛擬體j的姿態方程為式中，f代表柔性體，Am，j為未變形狀態柔性體m和虛擬體j間的姿態矩陣為由轉動變形引起的相對姿態矩陣，且為旋轉變形矢量εm的函數，εm的表達式為

圖2 身管特征段幾何描述

聯立式（1）、式（3），可以得到柔性體坐標系和虛擬體坐標系間的運動約束：

式中，（I1I2I3）為3×3的單位矩陣和分別為位置約束和角約束.對上式進行變形：

3 身管多體動力學方程

在第i個身管特征段中，取虛擬體j和柔性體m為新的單元體k，其動能Tk和彈性勢能Uk的表達式為

單元體的質量矩陣Mk為

式中，nf為模態坐標的個數.

由于虛擬體的運動不會產生應變能，單元體的剛度矩陣Kk在柔性體m的節點坐標系中產生.用拉格朗日乘子法建立單元體k的運動微分方程為

式中，λ為拉格朗日乘子；廣義力Fk包括單元彈性變形引起的廣義力和外加載荷引起的廣義力兩部分，其中包括了彈炮接觸作用引起的廣義力.將單元體的動能表達式代入微分方程可以得到：

當彈丸與虛擬體j發生接觸碰撞，兩者間的接觸力FR轉化為柔性體單元m、n中的節點力FR，m、FR，n，如圖3所示.

圖3 彈丸與身管特征段的幾何模型

在單元體k中，由接觸引起的廣義力FkR為

同時，限制相鄰虛擬體間繞身管軸線方向的相對轉動，即在機構的約束方程中添加虛擬體間的剛性鉸約束

綜上，將組成身管多體系統的n個構件產生的運動方程與系統約束方程C（q，t）聯立，得到系統動力學方程的統一矩陣形式：

由上式可知，身管系統的質量矩陣M和約束矩陣Cq中均含有虛擬體項，其中Cq由三部分組成，包括柔性體與虛擬體間的約束、柔性體間的約束和相鄰虛擬體間的約束.當彈丸與虛擬體發生接觸碰撞時，兩者的相互作用力通過廣義力Fe的形式傳遞到系統的動力學方程中，最終對身管的彈性振動產生影響并反饋給彈丸運動.

4 算例分析

4.1 基本仿真條件

以某型履帶式自行火炮為例，引入身管多體動力學模型，如圖1所示.考慮剪切力和轉動慣量對身管彎曲變形產生的影響，基于Timoshenko梁理論[6]建立身管的變截面有限元梁單元，采用Block Lanczos數值法，對模態實施求解，由于身管的高階模態對系統振動影響較小[7]，在實際計算過程中可取有限個低階模態進行分析，本文取其前10階固有振動模態，如表1所示.模型中由11個虛擬體組成模擬身管，附加了22個柔性鉸和11個剛性鉸約束，含模態信息的柔性身管梁單元在炮閂前端面中心處與炮尾固連，其中身管阻尼設為剛度系數的0.003倍.

表1 某自行火炮身管前10階模態的振動頻率和振動周期

4.2 結果與分析

試驗條件如下：自行火炮處于水平土壤地面上，高低射角10mil，方向射角8 mil，采用全裝藥底凹榴彈在常溫下進行射擊，系統模型采用上述邊界條件進行計算分析.

火炮在t＝0.05s時射擊.圖4、圖5給出了后坐位移l和后坐速度v的對比情況，可以看出計算曲線和試驗曲線基本吻合.

圖4 炮尾后坐位移對比曲線

圖5 炮尾后坐速度對比曲線

由圖4可知，計算曲線中炮尾在0.62s復進到位，相對于測試值0.64s提前0.02s，主要是由于對身管進行有限元分析時，建立的變截面梁模型簡化了身管的真實幾何結構，造成質量、轉動慣量和質心位置與實際值有所偏差.

炮口的動態響應取炮口點的振動角位移為研究對象，圖6、圖7分別給出了垂向角位移和水平方向角位移的對比結果.彈丸經過0.011s（t＝0.061s）出炮口，從圖中可以看出，該時刻附近計算所得的角位移分量和測試值有很好的一致性.

圖6、圖7中測試曲線和計算曲線分別在0.64s和0.62s時發生比較大的波動，這是由于炮尾復進到位時對應的復進速度并不為0，這是它與搖架發生碰撞所造成的.

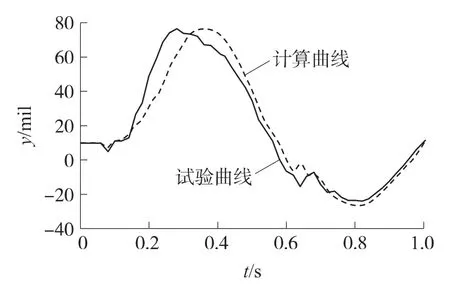
圖6 炮口點垂向振動角位移對比曲線

圖7 炮口點水平方向振動角位移對比曲線

圖8給出了彈丸速度vd的計算曲線，可知彈丸初速為706m/s，而實測彈丸初速713m/s，兩者的相對誤差為0.98%，可知彈丸在虛擬身管中的運動與實際情況符合較好.

圖8 彈丸速度計算曲線

5 結論

本文將提出的柔性身管建模方法應用到某履帶式自行火炮的動力學模型中，通過計算結果和試驗數據的對比，得到如下結論：

① 把虛擬體引入到柔性身管的建模中在理論上是可行的，可以為彈炮耦合問題的研究提供一定參考.

②采用該方法建立的身管模型，充分考慮了彈丸接觸力等外加載荷的影響，并能在復雜受力條件下較為精確地描述身管的彈性振動和火炮的炮口擾動.

[1]徐達，胡俊彪，穆歌.基于剛柔耦合的坦克炮發射動力學仿真分析[J].裝甲兵工程學院學報，2009，23（4）：45－47，51.XU Da，HU Jun－biao，MU Ge.Simulation analysis on tank gun firing dynamics based on rigid－flexible coupling[J].Journal of Academy of Armored Force Engineering，2009，23（4）：45－47，51.（in Chinese）

[2]劉雷，陳運生.身管多體動力學模型研究[J].南京理工大學學報，2005，29（3）：267－269，295.LIU Lei，CHEN Yun－sheng.Multi－body dynamic model of barrel[J].Journal of Nanjing University of Science and Technolo－gy，2005，29（3）：267－269，295.（in Chinese）

[3]王曉鋒，姜興渭.有限段法在高炮發射多體系統動力學分析中的應用[J].南京理工大學學報，2001，25（1）：25－27.WANG Xiao－feng，JIANG Xing－wei.Application of finite segment method to dynamic analysis of antiaircraft gun launch[J].Journal of Nanjing University of Science and Technology，2001，25（1）：25－27.（in Chinese）

[4]于存貴，申亮，馬大為.艦炮剛柔耦合發射動力學研究[J].系統仿真學，2009，21（23）：7 694－7 696.YU Cun－gui，SHEN Liang，MA Da－wei.Study on simulation for rigid－flexible coupling launch dynamics of naval gun[J].Journal of System Simulation，2009，21（23）：7 694－7 696.（in Chinese）

[5]馮勇，馬大為，薛暢，等.多管火箭炮剛柔耦合多體發射動力學仿真研究[J].兵工學報，2006，27（3）：545－548.FENG Yong，MA Da－wei，XUE Chang，et al.Simulation studies of coupled rigid and flexible multi－body dynamics for multiple launch rocket systems[J].Acta Armamentarii，2006，27（3）：545－548.（in Chinese）

[6]EISENBERGER M.Dynamic stiffness matrix for variable cross－section Timoshenko beams[J].International Journal for Numerical Methods in Biomedical Engineering，1995，11（6）：507－513.

[7]余成寶.火炮系統模態測試與分析[D].南京：南京理工大學，2007.YU Cheng－bao.Modal test and analysis of artillery system[D].Nanjing：Nanjing University of Science and Technology，2007.（in Chinese）