基于粘聚區模型的推進劑開裂數值仿真

韓 波，鞠玉濤，許進升，周長省

（南京理工大學 機械工程學院，南京210094）

固體火箭發動機裝藥在生產、運輸和使用過程中會承受到各種復雜載荷的作用，在這些載荷作用下裝藥表面可能會產生微裂紋，裂紋的萌生和發展會影響發動機內彈道性能和發動機的使用安全性，因此建立推進劑裂紋擴展過程的數值仿真方法十分重要.目前國內針對推進劑斷裂過程的數值仿真尚不能準確模擬裂紋擴展過程中的應力分布、裂紋走向和裂紋終止問題.目前模擬材料裂紋擴展過程有虛擬裂紋閉合技術（VCCT）、擴展有限元法（XFEM）和粘聚區模型（CZM）等多種方法.VCCT需要事先設定材料的裂紋擴展路徑，后兩者可以模擬裂紋走向未知情況下的裂紋擴展問題.CZM是一種基于能量平衡和材料損傷的裂紋擴展模型，裂紋在擴展過程中裂尖材料產生損傷，其力學性能下降，當裂紋消耗能量等于裂紋擴展能時，裂尖材料失效擴展.裂尖材料的損傷避免了裂尖應力的奇異性.國外自20世紀90年代開始在粘聚區模型方面開展了大量的研究工作，國內相關學者近幾年也開始展開相應的研究工作[1，2].本文使用粘聚區模型建立復合固體推進劑裂紋開裂過程的物理和數學模型，并結合ABAQUS用戶自定義單元開發技術實現對復合固體推進劑裂紋擴展過程的數值仿真，以期為推進劑裝藥結構完整性及安全性分析提供理論支持.

1 物理數學模型

1.1 粘聚區本構模型

粘聚區模型的提出起源于DUGDALE的條狀屈服區模型和BARENBLAT提出的內聚力模型.隨著粘聚區理論的發展，之后又提出了各種形式的裂尖粘聚區應力分布模型，并且在瀝青、金屬等材料上取得了成功應用.粘聚區模型（圖1所示）中材料的實際裂尖位于裂尖損傷位移δc處，假設的損傷裂尖位于損傷應力最大處.為了準確描述裂尖的損傷應力變化情況，需要建立裂尖損傷應力和損傷位移之間的對應關系——粘聚區模型本構.

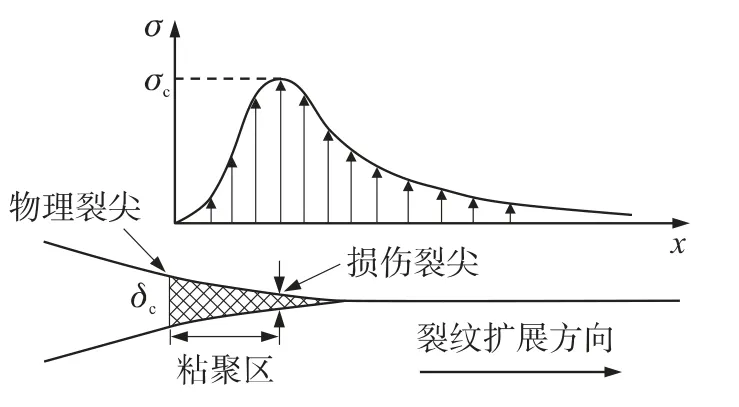
圖1 粘聚區模型示意圖

國外有許多學者提出了不同的粘聚區本構形式，主要有指數勢函數形式、多項式形式、線性形式.其中線性粘聚區本構通過合理調整本構參數可以有效避免人工柔量問題，并且在粘彈性瀝青材料上獲得了成功應用[3，4].圖2為線性粘聚區模型示意圖.在二維情況下，材料裂尖非線性區的裂紋張開有效位移和有效應力定義為

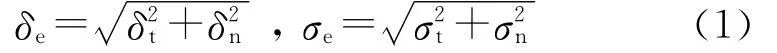
式中，δt和δn為裂尖的切向和法向位移，σt和σn為裂尖的切向和法向應力.線性粘聚區模型中假設有效位移和有效應力關系呈現為2個線性階段，如圖2所示，其中σmax為材料的應力損傷初始值；δcc為材料的損傷初始位移；δc為材料開裂的最終擴展位移；Gc為材料的斷裂能，即圖2中三角形面積.當裂尖材料的有效應力σe達到損傷應力σmax后，材料承載能力下降，當裂尖材料總擴展位移達到δc時，其消耗的能量等于材料的斷裂能Gc，之后材料發生完全斷裂.

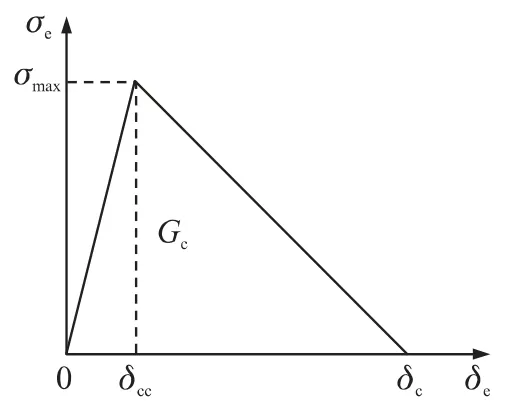
圖2 線性粘聚區本構示意圖

線性粘聚區本構的具體表達形式為

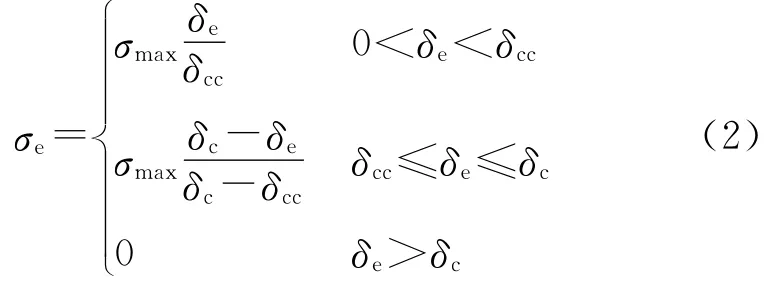
粘聚區模型的引入使有限元模型中增加了人工柔量項，造成了整體結構剛度下降.為了便于討論，以圖3所示的結構為例，上下為2個正常的實體單元，中間加入粘結單元.實體單元初始長度為d，粘結單元初始厚度為0.在載荷F作用下單元沿上下方向伸長，實體單元伸長Δ，粘結單元伸長Δc.設實體單元和粘結單元剛度分別為Ks和Kc，Es為實體單元的模量.

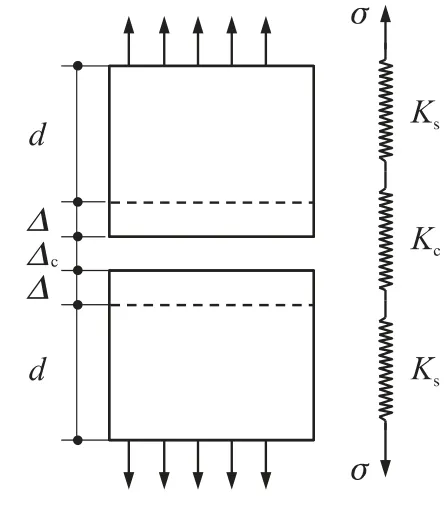
圖3 粘結單元柔量分析示意圖

在粘結單元未損傷前，由力平衡方程可得：

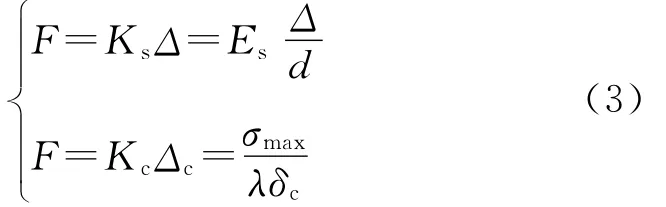
式中，λ＝δcc/δc，該結構的整體剛度為

不加粘結單元的理論剛度為Ki＝Ks/2，由式（3）、式（4）得：

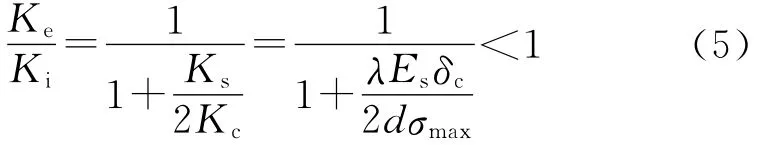
從式（5）可以發現，整體剛度與基體材料的模量Es、網格大小d、粘聚區本構參數δc、σmax和λ相關，其中Es，δc和σmax為材料的固有屬性，不可改變.增大網格可以增大系統的剛度，但是會造成計算精度的下降.λ表征了粘聚區本構中初始上升段的斜率，通過減小λ可以提高粘結單元的初始剛度，從而有效避免過大的人工柔量帶來的問題.λ的選擇可以通過加入粘結單元和未加入粘結單元情況下的仿真結果對比確定，λ的取值應保證粘結單元的加入不會對材料未產生損傷前的系統剛度產生較大影響，從而保證計算模型具有合理的精度.

1.2 推進劑本構模型

HTPB推進劑是一種典型的粘彈性材料，在推進劑裝藥結構完整性分析中廣泛采用線性粘彈性本構模型，該模型可以較好地反映推進劑的力學特性，因此本文在計算中使用線粘彈性本構模型.線粘彈性材料的本構方程可以寫成：

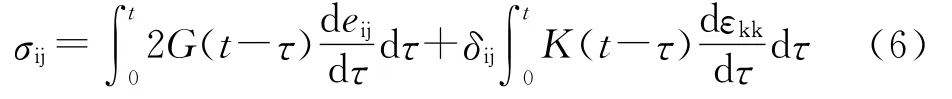
式中，G（t）和K（t）為剪切模量和體積模量，可表示為

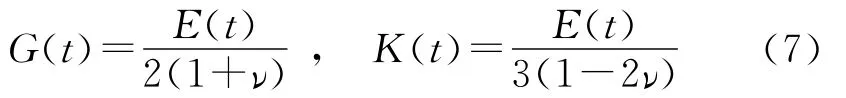
式中，E（t）為楊氏松弛模量，ν為泊松比.E（t）可以寫成Prony級數的形式：

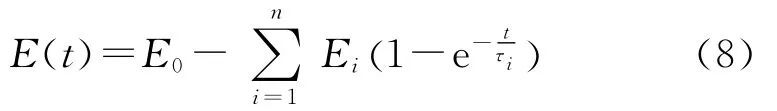
式中，τi為Prony級數中的松弛時間.

2 有限元離散及仿真方法研究

ABAQUS提供了豐富的材料和單元庫，但是ABAQUS材料和單元庫中并不包含特定粘聚區模型和本構關系，需要用戶進行開發.ABAQUS提供了用戶自定義單元的接口程序UEL，用戶可以根據需要自定義各種新單元.下面以二維粘聚區模型為例，給出ABAQUS二次開發所需增量形式的粘聚區單元建立過程.由有限元理論可知，利用Newton－Raphson法求解非線性有限元問題時需要給定單元的切線剛度矩陣KT和節點平衡矢量列陣R.

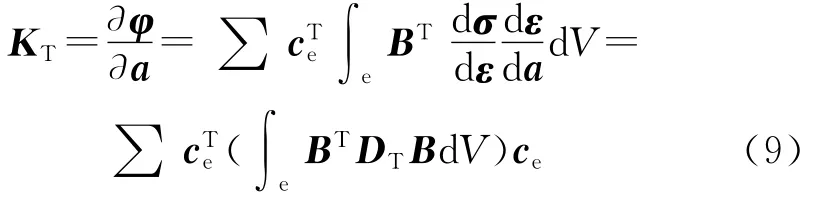
Newton法的迭代公式為

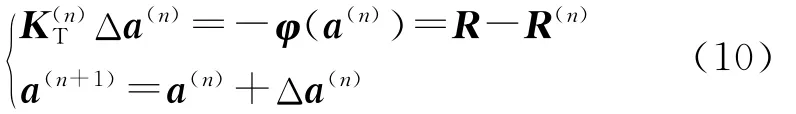
式中，

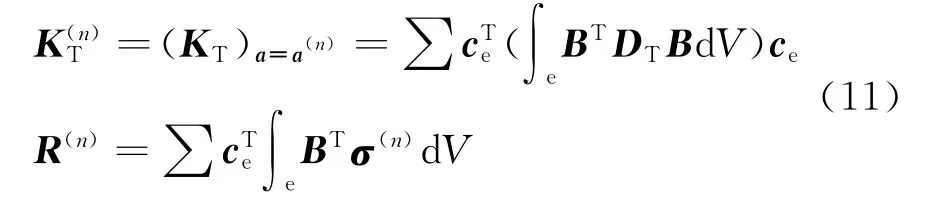
式中，ce為單元選擇矩陣，a為單元位移向量，V為被積單元體積，σ為單元應力.

材料的Jacobian矩陣定義為

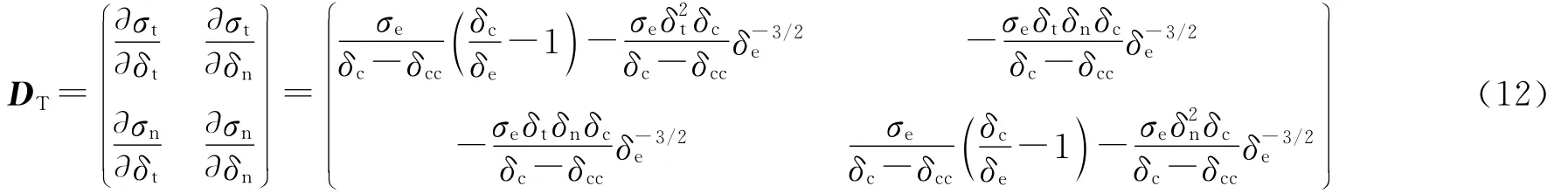
圖4為2個平面三角形單元和一個粘結單元變形示意圖.

單元節點1、4和2、3之間的相對位移為

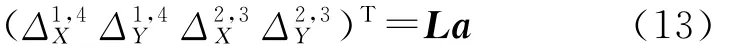
單元的積分點法向和切向位移表示為

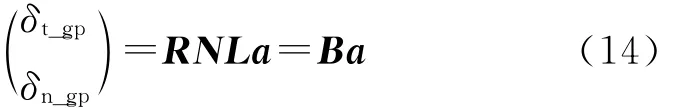
式中，a為圖3中節點在系統坐標下的坐標值，R為坐標轉換矩陣，N為插值形函數.

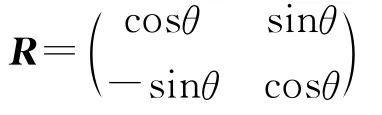
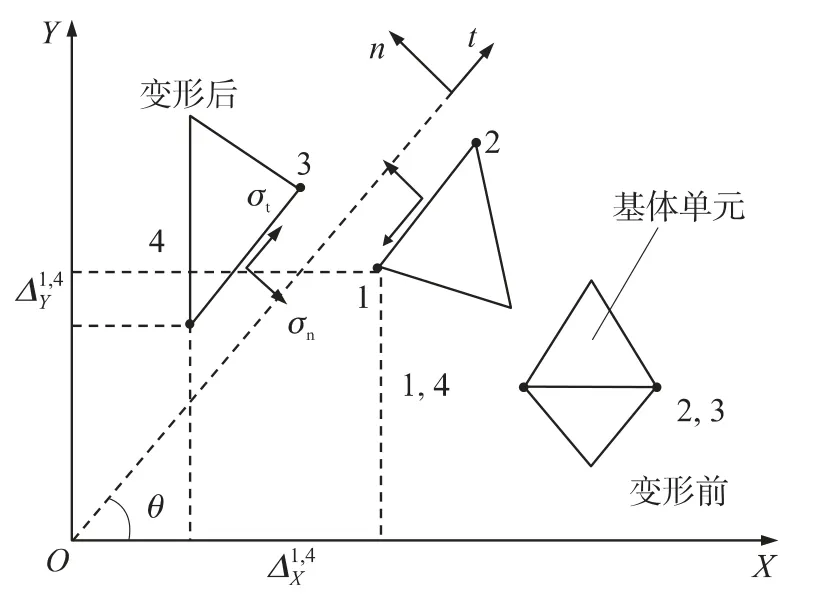
圖4 粘結單元

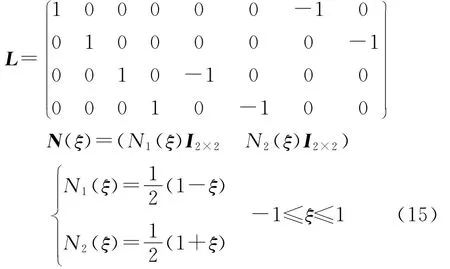
式中，ξ為變換后的坐標.

本文根據上述數學模型編制了ABAQUS用戶自定義單元開發程序UEL，建立了復合推進劑裂紋擴展數值仿真方法.

3 仿真與分析

3.1 仿真模型

為了驗證本文所建立的仿真計算方法的可行性，利用文獻[6]中的模型，對 HTPB推進劑Ⅰ－Ⅱ型裂紋進行了數值仿真計算，圖5為仿真模型示意圖.模型寬度W＝50 mm，長度H＝100 mm，中心裂紋長度l＝20mm.藥柱下表面固定，上表面施加60mm/min等速拉伸載荷.HTPB推進劑松弛模量通過松弛實驗獲取，Prony級數參數見表1，初始模量E0＝15 MPa，泊松比取0.499.粘聚區本構使用式（3）所示的形式，本文主要研究 HTPB復合推進劑的裂紋擴展有限元計算方法，粘聚區本構參數的具體實驗獲取不在本文研究范圍之內.根據單軸拉伸實驗，裂尖損傷應力σmax大致取0.5 MPa，推進劑斷裂能Gc根據文獻[5]大致取500J/m2.

圖5 仿真模型示意圖

表1 松弛模量數據

使用粘聚區模型模擬裂紋擴展方向未知情況下的材料開裂過程需要在正常實體單元之間加入粘結單元，通過ABAQUS CAE無法實現.本文采用MATLAB編程語言生成包含粘結單元和二維實體單元的有限元網格.如圖6所示，生成的網格中包含10 475個粘結單元和7 052個三角形實體單元.為了準確模擬裂紋擴展過程中的應力、應變變化情況，在預測的裂紋擴展路徑四周進行了網格細化.

圖6 有限元網格

3.2 仿真結果分析

為了確定合理的λ以避免人工柔量的影響，本文對比了無粘結單元情況下和加入了粘結單元情況下的仿真計算結果，如圖7所示，圖中，Fs為圖6中有限元模型計算的上下表面拉力.

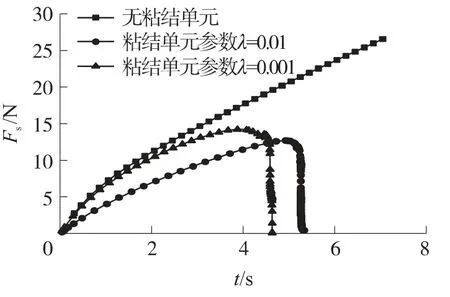
圖7 不同λ下的載荷－時間曲線

從圖7可以發現λ的值明顯影響了計算所得的載荷－時間曲線.當不插入粘結單元時，載荷隨時間持續上升，推進劑不會產生斷裂.粘結單元的引入可以計算出推進劑從裂尖產生局部損傷直至斷裂的整個過程.當λ＝0.01時，從圖上可以看出粘聚區模型計算結果和無粘聚區模型下的計算結果相差很大，其裂紋未擴展前的曲線斜率明顯低于后者，這是由于過大的人工柔量導致了系統剛度的下降.當λ＝0.001時，在3s之前粘聚區模型的使用與否對計算結果影響不大，說明該值可以較好地反映粘聚區本構模型和裂紋擴展的基本規律.在3s之后由于推進劑裂尖損傷的產生，材料承載能力開始下降，此時常規有限元方法已經不能反映出裂紋的擴展過程.在4.56s時載荷達到最大值，之后推進劑失穩快速開裂.

圖8和圖9為在λ＝0.001情況下，3.07s和4.56s時的有限元網格變形情況.在3.07s時推進劑裂尖開始產生了應力損傷情況，此時裂紋將要產生擴展，損傷裂尖位于裂尖的初始位置.從圖7上可以看出4.56s時仿真模型所受到的載荷達到最大值.對比圖9，發現推進劑產生了明顯的擴展裂紋，損傷裂尖位置基本上達到了推進劑的邊緣，此時推進劑的真實裂尖并不位于損傷裂尖，推進劑仍能承受外載荷的作用，但是與未受損傷前相比其承載能力已經明顯下降.

圖8 3.07s有限元網格

圖9 4.56s有限元網格

圖10為仿真和文獻[6]中實驗獲得的拉伸破壞后的HTPB推進劑裂紋擴展路徑.通過實驗獲得的初始裂紋起裂角平均值為51.9°，之后裂紋擴展方向轉變為平直裂紋，而仿真所獲得的初始裂紋起裂角約為62°，之后裂紋轉變為平直裂紋.由于粘聚區有限元仿真中裂紋沿單元界面開裂，裂尖的網格細密程度決定了仿真獲得的初始裂紋擴展角精度.本文仿真所獲得的初始裂紋擴展角與實驗結果的差距部分主要是由裂尖網格劃分精度導致.

圖10 仿真和實驗開裂路徑

文獻[6]中觀察到“裂紋初始擴展后都有向橫向裂紋的轉變趨勢”，仿真結果也出現裂紋初始擴展之后轉變為橫向裂紋的現象.圖10中的裂紋擴展路徑基本重合，表明粘聚區模型可以較好地預測HTPB復合裂紋的裂紋擴展路徑.

圖11為裂紋擴展路徑上距離初始裂尖不同位置處的Von Mises應力－時間曲線，所示的幾條曲線均呈現出先增大后減小的形狀，曲線的峰值對應損傷裂尖到達該點的時間.從圖上可以看出裂尖位置隨時間的變化情況，圖中4個位置達到應力最大值的時間間隔呈現出逐漸縮小的趨勢，這說明裂紋呈現出加速擴展的趨勢.

本文建立了一種復合固體推進劑開裂過程數值仿真方法，為了能更加準確地描述出復合推進劑的裂紋擴展過程，需要通過大量的實驗建立起準確的推進劑粘聚區模型，這也是筆者下一階段的工作目標.

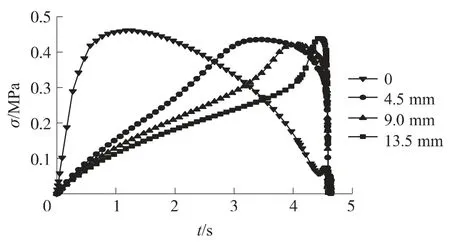
圖11 裂尖擴展路徑上不同位置的應力－時間曲線

4 結論

本文采用粘聚區模型理論針對復合固體推進劑裂紋擴展過程進行了研究，建立了針對推進劑斷裂過程的物理和數學模型，并編制了ABAQUS二次開發程序，實現了對固體推進劑Ⅰ－Ⅱ型復合裂紋擴展過程的數值仿真計算，得到了如下結論：

①使用粘聚區模型可以很好地模擬出復合固體推進劑裂尖的損傷應力場、裂紋擴展路徑和裂紋體開裂過程.

②粘聚區模型可以為固體推進劑裝藥完整性和安全性分析提供一種可靠的分析計算方法.

[1]劉陸廣，歐卓成，段卓平，等.混凝土動態斷裂數值模擬[J].兵工學報，2010，31（6）：741－745.LIU Lu－guang，OU Zhuo－cheng，DUAN Zhuo－ping，et al.Simulation of concrete dynamic fracture[J].Acta Armamentarii，2010，31（6）：741－745.（in Chinese）

[2]崔浩，李玉龍，劉元鏞，等.基于粘聚區模型的含填充區復合材料接 頭 失 效 數 值 模 擬 [J].復 合 材 料 學 報，2010，27（2）：161－168.CUI Hao，LI Yu－long，LIU Yuan－yong，et al.Numerical simulation of composites joints failure based on cohesive zone model[J].Acta Materiae Composite Sinica，2010，27（2）：161－168.（in Chinese）

[3]SONG S H，PAULINO G H，BUTTLAR W G.A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material[J].Engineering Fracture Mechanics，2006，73（18）：2 829－2 848.

[4]SONG S H，PAULINO G H，BUTTLAR W G.Simulation of crack propagation in asphalt concrete using an intrinsic cohesive zone model[J].Journal of Engineering Mechanics，2006，132（11）：1 215－1 223.

[5]MAROM G，HAREL H，ROSNER J.Fracture energies of composite propellants[J].Jounal of Applied Polymer Science，1977，21（6）：1 629－1 634.

[6]張亞，強洪夫，楊月誠.國產 HTPB復合固體推進劑Ⅰ－Ⅱ型裂紋斷裂性能實驗研究[J].含能材料，2007，15（4）：359－361.ZHANG Ya，QIANG Hong－fu，YANG Yue－cheng.Fracture behavior of HTPB composite propellant inⅠ－Ⅱ mixed mode crack[J].Chinese Journal of Energetic Materials，2007，15（4）：359－361.（in Chinese）