常見群樁排列方式淺析
毛穗豐,康 東,王 宏
(中國水電顧問集團成都勘測設計研究院,四川 成都 610072)
1 前 言
當今連續剛構橋型修建得比較多,特別是跨度在100~200m時,只要地形條件合適,首選的橋型一般都是連續剛構。此類橋型,當橋墩不高時(一般在70m以下),一般采用雙肢薄壁墩;當橋墩在70m以上時,采用箱型整體式的比較多。但不管采用哪種橋墩形式,除了擴大基礎外,比較常見的是采用承臺加群樁的基礎型式,且樁基的根數一般不小于4。當樁數為n2時,樁基一般按縱橫向對稱排列,即按n×n的形式排列;但若不滿足時,其排列方式則值得研究。以下主要介紹此類群樁的排列方式。
2 群樁的排列方式
群樁指在水平外力作用平面內有一根以上的樁的樁基礎,群樁多與承臺固結為一整體,共同受力。常見的群樁一般均有4根及以上的樁,其排列的方式也有多種,有縱橫直線排列的,也有梅花形布置的。具體布置形式見圖1(由于7根樁的形式很罕見,故圖中未示此布置)。
以上幾種常見的群樁排列方式,其共同點是樁基及承臺均關于x軸與y軸對稱布置,不同點是A、B、E排列由于承臺為正方形,樁基排列完全對稱(此時假定xi=yi),此種情形比較簡單,不再過多論述。但是當樁基承臺為C、D特別是常見的C中(1)、(2)與D中(3)、(4)布置時,此時由于承臺長邊較短邊長得多,樁基的排列就值得探討了。
3 承臺樁基豎直力計算
為了研究以上樁基承臺中群樁的排列采用C中(1)與(2)以及D中(3)與(4)哪種更為合理,即在相同的前提條件下,哪種群樁的布置方式使樁基產生的最大豎直力更小,即認為是更合理的,這樣在橋梁的設計中可減短樁長,降低橋梁造價。為此,先來探討樁基豎直力的計算。計算圖示見圖2,計算公式見式(1)。
(1)
式中Nid——第i根樁的單樁豎向力設計值;
Fd——由承臺底面以上的作用(或荷載)產生的豎向力組合設計值;
Mxd、Myd——由承臺底面以上的作用(或荷載)繞通過樁群形心的x軸、y軸的彎矩組合設計值;
n——承臺下面樁的總根數;
xi、yi——第i排樁中心至y軸、x軸的距離。
由上式可知,當公式等號后面兩項均取正值即“+”時,此時樁承受的豎直力最大,即與Mxd、Myd轉動方向相同一側的樁即承臺角點處的樁承受的豎直力最大,式(1)變為:
(2)
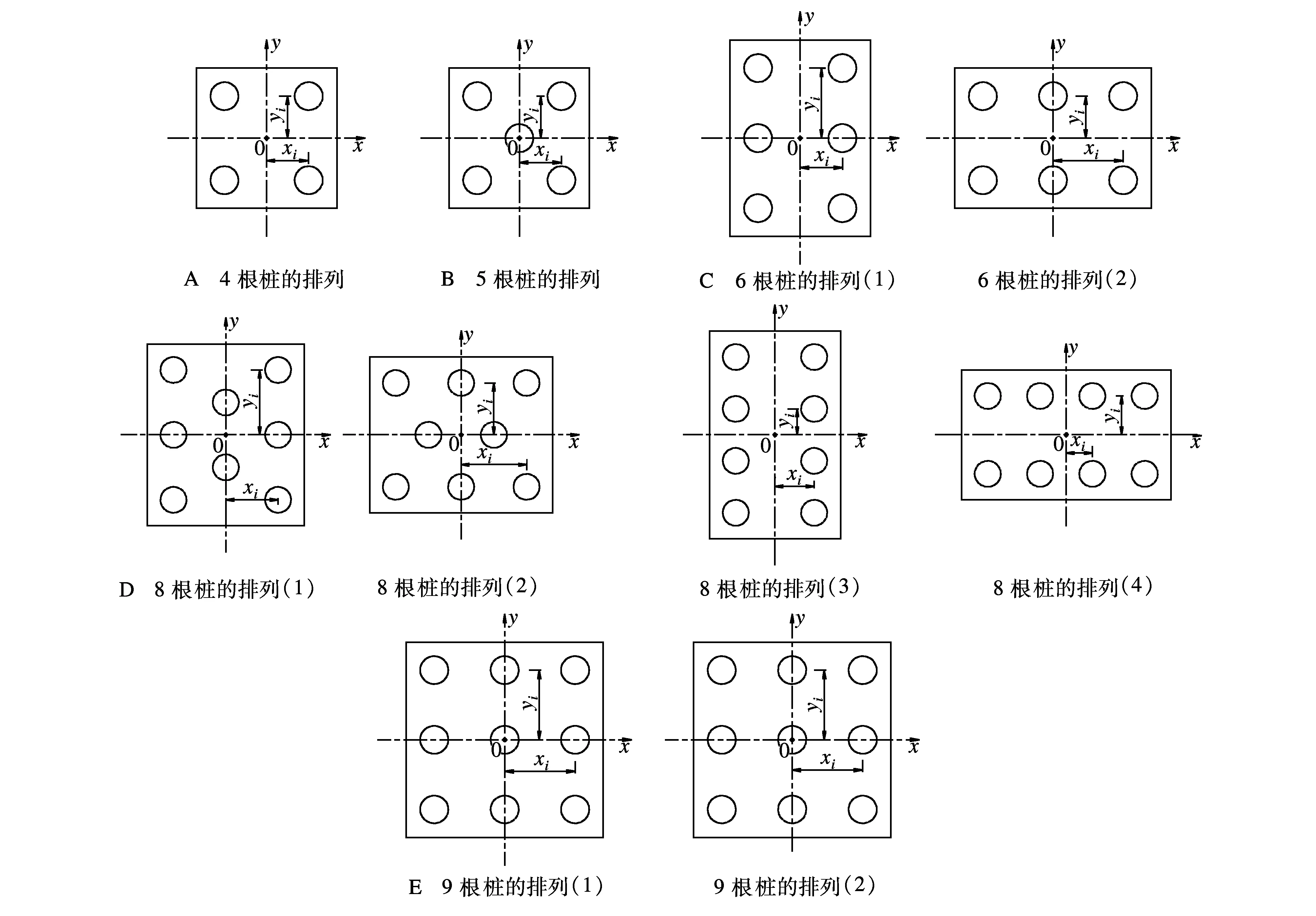
圖1 群樁的排列方式(圖中x軸表示縱橋向,y軸表示橫橋向)
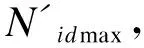
(3)
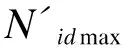
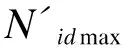
(4)
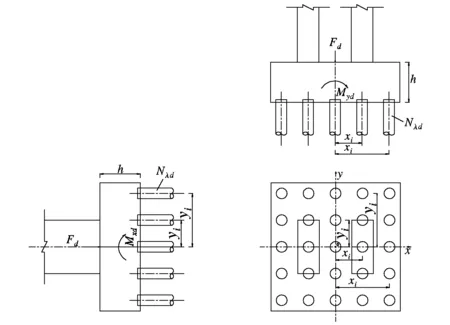
圖2 承臺樁基豎向力計算
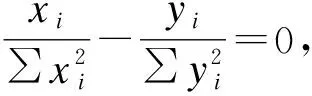
研究圖1中C的情況,將(1)旋轉90°且將x軸、y軸互換即得到圖(2)的情形,由此可知:

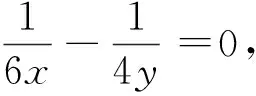
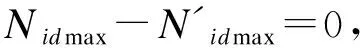
同理可推斷圖1中D(1)、(2)的情況:
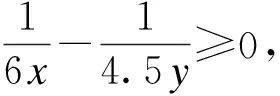
而圖1中D(3)、(4)的情況:
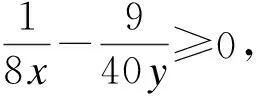
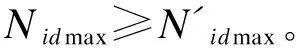
4 示 例
某連續剛構橋,布置為63m+110m+63m,橋寬為凈-6.5m+2×0.5m(防撞欄桿),設計荷載為公路—Ⅱ級,地震動峰值加速度系數為0.15。主墩為雙肢薄壁墩,高度均為25m,主墩基礎為14m×10m×4m的承臺加6根群樁基礎。其承臺加群樁基礎有兩種布置方式,具體布置見圖3。
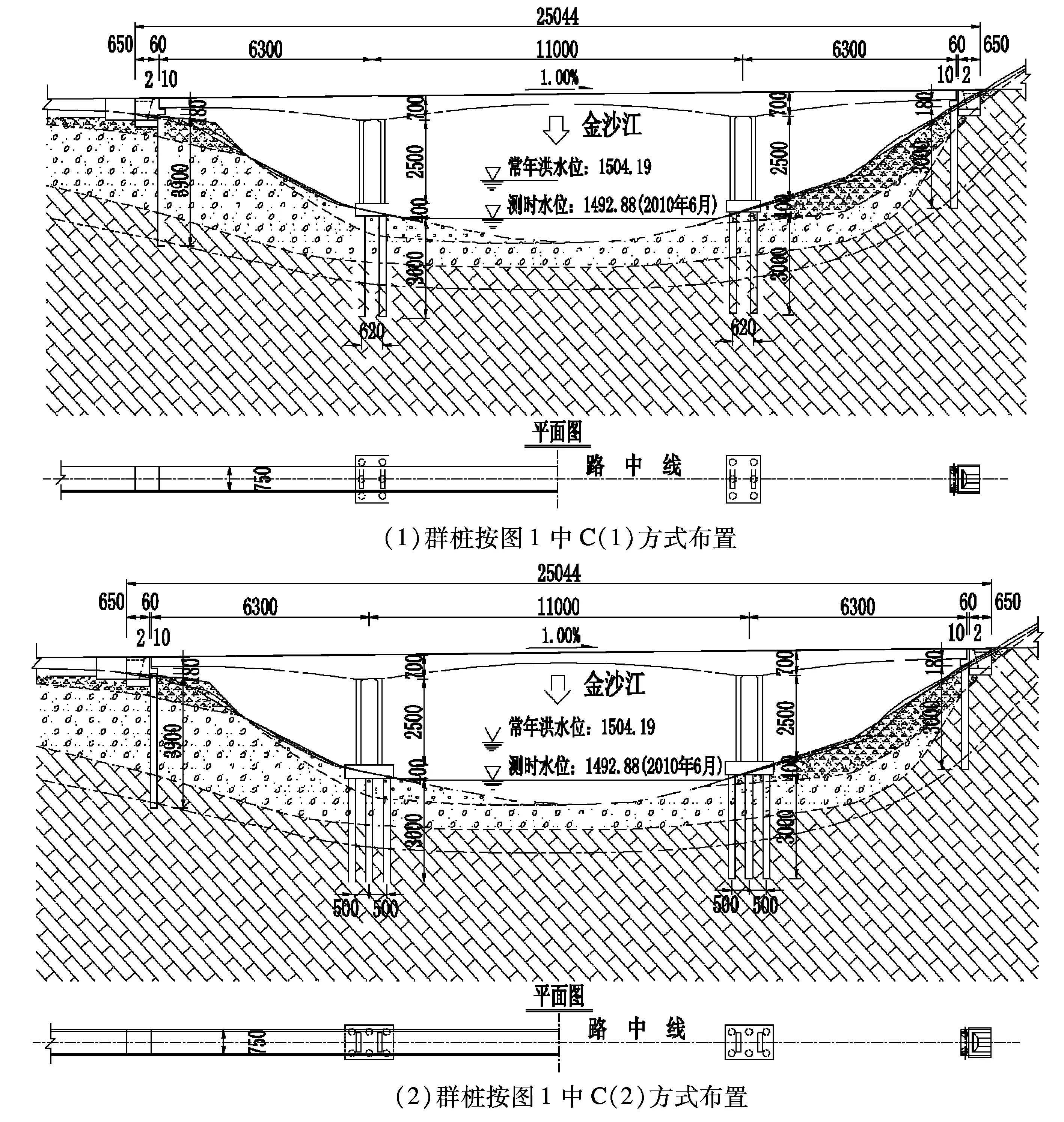
圖3 某連續剛構橋橋型布置
該橋在初步設計時,承臺及群樁基礎是按圖3中方式(1)布置的,該布置方式的優點是橋墩的每個墩肢縱向均對應3根樁基,橋墩傳力方式明確,但承臺在縱橋向似乎作用不大,僅起聯系墩身及樁基的作用。考慮到按圖3中方式(2)布置時,承臺能很好地發揮傳力作用,樁基受力更均勻,所以又按方式(2)進行了計算。
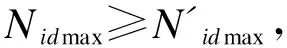
為了驗證以上結論的可靠性,針對以上橋型布置,采用橋梁結構計算專用程序MidasCivil建立兩個模型分別進行計算,得到在正常使用極限狀態下的組合結果(見表1)。
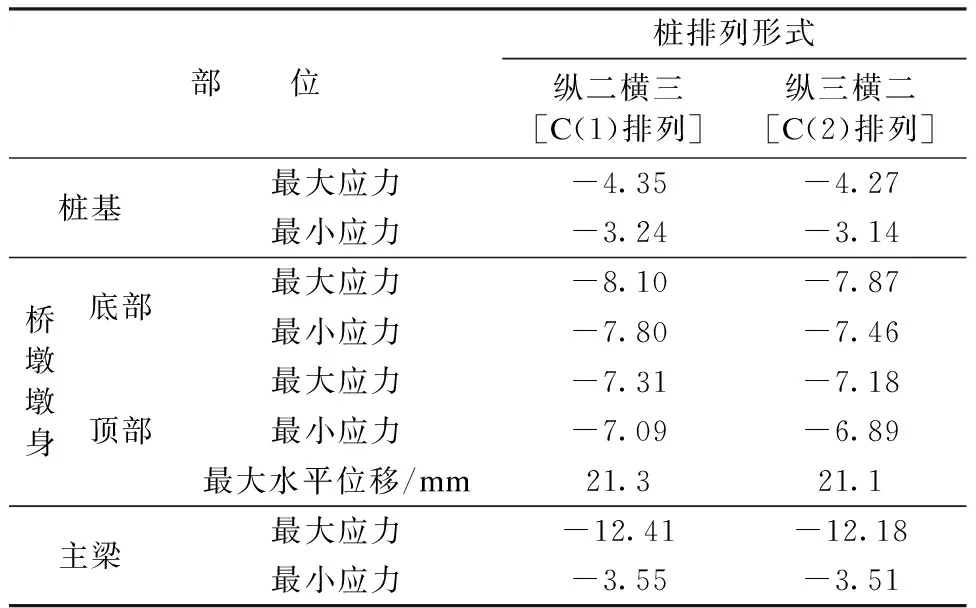
表1 正常使用極限狀態下組合結果 MPa
從表1可知,樁基按縱三橫二(即圖1C(2)中方式)進行排列時,各項計算值均比按縱二橫三(即圖1C(1)中方式)排列時的計算值略小,從而進一步驗證了縱三橫二的排列方式更合理。
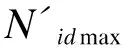
5 結 語
(1)群樁的排列方式對橋梁整體剛度有一定的影響。由于橋梁一般縱向受力較大,群樁布置時使其縱橋向剛度較大則更合理,即群樁的排列方式在一般情況下以縱橋向多排橫橋向少排受力相對更合理。
(2)在特殊情況下(如橫向力風力、地震力、撞擊力較大時),為了增加橋梁橫向剛度,也可將樁基按橫橋向多排縱橋向少排的方式排列,此時相比樁基縱橋向多排橫橋向少排的方式排列,對橋梁其它部位應力的影響并不明顯。
(3)當山區某些橋梁布置橋梁承臺時,若承臺縱橋向長度比橫橋向長度長,靠岸側可能引起更大的邊坡開挖,靠河側可能使承臺和樁基更伸入河床而增加施工難度時,也可以將承臺長邊布置在橫橋向,短邊布置在縱橋向,相應樁基也應適當調整。
參考文獻:
[1] 中交公路規劃設計院.JTG D62-2004《公路鋼筋混凝土及預應力混凝土橋涵設計規范》[S].北京:人民交通出版社,2004.
[2] 中交公路規劃設計有限公司.JTG D63-2007《公路橋涵地基與基礎設計規范》[S].北京:人民交通出版社,2007.
[3] 趙明華.橋梁樁基計算與檢測[M]. 北京:人民交通出版社,2000.

