不同擇優生長取向角枝晶生長的數值模擬

石玉峰，許慶彥，柳百成

(清華大學 機械工程系 先進成形制造教育部重點實驗室，北京 100084)

通過數值模擬手段來模擬枝晶形貌及微觀偏析，可以達到控制組織形態并且預測鑄件性能的目的。目前在微觀組織模擬方面主要的兩種方法是元胞自動機(Cellular automaton)和相場法(Phase field)。其中，CA方法通過耦合實際溫度場和溶質場，結合枝晶生長動力學理論以及隨機形核與長大物理機理，能夠描述晶粒度以及微觀枝晶形貌，同時能夠模擬確定鑄造條件下的等軸晶生長、定向凝固柱狀晶生長以及柱狀晶-等軸晶轉變等現象，因此，CA方法在最近的十幾年以來得到了較為廣泛的應用。很多學者對CA方法進行了不同的改進，出現了很多改進CA模型，已經可以用來模擬多種合金在不同鑄造工藝條件下枝晶形貌的演變[1-8]。對于立方晶系合金來說，〈100〉是枝晶的擇優生長取向，固液界面能在〈100〉方向上具有最低值，〈100〉方向上生長速率較高，故枝晶一次臂最容易沿著擇優生長取向進行生長。實際枝晶的擇優生長取向與坐標軸水平方向可能不平行，也即擇優生長取向角在0°～90°之間，但是CA模型在模擬立方晶系合金的枝晶生長過程中，由于正交元胞帶來的網格各向異性導致CA模型在描述任意擇優生長取向角的枝晶生長時會出現計算偏差，從而在最終枝晶一次臂生長過程中逐漸丟失自身固有的擇優生長取向，僅能沿著0°或 45°方向角生長。國內外許多學者通過對 CA捕獲算法進行改進以消除網格各向異性的影響，GANDIN和RAPPZ[9]首次提出了偏心立方捕獲算法，以最大限度消除網格各向異性對枝晶擇優生長取向的影響，來實現枝晶一次臂沿枝晶擇優生長取向的生長，但是偏心立方捕獲算法需要人為對枝晶尖端進行實時修正，算法較為復雜；DONG和LEE[10]在CA-FD模型中采用偏心立方捕獲算法[9]并耦合溶質場模擬了 Al-Cu合金定向凝固過程中的CET轉變，再現了擇優生長取向與坐標軸成多個不同夾角的枝晶生長形貌；LIU等[11]在CA模型中通過坐標旋轉法將枝晶擇優生長取向角旋轉到任意值，模擬了Al-4.5%Cu合金的單個等軸枝晶形貌；于靖等[12]在CA模型中采用一種“父子單元法”的捕獲算法，耦合溶質擴散方程計算了不同擇優生長取向角的單枝晶生長形態；ZHU和STEFANESCU[13]在CA模型中使用界面前沿追蹤方法來跟蹤枝晶生長過程中的固液界面推移，模擬了Al-Cu合金多個不同擇優生長取向角的枝晶形貌演化。

本文作者在已有CA模型的基礎上，在計算界面生長速率方程時考慮了擇優生長取向的長程作用，并對界面生長速率方程采用斜中心差分格式進行離散，從而建立了可模擬多個不同擇優生長取向角的枝晶生長的MCA模型。選取NH4Cl-H2O系透明合金模擬了單個等軸枝晶和多個不同擇優生長取向角的枝晶生長，模擬結果與實驗結果符合較好；同時模擬了NH4Cl-H2O系透明合金的擇優生長取向與坐標軸不平行時的柱狀枝晶生長過程，并進行了實驗驗證。

1 數學模型和數值算法

1.1 模型假設

1)在本研究微觀組織模擬MCA模型中，假設微觀區域與外界無溶質交換，計算域中溶質質量守恒；

2) 凝固過程中的凝固速率較小，其溶質Péclet數小于 1，故可假設凝固過程中固液界面處于局部熱力學平衡狀態；同時由于動力學過冷一般很小，故本模型忽略動力學過冷；

3) 由于液相中溶質擴散系數比固相中的大幾個數量級，因此忽略固相溶質擴散，凝固過程中僅考慮液相溶質擴散。

4) 二維計算域被劃分成M×N個正方形元胞，元胞尺寸Δx=Δy；元胞狀態的標識為元胞的固相分數fS：液態(fS=0)、固態(fS=1)和界面狀態(0＜fS＜1)。

1.2 溶質傳輸控制方程

二元合金枝晶生長過程中，其液相和固相溶質傳輸方程形式分別為

式中：CL和DL分別是液相溶質成分和液相溶質擴散系數；k0為溶質平衡分配系數；fS是固相分數。式(1)右端第二項表示界面元胞由于固相分數的增加所導致的界面溶質再分配。

式中：CS和DS分別是固相溶質成分和固相溶質擴散系數。固液界面上的溶質再分配滿足如下方程

1.3 界面熱力學平衡

在二元合金枝晶生長過程中，由于界面元胞滿足局部熱力學平衡條件，因此界面元胞的平衡溫度滿足

式中：T為界面平衡溫度，也即界面元胞的實際溫度場；TL是初始溶質成分C0所對應的液相線溫度；ΔTR和ΔTC分別表示曲率過冷和成分過冷。

1) 曲率過冷

在二維條件下，考慮Gibbs-Thomson效應的二元合金凝固界面曲率過冷表達式為[14]

式中：Г是Gibbs-Thomson系數；f(ψ)是立方晶系界面能各向異性函數；ψ是固液界面元胞單位法向矢量n所對應的平面角；K是界面曲率。其中二維條件下f(ψ)計算公式為

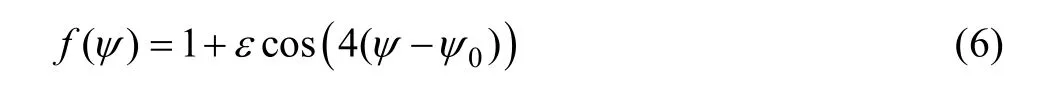
式中：ε為界面能各向異性系數；ψ0是枝晶的擇優生長取向角；通過式(5)～(6)可以得到界面曲率過冷計算公式為

單位法向矢量n與界面元胞的固相分數fS有關，其表達式為

式中：nx和ny為法向矢量n在x和y方向的分量。

CA界面元胞曲率K受到元胞自身以及周圍元胞的固相分數控制，二維條件下界面元胞曲率的計算方法見參考文獻[15]。

2) 成分過冷

對于二元合金枝晶生長過程，由于界面前沿液相溶質擴散系數是有限值，因此在界面前沿溶質再分配造成的溶質富集形成了界面元胞的成分過冷，其表達式如下

式中：mL是液相線斜率；CL*是界面平衡溶質成分。在二元合金CA模型中假設液相線斜率為常數，不隨溫度和溶質成分變化。

3) 界面平衡溶質成分

通過聯立式(5)和(10)同時根據式(3)可以得到界面平衡液相溶質成分CL*和固相溶質成分CS*的計算公式為

1.4 界面元胞固相分數增量

1) 界面位置矢量與擇優生長取向之間的夾角β

枝晶生長過程中的擇優生長取向與坐標軸x不一定重合，即 0°≤ψ0＜90°。在CA 枝晶生長模擬過程中，界面元胞的生長僅受到周圍最近鄰或者次近鄰的4個元胞的影響，故隨著枝晶生長，會逐漸丟失自身擇優生長取向而趨向于沿著坐標軸或與坐標軸成 45°方向生長。為了消除這種網格各向異性帶來的副作用，需要考慮界面元胞位置矢量與擇優生長取向間的夾角β，β越接近0°或者90°，則表明界面元胞越接近擇優生長取向，其生長越快。由此，當界面元胞與形核核心的位置越來越遠時，可以避免枝晶逐漸丟失其自身固有的擇優生長取向。圖1所示為擇優生長取向與界面元胞位置矢量夾角示意圖。擇優生長取向px=(cosψ0, sinψ0)，py=(-sinψ0, cosψ0)；計算域中枝晶形核核心為O(i0,j0)，界面元胞位置坐標為(i,j)，定義界面元胞與x軸方向夾角為α，其單位方向矢量p0=(cosα,sinα)，計算方法如下

式中：i0和j0為形核核心O的x和y方向坐標值，i和y是界面元胞P的坐標值。

圖1 擇優生長取向與界面元胞位置矢量夾角示意圖Fig.1 Schematic illustration of intersection angle between preferred growth orientation and interface cell position vector

在計算任意位置界面元胞固相分數增加量的過程中，首先計算界面元胞位置矢量p0與擇優生長取向px的夾角β，其計算公式如下：

2) 界面生長速率

二元合金枝晶固液界面上存在溶質質量守恒，為了消除網格各向異性對界面元胞法向生長速率的影響，需要考慮擇優生長取向的作用，故界面元胞法向生長速度w的表達式為

式中：ψ是界面元胞的法向矢量和x軸的夾角。

3) 界面元胞固相分數增量計算

界面元胞固相分數增量 ΔfS與固液界面法向生長速率w之間的關系式如下[2]

式中：L是考慮擇優生長取向作用下的界面元胞空間步長；Δt是時間步長；fSn和fSn+1分別表示當前時刻和下一時刻界面元胞的固相分數。當界面元胞固相分數fS達到1時，開始對周圍液相元胞進行捕獲，具體捕獲規則見參考文獻[12]。

1.5 數值求解方法

在MCA模型求解過程中，對界面生長速率方程(16)中的一階導數項采用斜中心差分格式進行離散，如圖2所示為考慮擇優生長取向角ψ0后的斜中心差分格式示意圖，其中d是元胞P的空間步長，其大小與Δx相等。

圖2 斜中心差分格式示意圖Fig.2 Schematic diagrams of central difference scheme:(a) 0°≤ψ0≤45°; (b) 45°＜ψ0＜90°

根據圖2，可得到方程(16)中一階導數項的差分離散形式為式中：CL*是元胞P的界面平衡液相溶質成分；CL和CS是液相和固相溶質成分；N、S、W、E分別為元胞P上、下、左、右4個方向的鄰居元胞；d0是斜中心差分格式下的元胞步長，當0°≤ψ0≤45°時，d0=dsecψ0；當45°＜ψ0＜90°時，d0=dcscψ0。

當0°≤ψ0≤45°時，斜中心差分格式的E、W、N、S 4個元胞的液相溶質成分和固相分數的計算公式如下

對于斜中心差分格式的E、W、N、S 4個元胞的固相溶質成分計算方法同式(20)。

當45°＜ψ0＜90°時，斜中心差分格式的 E、W、N、S 4個元胞的液相溶質成分和固相分數的計算方法與式(20)和(21)有所不同，離散形式為

對于斜中心差分格式的E、W、N、S 4個元胞的固相溶質成分計算方法同式(22)。

MCA模型的求解流程如下所示：

1) 計算域劃分成M×N個正方形元胞，元胞狀態包含元胞大小、初始溶質成分和初始溫度；在計算域中形成若干具有一定擇優生長取向角ψ0的固相晶核，晶核捕獲周圍的液相鄰居元胞，使之成為界面元胞；

2) 確定計算域時間步長，Δt=Δx2/(5DL)；

3) 假設微觀計算域初始溫度均勻，其值為T0，且計算域以一定的冷卻速率CR下降，可以計算元胞任意時刻的界面平衡溫度T*。根據式(4)～(12)計算得到界面平衡液相溶質成分CL*和固相溶質成分CS*，其中方程(9)的一階導數項差分格式為

離散后的E、W、N、S 4個元胞的固相分數計算方法見式(21)和(23)。

4) 通過斜中心差分格式求解方程(16)，得到界面法向生長速率w；

5) 通過方程(17)計算界面元胞固相分數增量ΔfS；

6) 求解方程(1)～(3)，獲得液相、界面和固相元胞中的溶質成分分布；

7) 判斷界面元胞固相分數fS，若fS小于1，則重復步驟(3)～(6)；若fS等于 1，則轉變成固相元胞，并對周圍液相元胞進行捕獲。

2 模擬結果與實驗結果

2.1 氯化銨水溶液單個等軸晶生長過程模擬

實際合金凝固過程的直接實時觀察較為困難且實驗成本很高，而可在低溫下凝固的透明合金具有和實際合金類似的凝固潛熱、枝晶形貌特性和動力學行為，可代替實際合金來研究枝晶生長形貌演化機理。為了驗證本研究的MCA模型，選取NH4Cl-70%H2O(質量分數)溶液進行枝晶生長實驗。實驗過程中的冷卻速率為2.0 K/s，當溫度低于液相線溫度TL以下1 K時，在顯微鏡視野中產生晶核并開始長大。

模擬采用與實驗相同的冷卻速率，在選定的計算域中心形核，CA 元胞步長為 3 μm，計算域大小為1 500 μm×1 500 μm，枝晶擇優生長取向角ψ0為 0°。其余參數見表1。

如圖3(a)～(c)所示為模擬的NH4Cl-70%H2O透明合金單個等軸晶的形貌演化過程，圖3(d)所示為光學顯微鏡照片。從模擬結果可以看到，等軸晶形貌具有四重對稱性特征，符合立方晶系枝晶形貌特征，4個一次枝晶臂之間夾角互為 90°，且枝晶的擇優生長取向與x軸夾角為0°，即枝晶沿著初始確定的擇優生長取向生長。在凝固過程中，由于枝晶間溶質富集隨著過冷度增大而增加，導致一次枝晶臂上逐漸長出二次枝晶臂，與一次枝晶臂之間的夾角保持 90°。模擬得到的二次枝晶臂間距為51 μm，實驗得到的二次枝晶臂間距為 44.5 μm，模擬結果與實驗結果基本一致，從而說明MCA模型是可靠的。

表1 NH4Cl-70%H2O溶液的熱物性參數[16-18]Table1 Thermal physical properties of NH4Cl-70%H2O solution[16-18]

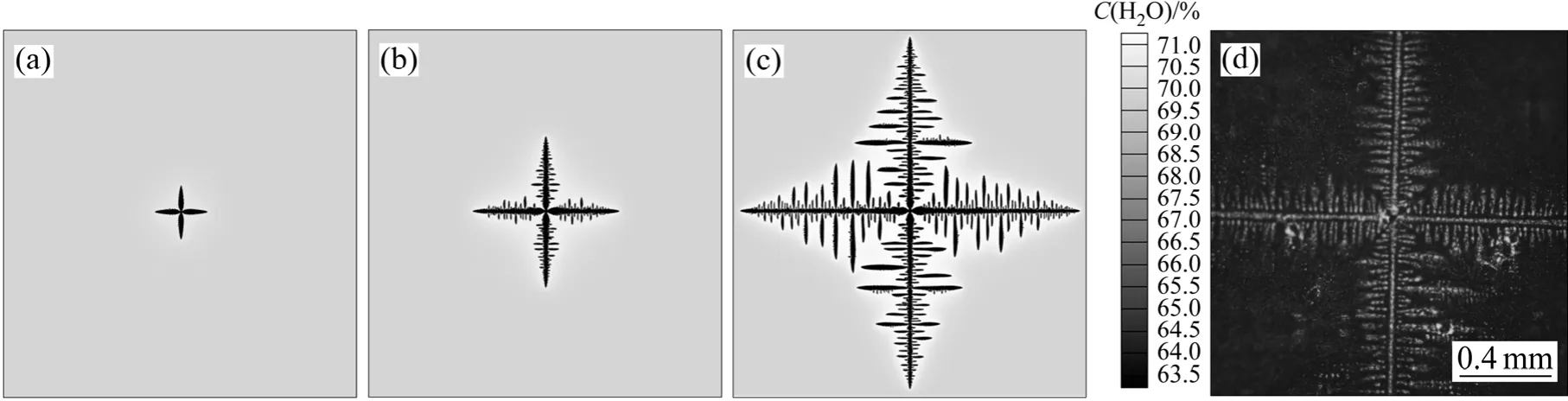
圖3 NH4Cl-70%H2O透明合金單枝晶生長模擬結果和實驗結果Fig.3 Simulated dendrite growth and experimental results of NH4Cl-70%H2O transparent alloy: (a) fS =0.5%; (b) fS=2.5%;(c) fS=9.0%; (d) Experimental result

2.2 不同擇優生長取向角枝晶生長模擬及實驗結果

采用本研究的MCA模型，在計算界面元胞生長過程中考慮枝晶擇優生長取向的作用，可以最大限度地消除網格各向異性的影響，實現立方晶系合金枝晶生長過程中保證自身的擇優生長取向不變。本節針對NH4Cl-74%H2O透明合金，進行枝晶生長過程的數值模擬，凝固過程的熱物性參數見文獻[15]。選取計算域大小為1.8 mm×2.4 mm，CA 元胞尺寸為5 μm，計算域冷卻速率CR為2 K/s，當溫度降低到液相線溫度TL以下5 K時，計算區域形核。

圖4(a)～(c)所示為模擬具有不同擇優生長取向角的枝晶形貌演化，其擇優生長取向角ψ0分別為50°、0°、75°和60°(自左至右)。如圖4(a)所示，生長初期二次枝晶臂并不發達，隨著生長的繼續，枝晶界面前沿和枝晶間溶質逐漸富集，如圖4(b)和4(c)所示，導致各處成分過冷出現差別，從而二次枝晶臂逐漸出現。從圖4(a)～(c)可以看出，各個枝晶在生長過程中自身的擇優生長取向并沒有因網格各向異性的影響而改變，一次枝晶臂始終沿著擇優生長取向生長。如圖4(d)所示為實驗獲得的NH4Cl-74%H2O透明合金枝晶結果，經過測量可得到實驗獲得的四枝晶的擇優生長取向角ψ0分別為 48°、0°、78°和63°，兩者吻合較好。模擬過程中4個枝晶的一次枝晶臂上出現的二次枝晶臂與一次臂主干的夾角均保持 90°，符合 NH4Cl-74%H2O透明合金枝晶特征，與實驗結果一致，說明本研究的MCA模型可用來模擬不同擇優生長取向角的多個枝晶的生長形貌演化。

2.3 定向凝固柱狀晶生長過程數值模擬與實驗驗證

本節對NH4Cl-74%H2O透明合金柱狀枝晶定向凝固過程進行模擬，凝固過程中選取與實驗過程一致的溫度梯度G=1 K/mm，方向沿著豎直方向。模擬采用CA元胞數量為720×480，元胞尺寸為5 μm，熱物性參數取值見文獻[15]。當計算域溫度降低到液相線溫度TL以下5 K時，計算域底部形核，共產生9個形核核心，具有相同的擇優生長取向角ψ0=60°。在抽拉速度vp=8 μm/s的作用下，柱狀枝晶開始生長。

圖5所示為模擬得到的NH4Cl-74%H2O透明合金定向凝固柱狀枝晶溶質場分布的模擬結果和實驗結果。其中柱狀枝晶的擇優生長取向角ψ0為60°，在溫度梯度G和抽拉速度vp的作用下，枝晶界面前沿過冷度不斷增大；如圖5(a)和5(c)所示，枝晶間和枝晶界面前沿隨著過冷度的增大出現了溶質富集，由于成分過冷和曲率過冷的作用，柱狀枝晶一次枝晶臂上出現二次枝晶臂甚至三次枝晶臂，且三次枝晶臂與二次枝晶臂之間以及二次枝晶臂與一次枝晶臂之間的夾角均保持 90°，符合立方晶系合金特征。柱狀枝晶在生長過程中，一次枝晶臂沿著擇優生長取向方向生長速度最快，圖5(b)和5(d)的實驗結果證明了定向凝固過程中柱狀枝晶一次枝晶臂始終沿著擇優生長取向的方向生長，與水平方向夾角保持 60°，與模擬結果吻合較好。同時，實驗過程中測量的平均一次枝晶臂間距為32 μm，與模擬得到的平均一次枝晶臂間距36 μm相差較小，說明MCA模型可以預測定向凝固過程中擇優生長取向與坐標軸不平行時的柱狀枝晶的形貌演化。

圖4 NH4Cl-74%H2O透明合金不同擇優生長取向角的多個枝晶生長的模擬結果和實驗結果Fig.4 Simulated and experimental results of multiple dendrite growth of NH4Cl-74%H2O transparent alloy with random preferred growth orientation angles: (a) t=1.2 s, fS=1.5%; (b) t=2.4 s, fS=5.5%; (c) t=3.4 s, fS=12.0%; (d) OM photograph

圖5 NH4Cl-74%H2O透明合金定向凝固柱狀枝晶形貌的模擬和實驗結果Fig.5 Simulated and experimental columnar dendrite morphologies of NH4Cl-74%H2O transparent alloy directionally solidified with constant preferred growth orientation angles: (a) Simulated result, t=200 s, G=1 K/mm, vp=8 μm/s; (b) Experimental result;(c) Simulated result, t=270 s, G=1 K/mm, vp=8 μm/s; (d) Experimental result

3 結論

1) 考慮枝晶擇優生長取向角的隨機性對枝晶界面法向生長速率的影響，建立了MCA模型以模擬不同擇優生長取向角的枝晶形貌演化。

2) 使用MCA模型對NH4Cl-70%H2O溶液單個等軸枝晶的生長過程進行模擬，枝晶的擇優生長取向與坐標軸平行，模擬結果很好地再現了一次枝晶臂的生長以及二次枝晶臂的產生與發展。同時，模擬和實驗得到的二次枝晶臂間距吻合較好，枝晶形貌也基本一致。

3) 選擇 NH4Cl-74%H2O溶液進行多個等軸枝晶自由生長的實驗與模擬。模擬得到的不同擇優生長取向的等軸枝晶形貌與實驗結果吻合較好，說明 MCA模型可以模擬不同擇優生長取向角的立方晶系合金的枝晶生長過程。

4) 采用MCA模型對NH4Cl-74%H2O溶液定向凝固柱狀枝晶形貌演化進行了模擬，模擬結果與實驗結果基本一致，說明MCA模型可以模擬一定擇優生長取向角的柱狀枝晶的形貌演化。

[1]NASTAC L.Numerical modeling of solidification morphologies and segregation patterns in cast dendritic alloys[J].Acta Materialia, 1999, 47: 4253-4262.

[2]BELTRAN-SANCHEZ L, STEFANESCU D M.A quantitative dendrite growth model and analysis of stability concepts[J].Metall Mater Trans A, 2004, 35: 2471-2485.

[3]WANG W, LEE P D, MCLEAN M.A model of solidification microstructures in nickel-based superalloys: Predicting primary dendrite spacing selection[J].Acta Materialia, 2003, 51:2971-2987.

[4]LIU B C, XU Q Y, JING T, SHEN H F, HAN Z Q.Advances in multi-scale modeling of solidification and casting processes[J].JOM, 2011, 63(4): 19-25.

[5]LIU X B, XU Q Y, JING T, LIU B.Microstructure of aluminum twin-roll casting based on cellular automaton[J].Transactions of Nonferrous Metals Society of China, 2008, 18(4): 944-948.

[6]ZHU M F, HONG C P, STEFANESCU D M, CHANG Y A.Computational modeling of microstructure evolution in solidification of aluminum alloys[J].Metall Mater Trans B, 2007,38: 517-524.

[7]LIU B C, XIONG S M, XU Q Y.Study on macro- and micromodeling of the solidi fi cation process of aluminum shape casting[J].Metall Mater Trans B, 2007, 38: 525-532.

[8]李 強, 李殿中, 錢百年.應用連續性方法模擬枝晶生長[J].金屬學報, 2004, 40(6): 634-638.LI Qiang, LI Dian-zhong, QIAN Bai-nian.Modelling of the dendrite growth by using continuous method[J].Acta Metall Sin,2004, 40(6): 634-638.

[9]GANDIN C A, RAPPAZ M.A 3D cellular automaton algorithm for the prediction of dendritic grain growth[J].Acta Materialia,1997, 45: 2187-2195.

[10]DONG H B, LEE P D.Simulation of the columnar-to-equiaxed transition in directionally solidi fi ed Al-Cu alloys[J].Acta Materialia, 2005, 53: 659-668.

[11]LIU Y, XU Q Y, LIU B C.A modified cellular automaton method for the modeling of the dendritic morphology of binary alloys[J].Tsinghua Science and Technology, 2006, 11(5): 495-500.

[12]于 靖, 許慶彥, 崔 鍇, 柳百成.基于一種改進 CA模型的微觀組織模擬[J].金屬學報，2007, 43(7): 731-738.YU Jing, XU Qing-yan, CUI Kai, LIU Bai-cheng.Numerical simulation of microstructure evolution based on a modified CA method[J].Acta Metall Sin, 2007, 43(7): 731-738.

[13]ZHU M F, STEFANESCU D M.Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys[J].Acta Materialia, 2007, 55: 1741-1755.

[14]MICHELIC S C, THUSWALDNER J M, BERNHARD C.Polydimensional modelling of dendritic growth and microsegregation in multicomponent alloys[J].Acta Materialia,2010, 58: 2738-2751.

[15]石玉峰, 許慶彥, 龔 銘, 柳百成.定向凝固過程中NH4Cl-H2O枝晶生長的數值模擬[J].金屬學報, 2011, 47(5):620-627.SHI Yu-feng, XU Qing-yan, GONG Ming, LIU Bai-cheng.Simulation of NH4Cl-H2O dendritic growth in directional solidification[J].Acta Metall Sin, 2011, 47(5): 620-627.

[16]HANSEN G, LIU S, LU S Z, HELLAWELL A.Dendritic array growth in the systems NH4Cl-H2O and [CH2CN]2-H2O: Steady state measurements and analysis[J].Journal of Crystal Growth,2002, 234: 731-739.

[17]BENNON W D, INCROPERA F P.The evolution of macrosegregation in statically cast binary ingots[J].Metall Mater Trans B, 1987, 18: 611-616.

[18]馮妍會, 聶 紅, 張欣欣.定向凝固宏微觀熱質傳遞及雙擴散流作用[J].工程熱物理學報, 2008, 29(2): 301-305.FENG Yan-hui, NIE Hong, ZHANG Xin-xin.Coupled macro-micro transports with double diffusive flow during directional solidification[J].Journal of Engineering Thermophysics,2008, 29(2): 301-305.