材料三維彈塑性應力應變關系分析及Neuber準則適用性驗證

□胡天翼（西安交通大學）

1.前言

含圓孔平板在自身受力時出現的應力集中問題是工程中普遍存在的問題，其平面模型是彈性力學中的經典模型，已有了精確的解析解。與平面問題相比，考慮了厚度效應和三維尺寸效應的三維分析更加符合工程實際，因此也更具有指導意義。然而由于三維材料的復雜性和彈塑性狀態應力-應變分布的特殊性，目前對帶孔圓板的研究主要集中于對構件進行彈性分析，或假定平板厚度足夠小，使各項參數能夠在厚度方向均勻分布，而對三維彈塑性材料應力-應變關系的準確推導尚無完全定論。用于預測材料局部彈塑性應力應變場的Neuber準則已經在二維彈塑性分析中得到了廣泛應用，但其在三維分析領域的準確性依然值得商榷。

文章以胡克定律為立足點，對三維彈塑性材料的應力-應變關系做了進一步的推導，并通過三維有限元方法建立了單軸拉伸狀態下的含圓孔有限厚度板模型進行應力應變分析，將其結果與所推導的應力-應變關系對比驗證。本文還討論了Neuber準則對三維構件的適用性，并對其在三維條件下的保守程度與二維條件做了對比。

2.Neuber平衡方程簡介和有限元模型介紹

2.1 Neuber平衡方程簡介

在分析圓孔根部彈塑性應力應變時，由Neuber提出了平衡方程：

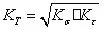
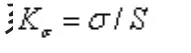
2.2 有限元分析模型

模型計算借助大型有限元計算軟件ANSYS-10.0完成。選取1/8試樣，坐標原點位于板厚中面圓心，在試樣長度、寬度、厚度中面加載對稱約束，圓孔遠端沿y方向加載大小為N的均勻拉應力。圓孔的半徑圖1模型的網格劃分為r，板的長度2L=400mm，寬度2W=200mm(當r/W<5時，可近似認為圓孔很小，試樣為無限大)，厚度為2B=30mm，如圖1所示：

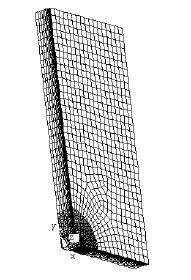
圖1 模型的網格劃分圖

在分析中，采用8節點三維實體單元，沿試樣的1/2厚度處取15層單元，每層單的厚度從板的厚度中面到表面逐漸減小，間距比率取0.1。在每一單元層的圓孔周圍畫出三倍半徑大小的細化區，采用映射劃分(應力集中和塑性區主要出現在三倍半徑范圍以內)，三倍半徑以外區域單元尺寸較大(經實測將二維平板照此方式劃分網格，計算結果能很好地符合解析解，誤差在1%以內)。在板遠端作用有的均勻分布拉應力，材料的彈性模量和泊松比分別為200GPa和0.3，屈服強度300Mpa，切線模量為0，本構關系見圖2。

圖2 材料本構的定義圖

3.三維彈塑性狀態下應力應變關系的推導

其中：

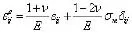
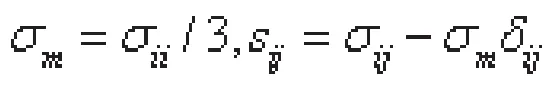
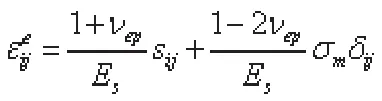
將上式代入離面約束Tz及面內約束Tx表達式：

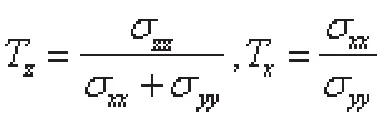
則有應力應變關系表達：

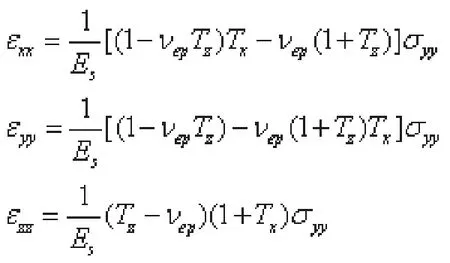
將割線模量Es用等效應變表達，同時表示出彈塑性泊松比νep：

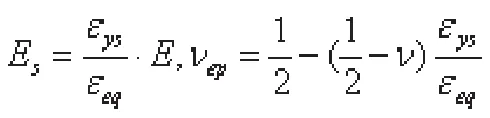
即可得到以Tz，Tx和εep表示的各方向應變：

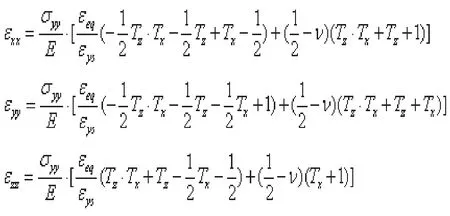
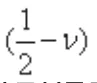
這里，我們仍然使用前述的Ansys模型提取數據進行計算，來對上述公式進行驗證驗證。

取2.2中所介紹之模型，令N=230MPa，在塑性區內取出5個具有代表性的點，分別提出 σyy，εep，Tz，Tx這幾個值，并計算出，，與實際應變作為對比。

根據表1可以看出，由該式計算出的應變值基本滿足精度要求，較為準確。

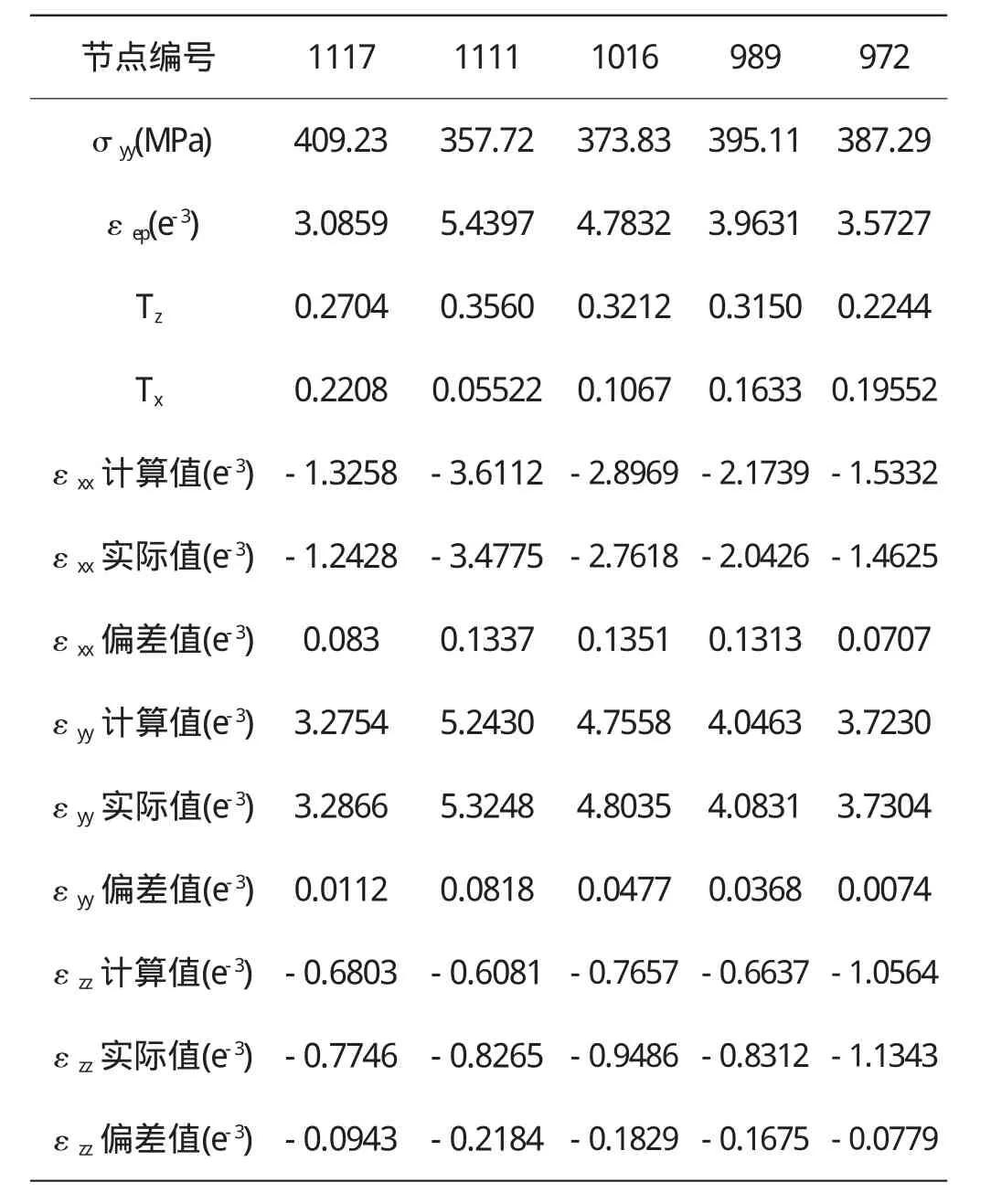
表1 應力-應變關系公式計算結果與實際應變值對比表

4.三維狀態下Neuber準則適用性的討論

在工程斷裂力學領域，對于一個含缺口的受力試樣而言，Neuber準則是最為常用的反映缺口根部應力-應變集中與理論應力集中關系的準則之一。Neuber準則的平衡方程已在本文第二部分提到，其在二維彈塑性領域的適用性也已得到廣泛認可。然而Neuber準則在用于估計局部應力應變場時往往給出過高的預測結果，也即是預測結果偏保守[6]，那么將Neuber準則應用于三維領域會產生和二維分析相同的效果嗎，其結果是否也會偏保守，保守的程度如何？本部分將依然使用前述的Ansys模型提取數據進行計算，來驗證Neuber準則在三維狀態下的適用性。

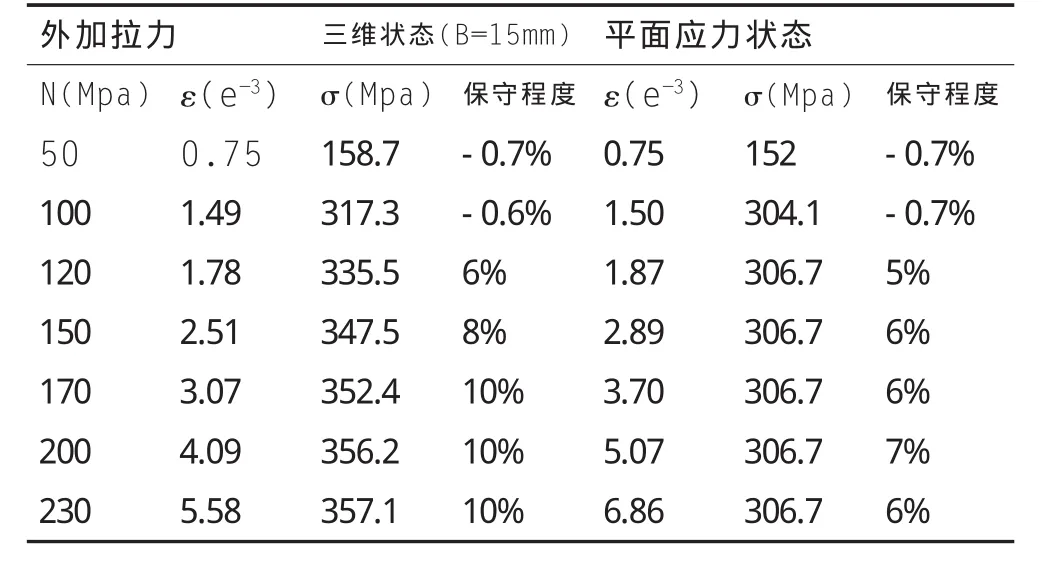
表2 不同拉力下三維和二維狀態Neuber準則的保守程度對比表

表2為2.2中所介紹之三維模型與其他條件均相同的平面板，由Neuber準則計算所得結果的保守程度對比。表中和分別為由Ansys計算所得的試樣局部應變和局部應力。

由該表可以看出，在材料進入彈塑性以后 (拉力N>100Mpa)，Neuber準則的估計值比真實值要保守，保守的程度都在5%-10%之間。相比二維狀態，三維用Neuber準則估計出的結果比二維狀態普遍更為保守，也即是說，用Neuber準則來估計三維試樣的局部應力應變同樣是安全的。

5.結論

一是板中任意一點的各向應變值均可由σyy，εep，Tz，Tx表示出，應變值ε與這些值均呈正比關系；二是Neuber準則在三維彈塑性試樣估計中仍然具有適用性，并且在三維分析中用Neuber準則估算出的結果比二維狀態更為保守，所以此時Neuber準則依然是安全的。