雙軸旋轉慣導系統轉位誤差對導航精度影響研究

吳修振，周紹磊，李瑞濤

(海軍航空工程學院控制工程系，山東煙臺264001)

0 引言

理想情況下，如果系統的慣性元件只存在漂移誤差，根據捷聯慣導的原理［1］，旋轉式慣導系統(INS)的轉位運動不會引起任何的附加誤差。然而，實際上慣性元件的標度因數誤差和安裝誤差總是存在，它們可能與轉位運動耦合而在系統中引起以外的誤差效應。研究表明:理想條件下，恰當的雙軸轉位方案可以補償掉慣性元件的漂移誤差、安裝誤差以及非對稱標度因數誤差。然而，當轉位運動存在誤差時，雙軸旋轉INS的誤差補償效果會發生改變，本文通過研究非對稱標度因數誤差對導航精度的影響機理，仿真分析了轉位運動誤差與陀螺非對稱標度因數誤差的耦合誤差效應，得出了一些具有實際借鑒意義的結論。

1 陀螺非線性標度因數誤差效應分析

1.1 非線性標度因數誤差引起的數學平臺誤差角度

慣性元件的標度因數不可能標定得絕對準確，而且標度因數還可能隨著時間、環境等因素而改變，造成了實際系統中總存在著慣性元件的標度因數誤差。另外，由于原理、工藝等原因，一般標度因數還存在著正反不對稱性，會引起一定的標度因數不對稱誤差［2］。為簡化分析，在單軸旋轉的條件下分析陀螺非線性標度因數誤差效應，結果可以推廣到雙軸旋轉。

考慮到正反標度因數的不對稱性，設3只正交安裝的陀螺分別感受到的輸入角速度為ω1，ω2，ω3，令

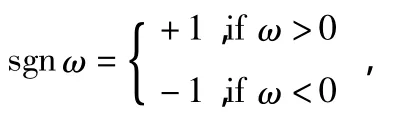
則IMU中3個陀螺的非對稱標度因數誤差矩陣Sg可表示為

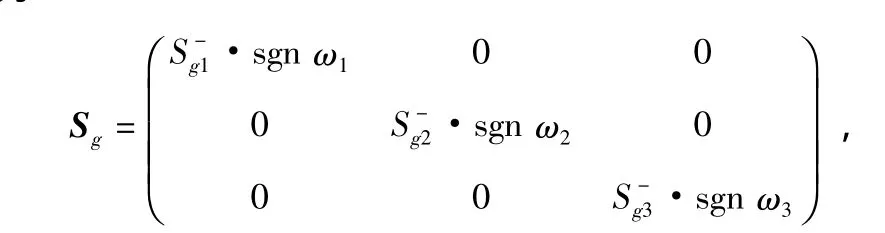
式中 S-gi為第i(i=1，2，3)個陀螺的非對稱標度因數誤差，亦即為正向標度因數和反向標度因數之差的一半。

導航坐標系采用東北天地理坐標系，并且初始時刻姿態矩陣為單位矩陣，初始時刻的東北天方位和3只陀螺的敏感軸重合，從0時刻開始，控制系統的IMU繞豎直方向以角速度ω開始勻速轉動，則可得t時刻的姿態矩陣為

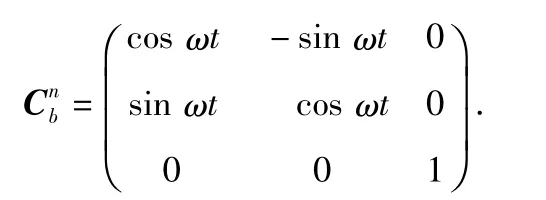
3只陀螺的輸入角速度為

其中，ωieN和ωieU分別為地球自轉在北向和天向上的分量。

由式(1)，t時刻當3只陀螺輸入角速度分別為ω1，ω2，ω3時，IMU機體系中由陀螺的非線性標度因數誤差所產生的角速度誤差為

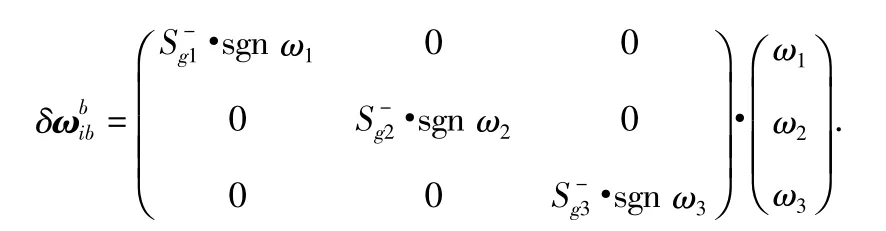
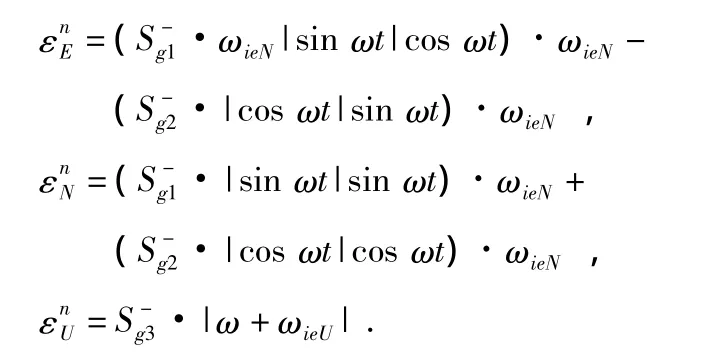
將上面數學平臺的角速度誤差項在時間T=2π/|ω|內積分，則得到轉動一周后數學平臺的累積誤差角度

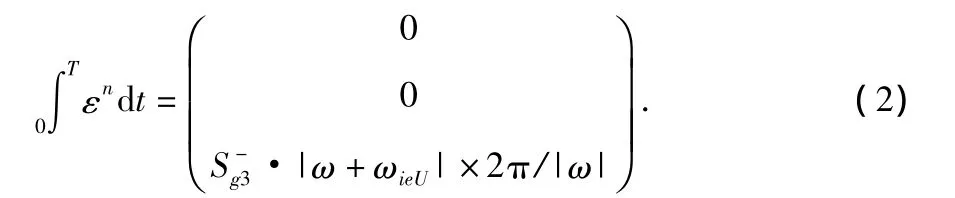
1.2 非對稱性標度因數誤差的自動補償效應

根據式(2)的前2個分量可以發現，在旋轉運動的一個周期內，與轉軸垂直方向上的2只陀螺的標度因數的非對稱性誤差項S-g1，S-g2消失了，即單軸轉動可以平均掉敏感軸與轉軸垂直的陀螺的非對稱性標度因數誤差所引起的導航誤差。

將以上結論推廣，對于雙軸旋轉INS，在隔離載體運動的情況下，可以“平均掉”所有慣性元件的非對稱性誤差效應。上面是在理想境況下得到的結論，如果系統的轉軸受控制精度和碼盤精度的影響，轉動時存在誤差，轉位誤差會和非對稱標度因數誤差發生耦合作用，最終將可能導致導航誤差的積累甚至發散。

2 轉位誤差與非對稱標度因數誤差耦合效應分析

對于雙軸旋轉INS，目前合理的轉位方案大致有2種:十六次序和三十二次序［3，4］。通過導航仿真可以發現，兩者在對導航誤差的抑制方面基本上具有相同的效果，下面針對十六次序轉位方案分析轉位誤差與非對稱標度因數誤差的耦合效應。

以導航坐標系東北天坐標系xnynzn作為參考，十六次序轉位方案是指IMU繞zn軸和xn軸(或者yn軸)以一定的次序順序轉過180°，每一次旋轉之間都停留一定的時間ΔT，通過這種不斷地轉停來消除影響導航精度的誤差因素。

單獨看繞天向軸zn軸的旋轉，共有8次，由于轉位誤差的存在，每一次旋轉時都不能精確地轉過180°，為了分析的方便，假設控制轉動時不出現超調，那么，每次轉位時都會離目標位置xn有一個Δθ的誤差角，Δθ相當于轉動的死區，轉位示意圖如圖1所示。

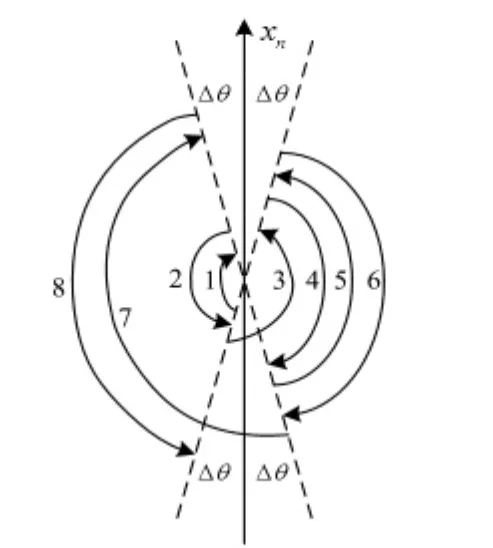
圖1 繞zn轉動過程圖Fig 1 Rotation process around zn axis

由圖1可以看出:在3次序和7次序轉動過程中，xn軸的負向比xn軸的正向多轉過了兩次2Δθ，這就造成了等效非線性標度因數誤差矢量在轉動過程中的空間分布不對稱，表現在導航解算中就會等效地引入常值誤差，通過積分作用引起導航精度的下降，最終體現在經度位置的發散上。

3 仿真分析

仿真條件設定如下:旋轉速度ω=16.7°/s，每個位置停留時間ΔT=10 s，3只陀螺的標度因數不對稱性均為S-gi=1×10-6(i=1，2，3)，所處緯度 L=39.8°，所處經度 λ =116.2°，轉位周期T=332.8 s，每經過一個周期T存儲一次導航數據，導航時間為200 h。當轉位誤差分別為Δθ=6″，12″，18″，24″時，與 Δθ=0″時的導航經度誤差對比圖如圖2、圖3、圖4、圖5所示。

由圖2、圖3、圖4、圖5可以看出:在3只陀螺的非對稱性標度因數相同的條件下，導航經度誤差會隨著轉位誤差的增大而增大，Δθ=6″，12″，18″，24″時的經度誤差分別為Δλ =0.004'，0.008'，0.012'，0.016'，兩者近似呈線性關系。

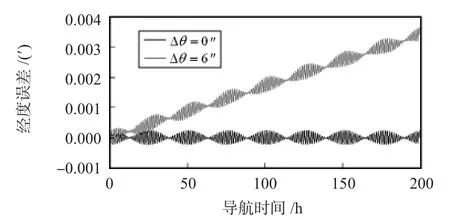
圖2 Δθ=6″與Δθ=0″時的導航經度誤差對比Fig 2 Navigation longitude error contrast when Δθ=6″and Δθ=0″

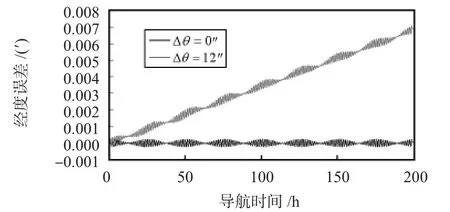
圖3 Δθ=12″與Δθ=0″時的導航經度誤差對比Fig 3 Navigation longitude error contrast when Δθ=12″and Δθ=0″

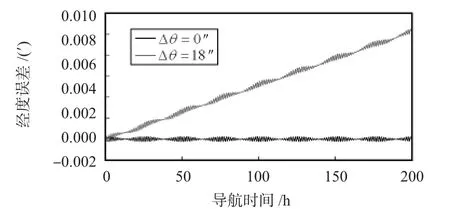
圖4 Δθ=18″與Δθ=0″時的導航經度誤差對比Fig 4 Navigation longitude error contrast when Δθ=18″and Δθ=0″

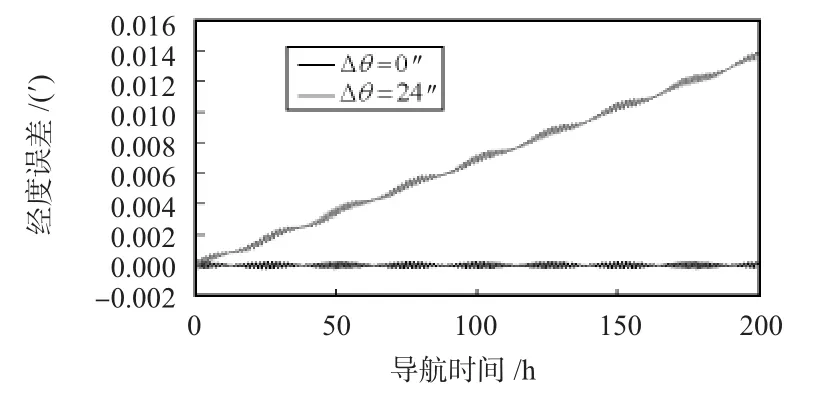
圖5 Δθ=24″與Δθ=0″時的導航經度誤差對比Fig 5 Navigation longitude error contrast when Δθ=24″and Δθ=0″

若保持轉位誤差不變，當增大非線性標度因數誤差時，最終的導航經度誤差會隨著非線性標度因數誤差的增大而增大。當 S-gi=2 ×10-6(i=1，2，3)，Δθ=24″時，200 h 的導航經度誤差會增大到0.03'，如圖6所示。

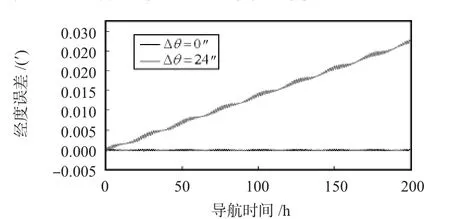
圖6 增大非線性標度因數誤差后的導航結果對比Fig 6 Navigation results contrast after the nonlinear scale factor error increasing

4 結論

通過以上的分析和仿真過程，可以得出以下結論:雙軸旋轉INS轉位誤差會與非線性標度因數誤差發生耦合作用，最終影響導航精度，致使導航經度誤差的積累和發散，并且兩者任何一方的增大都會引起導航經度誤差的增大。因此，在設計雙軸旋轉INS時，要注意選擇非線性標度因數誤差較小的慣性元件，并且采取措施盡量減小轉位誤差，提高轉位的精確度。

［1］Titterton D H，Weston J L.Strapdown inertial navigation technology［M］.2nd ed.American:Published by the American Institute of Aeronautics and Astronautics and the Institution of Electrical Engineers，2004:231-254.

［2］袁保倫.四頻激光陀螺旋轉式慣導系統研究［D］.長沙:國防科技大學，2007:26-28.

［3］張 鵬.激光陀螺捷聯慣導系統旋轉調制技術研究［D］.哈爾濱:哈爾濱工業大學，2010:53-56..

［4］楊 喆.旋轉式捷聯慣導系統誤差分析與轉動方案研究［D］.哈爾濱:哈爾濱工業大學，2010:72-76.