基于遺傳模擬退火算法的注塑機增力機構優化研究
李鐵軍,朱成實,鄢利群,李 新,寧建榮
(沈陽化工大學機械工程學院,遼寧沈陽110142)
基于遺傳模擬退火算法的注塑機增力機構優化研究
李鐵軍,朱成實,鄢利群,李 新,寧建榮
(沈陽化工大學機械工程學院,遼寧沈陽110142)
對注塑機五鉸鏈斜排雙曲肘增力機構進行了運動和力學特性分析,采用遺傳模擬退火算法對該增力機構進行了優化設計,以機構行程比較大、力的放大倍數較大和機構總長較小為目標函數建立了優化數學模型,該優化設計屬于多目標函數優化問題,通過對增力機構實例優化計算與傳統設計方法進行了比較,結果表明行程比增加5.97%,力的放大倍數增加14.10%,機構總長減小5.25%。
遺傳模擬退火算法;優化設計;行程比;增力機構;注塑機
0 前言
五鉸鏈斜排雙曲肘增力機構主要特點是機構剛性大,適合于高速注塑所需的高載荷;運動性能較好,符合注塑工藝的要求;合模速度快,有利于縮短成型周期,提高生產效率;借助機構的自鎖特性鎖緊模具,滿足了其安全、可靠和節能等方面的要求。因此目前該機構是國內外注塑機廣為采用的結構形式,結構如圖1所示。但該結構同時也存在著設計變量繁多,設計計算復雜,設計周期長等問題。因此,以往對增力機構的設計多沿用經驗或類比設計[1],而這樣設計的參數不可能是最佳組合,使其優越性能得不到充分發揮。
解決這種大型復雜優化設計問題,傳統優化方法具有極大的局限性,優化成功率低。遺傳算法是一種模擬生命進化機制的探索和優化方法,與傳統優化方法相比有其獨特優點[3-6]:它以決策變量的編碼作為運算對象而不是對決策變量本身進行處理;直接以目標函數值作為搜索信息,不需要梯度以及其他輔助條件,從而不受函數多峰、不連續、不可微等特性的影響,在群體中具有高適應度值的個體具有較高的在后續代中繁殖和生存;并行地搜索整個種群,而不是進行單點搜索;采用概率轉移策略,而不是確定性地從整個解空間進行求解,可以避免常規優化算法中陷入局部最優解現象。上述基本遺傳算法雖然可以從理論上證明能從概率的意義以隨機的方式尋求到最優解,但是實踐中發現容易出現早熟現象、局部尋優能力差,然而,模擬退火算法卻具有很強的局部搜索能力,結合兩者的優點,在遺傳算法的搜索過程中融入模擬退火算法思想,使最終的算法既具有強大的全局尋優能力,又具有強大的局部尋優能力,從而提高遺傳算法的運行效率和求解質量,這就是遺傳模擬退火算法的基本思想。通過選擇、交叉和變異三種遺傳操作并結合模擬退火算法不斷進化求優,從而找到問題的最優解。
本文在分析了五鉸鏈斜排雙曲肘增力機構的運動及力學特性的基礎上,用遺傳模擬退火算法對合模力為1000kN的增力機構進行了優化設計。注塑機五鉸鏈斜排雙曲肘增力機構優化設計是一種多目標、多變量、多約束求極值問題。

圖1 增力機構結構Fig.1 Structure of force increasing mechanism
1 基于遺傳模擬退火算法的優化模型求解
1.1 基因編碼
由于本優化要求精度較高,因此二進制編碼不能滿足要求,所以采用浮點數編碼。
1.2 初始群體產生
鑒于約束條件影響,在各基因取值范圍內隨機產生優化大小為150的群體。
1.3 適應度函數構建
計算每個個體的適應度,適應度值的大小決定了該染色體被選擇的概率,從而反映適者生存的原則,構建的適應度函數g(x)如式(1)所示。

式中 F(x)——目標函數
gi(x)——約束條件函數
R——懲罰因子
1.4 遺傳操作
按照適應度值對各個染色體進行選擇、交叉和變異等遺傳操作,這些遺傳操作傾向于產生更優秀的染色體,即產生更好的解。通過選擇、交叉和變異等遺傳操作產生一組新的個體,然后獨立地進行各個新個體的模擬退火過程,以其結果作為下一代群體中的個體,反復迭代直到滿足某個終止條件為止。
1.5 模擬退火算法的基本原理及操作
模擬退火算法是一種啟發式的蒙特卡羅方法。這種算法是在給定的模型空間內搜索函數達到全局極小值的最優模型,已用于各種最優化問題計算。模擬退火算法包括以下步驟:(1)給定模型每一個參數的變化范圍,在這個范圍內隨機選擇一個初始模型m0,并計算相應的目標函數值E(m0);(2)對當前模型m0進行擾動產生一個新模型m,計算相應的目標函數值E(m),得到ΔE=E(m)-E(m0);(3)若ΔE<0,則新模型m被接受;若ΔE>0,則新模型按概率P=exp(-ΔE/T)進行接受,T為溫度。當模型被接收時,置m0=m,E(m)=E(m0);(4)在溫度T下,重復一定次數的擾動和接受過程,即重復步驟2和步驟3;(5)緩慢地降低溫度T;(6)重復步驟2和5,直到收斂條件滿足為止。
遺傳模擬退火算法程序流程圖如圖2所示。

圖2 遺傳模擬退火算法程序流程圖Fig.2 Procedure chart of genetic simulated annealing algorithms
2 注塑機增力機構特性分析
根據機構學的分析,確定增力機構的總長度、行程比及力的放大倍數表達式[1],機構原理如圖3所示。

圖3 增力機構原理Fig.3 The principle of force increasing mechanism
2.1 機構總長L
機構總長由式(2)計算。

式中 L1——后肘桿長度,mm
L2——前肘桿長度,mm L4——連桿長度,mm
L5——后肘支桿長度,mm L——機構總長,mm
E——十字頭高度,mm
αmax——最大啟模角,°
θ——斜排角,°
γ——后肘桿夾角,°
2.2 力的放大倍數M
力的放大倍數M由式(3)計算。

式中 α——后肘桿轉角,°
β——前肘桿轉角,°
φ——連桿與水平夾角,°
2.3 行程比R
形成比R由式(6)計算。

式中 Sm——動模板行程,mm
S0——合模油缸活塞行程,mm
3 建立機構優化數學模型
在注塑機設計中,通常要求機構必須滿足以下3方面的要求:(1)機構總長較小;(2)力的放大倍數較大;(3)行程比較大。因此增力機構的優化設計屬于多目標函數優化問題。
3.1 建立目標函數
目標函數如式(9)所示。

式中 W1、W2、W3——多個目標函數之間的權重系數
W1、W2、W3可根據實際生產設計需要調整。
3.2 約束條件
3.2.1 力的放大倍數約束條件
根據實際情況,經過試算,最后確定:M≥23,則力的放大倍數約束函數如式(10)所示。

式中 g1(x)——力的放大倍數約束函數
3.2.2 行程及行程比約束條件
動模板行程應滿足行業標準的要求,又不應超越規格等級,而行程比則沿用以往設計中人們普遍接受并采用的限制條件,300≤Sm≤330,R≥1,則有:

式中 g2(x)——行程下限約束函數
g3(x)——行程上限約束函數
g4(x)——行程比約束函數
3.2.3 機構總長約束條件
在肘桿增力機構的設計中,除了要提高力的放大倍數以及行程比之外,還要保證機構的軸向總長不變,L≤610,如式(14)所示。

式中 g5(x)——行程總長約束函數
3.2.4 自鎖條件約束條件
最大啟模角應滿足條件如式(15)所示。
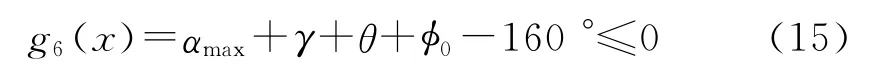
式中 φ0——鎖緊位置時L4與水平方向夾角,°
3.2.5 L1和L2桿長度約束條件
L1和L2桿不僅決定著機構的總長,而且對機構的運動學和力學性能也有較大的影響。通常:0.7≤L1/L2≤0.9,L1≥Sm/2,則有

式中 g7(x)——L1約束函數1
g8(x)——L2約束函數
g9(x)——L1約束函數2
3.2.6 L3、L4和L5桿約束條件
L3和L4桿必須足夠長,以保證機構中的肘桿可以相對回轉,因此必須滿足式(19)。

式中 L3——后支座桿長,mm
dB——B點的回轉直徑,mm
dF——F點的回轉直徑,mm
L4≥(dA+dB)/2,H≥L5+dB/2,則有式(20)、(21)和(22)。

式中 dA——A點的回轉直徑,mm
g10(x)——L5約束函數1
g11(x)——L4約束函數1
g12(x)——L5約束函數2
另外,為了有利于開閉模時力的傳遞,通常還要滿足式(23)和式(24)的約束條件,由式(23)、(24)可得出式(25)、(26)。

式中 φmax——起始位置時L4與水平方向夾角,°
g13(x)——L5約束函數3
g14(x)——L4約束函數2
3.2.7 定義域約束條件
根據式(2)、(4)、(7)、(8),可得式(27)、(28)。

式中 g15(x)——參數定義域約束1
g16(x)——參數定義域約束2
邊界條件約束中,本文取對系統影響較大的8個參數作為設計變量,其余的變量按經驗取為常數。
3.2.8 后肘桿夾角約束條件
根據經驗,后肘桿夾角約束條件如式(29)所示。

3.2.9 斜排角約束條件
斜排角的選取可改善動模板的受力情況,使機構緊湊,一般情況下,約束條件如式(30)所示。

3.2.10 十字頭高度約束條件
為便于結構布置,十字頭高度約束條件應滿足式(31)。

其余變量的邊界約束條件如式(32)、(33)、(34)、(35)、(36)。

3.3 確定設計變量
確定設計變量如式(37)所示。

3.4 增力機構的優化數學模型
增力機構的優化數學模型如式(37)、(38)、(39)、(40)所示。

4 優化設計實例分析
根據經驗或類比的方法可獲得原始參數如下:L1=190,L2=240,L4=75,L5=161,E=140,αmax=110°,θ=4°,γ=20°,機構總長L=610,力的放大倍數Mα=3°=20.37,行程比R=0.97。
在GA算法中,群體大小N=150,交叉概率Pc=0.75,變異概率Pm=0.03,經80代遺傳進化操作。
采用C#編制程序,通過優化計算從獲得一系列Pareto解集中,選擇一組最優化的結構參數,與常規設計進行比較分析,主要優化結果見表1。
優化運算過程中,各個參數沒有發生穿越邊界約束條件現象。最優解與優化前經驗設計解分布情況如圖4。根據表1中的優化結果,將遺傳模擬退火算法優化結果與優化前比較可見:行程比增加5.97%,力的放大倍數增加14.10%,機構總長減小5.25%。同時將遺傳模擬退火算法優化結果與基本遺傳算法優化結果比較:行程比增加2.39%,力的放大倍數增加1.28%,機構總長減小1.70%。從上述比較分析可見:機構總長減小的同時,行程比R及力的放大倍數M都有明顯提高。

表1 主要優化結果Tab.1 Main optimal results

圖4 最優解分布情況Fig.4 Distribution of the optimal solution
5 結論
(1)通過采用遺傳模擬退火算法優化,注塑機的行程比增加5.97%,力的放大倍數增加14.10%,機構總長減小5.25%;
(2)通過采用遺傳模擬退火算法優化提高了增力機構的運動及力學性能,即以低能耗獲得高效率;
(3)遺傳模擬退火算法優化具有較強的可操作性。
[1] 北京化工學院.塑料機械設計[M].北京:機械工業出版社,1982:50-90.
[2] 朱成實,吳 瓊,吳敬東,等.用MathCAD對注射機增力機構進行優化設計[J].機械設計,2005,22(1):56-58.
Zhu Chengshi,Wu Qiong,Wu Jingdong,et al.Using MathCAD to Carry out Optimization Design on Force Increasing Mechanism of Injection Machine[J].Journal of Machine Design,2005,22(1):56-58.
[3] 周 明,孫樹棟.遺傳算法原理與應用[M].北京:國防工業出版社,1999:11-13.
[4] Glodberg D E.Genetic Algorithms in Search,Optimization and Machine Learning[M].Boston:Addison-Wesley,1989:10-20.
[5] Ishibuchi H,T Murata.A Multiobjective Genetic Local Search Algorithm and Its Application to Flowshop Scheduling[J].IEEE Transactions on System,1998,28(3):392-403.
[6] 黃高義,鄒慧君,田永利.基于遺傳算法的連桿機構運動軌跡設計的研究[J].機械設計與研究,2003,19(3):27-31.
Huang Gaoyi,Zou Huijun,Tian Yongli.Research of Movement-trajectory Design of Linkage Mechanism Based on Genetic Algorithm[J].Machine Design and Research,2003,19(3):27-31.
Optimal Research on Force Increasing Mechanism of Injection Machine Based on Genetic Simulated Annealing Algorithms
LI Tiejun,ZHU Chengshi,YAN Liqun,LI Xin,NING Jianrong
(School of Mechanical Engineering,Shenyang University of Chemical Technology,Shenyang 110142,China)
The analysis of motion and mechanical property was carried out on a force increasing mechanism of injection machine which was five hinged incline arranged and double elbowed.A complete optimization design procedure was carried out using genetic simulated annealing algorithms,so as to increase the stroke ratio and the amplification of the force,and to decrease the total length of mechanism.Its optional mathematics model was established.The procedure of optimal design belongs to multi-object optimization problem.The optimal solution of the force increasing mechanism was found with genetic simulated annealing algorithms.Compared with the traditional methods,the stroke ratio was increased by 5.97%,the amplification of the force increased by 14.10%,and the total length of mechanism decreased by 5.25%.
genetic simulated annealing algorithm;optimal design;stroke ratio;force increasing mechanism;injection machine
TQ320.5
B
1001-9278(2012)02-0099-05
2011-09-11
聯系人,litiejun780920@sina.com
(本文編輯:劉本剛)

