晶界對近片層TiAl高溫動態力學行為的數值模擬

盧 山，李子然，昝 祥

(1. 中國科學技術大學 近代力學系 中國科學院材料力學行為和設計重點實驗室，合肥 230027；2. 合肥工業大學 材料科學與工程學院，合肥 230009)

晶界對近片層TiAl高溫動態力學行為的數值模擬

盧 山1，李子然1，昝 祥2

(1. 中國科學技術大學 近代力學系 中國科學院材料力學行為和設計重點實驗室，合肥 230027；2. 合肥工業大學 材料科學與工程學院，合肥 230009)

基于晶體塑性理論，給出了同時考慮位錯滑移、形變孿晶和晶界變形的近片層組織TiAl本構模型；在此基礎上，建立基于Voronoi算法的近層片TiAl三維多晶有限元模型，并在晶粒交界處引入殼單元來描述晶界；利用上述有限元模型，對不同溫度(室溫、500和700 ℃)和不同拉伸應變率(10?3、320、800和1 350 s?1)下近層片TiAl的塑性力學行為進行數值模擬。結果顯示：模擬得到的應力塑性應變曲線與試驗結果吻合較好，能夠反映近層片TiAl在不同溫度和應變率下的材料響應；由于晶界的存在，晶粒內的應力分布會發生明顯改變，晶界附近產生一定的應力集中。此外，晶界對孿晶存在一定的阻礙作用，使得晶界附近實體單元的孿晶體積分數要略低于多晶整體的平均孿晶體積分數。

鈦鋁金屬間化合物；Voronoi算法；晶界；動態拉伸；有限元

TiAl基金屬間化合物是一種新型的輕質高溫結構材料，具有低密度、高比強度、高比模量、優異的抗氧化、抗鈦火及抗蠕變性能等特性，且在高溫下仍能保持較高的比強度及比剛度，在航空、航天和汽車等領域具有廣闊的應用前景[1?2]。由于試驗技術上的困難，目前對TiAl基金屬化合物動態力學行為的研究多集中在SHPB裝置上所展開的動態壓縮力學性能的研究[3]。昝祥[4]采用旋轉盤式間接桿?桿型沖擊拉伸實驗裝置(一種SHTB裝置)，較全面系統地研究等軸(Near gamma, NG)、雙態(Duplex, DP)和近片層(Near lamellar,NL) 3種組織形態的TiAl在不同溫度下的動態拉伸力學性能。但TiAl動態拉伸試驗在技術上仍存在很多困難，需要以數值計算代替部分實驗工作。

近年來，對TiAl力學行為的數值計算已進行了一系列的研究[5?10]，主要集中在室溫準靜態下，模型也比較簡單。KAD等[5]率先基于晶體塑性理論來模擬全片層(Fully lamellar, FL)組織TiAl，將片層晶群的變形方式分為軟剪切模式和硬剪切模式，由于采用了過于簡化的模型，計算值與試驗曲線之間存在較大偏差。WERWER和CORNEC等[6?7]研究了TiAl的彈塑性、斷裂性以及各向異性等力學性能，根據FL TiAl晶粒的長度與厚度比值大小的不同，建立了簡化的三維模型，但是模型中晶粒數目很少，不能夠反映真實材料中晶粒隨機取向的影響。MARKETZ等[8?9]雖然建立計入位錯滑移和形變孿晶對其塑性變形的貢獻，其工作僅模擬 TiAl室溫下準靜態范圍內的拉伸和壓縮力學行為。最近，王東[10]發展了更為合理的、同時考慮位錯滑移和形變孿晶作用、并考慮溫度影響的TiAl單晶本構模型，能夠比較好地模擬NG TiAl在不同溫度和應變率下的材料響應。但以上工作都未引入晶界的效應。

晶界對于 TiAl基金屬間化合物(尤其是 NL TiAl和 FL TiAl)力學行為有很大的影響[4,11?12]。昝祥[4]對NL TiAl拉伸斷裂試件進行了TEM觀測，并與NG TiAl的TEM像進行相比，發現在相同的變形量下，NL TiAl高溫下的試件中形變孿晶和層錯的密度要小，說明部分形變是由晶界的運動造成的。CHANG[11]的研究表明，片層TiAl晶界的模量達到晶粒內部模量的7倍，這會導致變形的不均勻性。SIMKIN等[12]觀測到TiAl變形過程中位錯會在晶界處堆積，并指出γ-TiAl中微觀裂紋的產生是由于晶界對形變孿晶的阻斷。綜上所述，在TiAl的數值計算中有必要考慮晶界的影響。

本文作者將基于晶體塑性理論，給出同時考慮位錯滑移、形變孿晶和晶界變形的NL TiAl本構模型。在此基礎上，建立基于Voronoi算法的NL TiAl三維多晶有限元模型，并在晶粒交界處引入殼單元來描述晶界。利用上述有限元模型，對不同溫度(室溫、500和700 ℃)和不同拉伸應變率(10?3、320、800和1 350 s?1)下近片層組織的Ti-46.5Al-2Nb-2Cr(簡稱NL TiAl)的彈塑性力學行為進行模擬，并重點考察晶界效應及其對于孿晶演化的影響。

1 TiAl的晶體塑性本構模型

1.1 晶粒本構模型

TiAl基金屬間化合物是由 γ-TiAl和的α2-Ti3Al(體積分數小于 10%)組成。γ-TiAl中位錯滑移主要有{111}1/2〈110]普通位錯和{111}〈101]超位錯；α2-Ti3Al中，主要有柱面{1100}〈11 2 0〉、底面{0001}〈11 2 0〉和錐面{1 121}〈1 1 26〉三組滑移系[4]。由Schmid定律，位錯滑移系α上的 Schmid分解剪應力 τ(α)采用如下定義

式中： m*(α)為滑移系α現時構型中滑移方向的矢量，s*(α)為滑移系α現時構型中滑移面上垂直于滑移方向的矢量，j為Jacobi行列式，σ為Cauchy應力張量。滑移系α上的剪切應變率由 Schmid分解剪應力 τ(α)決定[10]

式中：0γ˙為參考切應變率；m為應變率敏感系數，反映應變率影響；)(αg 為當前強度，反映硬化規律，任一滑移系上應變的變化都會對滑移系α的強度)(αg產生影響，可表示為

式中：αβh為滑移硬化系數，它取決于當前的位錯密度和位錯組態。當βα≠時，αβh稱為潛在硬化模量，采用如下的簡化公式來確定

式中：q為一常數，取值范圍為1.0～1.4。當α=β時，hαβ=hαα稱為自硬化模量，可采用如下的公式計算[8]：

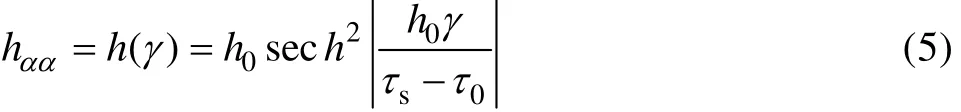
式中：h0為初始硬化模量，τs為單晶第一階段飽和流動應力，τ0為滑移系初始臨界切應力(CRSS)，γ是所有滑移系上剪應變的總和，即

由于 γ-TiAl的面心四方(FCT)晶體結構對稱度低且可動滑移系少，形變孿晶成為位錯滑移的有效補充[4?10]，且現有的試驗也表明動態下有利于孿晶的產生[4]，因此有必要考慮形變孿晶的影響。在某一特定體積分數 f(β)下的孿晶β所產生的平均剪切應變可以寫成 γTf(β)，其中γT為孿晶切應變[9]。孿晶平均切應變率 γ˙(β)就可用孿晶體積分數變化率 f˙(β)寫成

孿晶體積分數的演化方程可以采用與位錯滑移相似的 Schmid定律進行描述，但由于孿晶和位錯變形機制不同，必須對其演化條件給予以一定的限制[4,9]。FISCHER等[13]指出 L10結構在(111)面上一般只產生1/6〈112]形式的孿晶，只有分解切應力沿孿晶正方向達臨界值后，形變孿晶才會產生。在此，計算孿晶體積分數的演化采用如下方程：

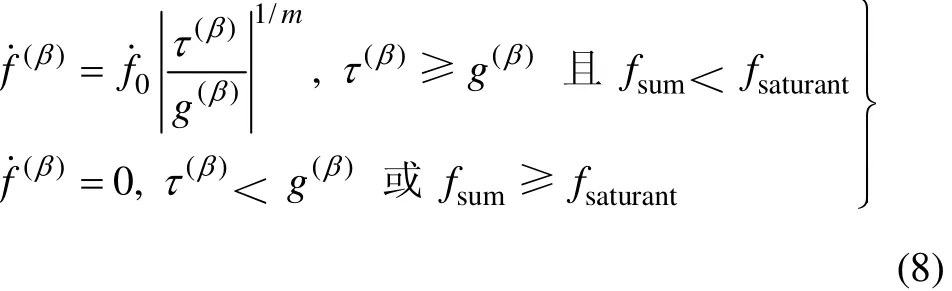
式中：τ(β)為形變孿晶的分解剪應力， g(β)為臨界剪應力， f˙0為參考體積分數變化率，fsum為孿晶累積體積分數，fsaturant為孿晶飽和體積分數。

由式(2)、(7)和(8)，最終可以得到晶粒內部位錯和孿晶共存時的塑性變形率(Lp)[8]

式中： P(α)和 P(β)分別為位錯和孿晶的Schmid方向因子。

1.2 晶界本構模型

一般情況下金屬多晶體的晶界厚度很薄，盡管如此，晶界對于金屬材料的總體性能有較大的影響，本文作者將晶界本構看作是由一個滑移系和一個擴容系所組成的本構模型[14]，滑移系的滑移面為晶界面，滑移方向是沿著晶界面的切線方向，擴容系是指晶界在晶界面的法線方向上也可以產生應變。在此，由程序自動判斷并計算每個晶界面上初始時刻滑移系的滑移方向和擴容系的應變方向，并將相應的數值輸入到有限元模型中。

晶界的滑移變形采用與位錯滑移相似的 Schmid定律進行描述。擴容系上的分解剪應力 τ(N+1)表示為

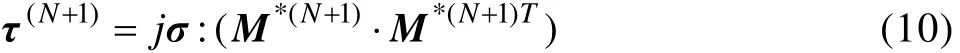
式中： M*(N+1)是第N+1步現時構型晶界面的法向，擴容系的硬化方程也采用了與晶粒的位錯滑移相似的方程。

上述同時考慮位錯滑移、形變孿晶和晶界效應的晶體塑性本構模型已通過編制用戶定義材料子程序在商用軟件 ABAQUS6.8/Standard中實現，其中位錯滑移、形變孿晶部分主要參考了文獻[9]的研究結果。

1.3 計算中參數的選取

在本計算中，γ-TiAl在不同溫度下的彈性常數可由文獻[15]得到，文獻中給出了彈性常數隨溫度變化的二次擬合結果 Cij= C0+ AT + B T2，其中C0、A、B為彈性參數，如表1所列。

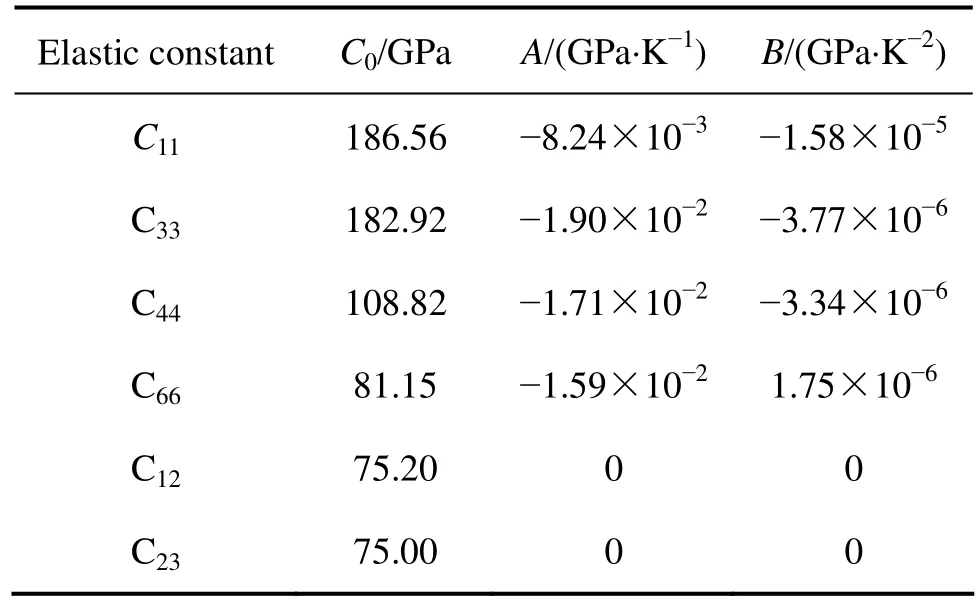
表1 在不同溫度下γ-TiAl的彈性常數Table 1 Elastic constants of γ-TiAl at different temperatures

文獻[9]僅給出2α-Ti3Al在0 K下的彈性常數，鑒于2α相晶粒總體積分數不到10%，本文作者忽略溫度對2α-Ti3Al彈性常數的影響。由于缺乏準確的試驗數據，在計算模型中暫取晶界殼單元的體積分數為10%，并假設晶界為一種各項同性材料。根據文獻[12]對片層TiAl的微觀組織觀測研究，可知晶界的模量約為晶粒內部模量的7倍，因此暫取晶界的模量E為7倍的C11，其中 C11為同一工況下的 γ-TiAl的一個彈性常數[16]，泊松比取0.3。

由于 TiAl臨界剪切應力對應變率和溫度的變化十分敏感，且受材料中的雜質成分和含量的影響很大，這里參考 TiAl單晶壓縮實驗得出的不同溫度下滑移系的CRSS的變化趨勢[15]，并結合運算，得出使模擬結果與實驗結果較為吻合的參數，下面給出擬合得到的各滑移系和孿晶的臨界剪切應力隨溫度T變化的函數形式：τ0=A1exp(B1T)+C1exp[D1(T?T0)2]，其中 A1、B1、C1、D1和T0為常數，如表2所列。

不同溫度下的位錯和形變孿晶的應變率敏感系數的擬合結果可根據文獻[17]所給出的變化趨勢并結合試算結果得到。由于缺乏相關數據，為簡單計算，在此暫取晶界滑移系和擴容系的應變率敏感系數與位錯一致。

位錯：

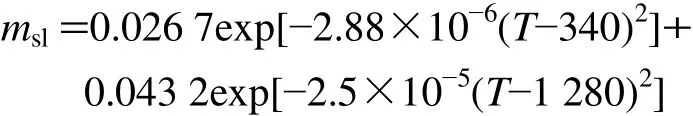
孿晶：

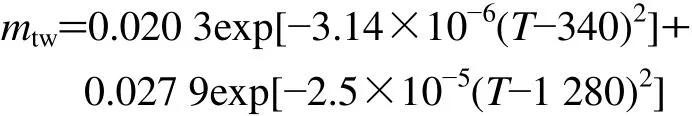
其他參數則參考文獻[5?10]計算過程中的取值，并結合本運算結果得到。其中，位錯滑移、晶界滑移和擴容的參考切應變率0γ˙=0.000 1；孿晶參考體積分數變化率0f˙=0.000 14；各滑移系第一階段飽和切應力τs取為1.3倍的初始臨界剪切應力；忽略溫度對初始硬化模量h0的影響，對γ-TiAl，普通位錯、超位錯、孿晶、晶界滑移和擴容的h0分別取400、500、400、400和400 MPa；對α2-Ti3Al，柱面、底面和錐面滑移h0分別取400、600和900 MPa。

2 基于 Voronoi算法的包含晶界的TiAl多晶有限元模型

2.1 基于Voronoi算法的NL TiAl多晶有限元模型的

建

立

為了引入晶界并建立更加真實合理的NL TiAl多晶有限元模型，本文作者采用一種基于 Voronoi算法隨機產生晶粒的方法[18]。Voronoi多面體模型的實現主要包括如下3步：首先，一個發芽的過程，在幾何模型上隨機產生 n個晶粒的中心六面體小單元；其次，計算各個小單元到n個中心小單元的歐幾里得距離，這一步可以考慮為從晶粒中心開始長大，根據各個小單元到中心小單元的歐幾里得距離的比較，把各個單元歸類到其距離最近的中心單元所在的晶粒，晶粒的平均尺寸是由模型的尺寸和晶粒的數目決定的，通過以上算法建立模型以后，邊界也就出現了，就是Voronoi多面體內晶粒之間的分界面，如圖1所示；最后，由于同一晶粒內的原子緊密排布且具有相同的取向，將同一個晶粒內的所有小單元都賦予相同的取向。

圖1 某25晶粒模型Fig. 1 Model of 25 grains

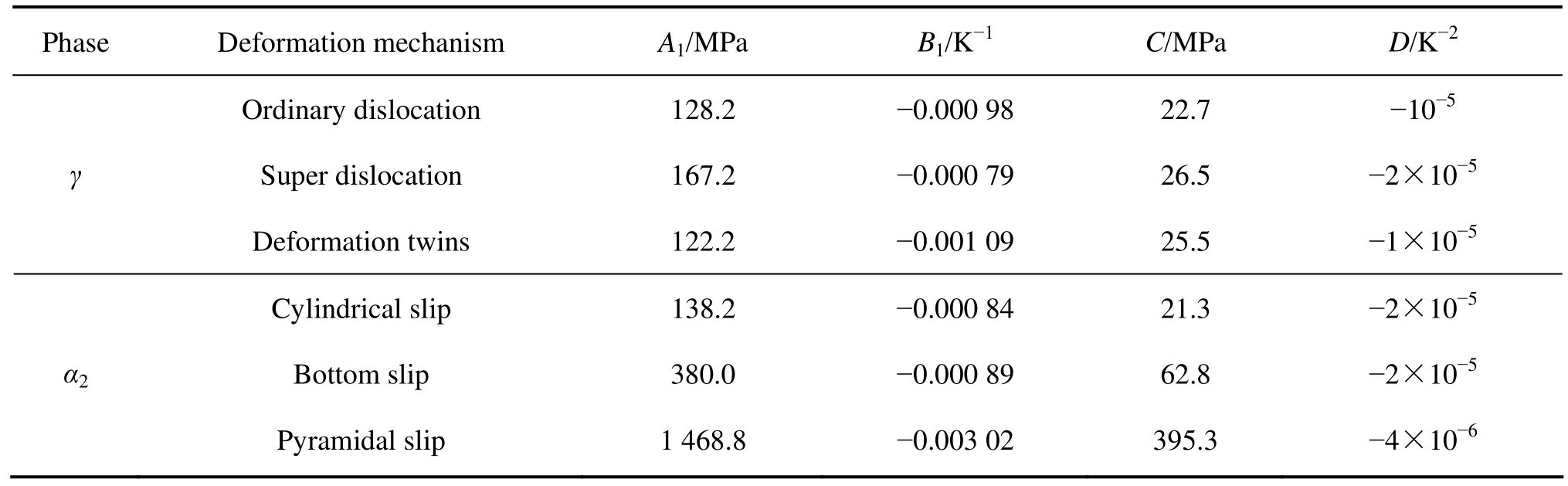
表2 擬合的臨界剪切應力隨溫度T變化的函數參數Table 2 Simulated parameters of critical shear stress vs temperature (T0=965 K)

2.2 TiAl晶界的引入

在以上晶粒幾何模型建立之后，經過如下算法實現在晶粒交界處引入殼單元來描述晶界。首先對每個小單元按順序提取；然后判斷這個小單元與其相鄰的小單元是否屬于同一晶粒，若相鄰兩小單元不屬于同一晶粒，則將這兩個小單元的共用面定義為晶界面；最后通過共用節點的方法，在兩個晶粒交界處添加殼單元，如圖 2所示。如此就建立了一個基于 Voronoi算法的包含晶界的TiAl有限元模型。

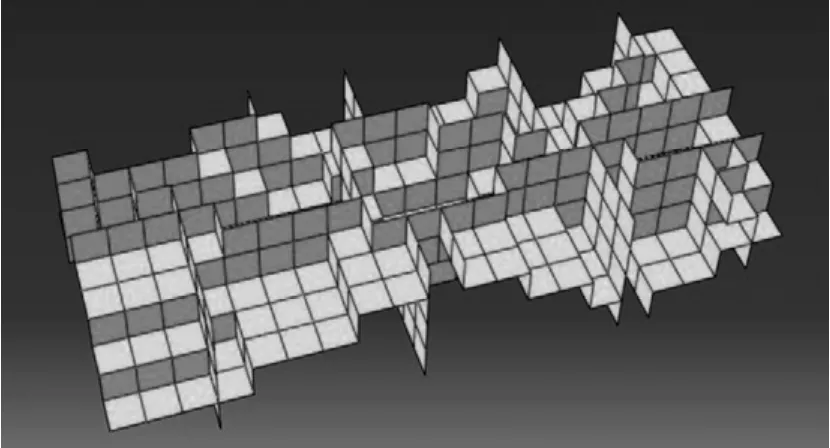
圖2 圖1模型中對應的殼單元Fig. 2 Shell elements corresponding to Fig. 1

在具體計算晶界時采用了考慮橫向剪切變形的厚殼，定義其厚度與跨度的比值1/10，并且采用適合模擬厚殼問題的4節點S4殼單元。在采用UMAT子程序的情況下，Abaqus無法通過輸入文件提供的信息計算出殼單元橫向剪切剛度，需要預先設定。由ABAQUS 6.8 Documentation[19]可知橫向剪切剛度的計算公式可表示為

式中：A是殼面積，t是殼的厚度。

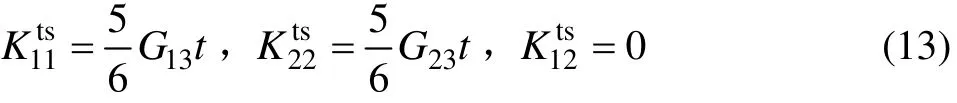
式中：G13和G23是材料在離面方向上的剪切模量，5/6是一個剪切修正系數。

綜上所述，本文作者已經基于 Voronoi算法建立了包含晶界的NL TiAl多晶有限元模型，模型中的每個晶粒的大小、形狀、空間分布都是隨機產生。以上程序均已經在MATLAB 6.5中實現，經MATLAB計算輸出晶粒結構相應的信息，再用于修改 ABAQUS中相應的模型部分。

3 計算結果和討論

3.1 模型的有效性評估

本文作者建立了如圖3的由六面體單元組成的有限元多晶模型，由γ相和α2相(總體積分數略小于10%)晶粒在其中隨機分布組成。本模擬的NL TiAl材料與文獻[4]中的相同，通過其金相圖片對晶粒尺寸的大小進行了估算，得到晶粒平均尺寸約為60 μm。六面體單元中局部坐標的取向代表了晶粒的取向，局部坐標的取向用歐拉角進行表示[20]，通過對3個歐拉角隨機賦值，即可產生隨機取向，但同一個晶粒內的所有單元都被賦予相同的取向。在模擬變形時，對模型的一個面施加固定的邊界條件，對另外一個面施加速度邊界條件以實現不同應變率的加載。

圖3 多晶有限元模型Fig. 3 Polycrystalline model

由于 Voronoi算法所建立的晶粒大小、形狀、空間分布以及晶粒的取向都是隨機分布的，晶粒數目比較少時必然會導致計算結果重復性較差，因此，需要考評所采用模型計算結果的可靠性。在保證晶粒平均尺寸不變的前提下，對不同大小的模型如640單元25晶粒、2 560單元100晶粒、5 120單元200晶粒和10 240單元400晶粒進行了試算，結果如圖4所示。從圖4可以看出，當單元數達到5 120以上時，應力應變曲線之間的差別已經很小(小于 2%)。圖 5給出5 120單元200晶粒時3種不同模型(只是隨機種子不同，算法和分布概率仍然相同)的計算結果，可以看出此時的漲落誤差也已經很小。綜合考慮計算精度和計算效率，本模擬中最終采用幾何尺寸為 0.1 mm×0.2 mm×0.5 mm的5 120單元200晶粒的三維多晶模型進行后續的計算。

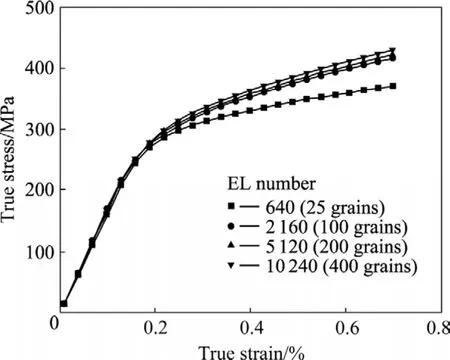
圖4 不同尺寸模型的計算結果的比較Fig. 4 Comparison of results of different models

圖5 200晶粒3種模型計算結果的比較Fig. 5 Comparison of calculation results of three 200 grains models

3.2 計算結果和討論

圖6 不同溫度和拉伸應變率下NL TiAl應力—應變曲線的實驗與模擬結果對比Fig. 6 Comparison of simulated with experimental results of stress—strain curves of NL TiAl under different temperatures and strain rates

本文作者采用上述多晶有限元模型，對文獻[4, 21]中室溫、500 ℃和700 ℃下應變率為10?3、320、800和1 350 s?1的12種拉伸工況進行了模擬，并將應力—塑性應變曲線與文獻[4, 21]中的實驗結果進行了比較。從圖6的結果可以看出：1) 相同溫度下，近層片TiAl在動態加載(320、800和1 350 s?1)下的強度明顯高于準靜態(10?3s?1)加載下的強度；而在動態加載范圍內，由于應變率變化相對較小(320~1 350 s?1，應變率僅增大了3倍)，材料的強度沒有發生明顯的變化，而本文作者所建立的模型較好地反映出不同溫度下近層片 TiAl的應變率強化特性。2) 在同一應變率下，高溫工況屈服強度明顯低于室溫，即近層片TiAl呈現出明顯的高溫軟化現象。模擬結果很好地體現了試驗中出現的這一特性。3) 各工況下計算所得屈服后的硬化趨勢與基本實驗相符，可見模擬能較好反映出近層片TiAl的應變硬化特性，但在高溫工況下塑性應變比較大時，計算結果與實驗結果存在一定的偏差，這可能是由于本文作者對于近層片 TiAl在高溫下的變形機理考慮的還不夠完善造成的。總體上說，本模擬得到的應力塑性應變曲線與試驗結果吻合較好。

3.3 晶界對NL TiAl力學行為的影響

NL TiAl在晶界處會產生應力集中[12]，為了考評模型中的晶界對應力分布的影響，本文作者對室溫準靜態拉伸試驗工況的計算結果進行了分析；分別計算了包含和不含晶界單元的兩種情況，然后對靠近同一晶粒交界面的單元應力進行了對比。結果發現，包含晶界單元時，晶粒交界處的一些單元Mises應力可以達到 460 MPa，約為該晶粒平均值(350 MPa)的 1.3倍；而后者晶粒內最大Mises應力值約為晶粒平均值的1.15倍且分布比較均勻。上述計算結果表明，晶界的引入會改變晶粒的應力分布，且在晶界附近會產生一定的應力集中。

形變孿晶是 NL TiAl的主要塑性變形機制之一[10]，以下將研究形變孿晶對塑性變形的影響以及晶界對形變孿晶體積分數演化的影響。在本模擬中，分別統計了晶界附近實體單元(晶界相鄰的一層實體單元)的孿晶體積分數和整體模型的平均孿晶體積分數，圖7所示為4個工況下(室溫準靜態；室溫320 s?1；

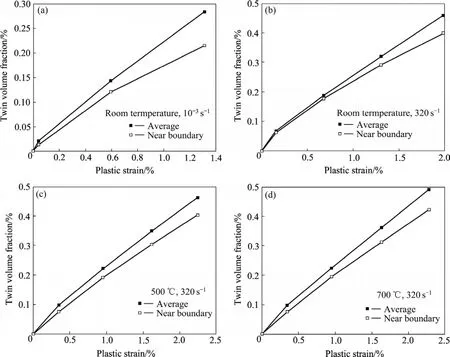
圖7 4個工況下晶界附近的孿晶體積分數與整體模型的平均孿晶體積分數的對比Fig. 7 Volume ratio of deformation twin near grain boundaries vs average value of deformation twin of whole model

500 ℃、320 s?1；700 ℃、320 s?1)孿晶體積分數隨塑性應變的關系曲線，而其它工況結果類似。由圖7可以看出：1) 在各工況下，孿晶體積分數隨塑性應變的增加而增加，說明形變孿晶在NL TiAl的塑性變形過程中一直起作用，這與文獻[9]的報道一致；2) 晶界附近實體單元的孿晶體積分數均略低于整體模型平均的孿晶體積分數，說明晶界對形變孿晶有一定的阻礙作用。

4 結論

1) 基于晶體塑性理論，給出了同時考慮位錯滑移、形變孿晶和晶界變形的近片層TiAl本構模型。在此基礎上，建立了基于Voronoi算法的NL TiAl三維多晶有限元模型，并在晶粒交界處引入殼單元來描述晶界。

2) 利用上述有限元模型，對不同溫度(室溫、500℃和 700 ℃)和不同拉伸應變率(10?3~1 350 s?1)下 NL TiAl的彈塑性力學行為進行了數值模擬。結果顯示，模擬得到的應力應變曲線與試驗結果吻合的較好，能夠很好地反映近片層 TiAl在不同溫度和應變率下的材料響應，驗證了該近片層 TiAl有限元模型的可靠性。

3) NL TiAl有限元模型在加入晶界殼單元后，晶粒內的應力分布會發生明顯的改變，且在晶界附近會產生一定的應力集中。此外，晶界對于孿晶存在一定的阻礙作用，使得晶界附近實體單元的孿晶體積分數要略低于多晶整體的平均孿晶體積分數。

REFERENCES

[1] 顏鳴皋, 吳學仁, 朱知壽. 航空材料技術的發展現狀與展望[J]. 航空制造技術, 2003, 12: 19?25.YAN Ming-gao, WU Xue-ren, ZHU Zhi-shou. Recent progress and prospects for aeronautical material technologies[J].Aeronautical Manufacturing Technology, 2003, 12: 19?25.

[2] 王 剛, 徐 磊, 崔玉友, 楊 銳. 粉末冶金TiAl基合金高溫變形行為及其本構模型[J]. 中國有色金屬學報, 2010, 20(1):269?273.WANG Gang, XU Lei, CUI Yu-you, YANG Rui. High temperature deformation behavior of powder metallurgy TiAl alloy and its constitutive model[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(1): 269?273.

[3] WANG Yu, LIN Dong-liang, KIM Y W. High strain-rate tensile properties of a TiAl alloy in duplex and fully lamellar microstructural forms[J]. Transactions of Nonferrous Metals Society of China, 1999, 9(3): 437?441.

[4] 昝 祥. TiAl基金屬間化合物高溫動態力學行為基變形機理研究[D]. 合肥: 中國科學技術大學, 2008: 18?94.ZAN Xiang. Dynamic mechanical behavior and deformation mechanism of TiAl intermetallics at elevated temperatures[D].Hefei: University of Science and Technology of China, 2008:18?94.

[5] BIMAL K K, MING D, ROBERT J A. Numerical simulations of stress-strain behavior in two-phase α2+γ lamellar TiAl alloys[J].Materials Science and Engineering A, 1995, 192/193: 97?103.

[6] WERWER M, CORNEC A. Numerical simulation of plastic deformation and fracture in polysynthetically twinned(PST)crystals of TiAl[J]. Computational Materials Science, 2000, 19:97?107.

[7] WERWER M, CORNEC A. The role of superdislocations for modeling plastic deformation of lamellar TiAl[J]. International journal of plasticity, 2006, 22: 1683?1698.

[8] MARKETZ W T, FISCHER F D. Computational modeling and experimental study of the deformation behavior of γ-TiAl-based alloy[J]. Advanced Engineering Materials, 2000, 2(10):662?666.

[9] MARKETZ W T, FISCHER F D, CLEMENS H. Deformation mechanisms in TiAl intermetallics—Experiments and modeling[J]. International Journal of Plasticity, 2003, 19:281?321.

[10] 王 東. 高溫動態拉伸下NG TiAl彈塑性力學行為的數值模擬[D]. 合肥: 中國科學技術大學, 2009: 1?20.WANG Dong. Simulation of dynamic mechanical behavior of NG TiAl at elevated temperature[D]. Hefei: University of Science and Technology of China, 2009: 1?20.

[11] CHANG S F. A micromechanics study of lamellar TiAl[J].Experimental Mechanics, 2006, 46: 173?178.

[12] SIMKIN B A, CRIMP M A, BIELER T R. A factor to predict microcrack nucleation at γ-γ grain boundaries in TiAl[J]. Scripta Materialia, 2003, 49: 149?154.

[13] FISCHER F D, SCHADEN T, APPEL F. Mechanical twins,their development and growth[J]. European Journal of Mechanics, 2003, 22: 709?726.

[14] 潘文科, 張永偉, 王自強. 考慮晶界效應的多晶體有限變形分析[J]. 固體力學學報, 1996, 17(3): 189?199.PAN Wen-ke, ZHANG Yong-wei, WANG Zi-qiang. The finite element deformation analysis of polycrystalline considering grain boundary effect[J]. Acta Mechanica Solida Sinica, 1996,17(3): 189?199.

[15] HE Y, SCHWARZ R B. Elastic constants and thermal expansion of single crystal γ-TiAl from 300 to 750 K[J]. Materials Science and Engineering A, 1997, 239/240: 157?163.

[16] 馮 端. 金屬物理學[M]. 北京: 科學出版社, 2000: 351?363.FENG Duan. Metal physics[M]. Beijing: Science Press, 2000:351?363.

[17] HINUI, MATSUMURO M, WU D H. Temperature dependence of yield stress, deformation mode and deformation structure in single crystals of TiAl (Ti-56 at.% Al)[J]. Philosophical Magazine A, 1997, 75(2): 395?423.

[18] FABRICE B, LUC D, DOMINIQUE J. GEORGES C.Intergranular and intragranular behavior of polycrystalline aggregates[J]. International Journal of Plastic, 2001, 17:513?536.

[19] Abaqus Inc. Abaqus 6.8 documentation(v6.8)[G]. RI, USA:Hibbit, Karlsson and Sorensen, 2008.

[20] 黃 文. 純鈦高溫動態拉伸力學性能研究[D]. 合肥: 中國科學技術大學, 2006: 57?87.HUANG Wen, Study on the dynamic behavior of polycrystalline titanium at elevated temperature[D]. Hefei: University of Science and Technology of China, 2006: 57?87.

[21] 昝 祥, 汪 洋, 夏源明. 三種微觀組織的 Ti-46.5Al-2Nb-2Cr高溫動態力學行為的實驗研究[J]. 實驗力學, 2008,23 (6): 477?484.ZAN Xiang, WANG Yang, XIA Yuan-ming. Experimental study of Ti-46.5Al-2Nb-2Cr with three different microstructures under elevated temperatures and high strain rate[J]. Journal of Experimental Mechanics, 2008, 23(6): 477?484.

Numerical simulation of dynamic mechanical behavior of near lamellar TiAl at elevated temperature with influence of grain boundary

LU Shan1, LI Zi-ran1, ZAN Xiang2
(1. CAS Key Laboratory of Mechanical Behavior and Design of Materials, Department of Modern Mechanics,University of Science and Technology of China, Hefei 230027, China;2. School of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China)

Based on the rate dependent crystal plasticity theory, a constitutive relationship of near lamellar TiAl was presented to account for the influence of dislocation slip, twinning evolution and grain boundary movement. With the help of the Voronois arithmetic, a three-dimensional polycrystalline finite element framework, in which the shell elements were used to describe the grain boundaries, was constructed for the implementation of the proposed constitutive model.Numerical simulations of the plastic mechanical behavior of near lamellar TiAl under temperatures of room temperature,500 ℃, 700 ℃ and tensile strain rates of 10?3s?1, 320 s?1, 800 s?1and 1 350 s?1were conducted, subsequently. The results drawn from the simulations agree well with the experimental data. The influence of grain boundary on the mechanical behavior of the near lamellar TiAl was also investigated. The results show that the stress distribution within a grain is significantly changed by the grain boundary, and certain stress concentration appears near the grain boundary.In addition, the calculated results also show that the grain boundary can obstruct the twinning evolution, leading to the volume ratio of deformation twinning around the grain boundaries smaller than that of the whole model.

TiAl intermetallics; Voronois arithmetic; grain boundary; dynamic tensile; finite element

TG146.2

1004-0609(2012)02-0379-09

國家自然科學基金資助項目(10702068, 10902106)

2011-02-11；

2011-05-23

李子然，副教授，博士；電話：0551-3601236；E-mail: lzr@mail.ustc.edu.cn

(編輯 龍懷中)