含多偏差變元Rayleigh型p-Laplacian方程周期解的存在性

陳仕洲

（韓山師范學院數學與應用數學系，廣東潮州 521041）

1 引言及引理

關于具有偏差變元的p-Laplacian微分方程周期解存在性研究已有許多成果[1-5]，例如文獻[4]、文獻[5]分別研究了一類具偏差變元的Lienard型方程

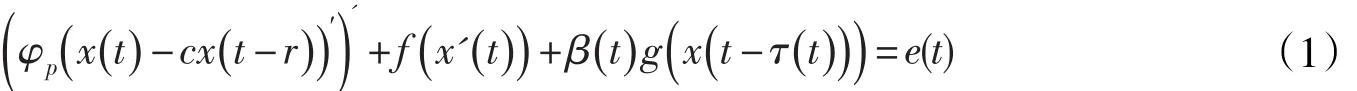
和

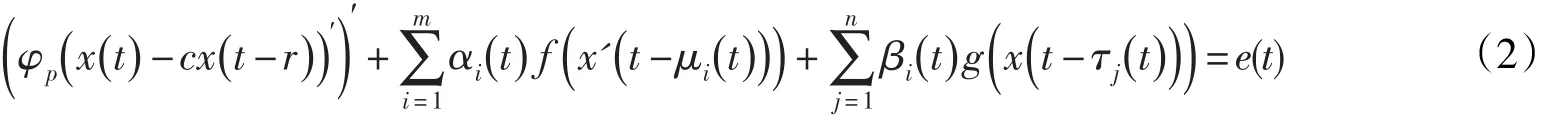
周期解存在性.本文將利用重合度理論，研究一類含有多個偏差變元高階p-Laplacian微分方程

存在周期解的問題，所得結果推廣和改進了文獻[5]的結果.這里φp(x)= | x|p-2x,p＞1,k,m,n都是正整數，c,r∈R，且 | c|≠1αi,μi,βj,τj,f,g,e∈C(R,R)都是周期為T＞0的函數.

全文約定：

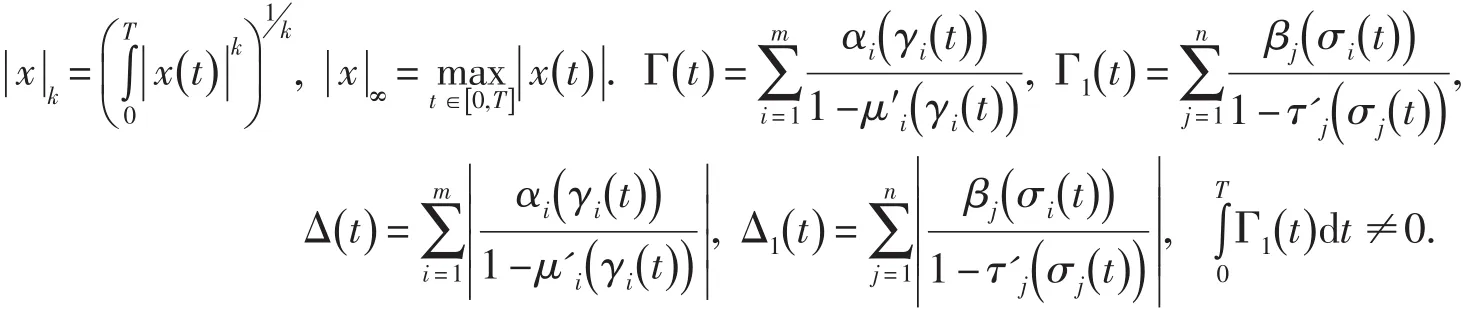
其中 γi(t),σj(t)分別是t-μi(t),t-σj(t)的反函數，i=1,2,…,m;j=1,2,…,n.

設 CT={φ:φ ∈C(R,R),φ(t+T)≡φ(t)} ， 范 數間.定義算子

將方程（3）改寫為

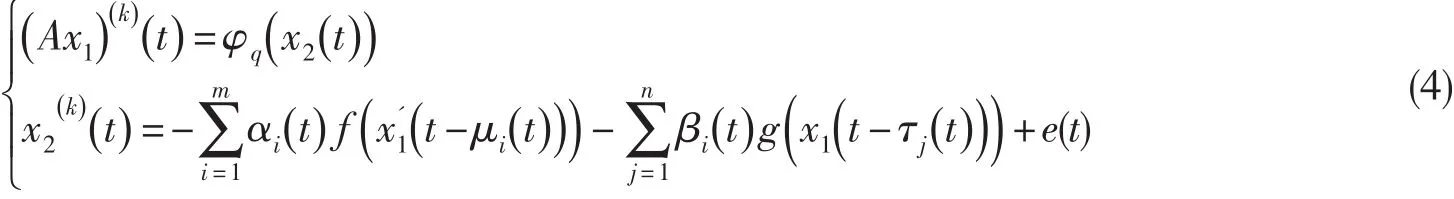
定義算子

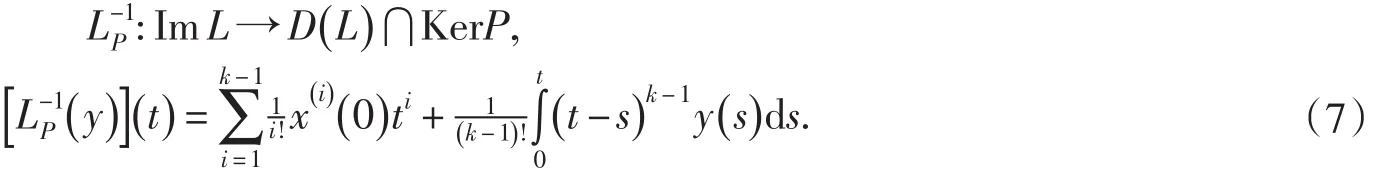
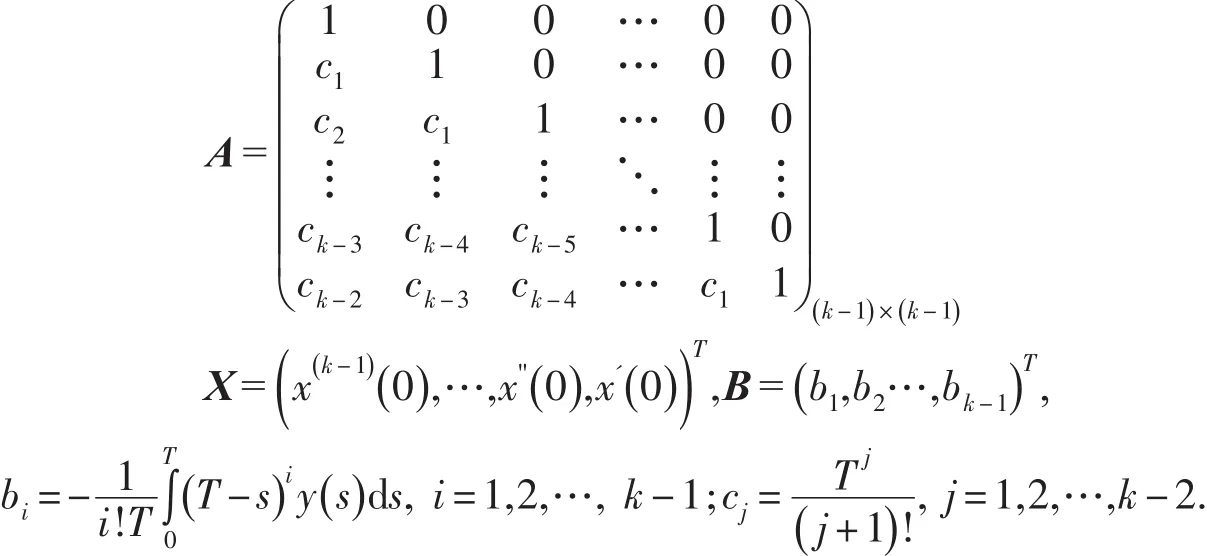
引理1[6]（Mawhiny延拓定理）設X,Y都是Banach空間，L:D(L)?X→Y是指標為零的Fredholm算子，Ω?X為有界開集，N→Y在上是L-緊的.若下列條件成立(1)Lx≠λNx,?x∈?Ω?D(L),λ∈(0,1)，(2)QNx≠0,?x∈?Ω?ker(L)，

(3)deg{JQN,Ω?ker(L),0}≠0,其中J:Im Q→Ker L為同構.則方程Lx=Nx在Ωˉ?D(L)中有解.

引理2 如果x∈Ck(R ,R),x(t +T)≡x(t),且∈[0 ,T],則

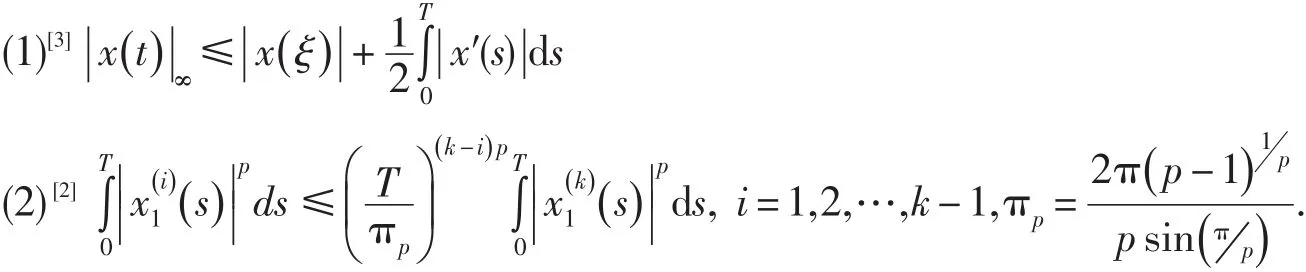
引理3[7]如果 ||c≠1，則A在CT上存在有界連續逆A-1，且?u∈CT,則

引理4[8]如果 g則g(v ( t))∈C,其中v(t)為t-τ(t)的反函數.T

2 主要結論

定理1 設

(H 1)?A,B∈(0 ,+∞) ,0＜α≤p-1,s.t.?y∈R, | f(y) |≤A| y|α+B.

(H 2)(1) ?d,g1,g2∈(0 ,+∞),s.t.?| y |≥d,g1|y|α≤ |g (y) |≤g2| y |α.

(2) ug(u )＞0,?| u |＞d.

(H 3) ?0＜ε?1,s.t.

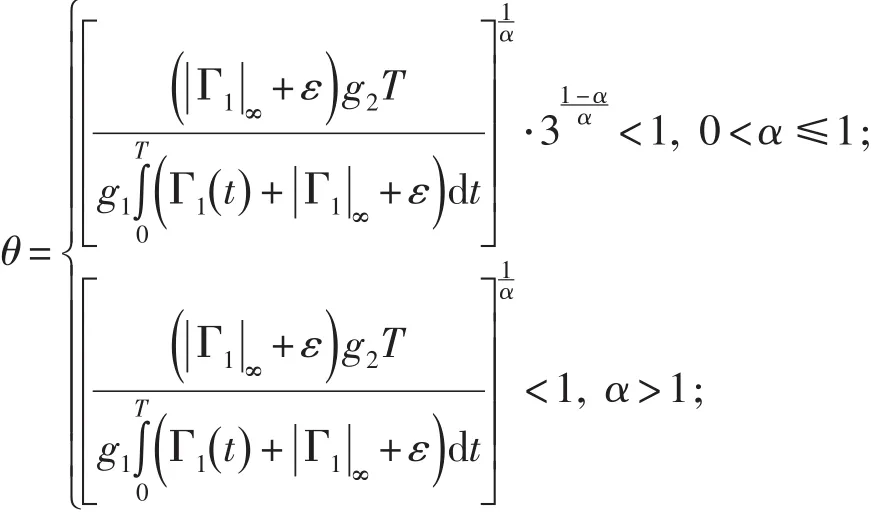
(H 4 )下列條件之一成立：

2） α=p-1,且

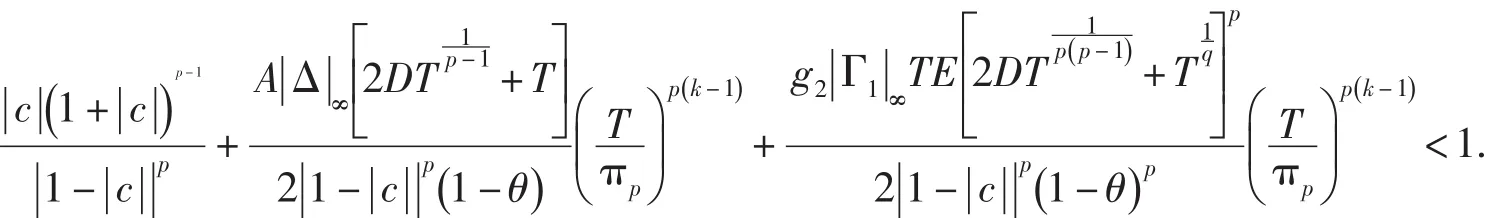
其中

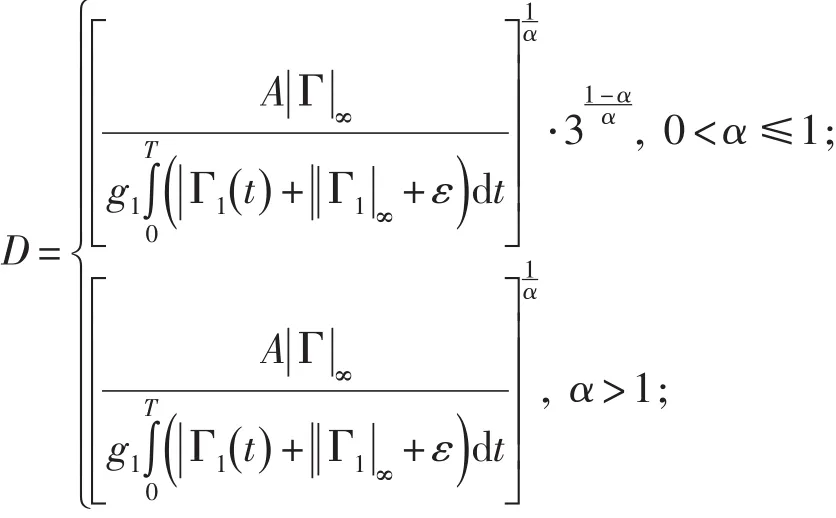
則方程（3）存在一個T-周期解.

證明 顯然，方程（3）有一個T-周期解當且僅當Lx=Nx有一個T-周期解.考察方程Lx=λNx,λ∈(0 ,1).令Ω1={x :Lx=λNx,λ∈(0 ,1)}.若 x∈Ω1，則

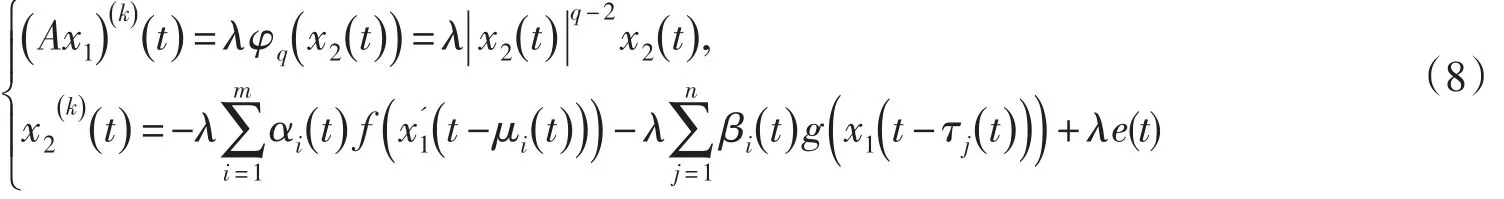
由方程組（8）的第一個方程，得

代入方程組（8）的第二個方程得

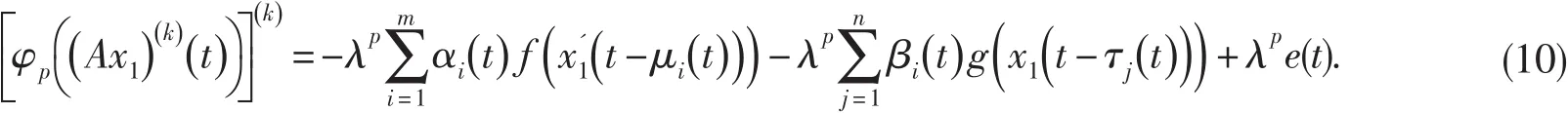
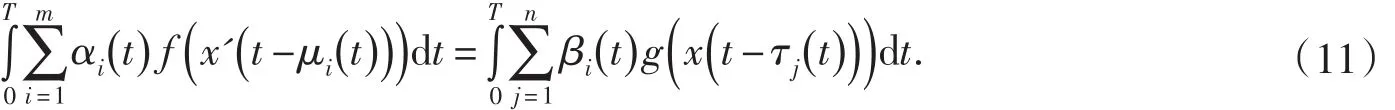
由引理4，

類似可知

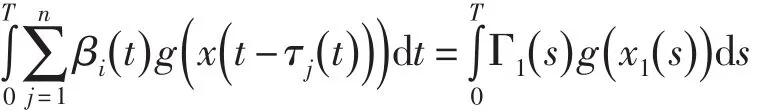
于是，由（11）有

改寫（12）式為

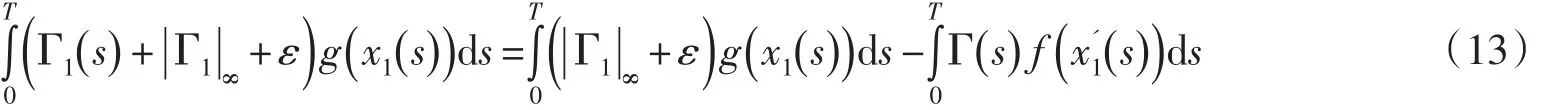
其中0＜ε?1如（H3）所定義.根據積分中值定理，?ξ∈[0,T],s.t.

下證

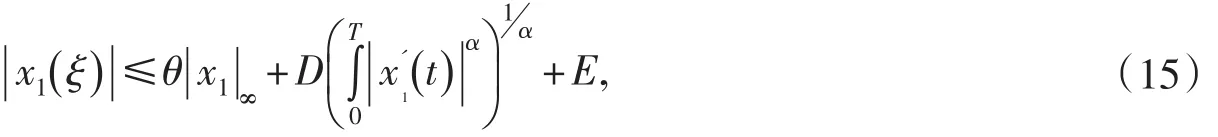
其中常數

若 | x1(ξ)|≤d，則（15）顯然成立.若 | x1(ξ)|＞d，記

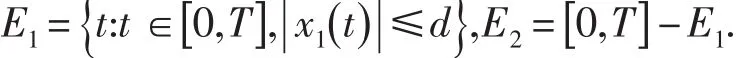
則由（14）得

由條件(H2)容易推出

于是

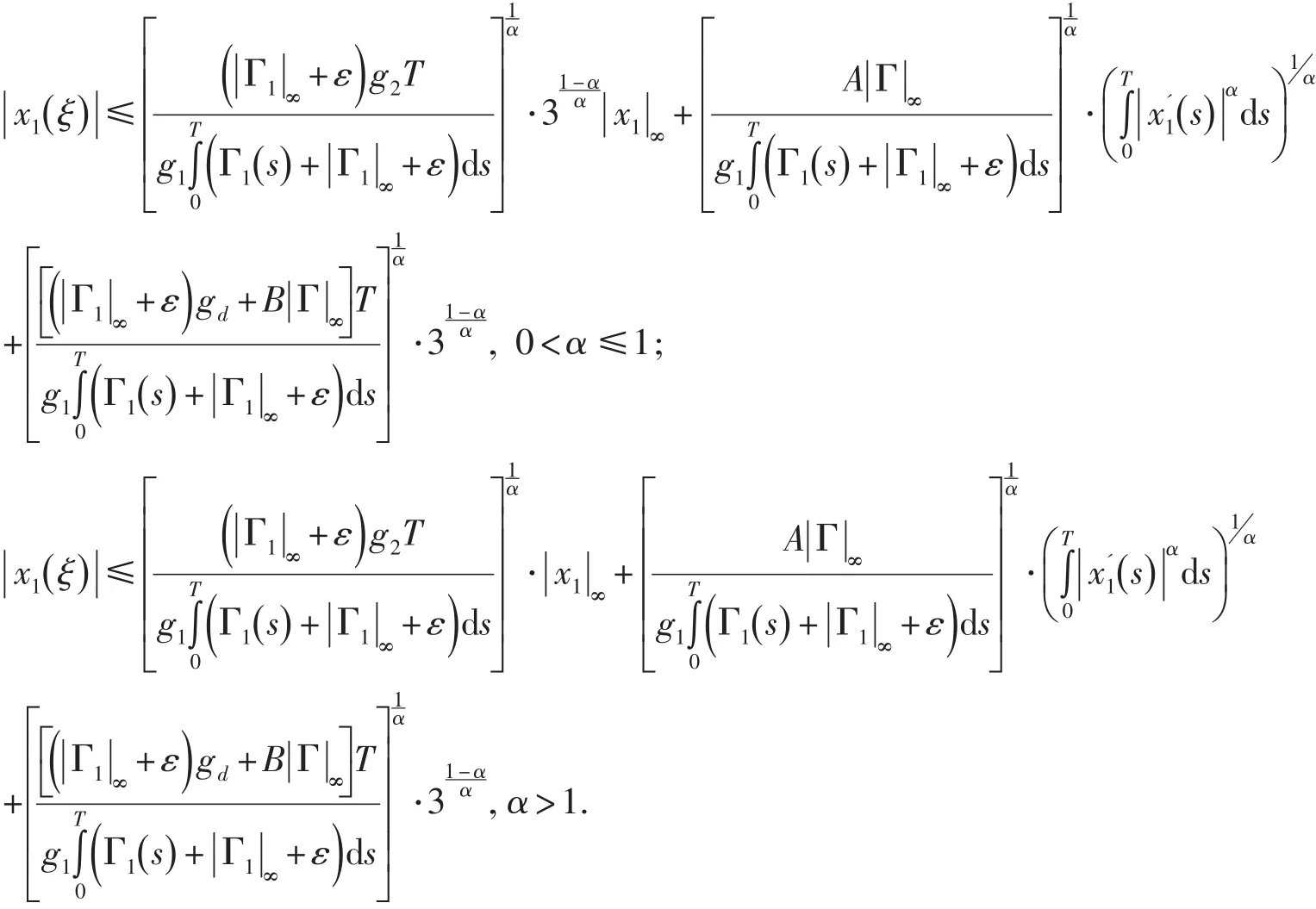
因此（15）成立.再注意到（H2）和引理2

結合(15)可得

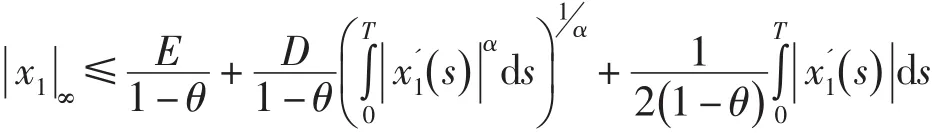
由方程（10）兩邊同乘以x1(t)，并在區間[0 , T]上積分即得

又

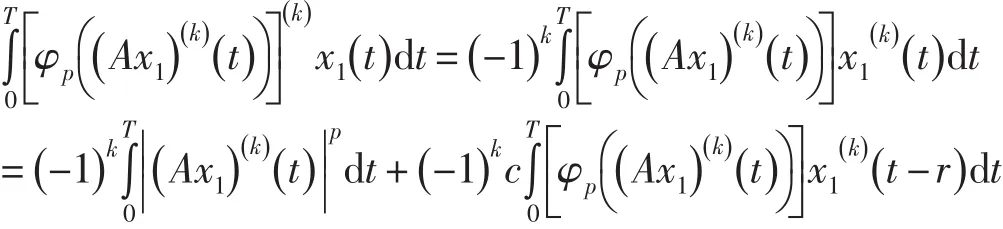
于是，可得

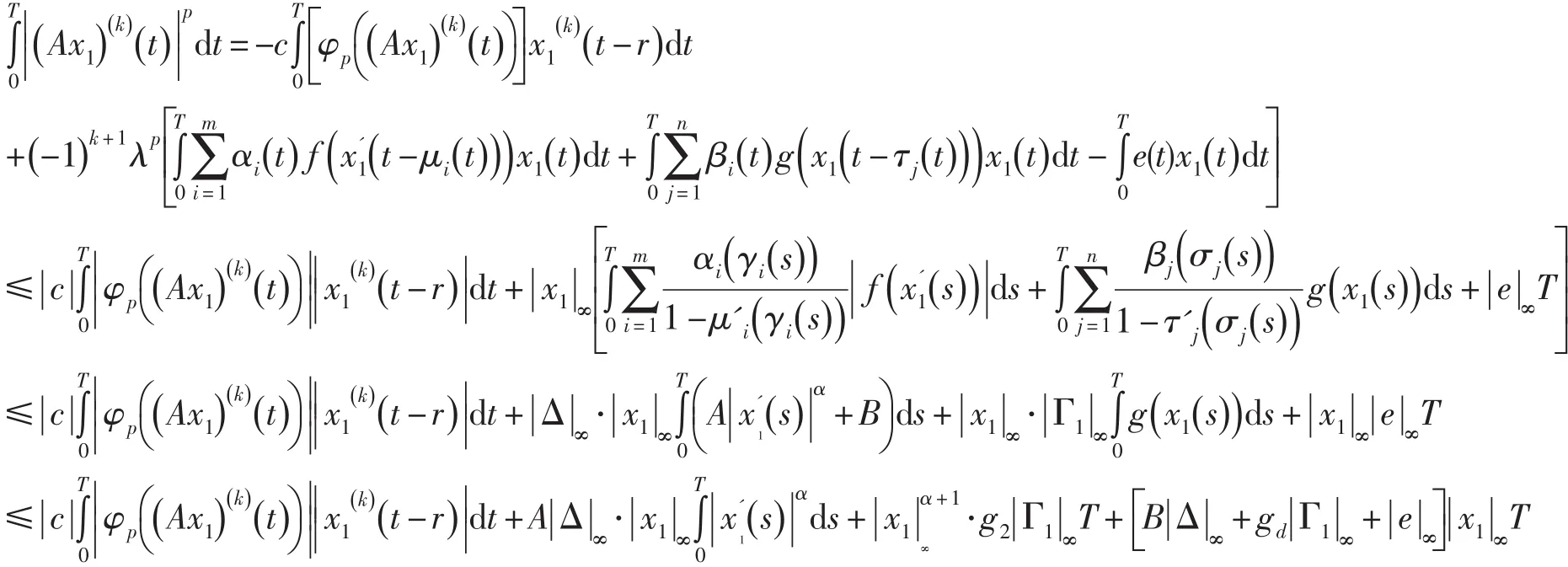
注意到

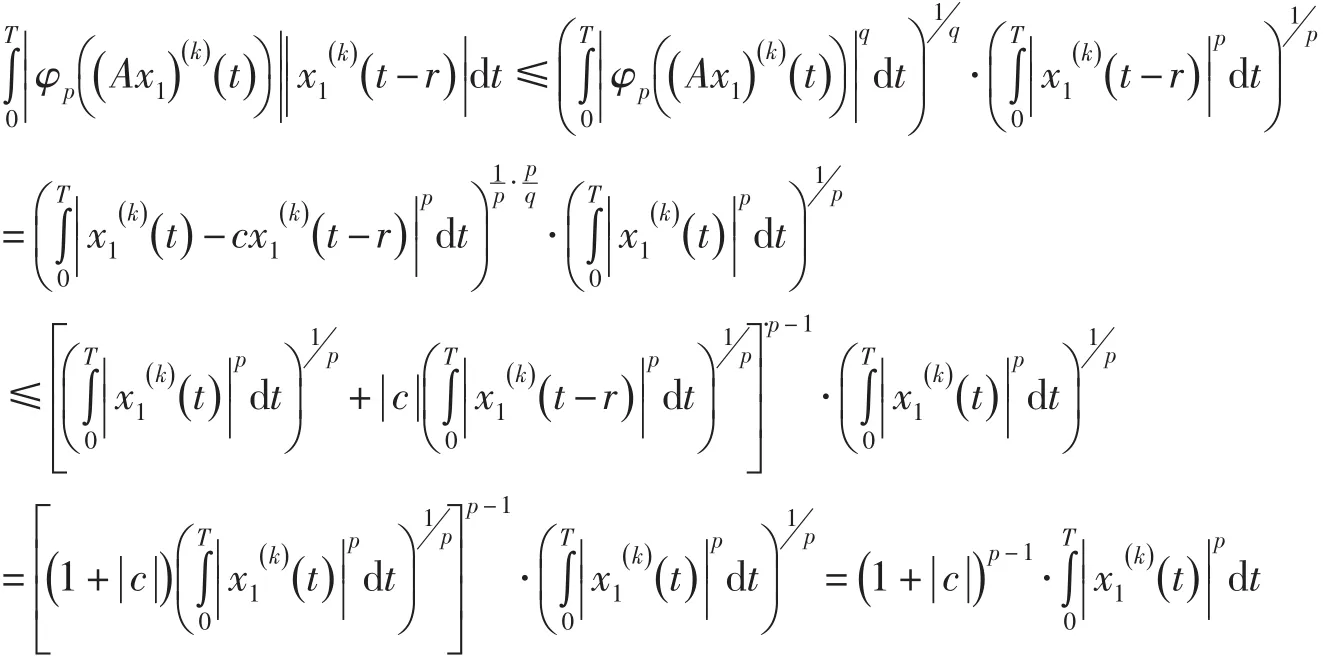
于是，有

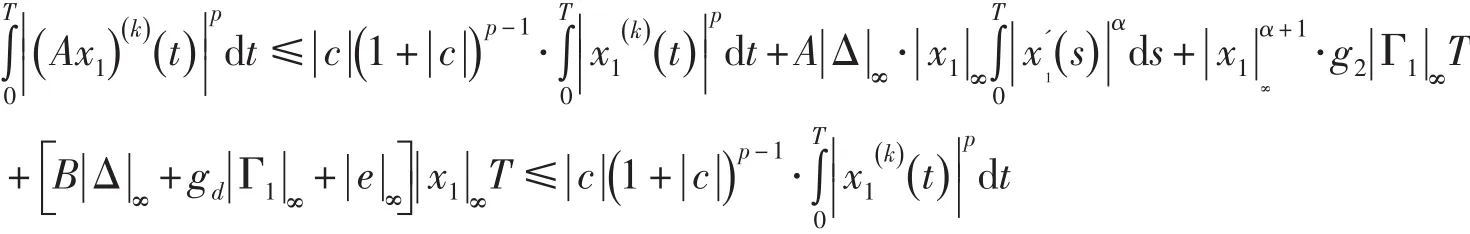
下面分兩種情形討論：

情形I 若α=p-1,且

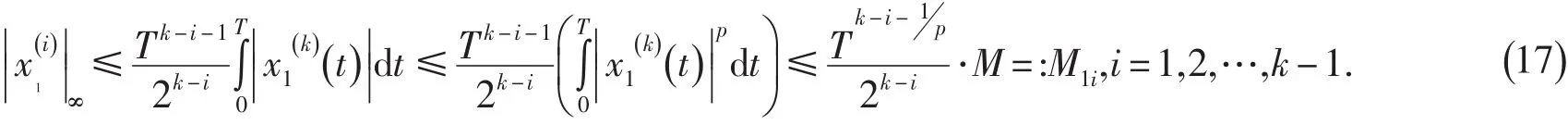
由(16)知存在與λ無關的常數M10＞0.s.t.| x1|∞≤M10.

由方程組（8）的第二個方程，可知

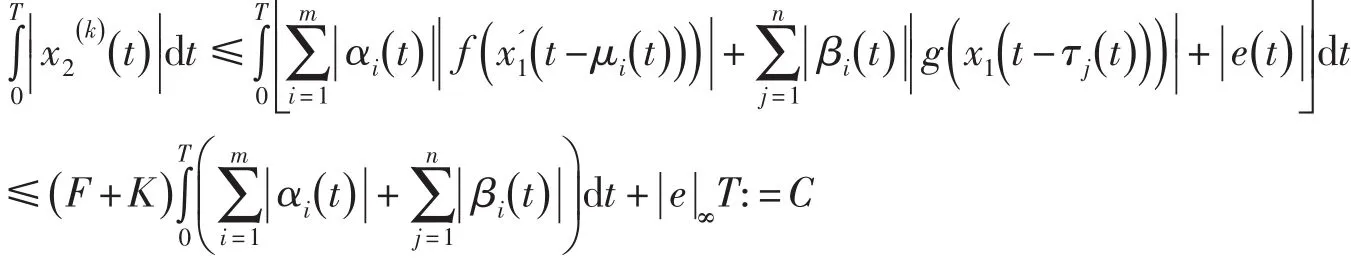
其中K=:max{| g (u)|:u∈[- M10,M10]},F=:max{| f (u)|:u∈[- M11,M11]}.

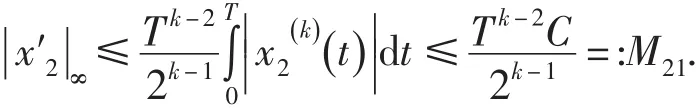
由方程組（8）的第一個方程在[ ]0,T積分得

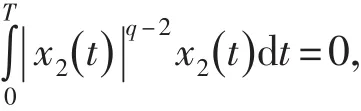
從而?t2∈[0 , T],s.t.x2(t2)=0.故

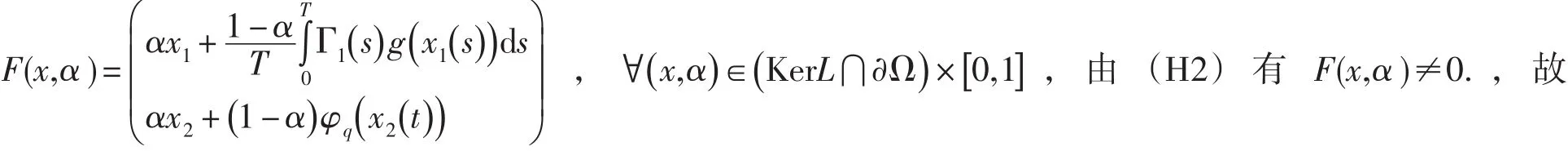
F(x,α)為同倫變換，從而

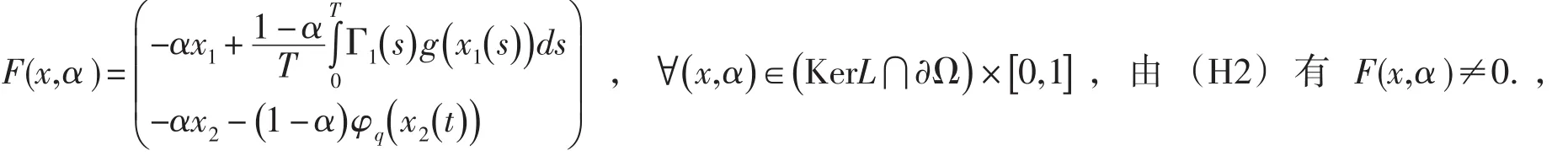
故 F(x,α)為同倫變換，從而

由引理1，方程Lx=Nx在Ωˉ?D(L)中有解.即方程（3）有一個T-周期解x1()t.

3 注記和例子

注記1 定理1中的條件（H2）的（2）換為(2)*ug(u)＜0,?| u |＞d.其余條件不變，結論仍然成立.

注記2 令k=1,可見本文推廣和改進了文獻[5]的結果.

例考慮方程

對應于方程（3），令

由定理1，方程（18）存在一個2π周期解.

[1]LIU Bingwen.Existence and uniquenees of periodic solutions for a kind of Lienard type p-Laplacian equation[J].Nonlinear Analysis，2008，69：724-729.

[2]張志戎，魯世平.一類具偏差變元高階p-Laplace微分方程的周期解[J].吉林大學學報：理學版，2011，49（1）：71-75.

[3]LIJ W，WANG G Q.Sharp inequalities for periodic functions[J].Applied Mathematics E-Notes，2005（5）：75-83.

[4]DU Bo,Huaian,HU Xue,Anqingping.Periodic solutions to a p-Laplacian neutral Rayleigh equation with deviating argument[J].Appl.ofMath,2011，6（3）：253-264.

[5]湯干文，秦發金，羅朝輝，等.具有多個偏差變元的Rayleigh型p-Laplacian泛函微分方程的周期解[J].數學的實踐與認識，2012，42（2）：177-188.

[6]GAINES R E,MAWHIN J L.Coincidence degree and nonlinear differential equations[M].Berlin:Springer-Verlag，1977:95-169.

[7]LU Shiping,GE Weigao.On the existence ofperiodic solutions for neutralfunctionaldifferentialequation[J].Nonlinear Analysis，2003，54：1285-1306.

[8]LU Shiping.On the existence ofpositive periodic solutions for functional differentialequation with deviating arguments[J].J.Math Anal.Appl，2003，280（2）：321-333.