基于GPS測站坐標殘差序列的ARMA建模方法研究*

田 亮 孫付平 李楚陽

(1)解放軍61363部隊，西安 710054 2)解放軍信息工程大學測繪學院，鄭州450000)

基于GPS測站坐標殘差序列的ARMA建模方法研究*

田 亮1)孫付平2)李楚陽1)

(1)解放軍61363部隊，西安 710054 2)解放軍信息工程大學測繪學院，鄭州450000)

以GPS測站坐標殘差序列為實驗對象，采用ARMA模型兩種經典建模方法(Box-Jenkins方法和Pandit-Wu方法)進行了建模擬合的比較與分析。實驗比較發現，當殘差數據比較豐富時兩種建模方法擬合效果理想，無明顯差異，當實驗數據較少時，Pandit-Wu方法擬合效果更好一些，剩余殘差振幅較Box-Jenkins方法減少約，且分布更加平穩。

GPS;坐標殘差;ARMA模型;時間序列分析;ITRF2008

1 引言

隨著各種空間定位技術的迅速發展與成熟，國際地球參考框架的精度和穩定性取得了很大提高［1］。但是為了更加精確地描述地球表面各種毫米量級地球動力學變化，國際大地測量學界又提出了地心坐標精度接近或達到1 mm的新目標。要達到如此高的精度目標，勢必對各種空間技術的觀測精度以及數據處理方法和模型提出了更高的要求。在這樣的背景下國際地球參考框架ITRF2008于2010年成功推出。該地球參考框架無論精度還是穩定性方面都大大優于以往的ITRF系列［2］。但是通過分析ITRF2008測站坐標剩余殘差序列，發現依然包含許多周期性的誤差規律沒有進行模型改正。本文曾對這些尚未模型改正的誤差規律進行了建模擬合研究［3］，發現ARMA建模擬合效果明顯優于三角函數法以及小波分析等擬合方法。因此本文對ARMA模型的不同建模方法做了進一步比較研究，對常用的Box-Jenkins方法和Pandit-Wu方法進行實驗比較與分析。

2 計算方法

ARMA模型定義為［4，5］

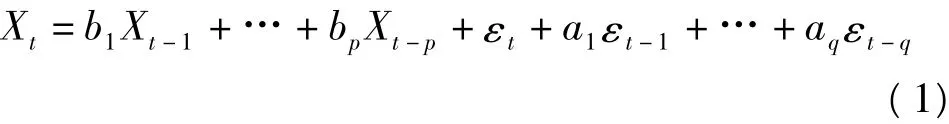
其中{εt}～WN(0，σ2)，p、q≥0為整數，(p，q)為模型的階數，記為{Xt}～ARMA(p，q)。

值得注意的是ARMA模型建模時要求時間序列必須為平穩序列，但在實際測量中，時間序列往往包含一些非平穩的趨勢項和周期項。為此在使用模型擬合前要先提取趨勢項和周期部分或者采用差分方法對時間序列進行預處理，使其滿足平穩性的要求。基于差分后的時間序列所建立的模型又稱為ARIMA模型，記為{Xt}～ARIMA(p，d，q)。

2.1 Box-Jenkins方法建模

經數據預處理后殘差序列采用Box-Jenkins方法建模擬合，主要建模步驟如下:

1)殘差序列平穩性(ADF)檢驗。確定殘差序列是否平穩，如果殘差序列為非平穩序列，則進行差分處理。

2)模型識別。判斷殘差時間序列的自相關和偏自相關函數的形式，如果模型自相關函數拖尾，偏自相關函數截尾，采用AR模型;如果模型自相關函數截尾，偏自相關函數拖尾，采用MA模型;如果兩者皆拖尾，采用ARMA模型。

3)模型定階采用AIC最小信息準則。

4)模型參數估計采用非線性最小二乘估計方法。

5)模型的適應性檢驗，即檢驗剩余殘差是否為白噪聲序列。

2.2 Pandit-Wu方法建模

具體建模步驟如下:

1)ADF檢驗。確定殘差序列是否平穩，如果檢驗殘差序列為非平穩序列，將進行差分處理。

2)從n=1開始，逐漸增加模型階數，擬合ARMA(2n，2n-1)模型，依次為ARMA(2，1)、ARMA (4，3)、ARMA(6，5)…即以兩階為單位逐漸增加模型階數，直到F檢驗表明當再增加模型階數時，剩余殘差平方和不再顯著減小為止。如果系統的確是階數為奇數的模型，那么擬合的較高階數為偶數的模型第2n個自回歸系數的絕對值必然接近于零。那么我們可以刪除這樣的小參數得到較低奇數階的模型。

3)模型適應性檢驗。

4)求最優模型。采用F檢驗判斷模型是否包含小參數，若有參數可以刪除，擬合較低階的模型，從而得到最優模型。

3 算例分析

3.1 數據選取

選取的實驗數據為ITRF2008解的衍生產品GPS測站坐標殘差序列［6-8］，絕大部分GPS坐標殘差序列包含了1997—2009年約12年的殘差數據，采樣間隔為7天，部分殘差序列存在間斷點或粗差。因此首先對選取的殘差序列進行數據預處理，對于含有間斷點的殘差序列進行插值擬合，存在粗差的情況，設定閾值(通過殘差文件中給出的formal error來判斷)進行剔除。

3.2 實驗結果比較與分析

由于全球GPS測站坐標殘差序列數據量非常大，受篇幅限制本文僅選取部分測站作為實驗對象，HOFN測站(64°N，164°W)數據累積豐富且觀測數據質量較高，沒有明顯的外部因素突發性影響，因此以HOFN測站坐標殘差序列為實驗對象非常理想。

首先利用Box-Jenkins方法對HOFN測站坐標殘差序列進行建模擬合，定階準則采用AIC信息準則，階數選取如表1所示，實際建模效果如圖1～3所示。

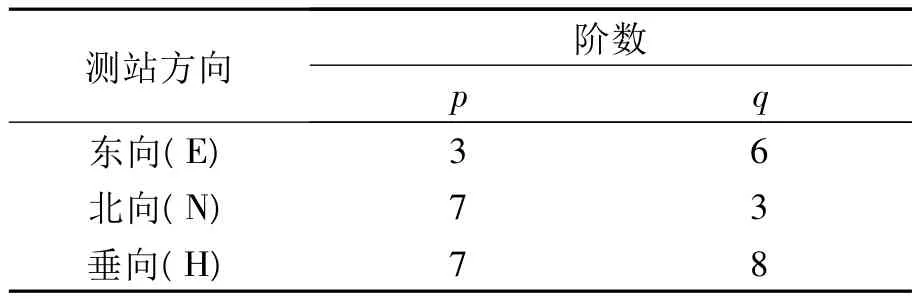
表1 ARMA模型(Box-Jenkins方法)階數選取Tab.1 Selection of the order number with ARMA model (Box-Jenkins)

利用Pandit-Wu方法建模階數選取如表2所示，實際建模效果如圖4～6所示。

通過觀察擬合圖和剩余殘差圖可以發現，兩種建模方法的擬合效果都比較理想，沒有顯著差異。細微來看Pandit-Wu方法擬合后剩余殘差振幅比Box-Jenkins方法稍小，但是效果不明顯。為了進一步區分比較兩種方法，對上述實驗進行改動，實驗數據截取一半即選取HOFN測站殘差序列5年的殘差數據(1997—2001年的時間序列)作為實驗對象，采用上述兩種方法進行建模擬合比較。擬合效果如圖7～9所示。

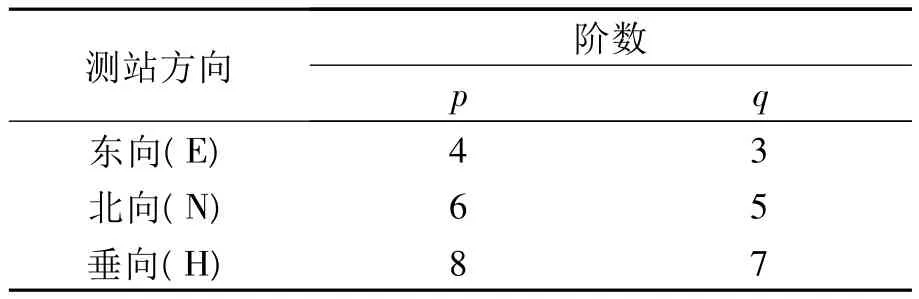
表2 ARMA模型(Pandit-Wu方法)階數選取Tab.2 Selection of the order number of ARMA model (Pandit-Wu)

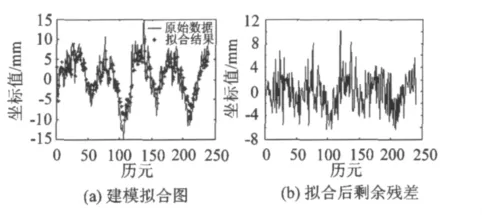
圖1 垂向擬合結果Fig.1 Vertical fitting results with Box-Jenkins method

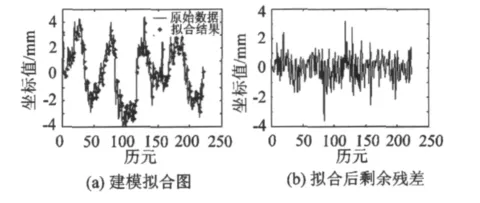
圖2 東向擬合結果Fig.2 Eastward fitting results with Box-Jenkins method

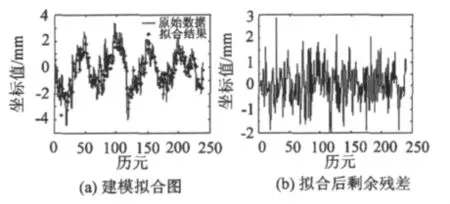
圖3 北向擬合結果Fig.3 Northward fitting results with Box-Jenkins method

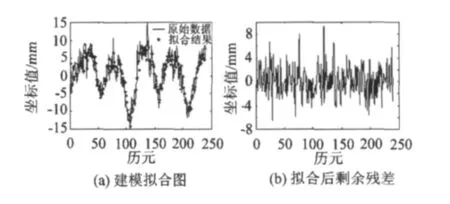
圖4 垂向擬合結果Fig.4 Vertical fitting results with Pandit-Wu method

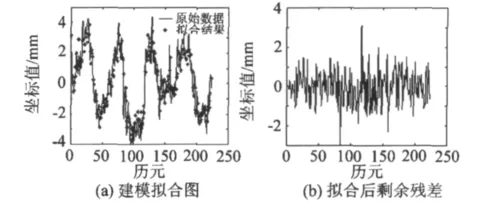
圖5 東向擬合結果Fig.5 Eastward fitting results with Pandit-Wu method

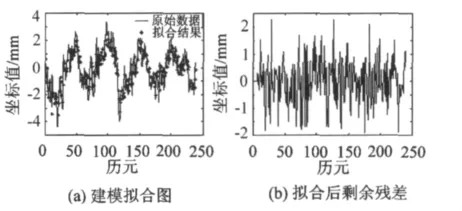
圖6 北向擬合結果Fig.6 Northward fitting results with Pandit-Wu method

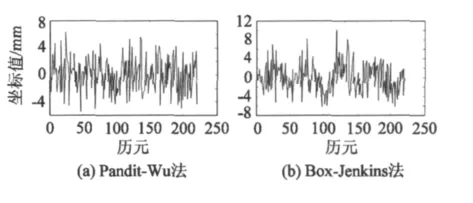
圖7 垂向擬合剩余殘差比較Fig.7 Comparison between the residuals after vertical fitting with the two methods

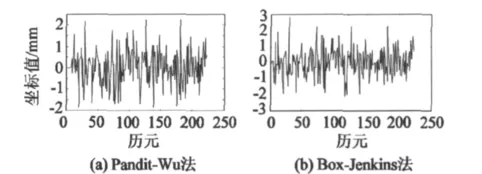
圖8 北向擬合剩余殘差比較Fig.8 Comparison between residuals after northward fitting with the two methods

通過3個方向的剩余殘差圖比較可以發現，兩種建模方法在實驗數據減少一半的情況下擬合結果出現了較大差別:Pandit-Wu方法擬合后垂向剩余殘差振幅在 6 mm左右，Box-Jenkins方法達到了10mm;Pandit-Wu方法擬合后殘差分布仍然無明顯周期性振動規律，而Box-Jenkins方法擬合剩余殘差明顯存在一定的周期性振動規律。東向和北向剩余殘差經Pandit-Wu方法擬合后振幅在2mm左右，Box-Jenkins方法達到了3 mm。由此可見Pandit-Wu方法的擬合效果優于Box-Jenkins方法。

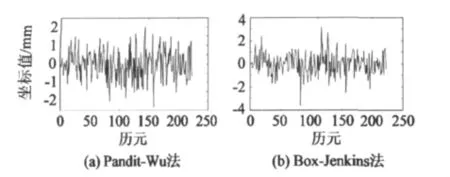
圖9 東向擬合剩余殘差比較Fig.9 Comparison between residuals after eastward fitting with the two methods

之所以Pandit-Wu方法擬合效果更加理想，從原理上分析主要是因為Box-Jenkins建模方法是以時間序列的自相關函數和偏自相關函數的統計特性為依據，但是在建模之前我們并不知道時間序列的理論自相關函數，而是用樣本自相關函數和偏自相關函數來近似，因此不可避免地會產生誤差。尤其是當采樣數據較少時，樣本無法完全代表總體殘差分布，誤差將不可避免。而Pandit-Wu方法無需了解殘差序列特性，只需要逐漸增加模型階數，直到剩余殘差平方和不再顯著減小為止。可見在無法預知樣本內部信息的前提下，Pandit-Wu方法更加方便可靠。

5 結束語

通過對GPS測站坐標殘差序列采用ARMA兩種經典建模方法進行建模比較發現，Pandit-Wu方法的建模效果無論是在數據豐富還是缺乏時都能保持得很好，采用該法對剩余殘差序列進行建模擬合對于進一步提高測站地心坐標精度，提高國際地球參考框架的精度和穩定性有重要意義。

1 陳俊勇.大地坐標框架理論和實踐的進展［J］.大地測量與地球動力學，2007，(1):1-6.(Chen Junyong.Progress in theory and practice for geodetic reference coordinate frame［J］.Journal of Geodesy and Geodynamics，2007，(1):1-6)

2 黃立人.地殼運動的參考框架［J］.大地測量與地球動力學，2002，(3):102-108.(Huang Liren.The reference frame of earth deformation［J］.Journal of Geodesy and Geodynamics，2002，(3):102-108)

3 田亮，等.GPS測站坐標非線性變化研究方法的比較與分析［J］.測繪工程，2011，20(2):27-29.(Tian Liang，et al.Comparative analysis of studying on GPS station non-linear variation［J］.Engineering of Surveying and Mapping，2011，20(2):27-29)

4 王振龍，胡永宏.應用時間序列分析［M］.北京:科學出版社，2007.(Wang Zhenlong and Hu Yonghong.The application of time series analysis［M］.Beijing:Science Press， 2007)

5 陳杰.MATLAB寶典［M］.北京:電子工業出版社，2006.(Chen Jie.MATLAB canon［M］.Beijing:Electronics Industry Press，2006)

6 http://itrf.ensg.ign.fr/ITRF_solutions/2008/ITRF2008.php，2010.

7 http://itrf.ensg.ign.fr/ITRF_solutions/2008/doc/ ITRF2008_GPS.SSC.txt，2010.

8 Dennis D and McCarthy D D(eds.).IERS Conventions (2003)，IERS Technical Note No.32，2003.

STUDY ON ARMA MODEL BASED ON GPS STATION COORDINATE RESIDUAL SERIES

Tian Liang1)，Sun Fuping2)and Li Chuyang1)

(1)61363 Troops of PLA，Xi’an 710054 2)PLA Information Engineering University，Zhengzhou 450000)

As to GPS station coordinate residuals，we used two classical ARMA modeling methods(Box-Jenkins method and Pandit-Wu method)to fit the GPS station coordinate residuals，and made comparative study.According to the experiment，we found out that the two methods have a little difference while there is abundant data.If the data is poor，with the Pandit-Wu method the results will be better.The amplitude of residuals reduces aboutand the distribution is more uniform.

GPS;coordinate residuals;ARMA model;time series analysis;ITRF2008

1671-5942(2012)02-0124-04

2011-11-30

國家自然科學基金(41074011)

田亮，1987年生，工學碩士，助理工程師，主要研究方向為空間大地測量.E-mail:tl200431610237@126.com

P207

A