二進制本原BCH碼的參數(shù)盲識別

王蘭勛，李丹芳，汪洋

（河北大學 電子信息工程學院，河北 保定 071002）

二進制本原BCH碼的參數(shù)盲識別

王蘭勛，李丹芳，汪洋

（河北大學 電子信息工程學院，河北 保定 071002）

針對BCH碼的盲識別問題，提出一種基于歐幾里德算法的最大公因式的識別方法．首先，根據(jù)循環(huán)移位碼字求取最大公因式，得到最大公因式的系數(shù)矩陣．然后，分析最大公因式的次數(shù)分布規(guī)律確定碼長，由系數(shù)矩陣求出生成多項式．該識別方法簡單易行，無繁雜的矩陣運算．理論分析及仿真實驗表明，無誤碼時使用較小的數(shù)據(jù)量就可有效識別；誤碼率為10－2，數(shù)據(jù)量足夠時，識別效果仍然較好．

BCH碼；歐幾里德算法；最大公因式；盲識別

信道編碼盲識別是一個全新的領(lǐng)域，其主要應用在信息對抗、協(xié)作通信以及自適應調(diào)制編碼技術(shù)（AMC）等領(lǐng)域．據(jù)現(xiàn)在公開發(fā)表的文獻來看，大部分文獻集中在卷積碼的盲識別上，較少研究線性分組碼的盲識別．文獻［1］建立了一種線性分組碼的識別模型，是在無誤碼條件下的全盲識別，但其分析所需數(shù)據(jù)量會隨碼長估值的擴大急劇增大，導致其實用意義不大．文獻［2］則對該方法做了一定的改進，大大減少了樣本數(shù)據(jù)量，提高了實用性，并將其應用于工程實踐中．文獻［3］根據(jù)碼重分布估計碼長，進而通過矩陣化簡得出生成矩陣，該算法對低碼率二進制線性分組碼有較好的識別效果．文獻［4］在文獻［3］的基礎(chǔ)上先識別出碼長，再根據(jù)碼字與校驗矩陣的校驗關(guān)系識別出生成多項式．文獻［5］用經(jīng)典的BM算法求解循環(huán)碼的盲識別模型，算法較復雜．文獻［6］采用秩統(tǒng)計的方法識別出碼長，再用統(tǒng)計的方法獲取生成多項式的根，進而得到生成多項式，識別繁瑣，計算量較大．文獻［7］根據(jù)碼根信息差熵識別碼長，并采用碼根統(tǒng)計的方法識別生成多項式，同樣所需數(shù)據(jù)量較大．

本文針對本原BCH碼的特殊性質(zhì)，結(jié)合歐幾里德算法，提出一種新的識別方法．該方法識別原理簡單，并具有較好的容錯性，經(jīng)實驗驗證在無誤碼較少的數(shù)據(jù)量時可達到識別的目的，有誤碼數(shù)據(jù)量足夠時，仍有較好的識別效果．

1 BCH碼識別基礎(chǔ)

定義1［8］給定任一有限域GF（q）及其擴域GF（qm），其中q是素數(shù)或素數(shù)的冪，m為某一正整數(shù)．若碼元取自GF（q）上的一個循環(huán)碼，它的生成多項式g（x）的根集合R中含有以下δ－1個連續(xù)根：

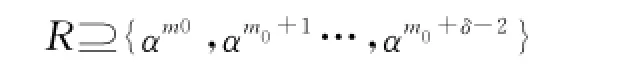
時，即則由g（x）生成的循環(huán)碼稱為q進制BCH碼．通常取m0＝1，如果生成多項式g（x）的根中，有一個GF（2m）中的本原域元素，則n＝qm－1，當q＝2時，稱這種碼長n＝2m－1的BCH碼為二進制本原BCH碼．

二進制本原BCH碼具有的性質(zhì)：

1）循環(huán)性．循環(huán)性是指任一碼組循環(huán)移位以后，仍為該碼中的一個碼組．

2）所有碼多項式T（x）都是g（x）的倍式．可寫成

本文所用歐幾里德算法是用于搜尋二元域上的多項式c（x）和c′（x）的最大公因式d（x），即方程

如何找到d（x）是本文研究的重點．

定理1 設(shè)c（x）和c′（x）是二元域上的2個多項式，則有唯一的一對二元域上的多項式q（x）和r（x），具有下面的性質(zhì)：

其中r（x）的次數(shù)小于c′（x）的次數(shù)，叫余式．

該定理也叫做歐幾里德除法定理．其中q（x）就是除法中的商式，r（x）是c（x）除以c′（x）所剩的余式，定義（c（x），c′（x））為c（x）和c′（x）的最大公因式．經(jīng)典的歐幾里德算法即不斷利用定理1作除法可得下列：

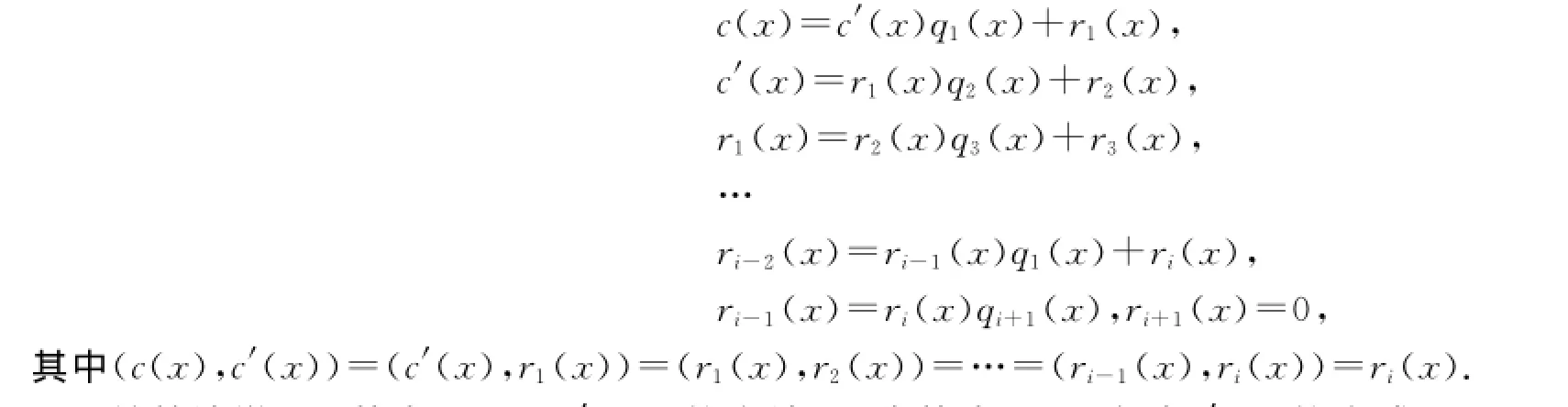
該算法說明了找出（c（x），c′（x））的方法，即先找出c（x）除以c′（x）的余式r1（x），再找出c′（x）除以r1（x）的余式r2（x），依此類推找出rj－1（x）與rj（x）的余式rj＋1（x），直到余式為0．因為以上多項式均是二元域上的多項式，所以式中的運算均為模二運算．BCH碼多項式的歐幾里德算法可以用輾轉(zhuǎn)相除的方法來實現(xiàn)［9］．

當截獲碼流后，根據(jù)幀同步的信息很容易確定BCH碼的起始點，所以本文的識別研究是在起始點已知的條件下進行的，這也是符合實際情況的．

2 識別方法

本文提出的識別方法是利用歐幾里德算法計算循環(huán)移位前后2個碼字多項式的最大公因式d（x）．因為循環(huán)碼的每個碼字均是生成多項式的倍式，所以它們的最大公因式是生成多項式或生成多項式的倍式，由仿真實驗分析得出碼長n和生成多項式g（x）．下面對該方法進行詳細描述．

2．1 數(shù)學公式描述

BCH碼的編碼數(shù)學模型為

其中c（x）為碼字多項式，m（x）為信息多項式，g（x）為生成多項式．實際應用中，c（x）為接收或截獲的碼流，在不知道任何編碼參數(shù)的情況下通過識別方法獲得g（x），進而得到該碼流攜帶的信息m（x）．

2．2 基于歐幾里德算法的識別原理

因任一BCH碼多項式c（x）都是g（x）的倍式，所以同一碼組中2個BCH碼多項式的最大公因式不是g（x）就是g（x）的倍式．而若假設(shè)c（x）是BCH碼的一個碼組，所以c（x）循環(huán)移位m次的結(jié)果c′（x）也必為該碼中的一個碼組．根據(jù)這一性質(zhì)結(jié)合歐幾里德算法計算出最大公因式d（x），進而通過數(shù)據(jù)分析得到g（x）．

首先，截獲一段BCH碼碼流，遍歷m，對于二進制BCH碼m通常取3到8．然后，由n＝2m－1對碼流分組，得到碼字矩陣，將碼字矩陣循環(huán)移位m次，運用文中介紹的歐幾里德算法計算循環(huán)移位前后碼字的最大公因式d（x），得到最大公因式的系數(shù)矩陣，進而求出d（x）的次數(shù)?0（d（x）），用matlab仿真?0（d（x））的分布圖．若m選取正確，即n正確，d（x）的次數(shù)大部分大于某一數(shù)值，即次數(shù)閾值．這個閾值就是生成多項式的次數(shù)，因為最大公因式不是g（x）就是g（x）的倍式，所以大部分?0（d（x））是大于或等于?0（g（x））的；若m選取錯誤，d（x）的次數(shù)分布無此規(guī)律，大小不均．在m選取正確時，獲取碼長n，得到d（x）的系數(shù)矩陣，并記錄次數(shù)閾值，以及該閾值對應的最大公因式，分解這個公因式，具有連續(xù)根的因子就是生成多項式g（x）．至此，完成識別．

綜上所述，二進制本原BCH碼的識別流程如圖1所示．

圖1 BCH碼識別流程Fig．1 Recognition flow of BCH codes

3 仿真驗證及分析

采用上述識別方法，分別在無誤碼和有誤碼的情況下進行實驗仿真．本文以（15，5）的二進制本原BCH碼為例．

3．1 無誤碼識別

在無誤碼的條件下，獲取一定數(shù)據(jù)量的碼流，遍歷m＝3～8，采用歐幾里德算法計算BCH碼字與循環(huán)移位m次的碼字的最大公因式，如碼字c＝［010011011100001］，向右循環(huán)移四位得c′＝［000101001101110］，通過輾轉(zhuǎn)相除的方法實現(xiàn)歐幾里德算法，得最大公因式d（x）＝r6（x），如圖2所示．用matlab編程實現(xiàn)歐幾里德算法并仿真d（x）的次數(shù)分布，得圖3和圖4分別是當m＝3和m＝4時取100組碼字進行實驗的仿真圖．由圖3和圖4比較可明顯看出當m＝3時，最大公因式的次數(shù)分布無規(guī)律性，在0，1，2，3，4，5均有分布；而m＝4時，最大公因式的次數(shù)100%在10以上，且分布在10和11的居多，有明顯的規(guī)律性，10即為次數(shù)閾值，則碼長n＝24－1＝15．截取部分最大公因式的系數(shù)矩陣如圖5所示，d（x）次數(shù)為從序列最右邊第1個1數(shù)到最左邊1所在的位置，從0開始計數(shù)．選取次數(shù)最小的最大公因式10100110111進行因式分解，取有連續(xù)根的因式，得，與題設(shè)相符，識別正確．

圖2d（x）計算Fig．2d（x）algorithm

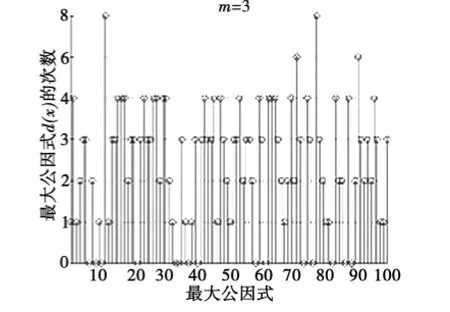
圖3m＝3時100組最大公因式的次數(shù)分布Fig．3 Times distribution of the greatest common factors of 100 groups whenm＝3

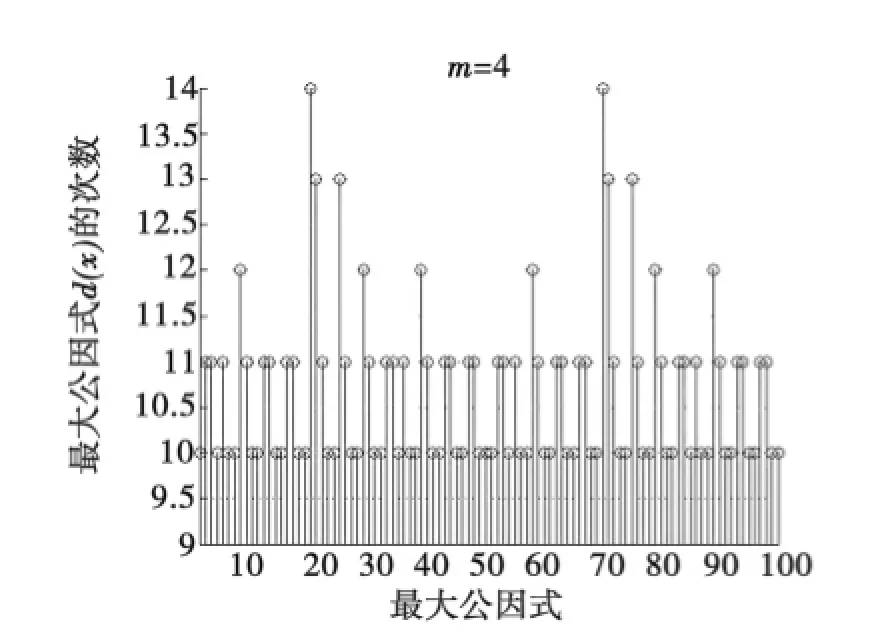
圖4m＝4時100組最大公因式的次數(shù)分布Fig．4 Times distribution of the greatest common factors of 100 groups whenm＝4

圖5 前20組最大公因式的系數(shù)矩陣Fig．5 Top 20 coefficient matrix of the greatest common factors

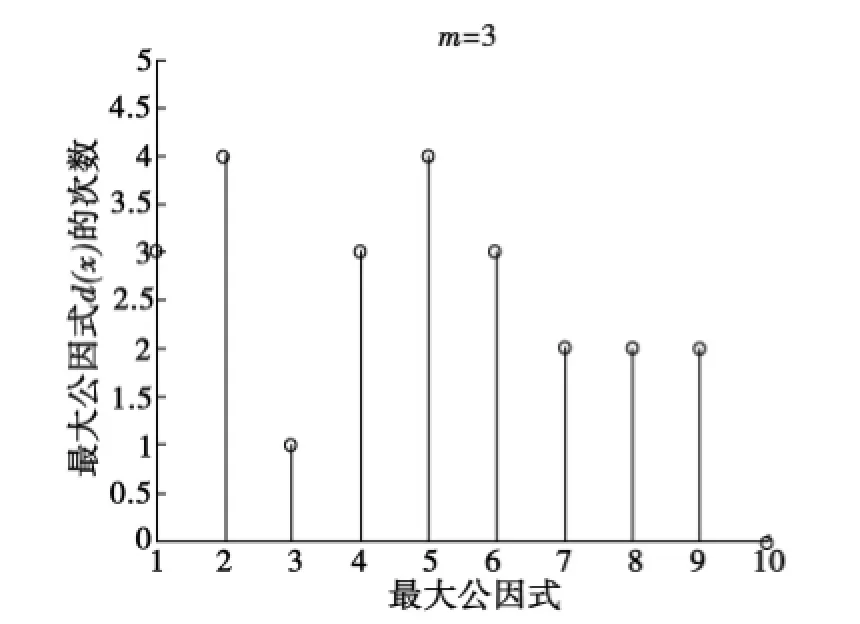
圖6m＝3時10組最大公因式的次數(shù)分布Fig．6 Times distribution of the greatest common factors of 10 groups whenm＝3

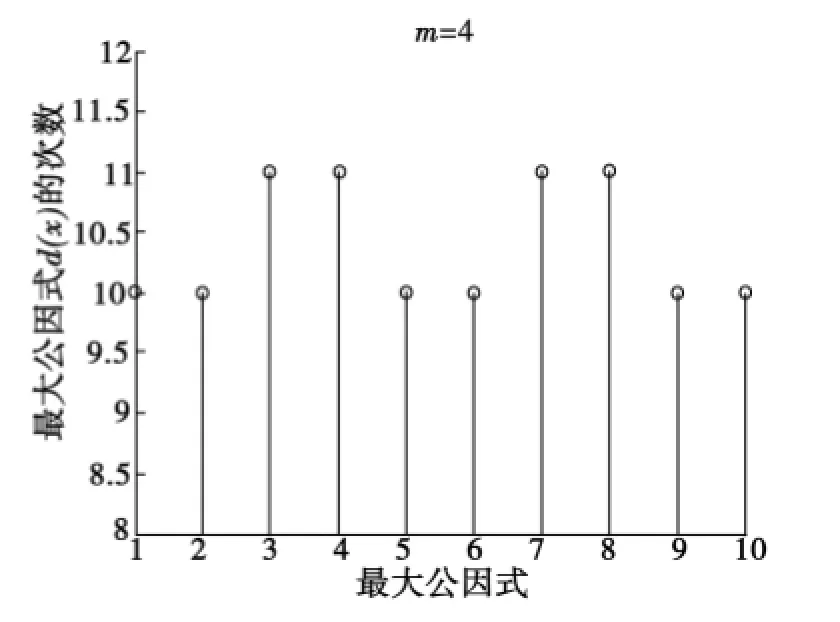
圖7m＝4時10組最大公因式的次數(shù)分布Fig．7 Times distribution of the greatest common factors of 10 groups whenm＝4

取10組碼字仿真驗證，圖6和圖7分別為m＝3和m＝4時最大公因式的次數(shù)分布圖．由圖6和圖7比較，用同樣的方法分析，也可看出m＝4時最大公因式的次數(shù)分布均在10以上，取次數(shù)為10的最大公因式也可求出g（x）；而m＝3時次數(shù)在0，1，2，3，4均有分布，不滿足規(guī)律性．所以在較少的數(shù)據(jù)量時本文的識別方法也有效．

3．2 有誤碼識別

信道誤碼率分別為1×10－3和1×10－2時，取100個碼組的數(shù)據(jù)量．遍歷m＝3～8進行仿真，得m＝4時公因式的次數(shù)分布分別為圖8和圖9（m＝3，5，6，7，8略）．

由圖8可見，在誤碼率為1×10－3時最大公因式的次數(shù)98%均在10以上，且大部分分布在10和11，通過d（x）的系數(shù)矩陣取出次數(shù)為10的最大公因式，經(jīng)驗證其因子有連續(xù)根，為所求生成多項式；由圖9可見，在誤碼率為1×10－2時最大公因式的次數(shù)81%均在10以上，且大部分分布在10和11，同樣的方法得到生成多項式．若取出的10次多項式不能分解出有連續(xù)根的因子，則進行多次選取，保證識別的正確率，所以在較高的誤碼率下該識別方法可達到正確識別的目的．

圖8m＝4，pe＝1×10－3時100組最大公因式的次數(shù)分布Fig．8 Times distribution of the greatest common factors of 100 groups of whenm＝4 whenpe＝1×10－3

對比無誤碼和有誤碼的識別仿真圖，根據(jù)理論分析可知，在無誤碼的條件下，當m選取正確時，移位前后所求最大公因式的次數(shù)均大于等于生成多項式的次數(shù)；當選取的m對應最大公因式次數(shù)為零時說明移位前后碼字互素，不滿足BCH碼的性質(zhì)，與碼長n直接相關(guān)的參數(shù)m選取的不正確，舍棄該m值．這一結(jié)論簡化了無誤碼條件下的BCH碼的盲識別；在有誤碼時，則需根據(jù)最大公因式的次數(shù)分布規(guī)律，分析是否存在次數(shù)閾值來判斷該m值選取的正確性，若存在次數(shù)閾值，m選取正確，反之，不正確．

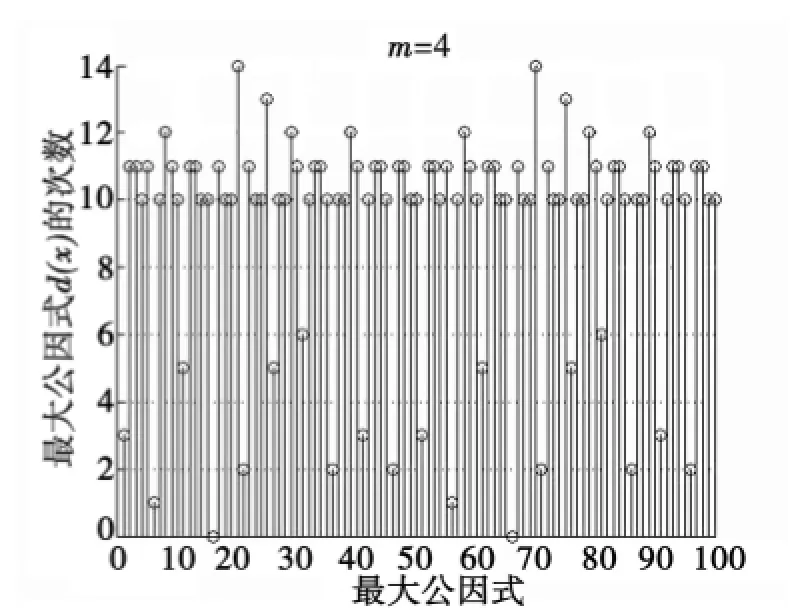
圖9m＝4，pe＝1×10－2時100組最大公因式的次數(shù)分布Fig．9 Times distribution of the greatest common factors of 100 groups ofmwhenpe＝1×10－2

4 結(jié)論

本文對二進制本原BCH碼參數(shù)盲識別提出了一種方法，該方法是基于歐幾里德算法，求取最大公因式系數(shù)矩陣，并分析最大公因式的次數(shù)分布規(guī)律，進而識別出本原BCH碼的碼長和生成多項式．此盲識別算法，識別原理簡單易行，避免了繁雜的矩陣運算，識別過程簡單．仿真實驗結(jié)果表明，在無誤碼時用較少的數(shù)據(jù)量就可達到識別的目的，在誤碼率為pe＝1×10－2時也具有較好的識別效果．

［1］ 薛國慶．卷積碼的盲識別研究［D］．合肥：中國科學技術(shù)大學，2009．

XUE Guoqing．Blind identification of convolutional codes［D］．Hefei：University of Science and Technology of China，2009．

［2］ 陳金杰，楊俊安．無線數(shù)傳信號編碼盲識別與解碼技術(shù)研究［J］．電子測量與儀器學報，2011，25（10）：905－910．

CHEN Jinjie，YANG Junan．Research on blind recognition for wireless digital transmission signals encoding and decoding technology［J］．Journal of Electronic Measurement and Instrument，2011，25（10）：905－910．

［3］ 昝俊軍，李艷斌．低碼率二進制線性分組碼的盲識別［J］．無線電工程，2009，39（1）：19－24．

ZAN Junjun，LI Yanbin．Blind recognition of low code rate binary linear block codes［J］．Radio Engineering，2009，39（1）：19－24．

［4］ 閆郁翰．循環(huán)碼的盲識別［J］．電子科技，2011，24（3）：112－114．

YAN Yuhan．Blind recognition method for the cyclic code［J］．Electronic Science and Technology，2011，24（3）：112－114．

［5］ 劉菁．卷積碼和循環(huán)碼識別技術(shù)研究［D］．西安：西安電子科技大學，2010．

LIU Jing．Research on recognition technology for convolutional codes and cyclic codes［D］．Xi'an：Xidian University，2010．

［6］ 聞年成，楊曉靜．采用秩統(tǒng)計和碼根特征的二進制循環(huán)碼盲識別方法［J］．電子信息對抗技術(shù)，2010，25（6）：26－29．

WEN Niancheng，YANG Xiaojing．Blind recognition of cyclic codes based on rank statistic and codes roots characteristic［J］．E－lectronic Information Warfare Technology，2010，25（6）：26－29．

［7］ 楊曉靜，聞年成．基于碼根信息差熵和碼根統(tǒng)計BCH碼識別方法［J］．探測與控制學報，2010，32（3）：69－73．

YANG Xiaojing，WEN Niancheng．Recognition method of BCH codes based on roots information dispersion entropy and roots statistic［J］．Journal of Detection，2010，32（3）：69－73．

［8］ 王新梅．糾錯碼－原理與方法［M］．西安：西安電子科技大學出版社，2002．

WANG Xinmei．Error correcting code－principles and methods［M］．Xi'an：Xidian University Press，2002．

［9］ 戚林，郝士琦，王磊，等．一種RS碼快速盲識別方法［J］．電路與系統(tǒng)學報，2011，16（2）：70－76．

QI Lin，HAO Shiqi，WANG Lei，et al．A fast blind recognition method of RS codes［J］．Journal of Circuits and Systems，2011，16（2）：70－76．

（責任編輯：孟素蘭）

Blind recognition of binary primitive BCH codes parameters

WANG Lan－xun，LI Dan－fang，WANG Yang
（College of Electronic and Informational Engineering，Hebei University，Baoding 071002，China）

A recognition method based on Euclidean algorithm is proposed to solve the problem of the blind recognition of BCH code．First，according to the cycle shifting code，a greatest common factor is achieved and many common factors constitute a coefficient matrix．Moreover，the times distribution of the greatest common factors were analyzed and the code length was obtained and polynomial generated by coefficient matrix．The recognition method is simple，and the fussy calculation of matrices is avoided．Both theoretical analysis and simulation results show that using fewer data can recognize effectively in no error and the recognition has better performance in BER．

BCH code；Euclidean algorithm；the greatest common factor；blind recognition

TN911．22

A

1000－1565（2012）04－0416－05

2012－01－10

河北省自然科學基金資助項目（F2009000224）

王蘭勛（1956－），男，河北安平人，河北大學副教授，主要從事數(shù)字通信與信息編碼方面研究．E－mail：wanglanxun＠yahoo．com．cn