帶擾動(dòng)參數(shù)的擬線性橢圓方程正解的存在性

孔麗華， 沈自飛

(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華 321004)

1001-5051(2012)04-0388-07

帶擾動(dòng)參數(shù)的擬線性橢圓方程正解的存在性

孔麗華， 沈自飛

(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華 321004)

研究了帶擾動(dòng)參數(shù)的擬線性橢圓方程

-ε2Δu-ε2Δ(u2)u+ε2V(x)u=h(u),x∈RN,N≥3

正解的存在性.其中V(x)為正的連續(xù)位勢(shì)函數(shù).在h(u)及V(x)滿足適當(dāng)?shù)臈l件下,建立了方程正解的存在性定理.

橢圓方程;變分法;臨界點(diǎn);正解

-ε2Δu-ε2Δ(u2)u+ε2V(x)u=h(u),x∈RN,N≥3

0 引 言

本文主要研究擬線性橢圓方程

正解的存在性.這類方程起源于對(duì)擬線性Schr?dinger方程

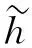
的研究,方程(2)的駐波解與方程(1)的解有密切的聯(lián)系.

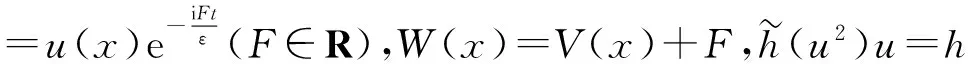
文獻(xiàn)[2-6]及其參考文獻(xiàn)討論了方程

非平凡弱解的存在性,這對(duì)于擬線性橢圓方程的進(jìn)一步研究有很大的幫助.例如,文獻(xiàn)[2]對(duì)于方程(3)中不同的非線性項(xiàng),通過(guò)極小化理論研究了方程正基態(tài)解的存在性;文獻(xiàn)[3]利用變量替換的方法,把擬線性橢圓問(wèn)題轉(zhuǎn)化為半線性問(wèn)題,通過(guò)山路引理,在Orlicz空間中證明了方程(3)正解的存在性;文獻(xiàn)[4]運(yùn)用了與文獻(xiàn)[3]相同的方法,在一般的Sobolev空間中對(duì)于不同類型的非線性項(xiàng),證明了方程(3)正解的存在性;文獻(xiàn)[5]研究了N=2的情形,假定非線性項(xiàng)h:R→R滿足臨界指數(shù)增長(zhǎng),通過(guò)Ambrosetti-Rabinowitz條件、山路引理及R2上的Trudinger-Moser型迭代不等式得到了問(wèn)題解的存在性.本文是在一般的Sobolev空間上考慮問(wèn)題,并且在非線性項(xiàng)前乘了一個(gè)小的擾動(dòng)常數(shù),通過(guò)山路引理及變量替換等理論討論了方程(1)解的存在性.

1 主要結(jié)果

本文運(yùn)用變分方法證明方程(1)在空間H1(RN)上正解的存在性,即相應(yīng)變分泛函

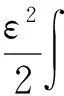
為了方便起見,本文用H替代H1(RN).

方程(1)中由于二階非齊次項(xiàng)Δ(u2)u的出現(xiàn),使得Jε(u)在空間H中不是良定的,因此不能直接討論Jε(u)臨界點(diǎn)的存在性.為了克服這類困難,將采用文獻(xiàn)[3-4]中變量替換的方法,首先引入函數(shù)f：

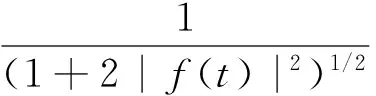
然后令u=f(v),λ=ε-2,將問(wèn)題轉(zhuǎn)化為研究下列相關(guān)泛函:

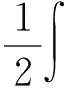
臨界點(diǎn)的存在性,即Iλ所對(duì)應(yīng)的Euler-Lagrange方程

解的存在性.下文的引理2將給出方程(1)的解與方程(5)的解之間的關(guān)系.

由于區(qū)域RN的無(wú)界性導(dǎo)致了緊性的缺失,所以為了尋找泛函Iλ的臨界點(diǎn),將證明Iλ滿足山路幾何性質(zhì),即

Γ={γ∈C([0,1],H):γ(0)=0,Iλ(γ(1))<0}≠?;

且

于是由Ekeland變分原理可知,在山路水平cλ處存在Iλ的一個(gè)Palais-Smale序列{vn}?H,即當(dāng)n→∞時(shí),

Iλ(vn)→cλ,I′λ(vn)→0.

由下文的引理3可知序列{vn}是有界的Palais-Smale序列.

如果位勢(shì)函數(shù)V(x)及非線性項(xiàng)h(s)滿足以下條件:

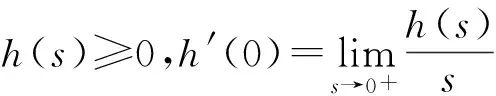
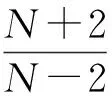
那么Iλ在空間H上是良定的,并且是C1的.

本文的主要結(jié)果是以下的定理1:

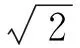
2 引 理

為了證明定理1,先給出幾個(gè)引理.

引理1[3-4]由方程(4)所定義的函數(shù)f(t)具有下列性質(zhì):

1)f是唯一的,f∈C2且是可逆的;

2)對(duì)所有的t∈R,f′(t)≤1,f2(t)/2≤tf′(t)f(t)≤f2(t);

3)對(duì)所有的t∈R, |f(t)|≤min{|t|, 21/4|t|1/2};

4)當(dāng)t→0時(shí),f(t)/t→1;

5)對(duì)所有的t>0,f(t)/2≤tf′(t)≤f(t);

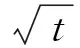
7)存在常數(shù)C>0,使得

如果u∈H∩L∞loc(RN),且對(duì)所有的φ∈C∞0(RN)有

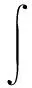
那么稱函數(shù)u:RN→R為方程(1)的弱解.

引理2方程(1)的解與方程(5)的解之間有以下關(guān)系:

1)若v∈H∩L∞loc(RN)是泛函Iλ的臨界點(diǎn),則f(v)為方程(1)的弱解;

2)若v是方程(5)的古典解,則f(v)為方程(1)的古典解.

證明 對(duì)于1),由引理1的2)和3)可知,|u|2=|f(v)|2≤|v|2且|▽u|2=|f′(v)|2|▽v|2≤|▽v|2,從而f(v)=u∈H∩L∞loc(RN).由于v是Iλ的一個(gè)臨界點(diǎn),于是對(duì)所有的ω∈H有

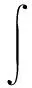
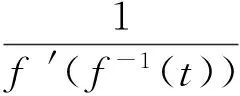
于是

從而對(duì)所有的φ∈C∞0(RN) 有f′(v)-1φ=(1+2|u|2)1/2φ,且

在式(7)中令ω=f′(v)-1φ,則由式(7)～式(10)易得式(6),即f(v)是方程(1)的弱解.

對(duì)于2),由于

故由式(8)可知

Δv=(1+2|u|2)1/2Δu+2u(1+2|u|2)-1/2|▽u|2,

所以

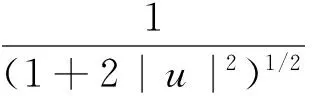
即

Δu+2|u|2Δu+2u|▽u|2=-(λh(u)-V(x)u).

注意到

2|u|2Δu+2u|▽u|2=Δ(u2)u,

因此有-ε2Δu-ε2Δ(u2)u=h(u)-ε2V(x)u,即2)成立.引理2證畢.

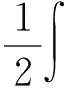
都有一個(gè)非平凡的臨界點(diǎn).

引理3[1]設(shè)X是一個(gè)Banach空間,其范數(shù)為‖5‖X,

Iλ(v)=A(v)-λB(v),?λ∈Ω

是空間X上的一族C1類泛函,其中Ω是一個(gè)區(qū)間, 如果

1)對(duì)?v∈X,B(v)≥0,且當(dāng)‖v‖X→∞時(shí),要么A(v)→∞,要么B(v)→∞.

2)存在v1,v2∈X,使得

其中,Γ={γ∈C([0,1],X):γ(0)=v1,γ(1)=v2}.那么對(duì)幾乎所有的λ∈Ω,存在序列{vn}?X使得:1){vn}是有界的;2)Iλ(vn)→cλ;3)I′λ(vn)→0.

引理4對(duì)于泛函

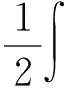
如果令

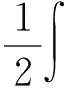
那么對(duì)所有的v∈H,有B(v)≥0,且當(dāng)‖v‖H→∞時(shí),有A(v)→∞.

證明 由(H1)可知,B(v)≥0.下證A(v)→∞.假設(shè)A(v)是有界的,即存在C>0,使得

則有

由(V2)可知,

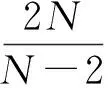
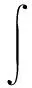
從而由式(11)和式(12)可得

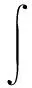
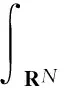
引理5如果(H1),(H2),(H3),(V1),(V2)成立,那么

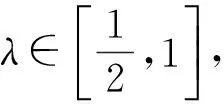
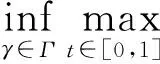
其中,Γ={γ∈C([0,1],H):γ(0)=0,γ(1)=v}.

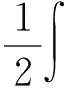
所以只需證明對(duì)任意的v∈H{0},存在t∈R,使得當(dāng)

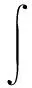
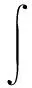
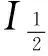
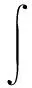
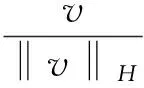
(13)

另一方面,由于v≠0,從而 |tnv(x)|→∞,于是當(dāng)n→∞時(shí),由條件(H3)及引理1的6)可知

∞.

這與式(13)矛盾.即1)成立.

對(duì)于2),由引理1的2)可知

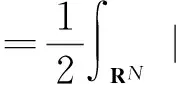
由文獻(xiàn)[1]的注3.3可知,

即證明了2).引理5證畢.

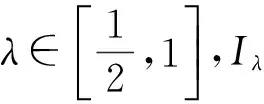
證明 因?yàn)閧vn}是有界的,所以{vn}必有收斂子列,不妨假設(shè)vn?vλ.下面證明vλ是Iλ的一個(gè)非平凡臨界點(diǎn).

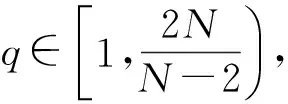
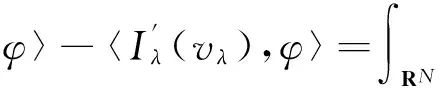
即證明了〈I′λ(vλ),φ〉=0.

其次,證明vλ≠0.若不然,則假設(shè)vλ= 0.一方面由文獻(xiàn)[1]的定理5.1可知

式(14)中:l≥1;vλ是Iλ的臨界點(diǎn)且

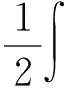
ωkλ為I∞λ的非平凡臨界點(diǎn)(k=1,2,…).而I∞λ對(duì)應(yīng)的Euler-Lagrange方程為

-Δv=g(v),

其中,g(v)=-V(∞)f(v)f′(v)+λh(f(v))f′(v).不難驗(yàn)證非線性項(xiàng)g滿足文獻(xiàn)[1]中定理3.2的條件(K0)至(K3),于是對(duì)于I∞λ的任一非平凡臨界點(diǎn)ωλ,有I∞λ(ωλ)>0, 從而由式(14),并注意到Iλ(vλ)=0,有

另一方面,假設(shè)ωλ為方程

-Δv+V(∞)f(v)f′(v)=λh(f(v))f′(v)

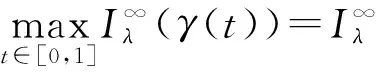
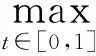
這與cλ≥mλ矛盾,即vλ≠0.引理6證畢.

3 定理1的證明

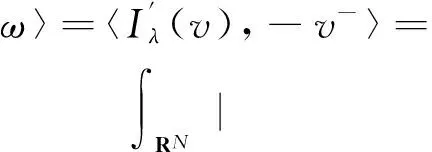
事實(shí)上,當(dāng)v≥0時(shí),有v-=0,從而有h(f(v))f′(v)(-v-)=0及f(v)(-v-)=0;當(dāng)v<0時(shí),有f(v)<0及-v-=v,于是有h(f(v))=0,即式(15)成立.

由式(15)有

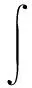
即

由f的定義得到

因此v-=0恒成立,即v≥0.定理1證畢.

[1]Jeanjean L,Tanaka K.A positive solution for a nonlinear Schr?dinger equation onRN[J].Indiana Univ Math,2005,54(2):443-464.

[2]Poppenberg M,Schmitt K,Wang Zhiqiang.On the existence of soliton solutions to quasilinear Schr?dinger equations[J].Calc Var Partial Differential Equations,2002,14(3):329-344.

[3]Liu Jiaquan,Wang Yaqi,Wang Zhiqiang.Soliton solutions for quasilinear Schr?dinger equations II[J].J Differential Equations,2003,187(2):473-493.

[4]Colin M,Jeanjean L.Solutions for a quasilinear Schr?dinger equation:a dual approach[J].Nonlinear Anal,2004,56(2):213-226.

[5]do ? Jo?o M B,Miyagaki Olímpio H,Soares Sérgio H M.Soliton solutions for quasilinear Schr?dinger equations:the critical exponential case[J].Nonlinear Anal,2007,67(12):3357-3372.

[6]Liu Jiaquan,Wang Zhiqiang.Soliton solutions for quasilinear Schr?dinger equations[J].Proc A M S,2003,131(2):441-448.

Theexistenceofpositivesolutionforthequasilinearellipticequationwithperturbationparameter

KONG Lihua, SHEN Zifei

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

It was showed the existence of positive solution for the quasilinear elliptic equation with perturbation parameter as

withV(x) a positive continuous potential function. Under some assumptions onV(x) and the nonlinear termh(u), the existence of positive solution for the above equation was obtained.

elliptic equation; variational method; critical point; positive solution

2012-04-21

國(guó)家自然科學(xué)基金資助項(xiàng)目(10971194)

孔麗華(1986-),女,江西吉安人,碩士研究生.研究方向：非線性泛函分析.

O177.91

A

(責(zé)任編輯 陶立方)