建筑力學教材中若干問題的探討
王淑琴
(甘肅工業職業技術學院,甘肅 天水 741025)
1 軸向拉壓斜截面部分
1)有關斜截面方位角的正負問題,一般教材是這樣論述的:規定從x軸開始逆時針轉到該截面外法線時,α為正,反之為負。這一規定中x軸的正向沒有指明。若取桿件左半部分為研究對象,x軸向右為正當然符合大多數人的習慣。但是如果取右半部分為研究對象,x軸的正向又如何,沒有規定。給計算斜截面的應力值帶來很多不便。個人認為應當統一此問題。可以規定:從所取對象(左半部分或右半部分)橫截面的外法線開始逆時針轉向該斜截面外法線,則α為正,反之為負。如圖1所示無論取左右哪部分為研究對象,對于同一斜截面α的正負都能統一。無論取桿件哪部分為研究對象都可以代入斜截面應力計算公式,得出統一的結果。

圖1 斜截面方位角α的正負示意圖
2)第二個問題是關于α的取值范圍也沒有明確交代,學生容易含糊不清。單從斜截面法線的旋轉角度來看應為0°<α<360°,但是由于我們只能取桿件的1/2來研究應力,所以α的取值范圍應為-90°<α<90°,無論取哪部分,在這個范圍內,α包括了所有的斜截面。如圖2a)所示,若取左半部分為研究對象n1,n4外法線所代表的斜截面,分別與n3,n2代表的斜截面實質為同一截面。取右半部分亦然。
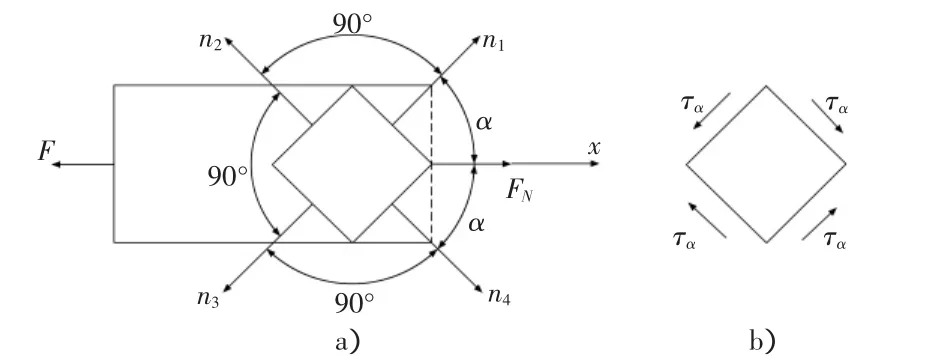
圖2 斜截面方位角α的取值
3)對于圍繞一點作出的六面體見圖2a),α的正向規定若同前,則α的取值范圍應為0°<α<360°。
順便再補充一點,講到這一節內容時也可用切應力公式給學生證明一下剪應力互生定理可有助于對此定理的理解,如圖2b)所示。
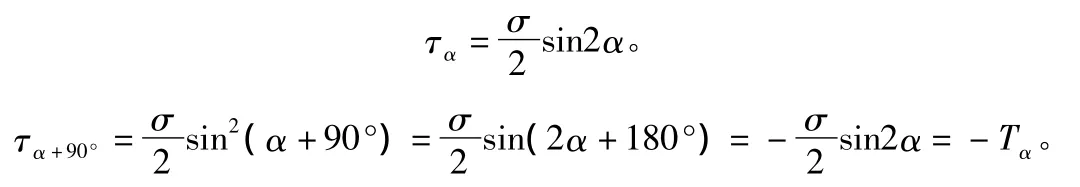
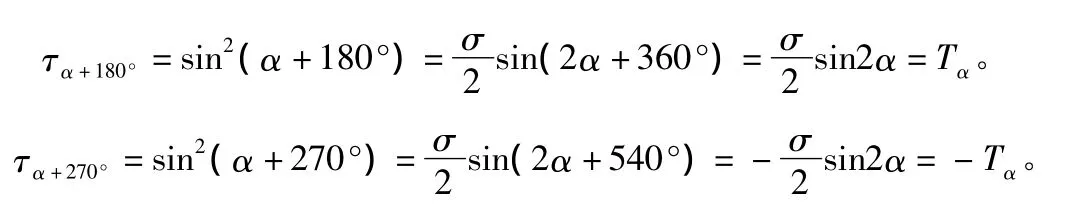
2 靜力學部分力偶及其基本性質一節有些問題也需商榷
教材在這一節敘述說:實踐中表明,力偶矩是衡量力偶轉動效果的物理量且為代數量,是在實踐中證明的。后在力偶性質一節又給予證明。證明的過程為:如果力矩能夠衡量力對物體的轉動效果這一命題成立,則力偶可看作兩個平行反向的力,求出兩力對任一點力矩之和可以得出力偶矩與矩心的位置無關的結論。所以力偶這一性質的證明是基于力矩的物理量的確定。后面平面力偶系的合成部分,有些教材對力偶的合成給了力學的證明,把幾組力偶改造成力臂相同的力偶后,形成共線力系,再來合成。這一證明過程從力學的角度看比較精巧,但是從邏輯上似乎沒法使人信服。既然力偶矩已經被確定為代數量,就不需進行上述有條件的力學合成,否則,與先前基本命題有矛盾。
所以可以說如果力矩能夠衡量力對物體的轉動效果這一命題成立,力偶矩作為一個可以衡量力偶轉動效果的物理量這一命題也應成立。力偶系的代數合成可能無需證明。
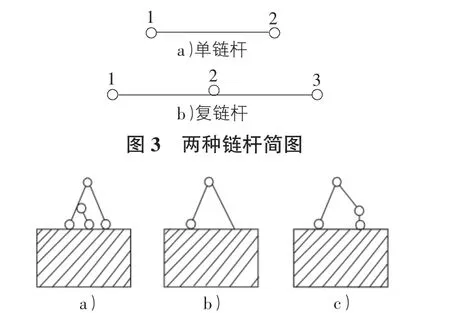
圖4 不是二元體的幾種情況
3 平面體系幾何性質
平面體系幾何性質一節,二元體是一個很重要的概念。能否正確判斷二元體決定著能否對體系作出正確的幾何分析。大多數教材給出的定義為“由兩根不共線的鏈桿連接一個節點的裝置或構造。”這個定義由于對鏈桿缺少準確界定,使多數學生對二元體的概念混淆不清,把貌似二元體的機構錯認為二元體造成判斷的錯誤。學習這一重要概念時,首先應讓學生明確這個鏈桿一定是單鏈桿,不是復鏈桿,見圖3。所以如果定義改為“由兩根不共線的單鏈桿連接一個節點的裝置或構造”可能更準確些。其次教會學生識別如圖4所示不是二元體的幾種情況也十分關鍵。
以上是本人在教學過程中的一點膚淺認識,提出來希望與同行切磋并能得到專家的指正。教材是教師傳遞知識的第一工具,只有吃透教材,不斷地完善教材才能更好的完成教學任務。但愿本文能起到拋磚引玉的作用,希望更多的有關人士關注一下教材的建設,為廣大師生服務。
[1] 于 英.建筑力學[M].北京:建筑工業出版社,2007.
[2] 西安交通大學材料力學教研室.材料力學[M].北京:人民教育出版社,1979.
[3] 龍馭球,包世華.結構力學教程[M].北京:高等教育出版社,2000.

