鋼—混疊合梁拱橋索梁錨固區合理應力狀態參數

李文龍 孫建淵

(同濟大學橋梁工程系，上海 200092)

1 概述

鋼—混疊合梁拱橋以其外形美觀、結構合理而在設計中越來越多地被采用，其吊桿與主梁之間的索梁錨固區則是該類橋梁設計中的重點。索梁錨固區利用吊桿將梁自重荷載和其所承擔的外荷載傳到拱肋上。在巨大的集中荷載作用下，索梁錨固區的構造形式和應力狀態復雜，橋梁設計時應將其作為關鍵環節予以分析。

拱橋吊桿與主梁的連接與錨固形式包括耳板、錨拉板、錨管和錨箱四種［1］。錨箱式連接通過錨固塊以焊接或栓接的形式與主梁相連，并將吊桿錨固于錨固塊上。為確保吊桿索力合理傳遞到主梁上，保證索梁錨固區應力狀態合乎規范規定，鋼錨箱的鋼板應采用合理的板厚規格。以蘭州某鋼—混疊合梁拱橋為例，選擇整體計算情況中處于最不利狀況的索梁錨固區段，用ANSYS建立合適的有限元分析模型，將各鋼板的板厚作為參數，通過對結構進行比較計算，分析不同鋼板的板厚對錨固區合理應力狀態的影響。

2 錨固區構造與有限元分析模型

2.1 索梁錨固區

索梁錨固區采用鋼錨箱的形式，是拱橋中關鍵的受力結構，同時把索力傳遞給主梁。鋼錨箱在吊桿方向利用焊縫將吊桿與鋼錨箱連接，將索力清晰地傳給主梁［2］。組成鋼錨箱的鋼板包括橫隔板、承壓板MJ1、錨固板MJ2和吊索導管(見圖1)。為了保證索梁錨固區的吊索索力合理傳遞到主梁上，鋼錨箱各組成板件應采用合理板厚規格。本文主要研究各板件厚度對索梁錨固區合理應力狀態的影響，并對下列六種情況進行計算比較，見表1。

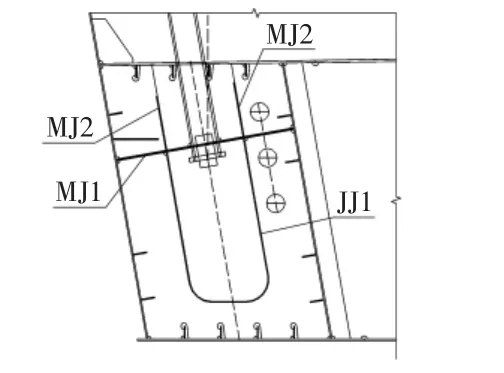
圖1 索梁錨固區鋼錨箱構造圖

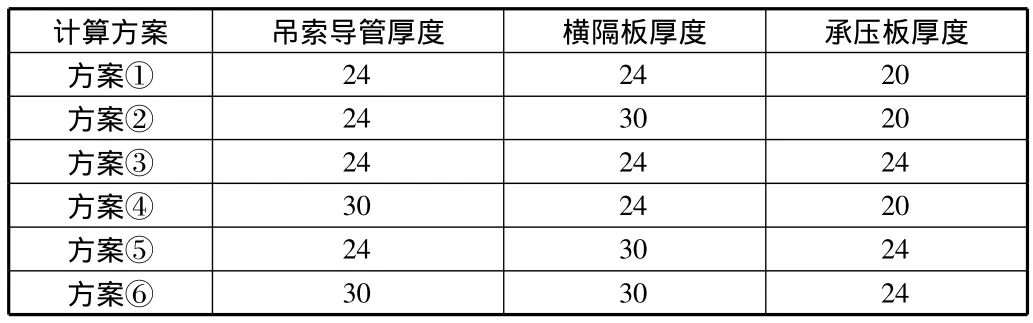
表1 用于分析的計算方案 mm

2.2 有限元分析模型

為探索索梁錨固區的應力分布狀態，采用基于數值方法的有限元軟件，截取整體計算情況中處于最不利狀況的索梁錨固區段，并基于圣維南原理明確合適的區段分析長度，同時確保在計算采用的邊界條件下，鋼錨箱應力狀態與實際情況接近。利用有限元分析鋼錨箱時，錨箱的計算長度有兩種方案可供選擇［3］:1)選擇處于鋼錨箱實際位置的區段，將遠離其的一端全固結處理;2)結合圣維南原理所論述的原則，分析區域應該考慮鋼錨箱臨近梁段的共同作用，并將計算區域兩側全固結。有限元分析應當最大限度地接近實際狀況，而方案②比較合理，因此，本文將利用方案②對索梁錨固區進行計算分析。本文參考的橋梁在設計時，橫隔板間距取為4 m，將有限元分析模型長度取為8 m，并將梁段兩側全固結(如圖2所示)。

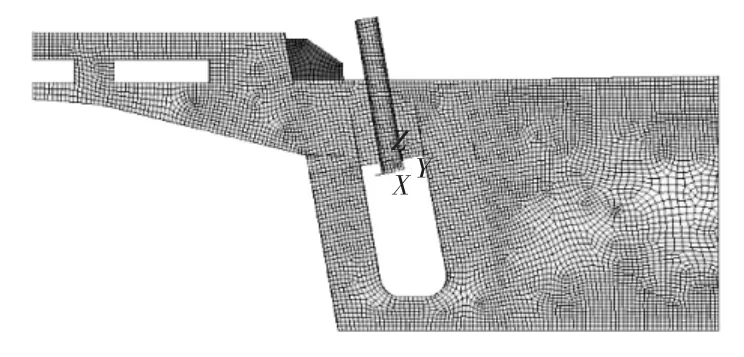
圖2 索梁錨固區有限元模型

利用大型通用有限元軟件ANSYS對鋼錨箱應力進行計算分析，并選用Shell63單元模擬鋼板。

3 結果分析

計算表明，索梁錨固區的應力分布狀態合理，各組成板件的應力云圖如圖3所示。

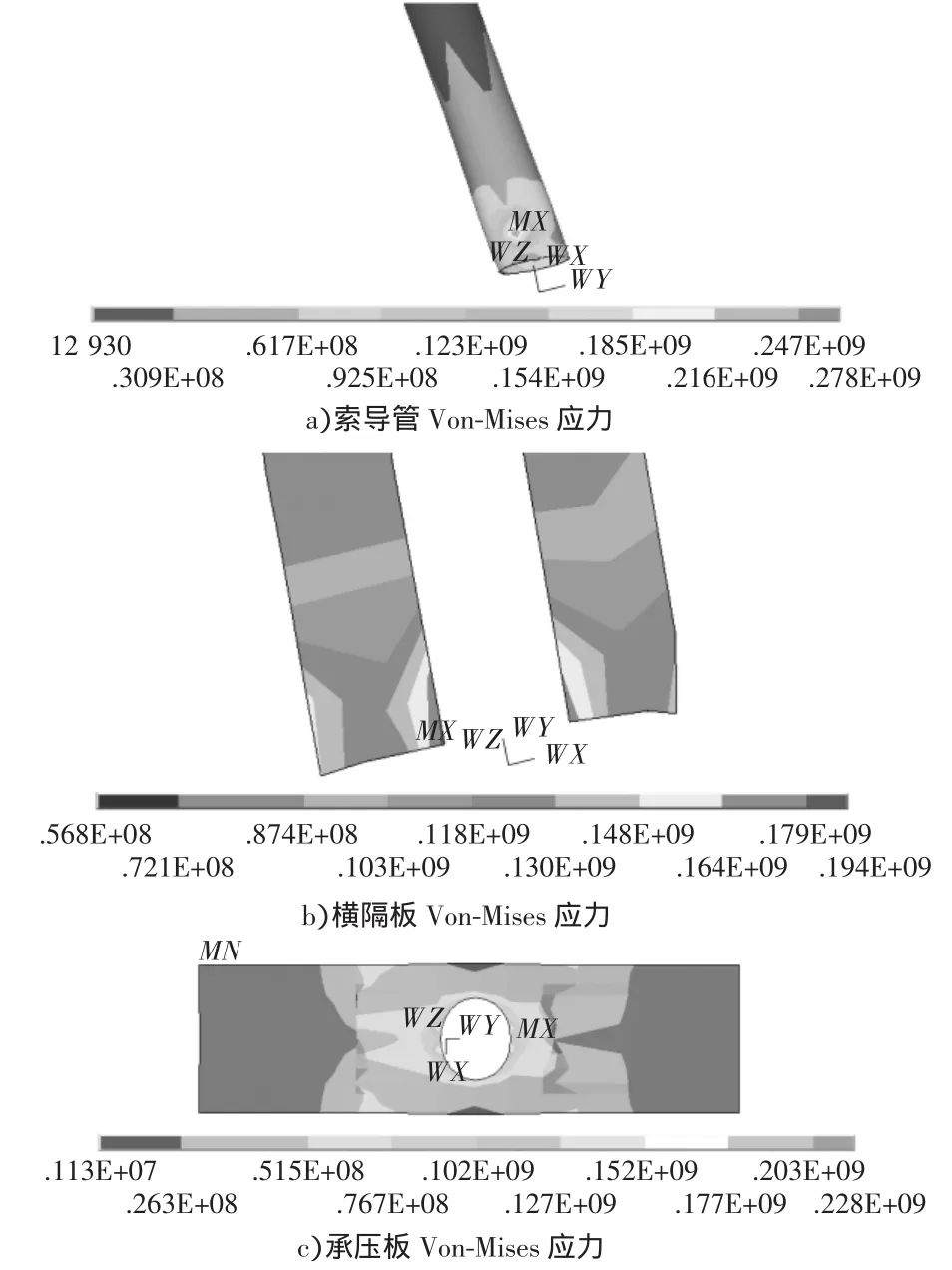
圖3 方案①錨固區各板件應力

各方案下索梁錨固區各構件的應力比較如圖4所示。

圖4 各方案下索梁錨固區應力比較

通過計算分析，將各方案結果進行比較，可以得到下述結論:

1)鋼錨箱整體性優越，吊桿與主梁之間的索力傳遞路徑清晰明白，傳力效果較好。

2)六種分析方案下，鋼錨箱的應力分布狀態整體較為接近。應力最大值位于索導管、橫隔板和承壓板的交界點區域，數值計算方法中該點位置存在局部應力集中現象。方案②與方案①比較、方案③與方案①比較、方案④與方案①比較可發現，增加橫隔板厚度、增加承壓板厚度、增加索導管厚度對降低應力最大值、改善應力狀態均有利，但增加索導管厚度的方案效果最好，其次是增加承壓板厚度與橫隔板厚度;方案⑤和方案⑥的計算結果表明，同時增加組成板件的厚度，其對索梁錨固區應力分布狀態的改善效果并沒有同時疊加。從而得出，增加索導管的厚度最利于索梁錨固區形成合理應力狀態，同時增加橫隔板厚度與承壓板厚度也能繼續改善應力分布，但并不具備明顯的疊加效果。所以，為保證錨固處的應力狀態合理，設計時應考慮首先增加索導管厚度，其次是承壓板，最后是橫隔板。

4 結語

索梁錨固區采用了鋼錨箱形式，雖然組成鋼板較多，但鋼錨箱整體性優越，吊桿與主梁之間的索力傳遞路徑清晰明白，傳力效果較好。組成鋼錨箱的鋼板規格對索梁錨固區的應力狀態均有影響，但影響大小不一。從有限元計算結果比較來看:索導管的板厚規格對錨固區應力狀態的影響最大，其次是承壓板和橫隔板板厚規格;鋼錨箱各板件板厚同時增加，對應力狀態的影響效果并不會同時疊加。為保證索梁錨固區的應力狀態合理，同時使得設計經濟可行，鋼錨箱各板件應有先后有限度的采用合適的板厚規格。

［1］李小珍，蔡 婧，強士中.大跨度鋼箱梁斜拉橋索梁錨固結構型式的比較研究［J］.土木工程學報，2001，37(3):73-79.

［2］常文潔，邱文亮，夏文來.斜跨鋼拱橋索梁錨固區主梁腹板加勁肋優選［J］.武漢理工大學學報，2010，32(1):140-142.

［3］萬 臻，李 喬，毛學明.大跨度斜拉橋鋼錨箱式索梁錨固結構空間有限元模型比較分析［J］.四川建筑科學研究，2006，32(1):26-30.