地空導(dǎo)彈三點(diǎn)法三維運(yùn)動(dòng)學(xué)彈道建模與仿真

張大元, 趙玉芹, 雷虎民, 吳一鳴

(空軍工程大學(xué) 導(dǎo)彈學(xué)院, 陜西 三原 713800)

地空導(dǎo)彈三點(diǎn)法三維運(yùn)動(dòng)學(xué)彈道建模與仿真

張大元, 趙玉芹, 雷虎民, 吳一鳴

(空軍工程大學(xué) 導(dǎo)彈學(xué)院, 陜西 三原 713800)

針對(duì)三點(diǎn)法三維運(yùn)動(dòng)學(xué)彈道仿真問題,建立了兩種仿真模型。第一種模型采用數(shù)值積分算法求解三點(diǎn)法運(yùn)動(dòng)學(xué)方程組,求解過程較為復(fù)雜;第二種模型利用三維空間相關(guān)幾何知識(shí),將求解三點(diǎn)法三維運(yùn)動(dòng)學(xué)彈道的圖解法轉(zhuǎn)化為求解一元二次方程的問題,使求解過程簡(jiǎn)單直觀。最后,對(duì)兩種模型進(jìn)行了仿真,并將其應(yīng)用到地空導(dǎo)彈制導(dǎo)控制系統(tǒng)的仿真研究中,將理想彈道與控制彈道進(jìn)行了對(duì)比。結(jié)果表明,兩個(gè)模型均解決了一般情形下三點(diǎn)法三維運(yùn)動(dòng)學(xué)彈道求解的問題,為三點(diǎn)法三維制導(dǎo)律以及彈道特性研究提供了一種方法。

地空導(dǎo)彈; 三點(diǎn)法; 三維運(yùn)動(dòng)學(xué)彈道; 仿真

引言

三點(diǎn)法因?qū)崿F(xiàn)較為簡(jiǎn)單,一直是采用遙控制導(dǎo)體制的地空導(dǎo)彈常用的導(dǎo)引方法,繪制其三維運(yùn)動(dòng)學(xué)彈道不僅是研究該導(dǎo)引規(guī)律以及彈道特性的需要,而且在地空導(dǎo)彈全彈道仿真中,需要繪制理想運(yùn)動(dòng)學(xué)彈道來為仿真彈道提供參考,是進(jìn)行制導(dǎo)控制系統(tǒng)仿真的一個(gè)環(huán)節(jié)。

針對(duì)三點(diǎn)法的運(yùn)動(dòng)學(xué)彈道,許多有關(guān)導(dǎo)彈飛行力學(xué)的文獻(xiàn)中都有描述,也有許多學(xué)者研究了三點(diǎn)法彈道的繪制方法,如文獻(xiàn)[1]給出了在鉛垂平面內(nèi)三點(diǎn)法運(yùn)動(dòng)學(xué)方程組,并詳細(xì)描述了三點(diǎn)法運(yùn)動(dòng)學(xué)彈道的圖解法;文獻(xiàn)[2]對(duì)三點(diǎn)法原理進(jìn)行了詳細(xì)的分析,并給出了鉛垂平面內(nèi)采用三點(diǎn)法抗擊勻速直線運(yùn)動(dòng)目標(biāo)情形下,運(yùn)動(dòng)學(xué)彈道的解析方法;文獻(xiàn)[3]也給出了垂直平面內(nèi)目標(biāo)勻速直線運(yùn)動(dòng)情形下的三點(diǎn)法運(yùn)動(dòng)學(xué)彈道的解析解。但是,即使在鉛垂平面內(nèi),當(dāng)目標(biāo)機(jī)動(dòng)時(shí),運(yùn)動(dòng)學(xué)彈道的求解就比較困難了,更不用說三維空間中目標(biāo)機(jī)動(dòng)的情形。所以,研究三點(diǎn)法三維空間攔截機(jī)動(dòng)目標(biāo)的運(yùn)動(dòng)學(xué)彈道是很有意義的。

本文從求解導(dǎo)彈三維運(yùn)動(dòng)學(xué)方程組入手,建立了兩種模型,第一種是適用于三維運(yùn)動(dòng)空間和目標(biāo)機(jī)動(dòng)情形的三點(diǎn)法運(yùn)動(dòng)學(xué)彈道仿真模型;第二種是參考三點(diǎn)法圖解原理,結(jié)合三維空間相關(guān)幾何知識(shí),使彈道求解過程簡(jiǎn)單、直觀。

1 參考坐標(biāo)系

1.1 測(cè)量坐標(biāo)系

研究地空導(dǎo)彈三點(diǎn)法導(dǎo)引規(guī)律,通常采用測(cè)量坐標(biāo)系Oxjyjzj,該坐標(biāo)系原點(diǎn)選在地面制導(dǎo)站上,Oxj軸在制導(dǎo)站和目標(biāo)的連線上,指向目標(biāo)為正;Oyj軸在通過Oxj軸的鉛垂平面內(nèi),垂直于Oxj軸向上為正;Ozj軸按右手定則確定。測(cè)量坐標(biāo)系可由地面坐標(biāo)系經(jīng)由兩次旋轉(zhuǎn)得到,如圖1所示。圖中,ε為高低角,β為方位角。

圖1 測(cè)量坐標(biāo)系和地面坐標(biāo)系

測(cè)量坐標(biāo)系相對(duì)地面坐標(biāo)系的轉(zhuǎn)換矩陣為:

(1)

1.2 彈道坐標(biāo)系

彈道坐標(biāo)系Oxcyczc,該坐標(biāo)系原點(diǎn)選在飛行器質(zhì)心上,Oxc軸與飛行器速度矢量重合,向前為正;Oyc軸在通過Oxc軸的鉛垂平面內(nèi),垂直于Oxc軸向上為正;Ozc軸按右手定則確定。彈道坐標(biāo)系可由地面坐標(biāo)系經(jīng)由兩次旋轉(zhuǎn)得到,如圖2所示。圖中,θ為彈道傾角,φc為彈道偏角。

圖2 彈道坐標(biāo)系和地面坐標(biāo)系

彈道坐標(biāo)系相對(duì)地面坐標(biāo)系的轉(zhuǎn)換矩陣為:

(2)

2 三點(diǎn)法導(dǎo)引規(guī)律運(yùn)動(dòng)學(xué)方程組的建立

所謂三點(diǎn)法導(dǎo)引規(guī)律是指:導(dǎo)彈在攻擊目標(biāo)的飛行過程中,使導(dǎo)彈、目標(biāo)和制導(dǎo)站始終在一條直線上。其導(dǎo)引原理如圖3所示。圖中,R,Rm代表導(dǎo)彈和目標(biāo)的斜距。

圖3 三點(diǎn)法理想導(dǎo)引示意圖

根據(jù)運(yùn)動(dòng)學(xué)規(guī)律,在測(cè)量坐標(biāo)系中,制導(dǎo)站與導(dǎo)彈之間的運(yùn)動(dòng)學(xué)關(guān)系為:

(3)

式中,Vxj,Vyj,Vzj分別為導(dǎo)彈運(yùn)動(dòng)速度在測(cè)量坐標(biāo)系沿各坐標(biāo)軸的分量。

下面分別求解式(3)所需的3個(gè)速度分量。首先,將導(dǎo)彈速度從彈道坐標(biāo)系分解到地面坐標(biāo)系,依據(jù)式(2),得:

(4)

式中,V為導(dǎo)彈速度;Vxd,Vyd,Vzd為導(dǎo)彈速度在地面坐標(biāo)系各坐標(biāo)軸的分量。

再利用式(1),得:

(5)

化簡(jiǎn)式(4)、式(5)得:

(6)

這樣,由式(3)和式(6)可得導(dǎo)彈相對(duì)制導(dǎo)站的運(yùn)動(dòng)學(xué)方程為:

(7)

同理可求得:

(8)

式中,Vmxj,Vmyj,Vmzj分別為目標(biāo)運(yùn)動(dòng)速度在測(cè)量坐標(biāo)系沿各坐標(biāo)軸的分量;Vm為導(dǎo)彈速度;θm,φcm分別為目標(biāo)的彈道傾角和彈道偏角;βm,εm分別為目標(biāo)的偏航角和高低角。

同式(7),可求得目標(biāo)相對(duì)于制導(dǎo)站的運(yùn)動(dòng)規(guī)律為:

(9)

這樣,式(7)和式(9)就構(gòu)成了求解三點(diǎn)法運(yùn)動(dòng)學(xué)彈道所需的6個(gè)方程。為求解該方程,要求的已知量包括目標(biāo)運(yùn)動(dòng)參數(shù)(Vm,θm,φcm,εm,βm)和導(dǎo)彈速度V,另外,還需要三點(diǎn)法的導(dǎo)引方程:

(10)

這樣,方程組(7)、(9)、(10)共8個(gè)方程,8個(gè)未知數(shù),方程組可以求解。

3 仿真模型

3.1 仿真模型1

仿真模型1采用四階龍格庫塔法求解由式(7)、式(9)和式(10)構(gòu)成的運(yùn)動(dòng)方程組,由于導(dǎo)彈的彈道偏角和傾角不是顯式表達(dá)的,故需要轉(zhuǎn)化求解。

若是導(dǎo)彈始終按照三點(diǎn)法的導(dǎo)引方程飛行,則有:

(11)

這樣,就可以將式(7)和式(9)中的第二、第三個(gè)方程聯(lián)立:

(12)

(13)

考慮到

中沒有直接使用彈道傾角和彈道偏角的值,所以沒有必要求解θ和φc的具體值,只要將其正弦或余弦值作為一個(gè)整體求解即可。

將式(13)代入式(12)得:

(14)

為使方程簡(jiǎn)潔,作以下?lián)Q元:

(15)

由式(14)和式(15)可得:

(16)

(17)

化簡(jiǎn)式(17),得:

x2-2mpx-(n2-n2q2-p2)=0

(18)

求解該式,x即為所得正根,將x代入式(16)第一個(gè)方程,可得y值,將x,y代入

(19)

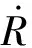
采用仿真模型1進(jìn)行仿真驗(yàn)證的流程如下:

(1)給出目標(biāo)運(yùn)動(dòng)規(guī)律(包括初始位置Rm0,εm0,βm0，彈道傾角及偏角變化規(guī)律，目標(biāo)速度Vm);導(dǎo)彈初始位置R0,ε0,β0;導(dǎo)彈速度V;

(2)積分式(9),求解目標(biāo)位置參數(shù)Rm,εm,βm;

(3)求解式(18),利用其結(jié)果積分式(19),得到導(dǎo)彈斜距R;

(4)根據(jù)導(dǎo)引規(guī)律,導(dǎo)彈高低角和方位角與目標(biāo)一致,即ε=εm,β=βm;

3.2 仿真模型2

三點(diǎn)法導(dǎo)引彈道用圖解法更為直觀方便,但是圖解結(jié)果不便于轉(zhuǎn)化為坐標(biāo)值,仿真模型2把圖解法轉(zhuǎn)化為一元二次方程。

參照?qǐng)D3,設(shè)導(dǎo)彈初始位置為D(xd1,yd1,zd1),目標(biāo)初始位置為M(xm1,ym1,zm1),經(jīng)過時(shí)間Δt,目標(biāo)飛行至M′(xm2,ym2,zm2),導(dǎo)彈在服從導(dǎo)引律的情況下,應(yīng)該飛行至D′(xd2,yd2,zd2),假設(shè)在時(shí)間間隔較小的情況下,導(dǎo)彈速度保持勻速,該導(dǎo)彈新坐標(biāo)即為所求值。

由導(dǎo)引規(guī)律知,導(dǎo)彈新坐標(biāo)滿足以下條件:

由條件(1)和(2)可以列寫等價(jià)方程:

(20)

令

(21)

將式(21)代入式(20),得:

(22)

求解該方程,得k值。

依據(jù)式(20)求得導(dǎo)彈坐標(biāo):

(23)

若是有兩個(gè)k值,則分別求解導(dǎo)彈坐標(biāo),然后選擇導(dǎo)彈yd2滿足yd2≥yd1的k值,這是因?yàn)榈乜諏?dǎo)彈一般是向上飛的。

采用仿真模型2進(jìn)行仿真的步驟如下:

(1)給出導(dǎo)彈和目標(biāo)初始位置D(xd1,yd1,zd1),M(xm1,ym1,zm1);導(dǎo)彈和目標(biāo)速度V,Vm;仿真步長(zhǎng)Δt;

(2)求解目標(biāo)坐標(biāo)M′(xm2,ym2,zm2);

(3)依據(jù)式(20)～ 式(23)求解導(dǎo)彈的坐標(biāo)D′(xd2,yd2,zd2);

4 仿真算例

假設(shè)某地空導(dǎo)彈按照三點(diǎn)法攔截作等高圓弧形機(jī)動(dòng)的目標(biāo)。目標(biāo)初始機(jī)動(dòng)過載為5,速度為700 m/s,位置M(18 373,15 000,-18 373) m,開始機(jī)動(dòng)時(shí)間為0 s。導(dǎo)彈初始速度為800 m/s,位置D(0,0,0) m。

采用Matlab語言對(duì)兩個(gè)模型進(jìn)行了仿真,分別繪制了兩種模型在攔截同一機(jī)動(dòng)目標(biāo)時(shí)的理想彈道曲線,如圖4所示。

圖4 三點(diǎn)法三維運(yùn)動(dòng)學(xué)彈道

最后,將所設(shè)計(jì)的理想運(yùn)動(dòng)學(xué)彈道求解模型應(yīng)用于全彈道仿真軟件中,作為理想彈道與控制彈道進(jìn)行比較。在仿真中,導(dǎo)彈速度是由導(dǎo)彈動(dòng)力學(xué)方程求解得到的控制速度,從而說明當(dāng)導(dǎo)彈速度為變量時(shí),兩個(gè)仿真模型依然適用。仿真結(jié)果如圖5所示。由圖5可知,實(shí)際彈道總是圍繞理想運(yùn)動(dòng)學(xué)彈道運(yùn)動(dòng)的[4-5],所以理想運(yùn)動(dòng)學(xué)彈道可以用來檢驗(yàn)控制彈道的準(zhǔn)確程度,從而檢驗(yàn)導(dǎo)彈制導(dǎo)控制系統(tǒng)的精度。

圖5 控制彈道與理想彈道的比較

5 結(jié)束語

通過以上仿真分析以及模型最后的使用效果可知,文中建立的地空導(dǎo)彈三點(diǎn)法三維運(yùn)動(dòng)學(xué)彈道的兩種仿真模型都是有效的,模型精度都比較高,但在實(shí)際的仿真中,常采用數(shù)值積分的方法,可是在理解三點(diǎn)法的原理時(shí),圖解法更容易讓人接受,所以兩種模型各有優(yōu)劣。

當(dāng)今,仍有很大一部分新型地空導(dǎo)彈武器采用了三點(diǎn)法這種實(shí)現(xiàn)簡(jiǎn)單、精度較高的導(dǎo)引方法,本文為三點(diǎn)法三維導(dǎo)引規(guī)律以及三點(diǎn)法的應(yīng)用研究提供了一種有力的工具。

[1] 雷虎民.導(dǎo)彈制導(dǎo)與控制原理[M].北京:國(guó)防工業(yè)出版社,2009:82-89.

[2] 周慧鐘,李忠應(yīng),王瑾.有翼導(dǎo)彈飛行動(dòng)力學(xué)[M].北京:北京航空航天大學(xué)出版社,1987.

[3] 朱衛(wèi)兵,張耀良.戰(zhàn)術(shù)導(dǎo)彈三點(diǎn)法遙控制導(dǎo)彈道方程的解析解[J].彈箭與制導(dǎo)學(xué)報(bào),2006,26(1):245-247.

[4] 鄧方林,黃先祥.彈道導(dǎo)彈六自由度仿真決策系統(tǒng)設(shè)計(jì)與研制[J].系統(tǒng)仿真學(xué)報(bào),2004,16(2):186-189.

[5] Curtis P Mracek,Ridgely D Brett.Optimal control solution for dual(tail and canard)controlled missiles[R].AIAA-2006-6569,2006.

Modelingandsimulatingonkinematictrajectoryofground-to-airmissilecontroledbythree-pointmethod

ZHANG Da-yuan, ZHAO Yu-qin, LEI Hu-min, WU Yi-ming

(Missile Institute, Air Force Engineering University, Sanyuan 713800, China)

Two new simulation models are established for the simulation of three-dimensional kinematic trajectory of ground-to-air missile controled by a three-point method. The first model is to solve the equation of the three-point method by integral method, which is complex; The second model translates the geometrical method into a unitary-quadratic equation, which is simple and intuitional. At last, the two models are simulated and applied in the research of the guidance and control sysytem for ground-to-air missile, the ideal trajectory is contrasted with the real one. The results show that both of the models can solve the problem of drawing three-dimensional kinematic trajectory of the three-point method, as a result, three-dimensional guidance-law of the three-point method and characters of the trajectory can be researched easily.

ground-to-air missile; three-point method; three-dimensional kinematic trajectory; simulation

2011-04-06;

2011-08-23

航空科學(xué)基金資助(20090196005；20100196002)

張大元(1987-),男,山東滕州人,碩士,主要從事導(dǎo)彈控制系統(tǒng)研究；

趙玉芹(1961-),男,山東汶上人,副教授,碩士生導(dǎo)師,主要從事防空導(dǎo)彈引信技術(shù)研究。

TJ762.13; TJ765

A

1002-0853(2012)01-0057-04

(編輯：姚妙慧)