低成本的永磁同步電動機控制系統仿真

倪 攀，王東萃，傅振興

(上海汽車集團股份有限公司技術中心，上海 201804)

0 引 言

永磁同步電動機矢量控制系統離不開對轉子位置的檢測。當前常用的永磁同步電動機轉子位置傳感器有光電編碼器、旋轉變壓器、線性霍爾和開關型霍爾等。除了開關型霍爾，其它幾種位置傳感器都價格偏高，不適用于對成本較為敏感的行業(如家電行業)。而無位置傳感器技術當前在理論和技術上不夠完善，實現起來難度較大，且在起動和低速時的轉子位置估算誤差較大。開關型霍爾的特點是價格低，只能提供離散的轉子位置信號，無法單獨實現永磁同步電動機的矢量控制。因此，綜合考慮成本、可靠性以及開發難度等因素，選用開關型霍爾作為位置傳感器，再配之以合適的轉子位置估算方法實現，永磁同步電動機矢量控制的方案具有廣泛的應用價值。

本文采用id=0的矢量控制策略，并用速度、電流雙閉環搭建永磁同步電動機控制系統仿真模型。轉子位置檢測裝置采用兩相開關型霍爾。電機轉動時得到四個離散的開關信號。轉子角度估算模塊通過這四個離散的霍爾信號再使用合適的角度估算方法估算轉子的實際角度和實際轉速。本文使用常用的幾種角度估算方法搭建仿真模塊并加以運行比較，對于不同的需求可選用不同的角度估算方法。

1 永磁同步電動機id=0矢量控制策略

對電機的的各種控制歸根結底是對電機轉矩的控制。永磁同步電動機的轉矩矢量方程如下:

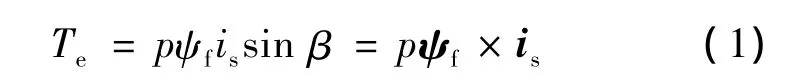
式(1)說明，在旋轉dq軸系內通過控制is的幅值和相位，就可控制永磁同步電動機的轉矩。由于轉子永磁體產生的磁鏈恒定不變，可采用磁場定向得旋轉坐標系的d軸方向與ψf方向一致，q軸為逆時針方向超前d軸電角度。通過Clarke變換和Park變換可得到如圖1所示的矢量圖。因此由式(1)可得:

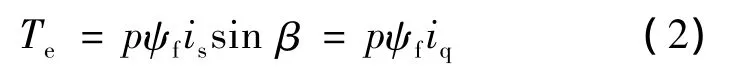
圖1 永磁同步電動機矢量圖

式(2)表明:在這種情況下，只要控制iq就可以控制電磁轉矩的大小。這就是id=0的控制思想，即控制β=90°電角度。is=jiq，定子電流全部轉化為轉矩電流。圖1中雖然轉子以電角度ω旋轉，但是在dq軸系中ψf與is始終保持相對靜止。從轉矩生成的角度來看，面裝式永磁同步電動機可等效為他勵直流電動機。

2 基于開關型霍爾的角度估算方法

當轉子轉動時，霍爾元件輸出的位置信號為兩相相差 90°、脈寬 180°電角度的方波，這些信號把360°的電角度劃分為4個90°的位置區間，如圖 2所示。因此，根據霍爾信號可判斷永磁體轉子在哪個區間。

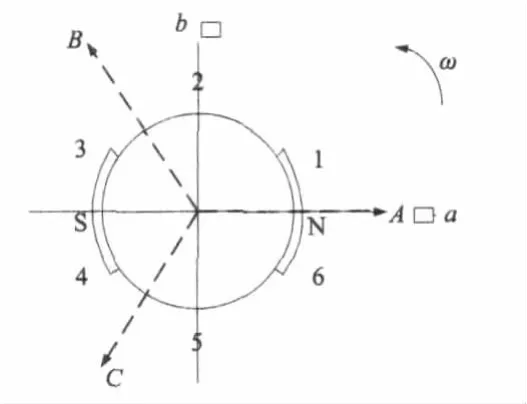
圖2 開關霍爾元件與轉子磁場的相對關系

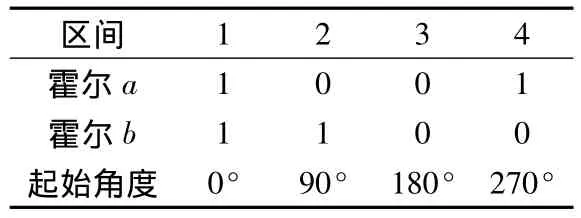
表1 霍爾與區間對應關系

對于永磁同步電動機轉子位置檢測方法的應用成本，基于兩相正交鎖存型霍爾相對基于三相對稱鎖存型霍爾較低，并且降低了安裝誤差的影響，電機在高速運轉時較基于三相對稱霍爾所需的角度估算次數少，并且因為轉速快，動態誤差也相差無幾。基于單個鎖存霍爾的永磁同步電動機轉子位置檢測方法相對前兩種方法，應用成本最低，并且避免了前兩種方法在安裝過程中所產生的霍爾位置不對稱誤差。但是單個霍爾不能提供電機的轉向信息，只能提供速度和位置信號，這對于如洗衣機等需要頻繁正反轉的場合并不適用。另外在電機加減速運行時，該方法相對于前兩種方法得到的位置檢測誤差更大。轉子位置的估計方法可通過硬件數字電路實現，也可由軟件算法完成。本文介紹4種軟件算法實現，省略了外圍硬件電路。

(1)勻速時轉子位置估算——方法一

此方法是用轉子轉過前一個扇區的平均速度假定為當前扇區的速度。當前扇區的平均速度ωid由轉子經過前一個扇區所需時間算出。當前的轉子位置θid等于該扇區的起始角度θi加上從θi旋轉經過的角度。計算公式如下:

式中:T為采樣周期;k為ti到tid間的采樣周期次數。

(2)非勻速時轉子位置估算——方法二

當電機勻速運行時，采用上一個位置估算法得到的轉子位置信號與實際轉子位置信號一致。但當電機轉速變化時，由上述算法得到的轉子位置信號就存在較大的誤差了。對于此問題，文獻［3］將一階算法中引入電機平均加速度的概念。其分析如圖3所示。

圖3 霍爾信號區間

其算法是:

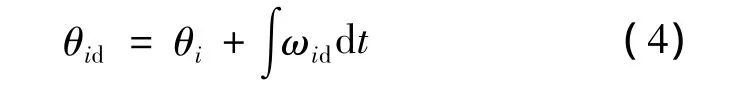
式中:ωid的當前扇區速度:

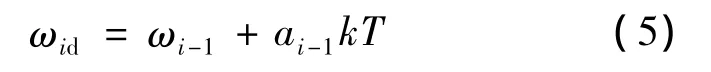
加速度ai－1由前一個扇區和前兩個扇區的平均速度計算出來:

因此，式(4)可轉化為:

(3)改進型非勻速時轉子位置估算——方法三

為了獲得更高精度的角度位置，文獻［6］提出也可對式(5)進行改進。由于式(5)中的ωi－1是上個扇區的平均速度，因此它不是ti時間點的速度。理論上在電機加速時，以它為初速度算出來的ωid會低于實際速度。因此，通過對方法二中的速度估算公式的改進可以達到增加角度估算精度的目的，而該方法中的其他計算公式仍沿用方法二中的公式。對式(5)進行如下改進:

(4)低速時轉子位置估算——方法四

為了解決電機低速運行問題，文獻［4］提出不顧電機的實際速度，直接使用用戶要求的速度來計算轉子的即時位置。即ωid不通過計算得到，直接為系統的給定速度。這樣大大降低了運算器的運算負荷，在低速時也可獲得不錯的運行性能。

3 轉子位置校正

在電機的實際運行過程中，利用上述方法進行轉子位置預估，角速度的波動是不可避免的。例如起動、突然加速、加載降速等情況產生的角速度的變化會使轉子空間角度的估算產生很大的誤差，造成電機運行不穩定。估算的角度誤差主要由穩態估算誤差和動態估算誤差兩部分組成。穩態估算誤差是指由于采樣周期的量化誤差和由于計數器位數造成的有限字長效應。動態估算誤差主要由ωr的預估誤差引起。為了保證在此情況下的轉子轉角計算結果不超出或太滯后所在位置區間的臨界值，位置信號及時校正是必須的。因此在以上各種估算方法中都需要加入轉子位置校正，以提高系統的穩定性。轉子位置校正就是在每次霍爾信號來臨后，將轉子位置重新校正。基本方法是在霍爾信號每次變化時，不管之前的計算角度結果如何，都按表1的起始角度開始估算。反轉時，只要將起始角度都加上90°電角度即可。這樣，每90°電角度就會發生一次轉子角度校正，保證了系統的抗干擾性。

4 角度輸出仿真模塊

(1)霍爾信號產生模塊

為了搭建基于兩相對稱霍爾的系統，我們必須自己搭建雙霍爾信號產生模塊的。可以參考如圖4所示的方法搭建。

圖4 霍爾產生模塊

(2)角度校正模塊

每當霍爾信號改變時，不管哪種角度估算方法都需要角度校正或者說需要一個區間的初始角度，這樣可以增加系統的穩定性。校正仿真如圖5所示。

圖5 角度校正模塊

該模塊要放在Triggered Subsystem模塊，觸發源是兩相霍爾信號。Trigger type設為either，即有上升沿或下降沿霍爾觸發脈沖時都能觸發此模塊。兩個霍爾元件按二進制的形式計算，得到的值再根據電機的旋轉方向判斷在哪個扇區，給出不同的角度初始值。如正轉則按照表1給定角度初始值，反轉則需在表1的基礎上每個初始角度加上90°電角度。

(3)速度估算模塊和角度計算模塊

以速度估算方法二為例，搭建模塊如圖6所示。

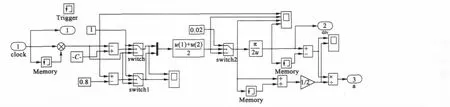
圖6 方法二中的速度估算

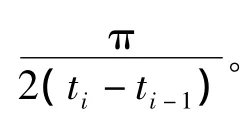
圖7 方法二中的角度計算

5 系統仿真模型搭建和驗證

在本設計中，我們直接選用MATLAB R2010A中的SimPowerSystems仿真工具箱中已有的逆變器模塊。永磁同步電動機參數設置為:極數p=4，額定轉矩0.8 N·m，電壓310 V(DC)，額定轉速3000 r/min。系統總框架圖如圖8所示。

圖8包括:霍爾信號生成模塊，四種角度估算方法模塊、轉速電流PI調節模塊、abc_to_dq轉換模塊、inverse Park模塊、SVPWM模塊、逆變器、永磁同步電機和多個示波器模塊。PWM載波周期為0.0001 s。給定速度為3000 r/min，電機負載起動，負載轉矩為0.8 N·m。本文給出的永磁同步電動機控制系統仿真結果是基于角度估算方法二，其它角度估算方法給出角度估算輸出曲線。

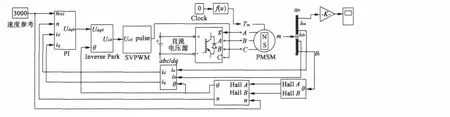
圖8 系統仿真框圖

整個永磁同步電動機控制系統的電流，轉速和轉矩如圖9所示。

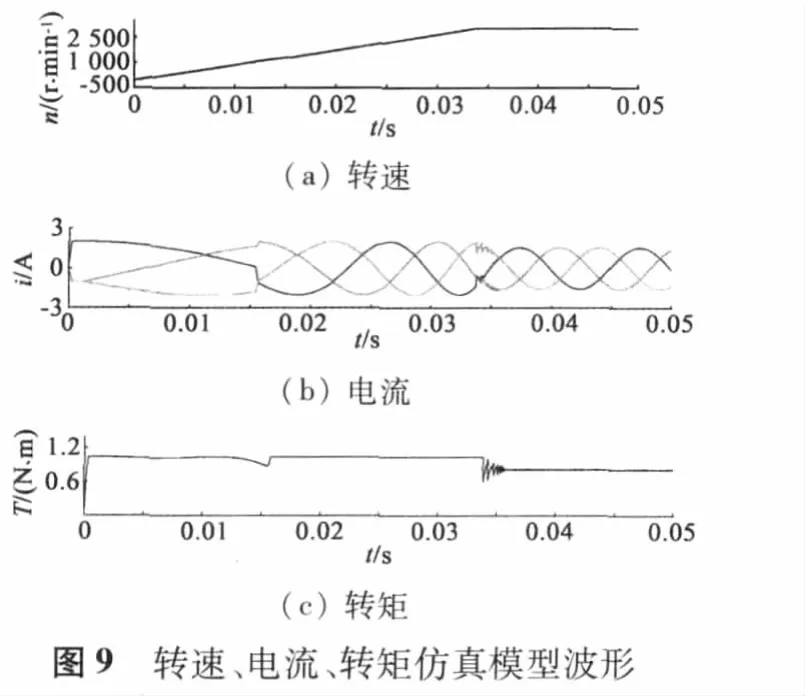
從圖9中可以看出轉速能較平滑起動。定子三相電流在起動之初有波動，也導致了電機轉矩在起動時有小波動，但馬上回歸正常。電機在達到額定轉速后也能馬上調整到穩定狀態。

圖10是定子dq軸電流波形圖。從圖中可以看出，d軸電流在起動時會有大的波動，而后在零值附近波動。d軸電流在起動時的波動主要是由于起動時角度估算的誤差造成。q軸電流在起動之初也會有波動，但馬上歸于穩定，并且在轉矩變化時，也能快速達到穩定狀態。

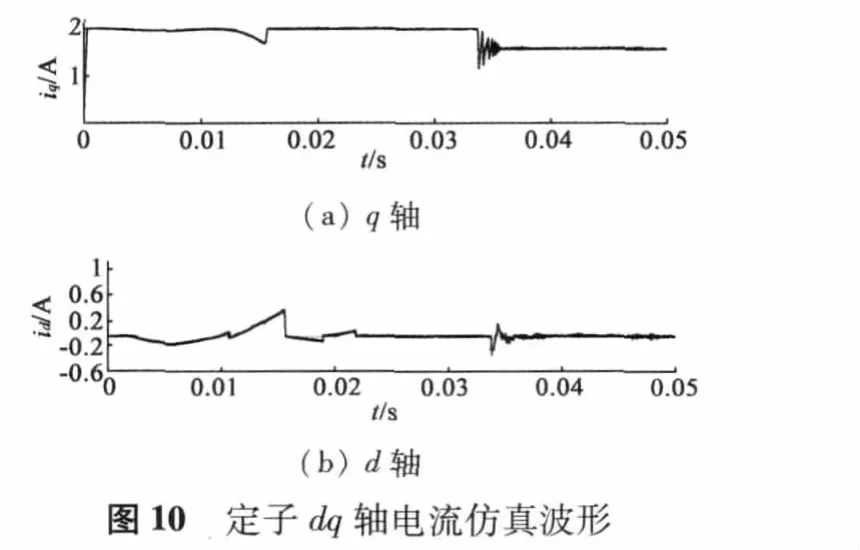
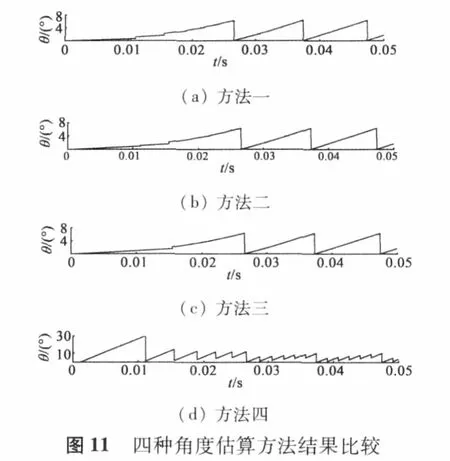
圖11是在指令速度為3000 r/min時的四種角度估算方法的波形。從上到下依次為第一種轉子角度估算方法到第四種角度估算方法。從圖中可以看出隨著算法的改進，轉子角度估算得到明顯改進，角度波形趨于平滑。同時可以看出，第四種角度估算方法在高速時不適用，但在低速時效果不錯，如圖12所示。圖12(a)是通過第四種方法估算得到的轉子角度曲線，圖12(b)是實際的轉子角度曲線。指令轉速為60 r/min，從圖中可以看出，角度估算曲線快速趨于穩定，電機運轉性能穩定。

6 結 語

本文分析了低成本的永磁同步電動機矢量控制系統的組成原理。重點介紹了id=0的永磁同步電動機控制策略，基于開關型霍爾的幾種永磁同步電動機轉子角度估算方法，并在MATLAB/Simulink環境下搭建了永磁同步電動機矢量控制仿真模型來驗證以上方法的可行性。通過運行仿真模型得到了基于以上方法的永磁同步電動機的運行性能。仿真實驗結論表明:仿真波形符合理論分析，整個系統運行穩定且具有良好的靜、動態性能。可以看出id=0的控制策略有如下特點:

(1)id=0使得β=90°電角度，無去磁效應，定子電流全部用來輸出轉矩。因此控制簡單，性能好、效率高。

(2)當負載增加時，定子電壓矢量和定子電流矢量的夾角將增大，永磁同步電動機功率因數降低，逆變器容量的要求也增高。因此適用于小容量的永磁同步電動機控制系統。

幾種轉子角度估算方法各有優缺點，總體隨著算法復雜程度的增加，估算得到的轉子角度精度得到增強，但在實際應用中會大大增加控制器的開銷。第四種方法最為簡單，但它只能用于低轉速。在實際的應用中可根據不同的要求做出選擇或者綜合幾種方法以獲得最佳效果。

［1］王成元，夏加寬.楊俊友，等.電機現代控制技術［M］.北京:機械工業出版社，2006.

［2］Cordne K A，Sudhaff S D.A Hybrid observer for High Performance Brushless DC Motor Drives［C］//IEEE Transactions on Energy conversion，1996，11(2):318 －323.

［3］Bu J，XU L，Sebastan T.Near－ zero speed performance enhancement of PM synchronous machines assisted by low cost Hall effect sensors［J］.Applied Power Electronics Conference and Exposition，1998，1:64 －68.

［4］曾風平，鄭成勇，章躍進.基于開關型霍爾位置傳感器的永磁同步電機正弦波驅動［J］.微特電機，2010(8):56－58.

［5］房森林，章躍進.基于離散位置信號的永磁同步電動機空間矢量控制［J］.微特電機，2010(7):51－53.

［6］董窈窈.采用低分辨率位置傳感器的正弦波永磁同步電機控制系統［D］.濟南:山東大學，2007.

［7］Jia Gui－ xi，Zhao Hui－ chao，Shao Hong － jun.Simulation research on PMSM vector control system based on SVPWM［C］//2010 International Conference on Electrical and Control Engineering，2010:1936 －1940.

［8］王爭光，金建勛，郭有光，等.基于SVPWM的永磁同步電機控制系統模型仿真［C］//Proceedings of the 27th Chinese Control Conference.Kunming，Yunnan，China，2008:724 －728.

［9］高靜.直驅式滾筒洗衣機用PMSM驅動系統關鍵技術研究［D］.哈爾濱:哈爾濱工業大學，2010.