修改的BWRS狀態方程
苑偉民
(中國石化天然氣分公司廣西液化天然氣工程項目部,廣西北海 536000)
0 引言
在天然氣工程中,在進行輸氣管道水力熱力計算時需要計算天然氣的熱物性參數,如密度、壓縮因子、焓、熵、定壓熱容、熱容比、焦耳—湯姆遜系數等,這就需要用到狀態方程,并且隨著管道仿真技術的發展,對于模型精度的要求也越來越高。準確計算流體的屬性和建立準確的熱力學模型需要準確的狀態方程[1]。
由于BWRS狀態方程可用于氣體和液體計算,其方程系數可由公式算得,并且有適用于很多烴類的混合規則;因此,在高密度或者含有凝液的管道仿真中BWRS是使用最廣的狀態方程[2]。但是,Staring給出了18種常見組分間的二元交互作用系數Kij數據,對于天然氣多樣化的組分還是顯得有些少,有必要增添常用組分及其二元交互作用系數。其次,BWRS方程中所采用的密度單位為kmol/m3[3-8],而在國際單位制中[9],密度的單位采用kg/m3;同時在天然氣穩態模擬及其他工藝計算中,需要用到BWRS方程的偏微分項,其單位制同樣需要轉換,如果直接修改方程系數,使其各個參數都統一為國際單位制,這樣用BWRS方程來求解其他參數時就會很方便。如何對其中各參數的單位進行統一,文獻 [3-8]都沒有給予說明,并且這些文獻中同一物性參數存在多種單位制,沒有統一的單位制[10]。再次,由于BWRS狀態方程是關于密度的隱式方程,如何精確并且快捷地求解該超越方程也是值得關注的。
為此,給出了改寫的BWRS狀態方程——MBWRS狀態方程。
1 Benedict-Webb-Rubin-Starling (BWRS) 狀態方程
BWRS方程是通過修正BWR方程而得到的,它保留了BWR方程中與密度關聯的系數項,改變了與溫度關聯的系數項。BWRS方程包含了計算輕烴組分的系數,決定烴類混合物氣體系數的混合規則,因此可以用于熱力學性質計算和氣液平衡計算。
BWRS狀態方程是一個多參數狀態方程,其基本形式[3-8]為:
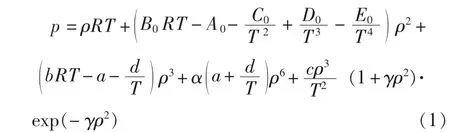
式中p——系統壓力/kPa;
ρ——氣相或液相的密度/(kmol/m3);
R——通用氣體常數,8.314 3 kJ/(kmol·K);
T——系統溫度/K。
方程中的 11 個參數 A0,B0, C0, D0, E0,a,b,c,d,α,γ必須通過大量的實驗得到。
2 改寫的BWRS狀態方程 (MBWRS狀態方程)
2.1 因次和諧
在工程中許多實際問題目前尚不能用數學分析求解。有時雖然導出偏微分方程,但它是非線性的,亦常難于得到精確解。這就不得不借助于實驗,此即經驗公式的來源。經驗公式能近似地在一定范圍內符合實際情況;經驗公式的導出又和涉及某一物理現象的各種參數及其合理排列有關。借助于因次分析,把控制物理現象的參數化為無因次群,這為實驗數據處理提供極大方便。
對于一個物理現象所包含的各物理量間的函數關系,如果選用一定的單位制,則其關系的函數式就確定了。若改變單位制則函數關系可能受影響,要保持函數關系不變,就必須具有特殊函數關系的結構形式。有物理意義的代數表達式或完整的物理方程是因次和諧的,或稱齊次的。一個方程如果因次上齊次,則方程的表達式不隨基本單位的改變而改變[11]。
下面給出將BWRS狀態方程改寫為無因次方程的轉化公式。
2.2 BWRS方程的改寫
將BWRS方程各參數改寫為如表1所示的形式:

表1 BWRS方程中各參數的改寫
11個參數的關聯式仍保持不變,混合規則亦保持不變。于是BWRS方程轉化為:
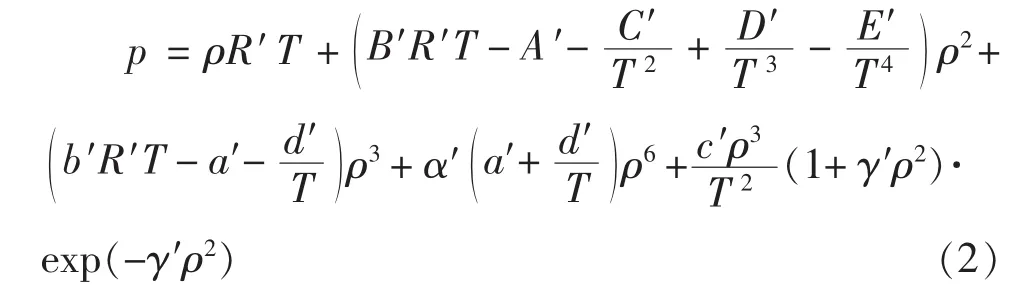
式中p——系統壓力,其因次為ML-1T-2;
T——系統溫度,其因次為Θ;
ρ——氣相的密度,其因次為ML-3;
R′——氣體常數,其因次為L2T-2Θ-1;
W——平均分子量。
上述因次的物理意義如下:長度的因次為L,質量的因次為M,時間的因次為T,溫度的因次為Θ[11-12]。通過上述處理發現,方程中11個參數的量綱并未轉換為1,但是,可以發現,上述公式中的參數已經不受單位制限制,由π定理可知,此時該函數關系為無因次的函數關系。
將方程 (2)中的參數改寫如下,其意義仍為修改過的BWRS方程:
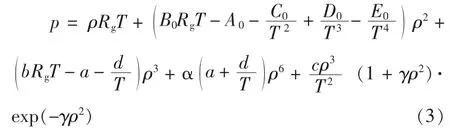
式中Rg——氣體常數,其因次為L2T-2Θ-1。
2.3 二元交互作用系數的改進
Staring給出了18種常見組分間的Kij數據,但是對于天然氣多樣化的組分還是顯得有些少,在參考商業軟件的基礎上,增添了一些常見組分,包括了在內的25個組分,見表2,為準確地求得天然氣的物性參數提供了有力的保障。
3 方程的求解
Starling提供了純物質的臨界性質和普適化系數。一旦知道了對于流體所附加的系數值 (臨界參數、分子量等),所有的狀態參數都可以用己知的狀態來計算。但是,很多流體模型通過流動方程計算壓力和溫度,用狀態方程求解密度或者壓縮因子[2]。由于BWRS方程中關于密度的關系式是隱式的,需要通過迭代方法來計算,使得大型管網中的密度或者壓縮因子計算需要消耗大量的時間[13],用弦截法求解簡單、快捷、精確。
3.1 密度的求解
將已知壓力p、溫度T代入式 (3)進行計算,求得氣體密度ρ。為方便求解,將式 (3)改寫為如下形式,并用弦截法求解[14]。
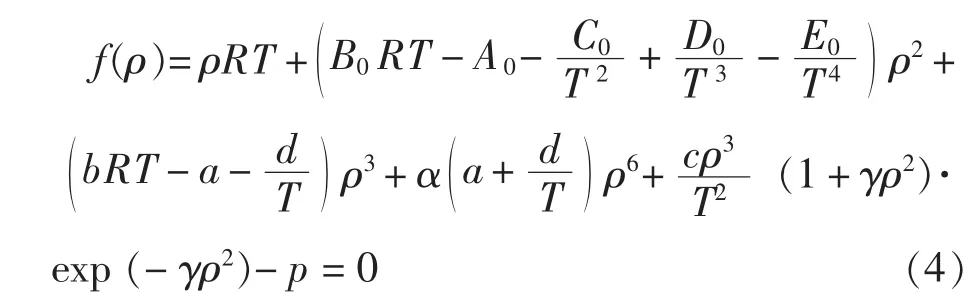
弦截法迭代公式為:
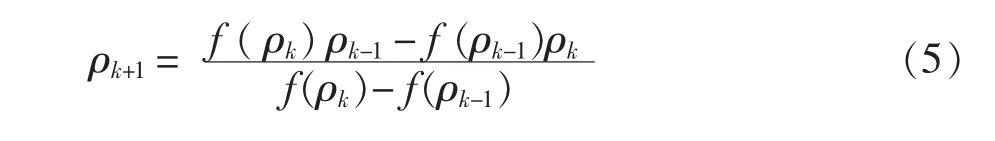
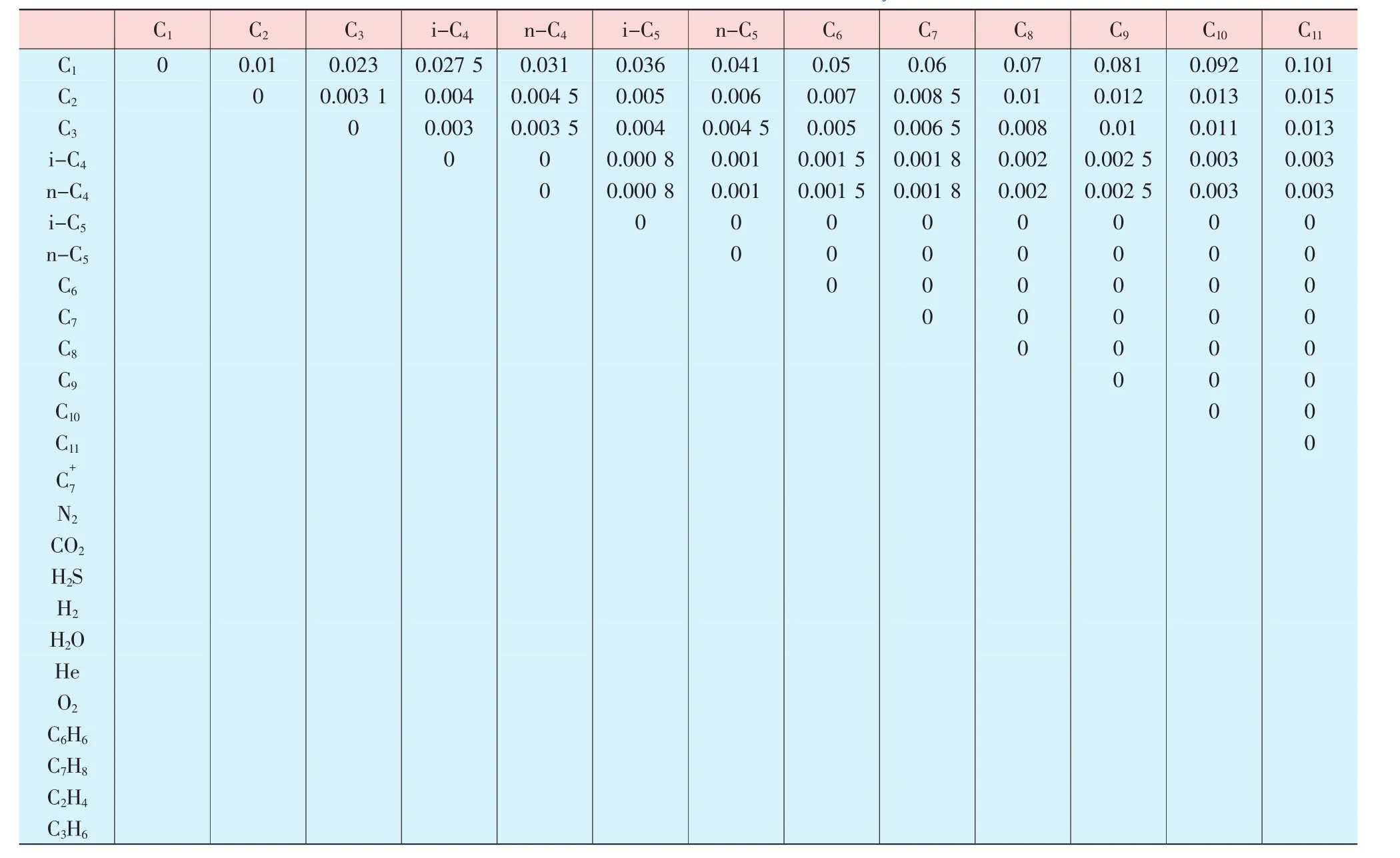
表2 BWRS修改模型中的二元交互作用系數Kij(待續)
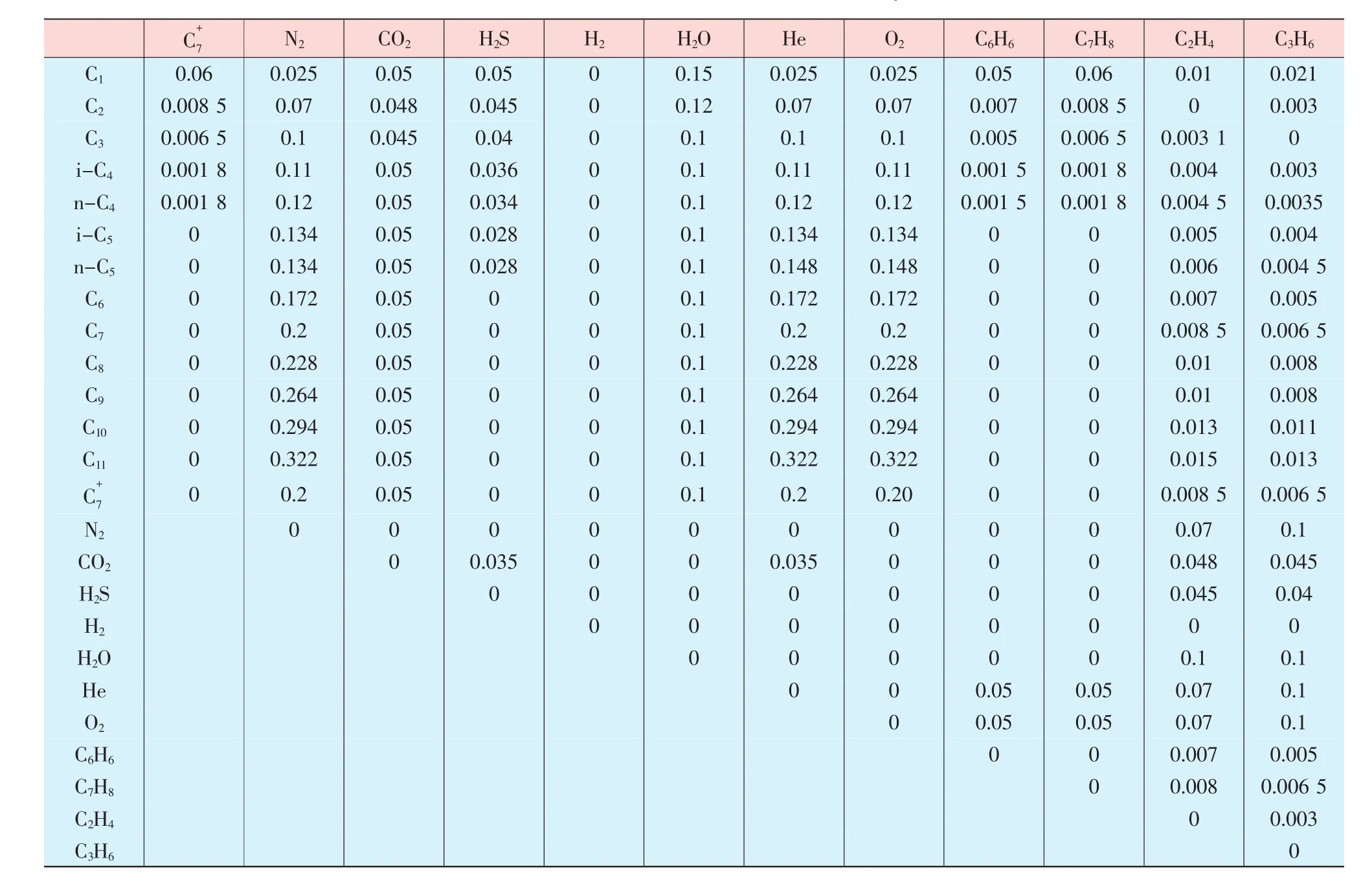
表2 BWRS修改模型中的二元交互作用系數Kij(續)
弦截法求解需設兩個初值。
求解氣相時:可設ρ1=0,ρ2=
求解液相時:當混合物的偏心因子ωm≤0.24時, ρ1=40.0 kmol/m3(40 mol/L,kg/m3), ρ2=38.0 kmol/m3(38.0 mol/L, kg/m3); 當混合物的偏心因子 ωm> 0.24時, ρ1=20.0 kmol/m3(20 mol/L,kg/m3), ρ2=18.0 kmol/m3(18.0 mol/L, kg/m3)。
迭代到|ρk-ρk-1|≤ε為止,取ε=10-6時,一般迭代次數在6次左右即能收斂。
3.2 壓縮因子的求解
當求解出密度后,壓縮因子可用下式計算:
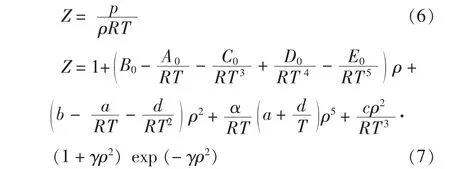
式 (6)和式 (7)計算結果并無差別,推薦使用式 (6), 便于計算[15]。
4 結論
(1)對BWRS狀態方程的11個參數進行了改寫,將BWRS方程的函數關系轉化為無因次的函數關系。使用MBWRS狀態方程,可以引入任何一套國際單位制和非國際單位制,計算過程無需單位制轉換,避免了管道模擬模型或者其他計算中單位制換算帶來的累積誤差。
(2)BWRS方程的修正中還包括:引入BWRS新的研究成果,添加了常用組分及其二元交互作用系數。彌補了BWRS狀態方程中沒有的組分,為更為準確地求得天然氣的物性參數提供了有力的保障。
[1]Modisette J L.Equation of State Tutorial[A].PSIG Annual Meeting,2001[C].Salt Lake City:PSIG,2001.
[2]苑偉民,青青,袁宗明,等.輸氣管道模擬狀態方程[J].油氣儲運,2010,29(3):194-196.
[3]李長俊,汪玉春,陳祖澤,等.天然氣管道輸送[M].北京:石油工業出版社,2000.
[4]郭天民,閻煒,濮蕓輝.多元氣液平衡和精餾[M].北京:石油工業出版社,2002.
[5]袁宗明,謝英,梁光川.城市配氣[M].北京:石油工業出版社,2004.
[6]姚光鎮.輸氣管道設計與管理[M].山東:石油大學出版社,1991.
[7]吳玉國,陳保東.BWRS方程在天然氣物性計算中的應用[J].油氣儲運,2003,22(10): 16-21.
[8]童景山.流體的熱物理性質[M].北京:中國石化出版社,1996.
[9]Gas Processors Suppliers Association.Engineering Data Book[M].Tulsa:GPSA,2004.
[10]苑偉民,孫嘯,賀三,等.BWRS方程中參數單位制的討論[J].長江大學學報(自然科學版), 2008,5(3):179-180.
[11]袁恩熙.工程流體力學[M].北京:石油工業出版社,2002.97-105.
[12]趙漢中.工程流體力學 (I)[M].武漢:華中科技大學出版社,2005.154-161.
[13]苑偉民,袁宗明,賀三,等.輸氣管網穩態模擬方法研究[J].油氣儲運,2009,28(10):34-38.
[14]苑偉民,賀三,袁宗明,等.求解BWRS方程中密度根的數值方法[J].天然氣與石油,2009,27(1):4-6.
[15]苑偉民,賀三,袁宗明,等.求解BWRS方程中壓縮因子的數值方法[J].管道技術與設備,2009,16(3):14-16.

