利用尋位信息的自由曲面在線測(cè)量路徑規(guī)劃方法*

邵 偉 郭俊杰

（①西安理工大學(xué)，陜西西安710048;②西安交通大學(xué)，陜西 西安 710049）

隨著航天、航空、造船、汽車(chē)等工業(yè)的飛速發(fā)展，使得自由曲面零件在現(xiàn)代工業(yè)中得到了越來(lái)越廣泛的應(yīng)用，并且對(duì)產(chǎn)品性能、外形等方面的要求越來(lái)越高，而對(duì)該類(lèi)工件的曲面建模、數(shù)控加工和產(chǎn)品表面質(zhì)量評(píng)定都離不開(kāi)對(duì)自由曲面工件幾何形狀的測(cè)量。其測(cè)量精度和效率直接影響到后續(xù)處理的質(zhì)量和效率［1］。為了有效地實(shí)現(xiàn)對(duì)自由曲面工件的在線測(cè)量，就有必要對(duì)其進(jìn)行合理的測(cè)量路徑規(guī)劃。測(cè)量路徑規(guī)劃是確定測(cè)頭在測(cè)量空間的運(yùn)動(dòng)軌跡，即工件上測(cè)量點(diǎn)的分布及其測(cè)量順序。測(cè)量時(shí)一般以面作為最小的測(cè)量單位，要求測(cè)量完一個(gè)面后，才能進(jìn)行下一個(gè)面的測(cè)量。測(cè)量路徑規(guī)劃的好壞直接影響著測(cè)量效率和重構(gòu)曲面的精度。測(cè)點(diǎn)數(shù)目的多少受到被測(cè)物體尺寸大小、檢測(cè)公差的精度要求和測(cè)量機(jī)測(cè)量精度大小的綜合影響。被測(cè)物尺寸大時(shí)，應(yīng)進(jìn)行多測(cè)點(diǎn)測(cè)量，尺寸小時(shí)則可進(jìn)行少測(cè)點(diǎn)測(cè)量;測(cè)量的精度要求高時(shí)，測(cè)量的點(diǎn)數(shù)就應(yīng)該多，反之則少;測(cè)量機(jī)的測(cè)量精度高時(shí)，測(cè)量相同物體的測(cè)點(diǎn)的數(shù)目可以少，精度低時(shí)就要多。在上述3項(xiàng)一定的情況下，就要對(duì)測(cè)量點(diǎn)的分布進(jìn)行研究，使得測(cè)量點(diǎn)分布的疏密盡可能地隨曲面曲率的變化而變化，同時(shí)減小測(cè)量機(jī)自身誤差的影響，使測(cè)量結(jié)果盡可能地反映工件的實(shí)際形狀，從而在滿足精度要求的前提下使測(cè)點(diǎn)的數(shù)目盡可能的少，滿足在線測(cè)量高效率的要求［2－6］。

已知CAD模型的大型曲面測(cè)量規(guī)劃方法是在設(shè)計(jì)基準(zhǔn)坐標(biāo)系下根據(jù)加工精度要求確定測(cè)點(diǎn)數(shù)和測(cè)點(diǎn)分布，以及對(duì)應(yīng)理論模型上的點(diǎn)，由這些點(diǎn)指導(dǎo)測(cè)量機(jī)進(jìn)行測(cè)量，然后對(duì)加工機(jī)床進(jìn)行相應(yīng)的工藝指導(dǎo)，這就涉及到設(shè)計(jì)坐標(biāo)系、測(cè)量坐標(biāo)系、加工坐標(biāo)的統(tǒng)一，因此在測(cè)量路徑規(guī)劃中如何實(shí)現(xiàn)設(shè)計(jì)坐標(biāo)系、測(cè)量坐標(biāo)系、加工坐標(biāo)的統(tǒng)一對(duì)測(cè)量軌跡和加工軌跡的控制至關(guān)重要［7－8］。本文提出了一種基于工件尋位的方法，建立坐標(biāo)系之間的相互關(guān)系實(shí)現(xiàn)坐標(biāo)系的統(tǒng)一，其原理就是通過(guò)對(duì)工件上的特征點(diǎn)的測(cè)量來(lái)找出測(cè)量坐標(biāo)系相對(duì)設(shè)計(jì)坐標(biāo)系和加工坐標(biāo)的相對(duì)位置關(guān)系，保證測(cè)量過(guò)程中測(cè)頭的運(yùn)動(dòng)與工件的CAD模型規(guī)劃軌跡一致。因此本文采用一種基于曲面工件自動(dòng)尋位的坐標(biāo)系統(tǒng)一原則和測(cè)點(diǎn)布置于一體的測(cè)量路徑規(guī)劃方法。下面首先介紹基于曲面工件自動(dòng)尋位信息的坐標(biāo)系關(guān)系的建立。

1 基于自動(dòng)尋位信息的坐標(biāo)系關(guān)系的建立

坐標(biāo)系關(guān)系的建立就是要確定設(shè)計(jì)坐標(biāo)系、測(cè)量坐標(biāo)系、加工坐標(biāo)系的相互轉(zhuǎn)換關(guān)系，即轉(zhuǎn)換矩陣的求解，因此，建立曲面測(cè)量坐標(biāo)系與設(shè)計(jì)坐標(biāo)系和加工坐標(biāo)系之間的變換關(guān)系成為轉(zhuǎn)換矩陣的求解。針對(duì)CAD模型己知的待測(cè)大型曲面工件，可根據(jù)預(yù)先測(cè)量獲取的工件表面上少數(shù)測(cè)點(diǎn)的信息，通過(guò)一定的計(jì)算將其與CAD模型上對(duì)應(yīng)的點(diǎn)對(duì)齊，快速準(zhǔn)確地求解出工件的實(shí)際狀態(tài)（工件在測(cè)量機(jī)上的位置與姿態(tài)），即求解出測(cè)量坐標(biāo)系和設(shè)計(jì)坐標(biāo)系之間的真實(shí)關(guān)系。一般工件測(cè)量坐標(biāo)系和設(shè)計(jì)坐標(biāo)系之間的關(guān)系可用齊次變換矩陣T表示為

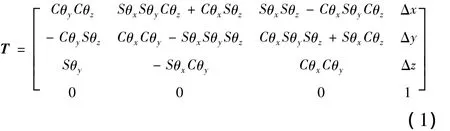
式中:Δx、Δy、Δz為測(cè)量坐標(biāo)系原點(diǎn)相對(duì)于設(shè)計(jì)坐標(biāo)系原點(diǎn)的平移量;θx、θy、θz分別為測(cè)量坐標(biāo)系繞設(shè)計(jì)坐標(biāo)系x、y、z軸的旋轉(zhuǎn)角度;S和C分別是sin和cos的縮寫(xiě)。

由于直接快速精確求解T是比較困難的，為此本文采用如下的方法［9－10］來(lái)對(duì)模型已知的待測(cè)大型工件進(jìn)行尋位信息提取。該方法具體步驟可描述如下:

（1）初始化——使變換矩陣T0為

其中（xc，yc，zc）為初始測(cè)點(diǎn)的質(zhì)心;并且初始化與測(cè)點(diǎn)（i=l，2，…，n;j=1，2，…，m）對(duì)應(yīng)的曲面上的理論點(diǎn)（i=l，2，…，n;j=1，2，…，m）。

（2）計(jì)算測(cè)點(diǎn)Pij與工件理論曲面間的偏差

（3）置k=k+l;

（4）確定測(cè)點(diǎn)Pij對(duì)應(yīng)的曲面上的理論點(diǎn)

由于測(cè)量坐標(biāo)系的測(cè)點(diǎn)相對(duì)工件理論曲面間距離的平方為

解方程組（5）求出所對(duì)應(yīng)的參變量u、v的取值，最后將u、v之值代入坐標(biāo)函數(shù)表達(dá)式，即可求出的坐標(biāo)值;

（1）進(jìn)行變換矩陣T更新得到Tk;

（2）求取變換后的測(cè)點(diǎn):

（3）計(jì)算與工件理論曲面間的偏差

2 基于尋位信息的測(cè)量路徑規(guī)劃算法

實(shí)現(xiàn)曲面工件尋位測(cè)量的關(guān)鍵，是按所獲得的工件尋位信息對(duì)測(cè)量過(guò)程進(jìn)行位姿自適應(yīng)控制。下面提出一種對(duì)已知曲面進(jìn)行測(cè)量的基于尋位信息的路徑軌劃方法。下面介紹算法的具體實(shí)現(xiàn)過(guò)程。

2.1 曲面工件的測(cè)點(diǎn)生成算法

如果對(duì)待測(cè)曲面工件的整個(gè)幾何形狀自適應(yīng)地進(jìn)行測(cè)點(diǎn)布置，將使得計(jì)算的工作量相當(dāng)大，在一定的精度條件下也完全沒(méi)必要。一種合理的解決辦法就是首先根據(jù)給定的精度要求，在曲面上自適應(yīng)生成檢測(cè)方向上的測(cè)量曲線，在避免漏檢的前提下盡可能減少測(cè)量曲線的數(shù)目;然后對(duì)每一條測(cè)量曲線按等步距進(jìn)行測(cè)點(diǎn)布置以生成曲面工件的測(cè)點(diǎn)。其中曲面工件的測(cè)量曲線自適應(yīng)生成就是根據(jù)待測(cè)曲面的具體幾何形狀自適應(yīng)地進(jìn)行測(cè)量曲線的布置，使測(cè)量曲線分布的疏密隨曲面曲率變化而變化，從而在滿足精度要求的前提下使測(cè)量曲線的數(shù)目盡可能地少，以提高測(cè)量的效率。如圖1所示，對(duì)應(yīng)于一定精度要求的測(cè)量曲線生成過(guò)程如下:

步驟1:檢測(cè)方向上測(cè)量曲線的分布。對(duì)于曲面:

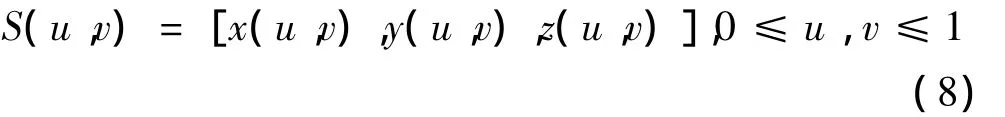
假設(shè)參數(shù)u方向（或v方向）為其檢測(cè)方向，并且沿該方向分布n條測(cè)量曲線，首先根據(jù)掃描間距用等參數(shù)方法進(jìn)行曲面離散（如圖1所示），得到各離散型值點(diǎn)Sij=S（ui，vj）（i=l，2，…，r;j=1，2，…，l）。接著，將該離散的曲面按u方向（或v方向）劃分成m個(gè)離散小曲面，m一般應(yīng)等于1/5～1/2倍的測(cè)量曲線數(shù)n。

接著，對(duì)每個(gè)離散小曲面中各點(diǎn)進(jìn)行曲率數(shù)值的計(jì)算。根據(jù)歐拉公式，設(shè){e1，e2}是曲面在任一P點(diǎn)的兩個(gè)彼此正交的主方向單位向量，對(duì)應(yīng)的主曲率為k1、k2，則在P點(diǎn)沿任意一個(gè)單位切向量e=e1cosθ+e2sinθ的法曲率為

從式（9）不難看出，主方向正是法曲率取極值的方向，而主曲率正好是法曲率極值，即如果k1≥k2，則在曲面上在該點(diǎn)沿任意一個(gè)切方向的法曲率滿足不等式

在實(shí)際應(yīng)用中，取曲面上P點(diǎn)的絕對(duì)曲率

反映曲面上該點(diǎn)的彎曲程度。其中，主曲率k1、k2分別為曲面在一點(diǎn)處的最小、最大曲率。進(jìn)而通過(guò)式（11）可計(jì)算出各離散小曲面上各點(diǎn)的曲率測(cè)度及其最大最小值。

然后，對(duì)每個(gè)小曲面采用均勻分布的方法進(jìn)行測(cè)量曲線的分布，分布曲線數(shù)ni為

到此，就完成了沿曲面u參數(shù)方向（或v方向）n條測(cè)量曲線的分布，并將這n條測(cè)量曲線作為當(dāng)前測(cè)量曲線集C（n）。

步驟2:由上面確定的n條測(cè)量曲線重構(gòu)CAD模型得到一個(gè)替代曲面模型S*。

步驟3:計(jì)算曲面模型S*與CAD模型之間的偏差Δ。設(shè)ε為測(cè)量精度和工序能力共同確定的精度要求，如果

不成立，并且n＜N（N為預(yù)先指定的正數(shù)），則令n=n+1，重復(fù)上述過(guò)程直至式（13）成立。于是可取C=C（n），由該方法所生成的測(cè)量曲線集可以滿足對(duì)曲面檢測(cè)測(cè)量曲線數(shù)目和自適應(yīng)分布的要求，以便對(duì)曲面的形狀誤差做出準(zhǔn)確評(píng)定。

2.2 幾何信息變換和測(cè)量路徑的生成

為實(shí)現(xiàn)對(duì)模型已知的大型曲面工件進(jìn)行測(cè)量，需將待測(cè)曲面工件的有關(guān)幾何信息從設(shè)計(jì)坐標(biāo)系變換到測(cè)量坐標(biāo)系。因此，在求得齊次變換矩陣T后，可用T－1對(duì)由曲面CAD模型生成的測(cè)點(diǎn)數(shù)據(jù)Qij進(jìn)行變換，即將CAD模型面的測(cè)點(diǎn)變換到測(cè)量坐標(biāo)系中，其表達(dá)式為

遍歷上述測(cè)點(diǎn)數(shù)據(jù)即可得到的曲面測(cè)量路徑。

3 仿真與實(shí)驗(yàn)

為了驗(yàn)證上述算法的有效性，進(jìn)行了多次仿真實(shí)驗(yàn)。仿真實(shí)驗(yàn)之一所用工件的CAD曲面輪廓如圖2所示。在一定的精度要求下，利用測(cè)量曲線自適應(yīng)布置算法進(jìn)行測(cè)量曲線自適應(yīng)分布的結(jié)果如圖3所示。由圖中不難發(fā)現(xiàn)測(cè)量曲線的分布在曲面曲率大的地方分布得密，而曲率小的地方分布得疏。

對(duì)于該工件如按常規(guī)方法進(jìn)行測(cè)量，則由于定位不準(zhǔn)，使得工件的實(shí)際測(cè)點(diǎn)與理論測(cè)點(diǎn)產(chǎn)生較大的誤差，此時(shí)測(cè)量坐標(biāo)系相對(duì)于設(shè)計(jì)坐標(biāo)系的位移和旋轉(zhuǎn)量如表1第二列所示。為消除這種誤差，采用尋位控制方法對(duì)測(cè)量過(guò)程進(jìn)行控制。為此先在工件表面上確定一定數(shù)量的測(cè)量點(diǎn)（本次實(shí)驗(yàn)為10個(gè)），并取得這些點(diǎn)的坐標(biāo)值，將這些測(cè)點(diǎn)的數(shù)據(jù)輸入控制計(jì)算機(jī)，運(yùn)行該機(jī)中的工件定位控制軟件，經(jīng)計(jì)算出被定位工件的狀態(tài)估計(jì)值即尋位計(jì)算值如表1最后一列所示。

用所求得齊次變換矩陣T后，將工件曲面的自適應(yīng)測(cè)點(diǎn)從設(shè)計(jì)坐標(biāo)系變換到測(cè)量坐標(biāo)系，使設(shè)計(jì)坐標(biāo)系和測(cè)量坐標(biāo)系趨于一致，此時(shí)最大誤差為0.008 5 mm。這說(shuō)明該尋位測(cè)量方法具有較高的精度，可以滿足曲面工件的測(cè)量要求。

表1 工件狀態(tài)

圖4為以自適應(yīng)采樣路徑規(guī)劃得到的最小測(cè)量曲線行間距（5.236 1 mm）進(jìn)行等行距測(cè)量曲線布置的結(jié)果，共有19條測(cè)量曲線。由此可見(jiàn)，和本文采用的測(cè)量路徑規(guī)劃方法相比，在相同的測(cè)量效果下，本文采用的測(cè)量路徑規(guī)劃得到的測(cè)量曲線數(shù)顯著減少，可以較好地提高采樣效率。

圖5為以自適應(yīng)采樣路徑規(guī)劃得到的某工件測(cè)量曲線布置的結(jié)果和實(shí)際測(cè)量曲面的誤差分布圖，其結(jié)果和實(shí)際基本相符。由此可見(jiàn)，本文采用的測(cè)量路徑規(guī)劃方法在相同的測(cè)量效果下，可以較好地提高采樣效率。

4 結(jié)語(yǔ)

提出了一種基于尋位信息的大型曲面工件的設(shè)計(jì)坐標(biāo)系、測(cè)量坐標(biāo)系、加工坐標(biāo)的統(tǒng)一方法，在此基礎(chǔ)上實(shí)現(xiàn)測(cè)量路徑規(guī)劃，實(shí)現(xiàn)測(cè)量過(guò)程中對(duì)測(cè)點(diǎn)的布置。該方法根據(jù)待測(cè)曲面上相鄰子曲面內(nèi)測(cè)點(diǎn)的平均曲率為判據(jù)來(lái)進(jìn)行測(cè)量曲線的自適應(yīng)分布，可以保證測(cè)量曲線分布的疏密隨曲面曲率變化而變化，以提高測(cè)量的效率;接著對(duì)每一條測(cè)量曲線按等步距進(jìn)行測(cè)點(diǎn)布置以生成曲面工件的測(cè)點(diǎn)。然后基于尋位信息，將測(cè)點(diǎn)從設(shè)計(jì)坐標(biāo)系變換到測(cè)量坐標(biāo)系。仿正和實(shí)例表明，上述方法具有算法簡(jiǎn)潔、采樣精度容易控制的特點(diǎn)，在相同采樣精度下可顯著提高在線測(cè)量效率，滿足在線測(cè)量高效率的要求，有效提高加工質(zhì)量。

［1］裘祖榮，石照耀，李巖.精密測(cè)試技術(shù)展望［J］.中國(guó)機(jī)械工程，2010，46（14）:1－11.

［2］靳宣強(qiáng)，姜秀麗，胡禎，等.淺析數(shù)控機(jī)床在線檢測(cè)技術(shù)［J］.現(xiàn)代制造技術(shù)與裝備，2009（3）:40－42.

［3］Seokbae S，Seungman K，Kwan H L.Path planning of multi－patched freeform surfaces for laser scaning［J］.Int.J.Adv.Manuf.Technol.，vol.224，pp.424 －435，2003.

［4］趙吉賓，劉偉軍，孫玉文，等.自由曲面測(cè)量點(diǎn)云數(shù)據(jù)的建模方法研究［J］.儀器儀表學(xué)報(bào)，2006，27（19）:1044 －1047.

［5］劉強(qiáng)，李冬茹.國(guó)產(chǎn)數(shù)控機(jī)床及其關(guān)鍵技術(shù)發(fā)展及展望［J］.航空制造技術(shù)，2010（10）:26－30.

［6］趙振宇，張萌，周后明.最短路優(yōu)化的復(fù)雜型腔刀具軌跡規(guī)劃算法［J］.制造技術(shù)與機(jī)床，2009（1）:39 －42.

［7］石為人，王楷.基于Floyd算法的移動(dòng)機(jī)器人最短路徑規(guī)劃研究［J］.儀器儀表學(xué)報(bào)，2009，30（10）:2088 －2092.

［8］梁義，陳建軍，陳立崗，等.幾何自適應(yīng)參數(shù)曲面網(wǎng)格生成［J］.計(jì)算機(jī)輔助設(shè)計(jì)與圖形學(xué)學(xué)報(bào)，2010，22（2）:327－335.

［9］紀(jì)小剛，龔光榮.三坐標(biāo)測(cè)量機(jī)中基于遺傳算法的多特征測(cè)量路徑規(guī)劃研究［J］.兵工學(xué)報(bào)，2005，26（3）:392 －396.

［10］徐金亭，孫玉文，劉偉軍.復(fù)雜曲面加工檢測(cè)中的精確定位方法［J］.中國(guó)機(jī)械工程，2007，43（6）:175 －179.