一種基于GA－SA－TS算法的車間調度方法的研究

劉紅軍 趙 帥 趙 雷

(①沈陽理工大學機械工程學院，遼寧沈陽 110159;②北京城建設計研究總院有限責任公司，北京 100037)

隨著科學技術的不斷發展，社會節奏的不斷加快，將科學的管理調度技術與車間生產調度緊密結合起來，在現代加工車間中已得到了普遍的應用。而如何將科學技術與車間生產調度更好地融合到一起，成為了當今科學領域普遍重視的問題。車間調度問題實質上就是研究在已有的資源條件和一定的約束條件下，對加工任務進行加工時間、機器、順序等的合理分配，從而使生產加工達到最優化的狀態。

本文針對遺傳算法的局部搜索能力差，易限于局部最優等缺點，提出了一種適用于車間調度研究中的混合遺傳算法(GA－SA－TS)，即將模擬退火算法、禁忌搜索算法與遺傳算法混合使用。該算法的核心在于:在遺傳算法的交叉機制中引入模擬退火算法的思想，形成模擬退火－交叉機制，從而避免了遺傳算法本身易早熟的缺陷。在變異機制中使用禁忌搜索算法的思想，形成禁忌搜索－變異機制，以此解決遺傳算法變異壓力問題。通過這些方面的改進，提高了遺傳算法的優化效率。

1 車間調度問題的描述

車間調度問題就是研究N(N1，N2，…，NN)個工件在M(M1，M2，…，MM)臺機器上進行加工，每個工件具有一定數量的工序J(J1，J2，…，JJ)，每道工序可以在若干臺機器上加工，加工的過程按照工件的工藝順序完成。工件在加工的過程中要遵循以下約束:

(1)每臺機器在每個時刻只能加工一個工件的一道工序;

(2)每道工序只能被一臺機器加工;

(3)每個工件按給定的工藝路線和指定的次序在機器上進行加工;

(4)每個工件在每臺機器上開始加工后不可停止，直到完成該道工序的加工;

(5)每個工件只能在上道工序加工完成后才能開始下一道工序的加工［1－2］。

2 改進的遺傳算法

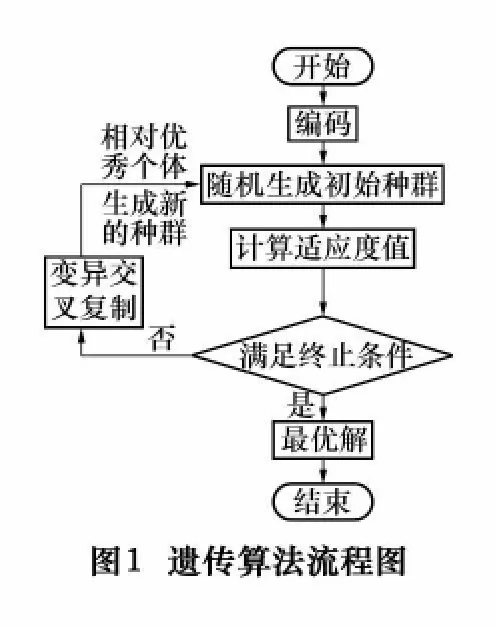
遺傳算法［3］(GA －Genetic Algorithms)主要是借鑒了生物進化過程中“適者生存”的規律，并將算法的整個過程都與生物進化過程中的各種概念對應起來，例如:遺傳算法中的解稱為個體，算法中對解進行的編碼稱為染色體等。圖1即為遺傳算法的流程圖。

模擬退火算法(SASimulated Annealing)是局部搜索算法的擴展，是以一定的接受概率選擇鄰域中的較優值，從而使SA成為一個全局最優算法。

禁忌搜索算法［4－5］(TS － Tabu Search)也是局部鄰域搜索算法的推廣。它的特點是采用了禁忌技術，即禁止重復前面的工作，從而跳出局部最優。

本文提出的混合遺傳算法(GA－SA－TS)，就是基于遺傳算法的整體流程，在其交叉機制中引入模擬退火算法的思想，在變異機制中引入禁忌搜索算法的思想。從而改善遺傳算法的局部搜索能力差的特點，進一步提高了優化的質量，彌補單一遺傳算法在優化方面的不足，達到取長補短的作用。

2.1 編碼方式

運用到車間調度系統中的編碼方式有:基于“串”的編碼、基于位置“列表”的編碼、基于工序的編碼、基于工件的編碼、基于偏好列表的編碼、基于優先規則的編碼、基于機器的編碼和基于完成時間的編碼等。針對車間調度的實際情況，本文選擇的是基于工件的編碼方式。這種編碼方式把調度編碼為工序的序列，每個基因代表一道工序。一般采用自然數來命名工序。由于基于工序的編碼方式本身就能滿足車間作業調度問題中的占用約束和順序約束的關系，因此該編碼方式常用于車間作業調度問題中。

2.2 適應度函數

遺傳算法中，主要就是依靠對各染色體的適應度函數的數值來確定染色體的優劣。因而適應度函數的確定對于優化過程起著至關重要的作用。適應度值高的染色體被保留操作的幾率就高，反之就低。本文將工件的加工時間作為調度的評定標準，即加工完成的時間越少越好，所以可視車間調度問題為最小值問題。根據適應度函數的種類，確定其適應度函數為

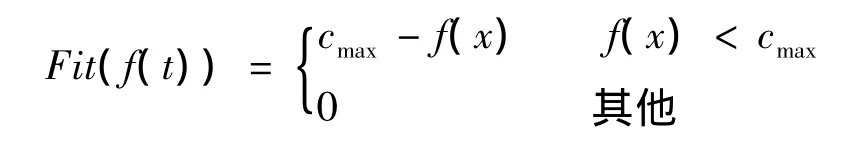
式中，cmax為一個適當的相對比較大的數，是f(x)的最大值估計［3］。

2.3 選擇操作

選擇操作是在群體中選擇生命力強的個體產生新的群體的過程。通過對每條染色體進行選擇概率的計算，選擇概率較高的個體被保留下來遺傳到下一代進行操作的概率就高，反之就低。選擇操作算子包括輪盤賭選擇、隨機競爭選擇、最佳保留選擇、無回放隨機選擇、確定性選擇、柔性分段選擇、均勻排序、穩態復制、復制評價等。本文選擇最佳保留選擇算子進行選擇操作，因為這種算子能夠保證迭代終止結果為歷代最高適應度個體。選擇操作的基本流程為:

(1)計算出個每條染色體所對應的適應度函數值fi;

(2)將各條染色體按照計算出的fi進行由高到低排序;

(3)按照選擇概率，從排序好的染色體群中按由高到低的順序選擇出n條染色體，并將這n條染色體完整的復制到下一代群體中。

2.4 模擬退火－交叉

本文通過對模擬退火算法的研究，提出一種模擬退火－交叉機制。所謂模擬退火－交叉，就是在遺傳算法的交叉機制中引入模擬退火算法的思想完成遺傳算法中的交叉操作。而模擬退火算法之所以成為全局尋優算法，是因為其采用了Metropolis［6］準則。該準則也被稱為接受準則，其內容為:

接受概率計算公式為

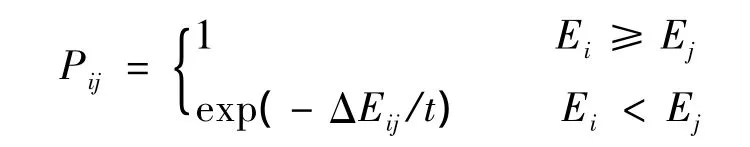
設初始狀態為i，該狀態的能量為Ei，然后從i的鄰域N(i)中隨機選一個新狀態j，新狀態的能量為Ej。如果Ei≥Ej，那么接受當前狀態i為新狀態;如果Ei＜Ej，則隨機產生一個數 ζ∈(0，1)，如果 ζ＜Pij，就以j取代i成為當前狀態。再重復以上新狀態的產生過程，直到系統趨于能量較低的平衡狀態。

本文提出的模擬退火－交叉機制就是借鑒了以上的思想，其具體操作流程如下:

Step1:令t0=k·Δ0(t0為模擬退火算法中的初始溫度，k為充分大的數，可選取k=10，20，100，…，Δ0=max{f(i)|i∈D}－ min{f(i)|i∈D})。

Step2:從區域D中選取兩條染色體 father1，father2。

Step3:判斷是否滿足終止條件(終止條件可以分為零度法，循環總數控制法，基于不改進規則的控制法，接受概率控制法，鄰域法，Lundy和Mees法，Aarts和van Laarhoven法等［7］。本文選擇循環總數控制法，即給定一個溫度下降次數K，當溫度迭代次數達到該值時，停止運算)，若滿足則退出交叉操作，輸出結果，否則轉至Step4。

Step4:對染色體father1、father2進行交叉操作，產生新的染色體son1、son2。

Step5:計算染色體 father1、father2、son1、son2 的適應度值。

Step6:根據Metropolis準則判定son1是否替代father1，son2是否替代 father2。

Step7:計算退溫函數:tk=λ·tk－1(其中k＞0，0 ＜λ＜1，λ取值越接近1，溫度下降越慢，所以可以取λ=0.95，0.9，…)，轉至 Step3。

2.5 禁忌搜索－變異

采用了禁忌技術，是禁忌搜索算法的一大特點。所謂禁忌，就是禁止重復之前的工作。為了避免局部搜索過早陷入局部最優的缺點，禁忌搜索算法用一個禁忌表將已經到達過的局部最優點或者到達局部最優的過程記錄下來，以便在后面的搜索中不再或者有選擇地對禁忌表中的這些點進行搜索，從而跳出局部最優。禁忌搜索是在一個染色體所產生的鄰域中進行尋優搜索操作，其中鄰域中的染色體是否替代原有染色體，需要運用特赦準則(也稱為藐視準則)進行判定。特赦準則保證了搜索過程在全部候選解被禁或是有優于當前最優解的候選解(或狀態)被禁時，能夠釋放特定解(或狀態)，從而實現高效的全局優化搜索［8］。

本文通過對禁忌搜索算法的研究，提出一種禁忌搜索－變異機制，即在遺傳算法的變異機制中融入禁忌搜索的思想。

禁忌搜索－變異的操作流程如下:

Step1:選擇一組染色體進入禁忌搜索棧中等待操作。

Step2:從禁忌搜索棧中選出一條染色體A1，并令Abest=A1，將禁忌表中內容清零。

Step3:由A1產生N個候選解(x1、x2、x3、…、xi)，形成一個以A1為基礎的鄰域。

Step4:計算出Step3產生的鄰域中所有染色體的適應度函數f，然后根據特赦準則判定新產生的染色體是否替代原有染色體，成為Abest，本文設定的特赦準則為:

如果f(Abest)≥f(xi)，則Abest值不變，并同時將xi放入禁忌表中，禁忌長度設為L=n;如果f(Abest)＜f(xi)，則Abest=xi，同時將原來的Abest的值放入禁忌表中，禁忌長度設為L=n。

Step5:判定是否滿足終止條件(設定終止條件為:禁忌搜索次數n);如果滿足轉至 Step6，否則轉至Step3。

Step6:判定禁忌搜索棧中的染色體是否全部完成禁忌搜索－變異操作，如果是，轉至Step7，否則轉至Step2。

Step7:輸出禁忌搜索－變異操作的結果。

3 實際算例的仿真驗證

下面就GA－SA－TS混合遺傳算法的可操作性在某廠的加工車間進行了實際驗證。實際參數如表1所示。

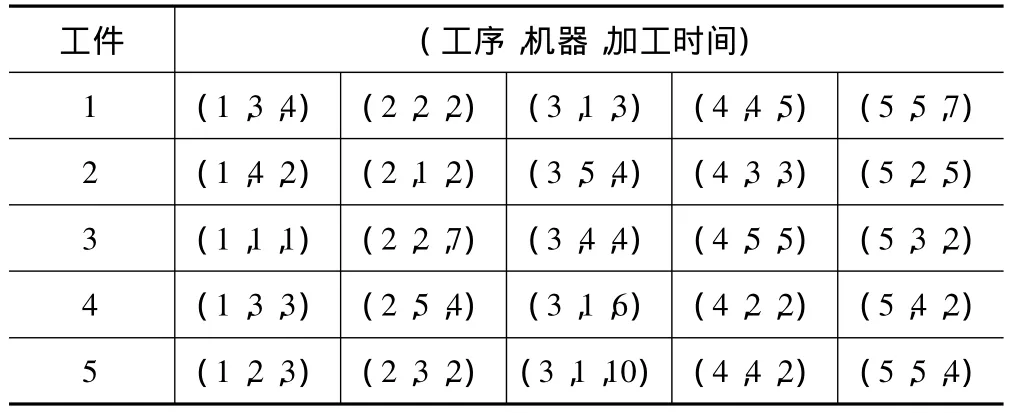
表1 工廠實際加工參數

通過MATLAB實際仿真，得到一條最優染色體為:

［5 2 5 3 1 3 4 2 4 1 5 1 2 2 4 3 2 5 3 1 3 4 4 5 1］

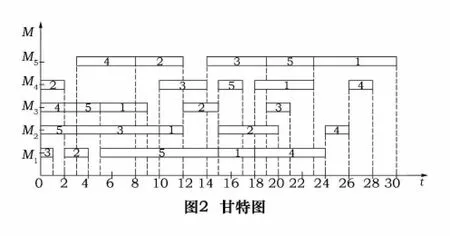
其對應甘特圖如圖2所示。

按照該染色體解碼后的參數，在車間實際加工以上5個工件僅需耗費30個單位時間。而該車間以往加工這批任務是憑借工人的經驗進行調度，一般需耗費37～40個單位時間。通過這個實例仿真可以看出，運用GA－SA－TS混合遺傳算法求解車間調度中的實際問題不但可行，還能減少加工用時。

在設定循環次數相等的情況下，對該例分別進行了混合遺傳算法和遺傳算法的仿真運算。如圖3b所示為該例在使用遺傳算法的過程中交叉和變異機制到達過的值。在相同初始條件的情況下，交叉機制中得到了最小值為31，但該結果在變異機制中產生了變化，使得相對最優值31丟失，并且在變異的過程中，搜索的范圍任停留在32～47之間，陷入局部最優，導致最終結果為32。

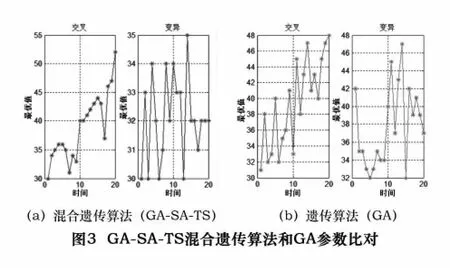
圖3a所示為該例在使用GA－SA－TS混合遺傳算法運算過程中模擬退火－交叉機制和禁忌搜索－變異機制分別到達過的值。可以看出，在初始條件相同的情況下，混合遺傳算法在交叉機制中得到的最優值為30;并且將其傳遞到了變異機制中進行操作，使得變異機制在操作的過程中搜索范圍由交叉機制中的30～55縮小到30～35，且在搜索的過程中多次到達了最優值30，并輸出。出現這樣的情況是由于模擬退火－交叉機制在操作的過程中通過Metropolis準則將交叉所得的最優值記錄下來，避免了最優值的遺失，并將最優值傳遞給變異機制進行操作。而禁忌搜索－變異機制通過基本變異方法，產生了一個以原有染色體為基礎的鄰域，從而提升了尋得最優解的可能性，擴大了搜索范圍。同時，每一條變異所得的染色體都進行特赦準則的判定，最終在所有變異的染色體中得到一條相對最優的染色體，而不是單純的進行變異操作。這樣的變異機制不但提高了遺傳算法的搜索能力，而且對每條變異的染色體和原始染色體都進行了優勝劣汰的操作，縮小了搜索范圍，因此避免了優秀個體在變異機制中的遺失。

4 結語

基于對遺傳算法易早熟和搜索能力差等缺點的考慮，本文提出了一種以遺傳算法為主體，融模擬退火算法和禁忌搜索算法思想于其中的混合遺傳算法(GASA－TS)。即在遺傳算法的交叉機制中融入模擬退火算法的思想，形成模擬退火－交叉機制。在遺傳算法的變異機制中融入禁忌搜索算法的思想，形成禁忌搜索－變異機制。通過將SA、TS融入到GA的操作中，使得遺傳算法的交叉和變異機制中都對染色體進行了優勝劣汰的操作，而不是待交叉和變異操作全部完成后再對染色體進行優劣評定，從而避免了優秀個體在交叉和變異操作過程中的遺失。并且通過對車間調度生產的實際算例仿真對以上論點進行了論證，通過仿真的結果可以看出，運用這種混合遺傳算法，對于解決車間調度系統的問題是可行的，并且較單純的使用GA算法而言，在解的質量方面有所提高。

［1］陶思南，傅鸝，蔡斌.一種求解車間作業調度的自適應混合遺傳算法［J］.計算機系統應用，2010，4(19):53 －57.

［2］何燕.基于遺傳算法的車間調度優化及其仿真［D］.武漢:武漢理工大學，2006.

［3］邢文訓，謝金星.現代優化計算方法［M］.北京:清華大學出版社，2007.

［4］GLOVER F.Future paths for integer programming and links to artificial intelligence［J］.Computers and Operations Research，1986(13):533－549.

［5］GLOVER F.Tabu search:partⅠ［J］.ORSA Journal on Computing，1989(1):190－206.

［6］METROPOLIS N，ROSENBLUTH A，ROSENBLUTH M，et al.Equation of state calculations by fast computing machines［J］.Journal of Chemical Physics，1953(21):1087 －1092.

［7］雷英杰，張善文，李續武，等.MATLAB遺傳算法工具箱及應用［M］.西安:西安電子科技大學出版社，2009.

［8］董宗然，周慧.禁忌搜索算法評述［J］.軟件工程師，2010(3):96－98.