關于R-C-K模型中加入第三部門的探討

涂 涵

（北京大學 光華管理學院，北京 100871）

0 引言

為了全面考慮經濟增長過程，必須考慮消費路徑，同時放開儲蓄率外生給定的假設，允許家庭能夠自我決策。Ramsey-Cass-Koopmans增長模型（簡稱R-C-K模型）和Diamond世代重疊模型（Overlapping-Generations Model，簡稱OLG模型）就是如此。與Solow模型一樣，這兩個模型同樣假設外生給定的勞動力和知識的增長率，只是放開了儲蓄率外生給定的假設，改由微觀經濟體——公司，通過在競爭市場中最大化利潤——和家庭，通過最大化一生效用來決定消費和儲蓄，從而推導出資本積累方程和經濟總量的動態變化。

新經典增長理論的基本模型R-C-K模型和OLG模型，都只考慮了兩部門情形：企業和家庭。但是現代經濟體除了分配有限資源給投資和私人消費之外，還會分配給公共部門。美國2008年的財政支出達到了4.72萬億美元，占GDP的33.1%，比1972年的3555億美元（占GDP1.24萬億美元的28.71%）增長了1228%！平均年增長率高達34.11%，而且在36年內一直持續快速穩定地增長。可見現實生活中，政府部門作為第三方，在生產、生活等經濟活動中占有非常重要的地位。

本文將加入政府部門，考慮三部門情形，探討政府支出和稅收對R-C-K模型造成的影響。

1 R-C-K基本模型

考慮一個有大量相同企業和H個相同家庭的經濟。每個企業擁有相同的生產技術Y=F(K,AL)，滿足一次齊次、單調遞增、Inada條件等假設。技術A和人口L的增長率外生，分別為。折舊δ=0。家庭的最優化問題為最大化一生效用：

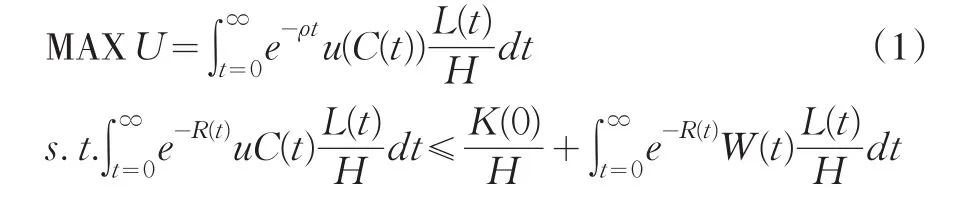
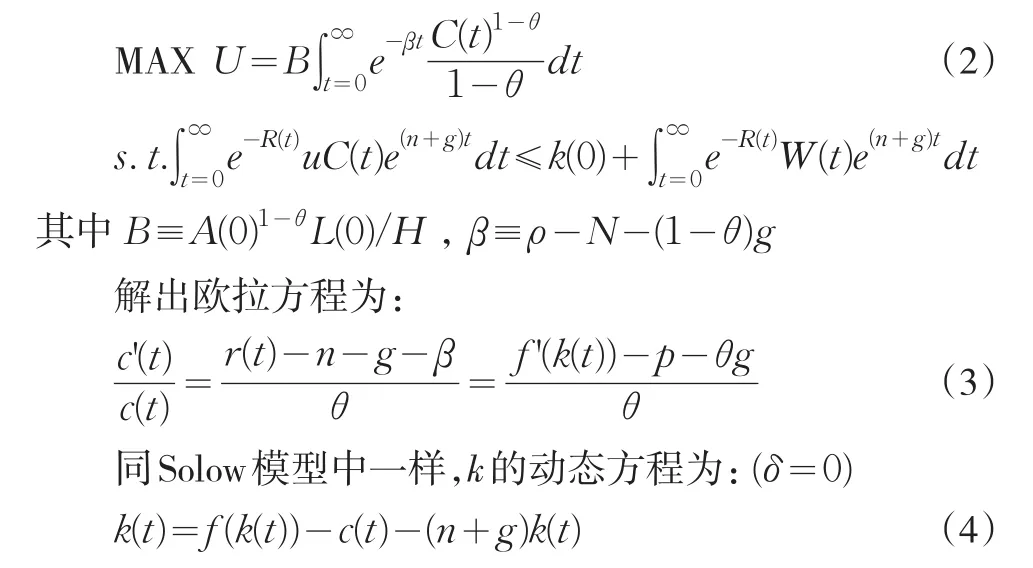
2 加入政府支出

假設政府每單位時間內每單位有效勞動購買G(t)單位產出，并對家庭征收一次性稅收。政府收支平衡。

（1）假設政府支出不影響家庭的效用函數和未來產出（即不用于投資），也不改變任何激勵。

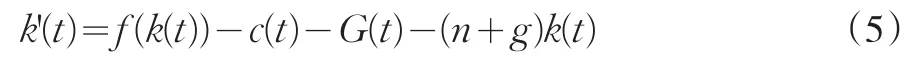
對應每一個k，由于政府支出G(t)，家庭消費相應減少G(t)，所以k'(t)=0的圖形向下移動。

因為c的動態方程不變，c'(t)=0不移動，由f'(k*)=ρ+θg可知k*不變。由于k'(t)=0向下移動，而k不發生突變，所以c會有一個不連續的跳躍。如果c不跳到新的鞍點路徑上，經濟將向左上方（c上升，k下降）或右下方（c下降，k上升）移動，都不滿足最優化。所以c從原鞍點路徑直接跳到新鞍點路徑，c減小的幅度等于G增長的幅度。由于k*不變，實際利率r*=f'(k*)不變。

在這種情況中，G完全擠出了c，k不變，說明政府支出沒有擠出投資，這是由家庭的跨期最優化選擇導致。

（2）假設政府支出G(t)不完全是公共消費，而是分為公共消費和公共投資兩部分，其中公共消費所占比例為m(0≤m≤1)，公共投資占比1-m。

由于有1-m的政府支出投入到資本積累中，所以k的動態方程變為：

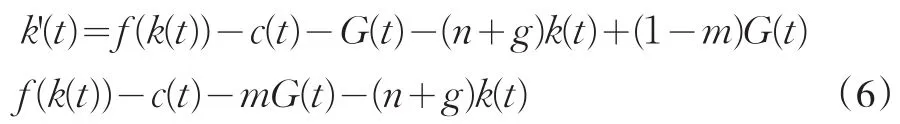
資本積累方程中的漏出項由（1）中的G(t)減小為mG(t)，所以k'(t)=0的圖形同樣向下移動，但是幅度沒有（1）大，所以c1*＜c2*＜c*，k*不變，從而實際利率 r*=f'(k*)不變。G部分擠出了c。

（3）上面假設政府支出不改變效用函數，現在假設政府支出與私人消費完全替代，即效用函數變為：

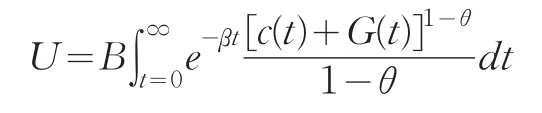
此時的最優化問題變為：

由于c(t)與G(t)完全替代，假設c(t)+G(t)=x(t)，x(t)代表總消費。變形后的最優化問題：

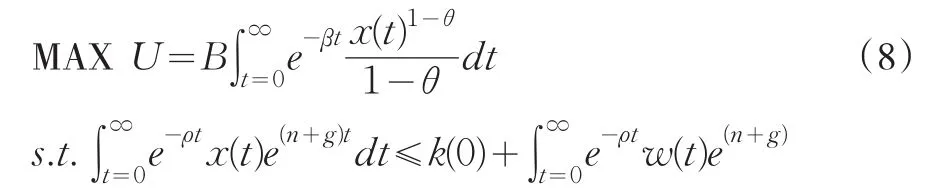
得到一階條件為：

資本積累方程仍為（2.5）：

假設政府有一個短暫的支出變化，t0時宣布從GL提高到GH，在t1時重新降低到GL。則在t0前和t1后使k'(t)=0的函數為c(t)=f(k(t))-GL-(n+g)k(t)，t0到t1之間為c(t)=f(k(t))-GH-(n+g)k(t)，即向下平移GH-GL。使c'(t)=0的方程仍為 f'(k(t))=ρ+θg，從而k*不變。

在這個假設下，即使政府支出重新降低到GL是可以預期的，c在t1時仍然會有一個跳躍，這與基本假設的結論不同。因為此時假設消費c和政府支出G在效用函數中是完全互補關系，如果在t1時c不發生跳躍，邊際效用則會有一個不連續的跳躍，與最優化矛盾。所以在t0政府支出提高到GH時，c下降GH-GL，跳躍到新的鞍點路徑上，而在t1降低到GL時，c上升GH-GL，跳回到原來的鞍點路徑上。c+G保持不變。

預期的支出變化（anticipated change）和沒有預期到的支出變化（unanticipated change）對經濟的影響相同，當G變化時c同時發生方向相反、幅度相同的變化，跳躍到新的鞍點路徑。如果政府永久地提高支出，即t1趨于正無窮，那么c將會永久下降GH-GL，跳躍到新的鞍點路徑上。所以預期和沒有預期、暫時性和永久性的財政變化，對c和k的影響是一樣的。

3 資本稅收

3.1 稅率為τ的資本稅

假設政府宣布要對資本收入收取稅率為τ的資本稅，從而實際利率變為r(t)=(1-τ)f–(k(t))。歐拉方程變為

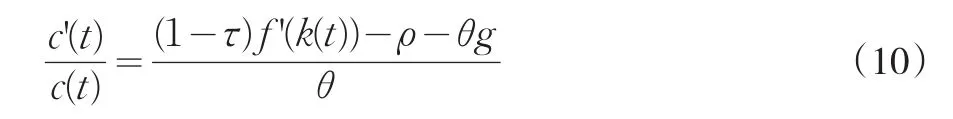
從而使c'(t)=0的方程變為：

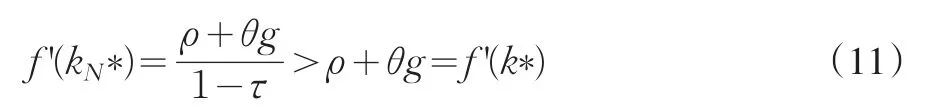
由f’是減函數可知kN*＜k*，c'(t)=0的圖像向左移動。

3.1.1 政府把所收稅款以一次性轉移支付的形式返還給家庭

在這個假設下，k的積累方程為：

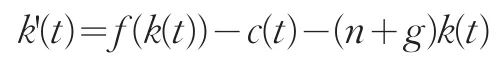
與沒有稅收時的情況（3.1.4）相同，圖像不發生移動。

k*由以往投資所決定，不能不連續地跳躍改變。如果在收稅時c不發生跳躍，則經濟處于新的鞍點路徑下方，經濟會向右下方（c下降，k上升）移動，資本將過度積累。如果c向下跳躍，則更加遠離新的鞍點路徑，從而發散。所以c只能向上跳躍。在宣布收稅的同時，使得c'(t)=0的圖像向左移動，生成新的鞍點路徑，c從E向上跳躍直接到達新鞍點路徑上的A點，然后c和k沿新鞍點路徑移動到新平衡增長路徑EN。kN*＜k*，cN*＜c*，這是由于對資本收入收稅，投資對家庭的吸引力（實際利率）下降，導致儲蓄下降、消費上升。但隨著投資的減少，資本積累減少，從而產出減少，導致消費和儲蓄都減少，整個經濟會下降到一個更低迷的狀態，即從E變到EN。

接下來假設有很多處于平衡增長路徑的同質的經濟體，家庭偏好相同（參數ρ、θ相同），但是每個國家的資本稅率τ有所不同。τ越高，資本收益對家庭的吸引力即實際利率越低，從而家庭的儲蓄動機也會越低，儲蓄越少，從而平衡增長路徑上的儲蓄率關于稅率遞減（具體證明略）。

那么生活在低稅率τ、高儲蓄、高k*國家中的人們有沒有向低儲蓄的國家投資的動機呢？因為工人們的偏好等相同，參數ρ、θ、g相同，所以稅后資本回報率(1-τ)f'(k)=ρ+θg在不同國家之間是相同的，從而人們沒有動機向國外投資。

3.1.2 如果政府不把所收資本稅款以轉移支付的方式返還給家庭

如果政府不進行轉移支付，歐拉方程仍如（1）中（10）式一樣：

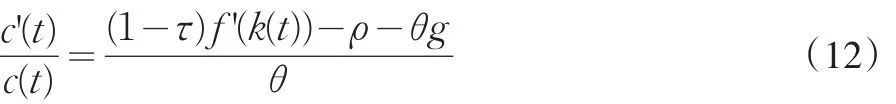
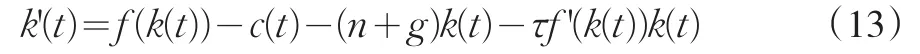
而資本積累方程因為漏出項增加了資本稅收而變成：最后一項就是資本稅收，在（1）中因為政府以轉移支付返還給家庭，該項被抵銷從而方程不變。所以資本稅收漏出使得k'(t)=0的圖像向下移動了τf'(k(t))k(t)的幅度。

同樣k*由歷史投資積累決定，不能不連續地跳躍改變。由于最優化，c*可能會不連續地跳躍到新鞍點路徑上或者不跳躍，這就必須討論c*與新鞍點路徑的相對位置關系。如果c*處于新的鞍點路徑上，則無須跳躍，經濟將沿新的鞍點路徑移動到新的平衡增長路徑上去；如果c*不在新的鞍點路徑上，那么c*會立刻跳躍到新鞍點路徑上，再沿著新的鞍點路徑移動到新的平衡增長路徑上去。同（1）一樣，新的平衡增長路徑的k*和c*都比不收稅時的k*和c*小。

3.1.3 預期的稅收變化和轉移支付

(1)永久的稅收

假設在t0時政府宣布從t1開始對資本收入收取稅率為τ的資本稅。從而實際利率變為r(t)=(1-τ)f–(k(t))，在t1之前，c和k的動態方程為：

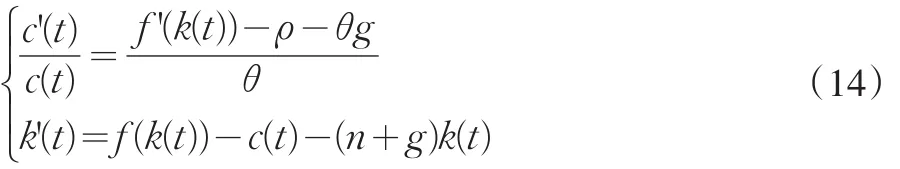
在t1之后，收稅使得c和k的動態方程變為：

在t1開始收稅之后，c'(t)=0的圖像向左平移，k'(t)=0的圖像不動。

因為t1時的稅收變化已經確定，c不會有不連續的跳躍，否則與最優化矛盾。在t0宣布政策時，c*會有一個跳躍，使得在t1時c是連續變化的。若c向下跳躍，則在t1之前，經濟會向右下方（c減小，k增大）移動，資本過度積累；若c向上跳躍到D點或D點以上，在t1之前會繼續向左上方（c增大，k減小）移動，t1時一定會處于新鞍點路徑之上，t1時一定會有跳躍，與最優化矛盾。所以c向上跳躍到D點與E點之間的某一點A；在t0到t1之間，動態方程仍是原來方程，所以c在t1之前會繼續向左上方（c增大，k減小）移動，到t1時正好到達新鞍點路徑上的B點，此時新的c'(t)=0的圖像開始作用，經濟沿新鞍點路徑移動到EN。

(2)暫時的稅收

假設在t0時政府宣布從t1到t2對資本收入收取稅率為τ的資本稅，在t1前和t2后不收稅。所以原始的動態方程為：

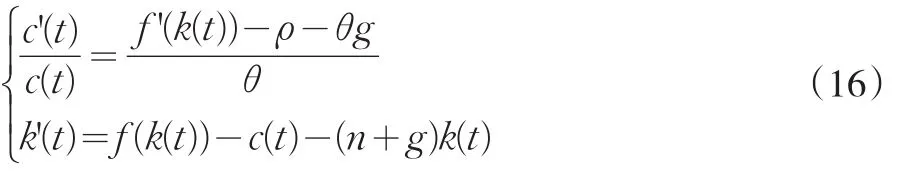
在收稅t1到t2期間，變為：

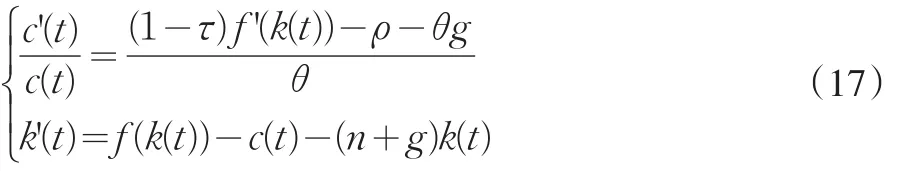
從而在t1前和t2后，c'(t)=0的方程為 f'(k*)=ρ+θg；在t1到t2期間，c'(t)=0的方程為 f'(k*)=(ρ+θg)(1-τ)，向左平移。

由于該政策的稅收變化可以預期，在t1和t2兩個時點處c和k不會有不連續的跳躍，從而得知t2時經濟處于原鞍點路徑上。通過分類討論可知在t0時c會向上跳躍到A，此時c'(t)=0,k'(t)＜0，k下降，經濟向左上方（c增加，k減小）移動，在t1時到達B點。若B在新的鞍點路徑或上方，則在t2時必須有不連續的跳躍才能回到原鞍點路徑上，所以B一定在新的鞍點路徑下方。t1到t2期間由新的c'(t)=0,k'(t)＜0的方程即 f'(k*)=(ρ+θg)(1-τ) 決定動態變化，c和k都下降，向左下方移動。

若向左下方移動時穿過了新的c'(t)=0，那么經濟會向左下方移動直至最后崩潰。所以經濟不會穿過新的c'(t)=0。穿過k'(t)=0之后，在新的動態方程作用下c下降，k上升，向右下方移動，從而在t2時恰好到達原鞍點路徑上的點C。t2之后沿著原來的鞍點路徑移動到原來的平衡增長路徑E處。

3.1.4 未預期到的稅收變化和轉移支付

(1)永久的稅收

假設在t0時政府突然宣布開始對資本收入收取稅率為τ的資本稅。在t0前，c和k的動態方程與（16）相同，為：

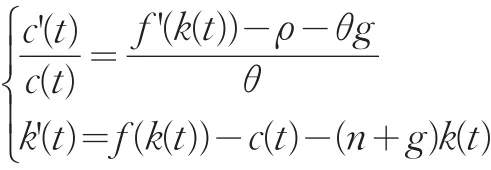
在t0之后，由于開始收稅使得c和k的動態方程變為：

在t0開始收稅之后，c'(t)=0的圖像向左平移，k'(t)=0的圖像不動。

由于這個變化是沒有預期到的，c在t0發生不連續的跳躍并不與最優化矛盾。這種情況與（3.1.1）相同，由（3.1.1）可知，k在t0不變，c會向上跳躍到新鞍點路徑上，然后沿著鞍點路徑移動到新平衡增長路徑EN上。

(2)暫時的稅收

假設在t0時政府突然宣布從t0到t1對資本收入收取稅率為τ的資本稅，在t1之后不收稅。所以原始的動態方程為：

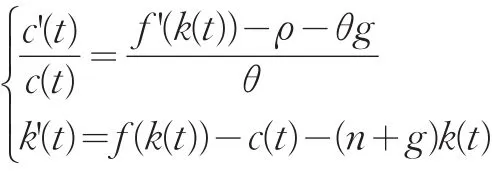
在收稅t0到t1期間，變為：

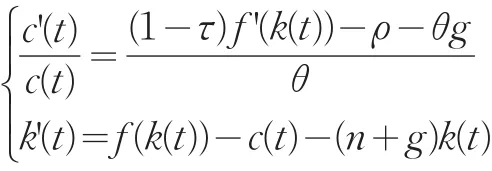
從而在t0之前和t1之后，c'(t)=0的方程為 f'(k*)=ρ+θg；在t0到t1期間，c'(t)=0的方程為 f'(k*)=(ρ+θg)(1-τ)，向左平移。

由于在t0時能夠預期到t1的情況，不會有突變。通過分類討論知道在t0時c向上跳躍：如果跳到新鞍點路徑與c'(t)=0交叉的M點處，那么會沿著新鞍點路徑移動，在t1只有不連續的跳躍才能回到原鞍點路徑上，與最優化和預期矛盾；如果跳到M點以上，那經濟會一直在新的鞍點路徑以上，在t1時同樣必須有一個不連續的跳回到原鞍點路徑上的跳躍。所以c向上跳躍到E與M之間的某點A處。然后在新的動態方程的作用下，向左下方（c和k都下降）移動，移動路徑一直處于新的鞍點路徑之下。從上向下穿過k'(t)=0后，k增加從而向右下方移動。t1時恰好到達原鞍點路徑B，然后沿原鞍點路徑移動到原平衡增長路徑E上。

3.2 一次性稅收T

假設政府宣布收取一次性稅收T

（1）若政府以轉移支付返還給家庭，則動態方程均不發生變化，經濟在平衡增長路徑不移動。

（2）若政府以公共消費的方式使用了稅收，動態方程變為：

此時k'(t)=0向下平移T，而c'(t)=0不動，故c向下跳躍到新平衡增長路徑上。

4 消費稅τc

如果政府對家庭征收稅率為τc的消費稅，那么家庭的最優化問題變為：

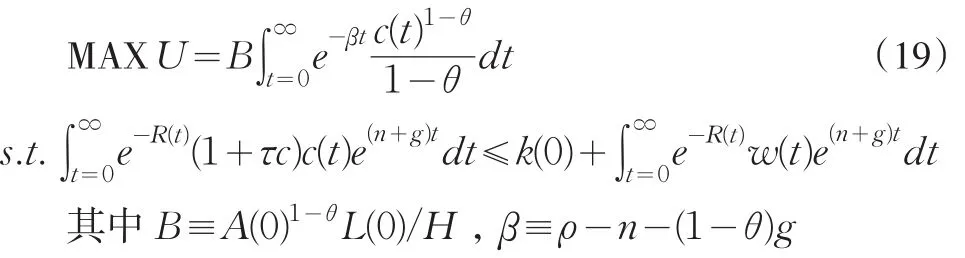
解出歐拉方程為：

與不征稅的情況一致。

由于消費從c(t)增大到(1+τc)c(t)，經濟中的漏出項增大，從而k的動態方程為：

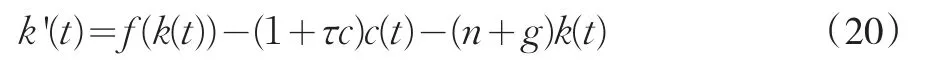
使得k'(t)=0的函數為：

比原圖像向下平移。與有政府支出的R-C-K模型的相位圖擁有相似的動態變化。

5 結論與未來擴展

政府支出和稅收作為經濟中的漏出項，對c和k有一定的負面作用。但是瞬間的改變和之后的動態變化會因為政府支出和稅收的可預見性及是否轉移支付等而有所不同，具體情況需要具體分析。總而言之，隨著政府支出和稅收的增加，c和k呈下降趨勢。

本文只考慮了一次性稅收、資本稅和消費稅，其他如個人所得稅、公司稅、財產和遺產稅等等很多稅收對經濟中各個變量的動態變化和平衡增長路徑都會有相應的影響和扭曲。其次，本文討論政府支出改變效用函數的情況，而沒有討論生產函數變化的情況。同效用函數一樣，政府支出、各種稅收也會對生產函數產生影響，從而對經濟變量產生影響和扭曲。再次，投資的調整成本，或者把資本分為實物資本和人力資本分別加以討論，也會推導出不同結果。技術增長外生的不合理假設還能進行修正和改善，20世紀 80年代中期以來,以Romer（1986）、Lucus(1988)等為代表的新增長理論就是進一步將技術進步內生化，將技術外生增長的設定改為帶有內生增長率的人力資本變量進行分析。還可以考慮家庭偏好、各種增長率等參數變化，效用函數和生產函數形式的變化，以及市場不完全、信息不完全、壟斷等情況。

可以繼續推廣到四部門情形，即考慮開放市場，討論要素流動性，各國技術及增長率、人口及增長率、家庭偏好等重要參數的差異，和貿易摩擦、貿易壁壘、關稅等問題。

可以探討的內容有無限可能性，一一分析是不現實的，而且模型會變得龐大和繁雜。最全面刻畫現實經濟的模型只有一個，就是現實自身，我們研究的理論模型都會有一些對真實經濟簡化的假設。只要得出的結論對現實有一定的解釋力和指導性，我們所做的假設就是合理的。

[1]Barro，Robert J.,Sala-i-Martin，Xavier.Economic Growth[M].US：MIT Press，2003.

[2]Romer，David.Advanced Macroeconomics(3rdEdition)[M].US：Mc?Graw-Hill，2006.

[3]Mankiw，N.Gregory，Romer，David，Weil，David N.A Contribution to the Empirics of Economic Growth[J].The Quarterly Journal of Econom?ics，1992,107.

[4]謝拉·C·道.經濟學方法論[M].上海：上海財經大學出版社，2005.

[5]美國財政支出[EB/OL].http://www.heybrain.com/notheal/article/2909.

[6]鄒薇.宏觀經濟學[M].北京：中國社會科學出版社，2000.