范德蒙陣列糾刪碼在嵌入式系統中的應用
程志洪,龔志勇
(中國電子科技集團公司第五十四研究所,河北石家莊 050081)
0 引言
范德蒙陣列糾刪碼是一種低密度糾刪碼,具有較低的迭代譯碼復雜度,而且是目前接近信道容量限的最佳編碼技術之一。
衛星數字化視頻廣播系統(DVB-S)采用卷積碼與里德-所羅門編碼(Reed-Solomon Codes,RS)級聯糾錯。衛星數字化視頻廣播的第2代標準(DVBS2)系統采用低密度校驗碼(LDPC)與BCH碼級聯糾錯。空間數據系統咨詢委員會(CCSDS)推薦采用卷積碼與RS碼級聯或Turbo碼等糾錯。在網絡數據傳輸、數據存儲等通信系統中,多采用糾刪碼來提高數據傳輸可靠性。在Internet工程任務組織(IETF)草案中,推薦采用RS糾刪碼、LDPC糾刪碼和數字噴泉碼等來提高網絡通信的可靠性和有效性。分布式存儲系統和磁盤陣列技術(RAID)中也采用了糾刪碼來提高數據的可靠性[1]。
1 糾刪碼編譯碼
糾刪碼具有在嵌入式系統和計算機上處理速度快的特點。嵌入式系統輸出的數據經過無線通信系統傳輸,當系統可靠性不能達到指標要求時,可以考慮在嵌入式系統中加入糾刪碼來提高無線通信系統的可靠性[2]。
目前,有關糾刪碼的研究主要集中在兩大類,一類是低密度糾刪碼,如LDPC糾刪碼、數字噴泉碼等,一類是傳統的編碼方法如RS類糾刪碼。LDPC糾刪碼依靠單一異或操作產生冗余,具有相對較低的計算復雜度。盡管數字噴泉碼的研究已取得一些可喜成果,但目前的應用還不是非常廣泛。RS糾刪碼為最大距離可分(MDS)碼,具有最好的糾刪性能[3],它平衡了容錯性能和碼利用率,但是它在糾刪碼中具有較大的計算復雜度[4]。
一個(n,k)糾刪碼是把k包數據編碼為n包數據,使得用這n包數據中的任意k包數據均可重構原來k包源數據,其中每包數據長度為m(m為正整數)個字節,其編譯碼過程示意圖如圖1所示。糾刪碼通常適用于數據整包丟失或包中有數據錯誤的通信系統中。
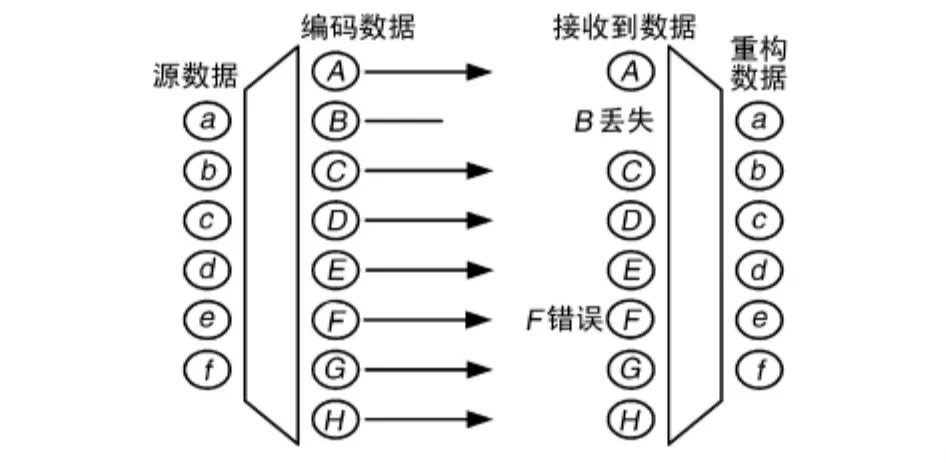
圖1 糾刪碼編譯碼過程
原始數據包為a包~f包,編碼后數據包為A包~H包,其中G包和H包為冗余包,輸出編碼數據 G 的生成過程可示意為 G=f(a,b,c,d,e,f),f為滿足一定規則的異或運算。對RS糾刪碼來說,f為一個生成矩陣,生成矩陣可以為范德蒙矩陣和柯西矩陣,對應的糾刪碼分別成為范德蒙糾刪碼和柯西糾刪碼。對LDPC糾刪碼來說,F為一個與二部圖對應的稀疏矩陣。糾刪碼的譯碼過程為G=f'(a,b,c,d,e,f),其中 f'為 f的逆運算。
2 范德蒙陣列糾刪碼算法
若選取糾刪碼的生成矩陣為范德蒙矩陣或柯西矩陣,則可得相應的糾刪碼——范德蒙碼(Vandermonde Code,VC)或柯西碼(Cauchy Code,CC),它們都屬于RS碼類。
2.1 范德蒙矩陣
設a為佳伽羅華域上的8次本原多項式p(x)=1+x2+x3+x4+x8,則伽羅華域GF(28)可由p(x)的本原根 a 來生成:GF(28)={0,1,a,a2,…,a254},其各個元素互不相同。構造如式(1)所示的n×k范德蒙矩陣G,其中n>k。

2.2 范德蒙碼編碼算法
使用上面的生成矩陣G進行編碼,y=Gx,其中x=(x0,x1,…,xk-1)T,y=(y0,y1,…,yn-1)T,可以看出編碼后的數據y完全和源數據不同,不是系統碼,這種編碼一定程度上增加了信息的保密性,但是也大大增加了編碼和解碼的復雜度,并不適用。線性碼的生成矩陣G的構造常常使用k×k單位矩陣與(n-k)×k的范德蒙矩陣聯合構成。使用Gauss-Jordan消去法,把G轉換為式(2)所示的形式:

式中,Ik為k級單位矩陣。在矩陣變換過程中,所有的運算都是伽羅華域上的模2運算。
待編碼的k包數據為D:

式中,m為任意正整數,包長可以為任意字節數。編碼可表示為(假設需要L(L≤n-k)個檢驗包):
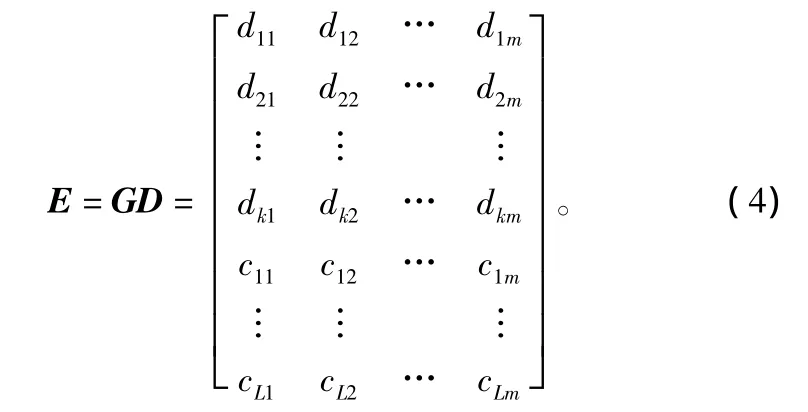
矩陣E的前k包為待編碼數據D,直接復制原始數據,只需計算L個檢驗行。例如 c11=a11*d11+a12*d21+… +a1k*dK1,“+”和“* ”為伽羅華域上的運算。
2.3 范德蒙碼譯碼算法
假設接收到的數據第2行與第k行發生錯誤(1行中錯誤比特數≥1,整行標識為錯誤),則從冗余行中選則2行構造如式(5)所表示的矩陣:

并對G'求逆,其逆矩陣為G'-1,則恢復數據可用式(7)表示:
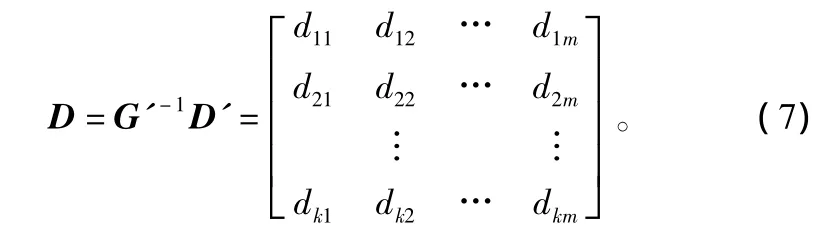
只需計算D的第2行和第k行,其他行直接從D'中復制即可。
2.4 范德蒙碼編譯碼快速算法
在范德蒙碼編譯碼過程中,所有涉及到矩陣變換過程的運算都是伽羅華域上的模2運算。伽羅華域上的運算與實數域上的運算不同,其主要區別為[5]:
①伽羅華域上的加減運算以域元素的矢量形式進行,加減運算為域元素的矢量表示所對應位模2加;②域上元素見的乘除運算以本原元素的形式進行,乘除運算為本原元素的冥次模加減。
由式(5)和式(6)可知,編解碼過程中涉及大量伽羅華域乘法與加法運算。為了提高速度,事先把所有的可能加法和乘法運算結果都計算出來存儲在表中,實際運算的過程中只需進行查表,可大大提高處理速度。
3 仿真結果分析
3.1 信道誤碼仿真
圖2為DVB-S傳輸系統的結構框圖。在Matlab中構建該系統,糾錯碼外碼采用RS碼,內碼采用卷積碼。RS選用(255,239),交織采用32×8卷積交織,卷積編碼采用(2,1,7),調制方式采用BPSK,AWGN信道的SNR值設為1.14 dB[6]。經過Viterbi譯碼、解交織和RS解碼之后誤碼率為1.0×10-5。

圖2 信道誤碼仿真框圖
通過對該系統的仿真,得到其誤碼出現分布如圖3所示,其中橫軸為統計數據包的序號,縱軸為數據包內誤碼個數。可以看出,數據經過圖2所示通信系統處理后,誤碼不再體現AWGN信道的隨機誤碼特性,誤碼的表現形式為一包數據中出現多個錯誤,且出現誤碼的時間間隔較大。該仿真結果表明DVB-S適合采用糾刪碼來進一步降低系統的誤碼率。
3.2 糾錯性能仿真
為了驗證糾刪碼與無線通信系統中的糾錯碼級聯使用的效果及測試糾刪碼的運算速度,設計了如圖4所示的仿真系統。在數字信號處理器(DSP)上對數據進行糾刪碼編碼,編碼之后的數據DVB-S系統傳輸,并把最終的數據送進計算機由計算機完成糾刪碼解碼工作。
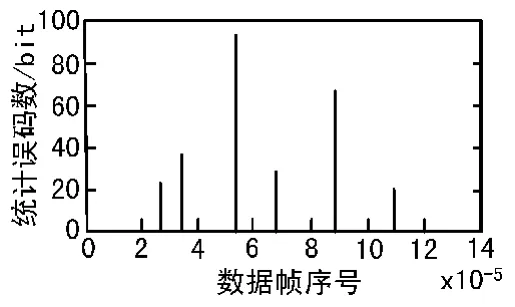
圖3 誤碼出現分布圖
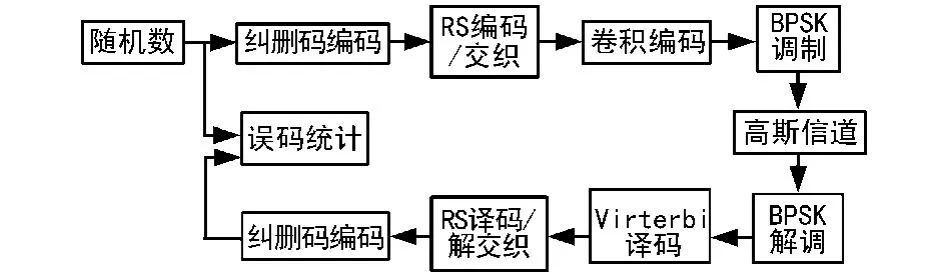
圖4 仿真系統結構框圖
DSP 選用 TI TMS320C6416,頻率為850 MHz,片內RAM為1 MB,計算機配置為 CPU P4,主頻為3.0 GHz,4 G 內存。
在該驗證系統中RS糾刪碼參數如下:源數據包k=17,包長N=256字節,編碼之后數據包n=20,即冗余包為3包。經過實際測試:當圖2所示的系統誤碼率為1.0×10-5時,加入糾刪碼之后的誤碼率將為1.0×10-8左右,當圖2所示的系統誤碼率為1.0×10-6時,加入糾刪碼之后的誤碼率將為1.0×10-10左右。隨著信道誤碼率的提高,糾錯性能會下降,如果增加冗余包,能夠進一步提高糾錯性能。
DSP數據輸出速率為8 Mbps時,占用的DSP處理時間非常少,計算機進行糾刪碼解碼運算占用的CPU為2%左右。
4 結束語
通過分析范德蒙陣列糾刪碼的編解碼算法,得到一種范德蒙碼編解碼快速算法。將范德蒙碼編解碼快速算法應用于Matlab構建的系統信道誤碼仿真。實驗結果表明,范德蒙陣列糾刪碼與通信系統中的糾錯碼級聯使用大大提高系統的抗誤碼性能,在利用快速算法完成較高數據速率的實時處理,進一步提高了系統的可靠性。
[1]LIN Shu,COSTELLO D J.著差錯控制編碼[M].晏堅,何元智,潘亞漢譯.北京:機械工業出版社,2007.
[2]RIZZO L.Effective Erasure Codes for Reliable Computer Communication Protocols [J]. ACM Computer Communication,Review,1997,27(2):24-36.
[3]張傳達,李小文.卷積編碼及其 Viterbi譯碼的實現[J]. 無線電工程,2006,36(7):45-48.
[4]王新梅,肖國鎮.糾錯碼-原理與方法[M].西安:西安電子科技大學出版社,2002.
[5]向茜,劉釗.伽羅華域上代數運算的最簡實現[J].電子科技大學學報,2000,29(1):5-8.
[6]李雋.衛星導航信號模擬器體系結構分析[J].無線電工程,2006,36(8):30-21,39.

