上海質子治療裝置慢引出RFKO研究

史 丹 歐陽聯華 谷 鳴

(中國科學院上海應用物理研究所 上海 201800)

質子束治療癌癥優于常規射線治療(電子、X射線、γ射線)。治療控制要求加速器提供均勻、穩定且快速開關的束流，其占空比須可調。因此，采用同步環慢引出的方式。醫用質子加速器慢引出設計中，將質子從環內引出有兩類方法。

第一類方法是將相空間穩定區三角形面積壓縮，使穩定區外圍粒子進入共振。相空間三角形面積與規一化六極磁鐵強度的平方成反比，與粒子的tune值與三階共振頻率的距離平方成正比。減小相空間三角形面積可增大六極磁鐵強度；或調節四極磁鐵強度使粒子的tune值逼近三階共振線，此方法需改變環束流的光學參數[1]。

第二類方法是先調節束流參數(發射度，tune值等)至臨界值，維持不變，通過激勵使粒子進入共振。一是縱向激勵，如使用betatron core和縱向隨機電場(stochastic noise)加速(或減速)，提高粒子進入共振的速度，使不同動量的粒子同時進入共振。我們采用橫向 RF-knockout(RFKO)電場激勵，使粒子發射度增長，被“打”出穩定區(knockout)，進入共振。首先是穩定區外圍振幅大的粒子溢出穩定區，然后是穩定區中心區域的振幅較小的粒子也被激勵，溢出穩定區，直至所有粒子均被引出。

RFKO的優點是：(1) 引出時環的Lattice參數保持不變；(2) 粒子引出時進入septum的橫向位置(spiral step)保持不變；(3) 若與RF cavity縱向電場配合，粒子的關斷時間可達100 μs，宜于開展高精度的呼吸門控和點掃描治療。RFKO方法要求環色品很小(最好為 0)，則不同能散的粒子具有相同的tune值，不會通過同步振蕩進入共振。但是零色品的環易引起束流頭尾不穩定性[2]。

1 RFKO理論基礎

1.1 三階共振Hamiltonian函數

不考慮偏能粒子和閉軌畸變，粒子運動歸一化相空間的Hamiltonian方程[3]為

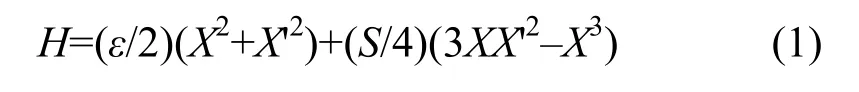
其中，ε= 6πδQ，δQ為粒子tune值離三階共振的距離，S為六極鐵強度，X、X'為坐標。由式(1)可得三階共振的穩定區和非穩定區及其邊界(separatrices)和穩定點以及穩定區面積，分析粒子在穩定區內、邊界上和穩定點附近的運動行為。

定義粒子的歸一化振幅和發射度分別為A=(X02+X0'2)1/2，E=πA2。引出時，調整四極磁鐵的強度以改變 tune值的距離δQ，同時調整六極磁鐵的強度S，相空間橢圓變成三角形。若粒子振幅小于穩定三角形面積Estable，該粒子是穩定的。

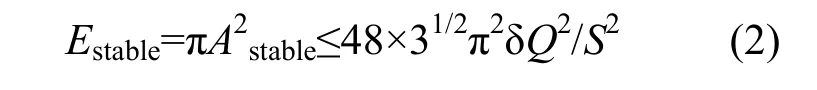
對于某一個特定振幅，δQ小于以下值時粒子將失去穩定：

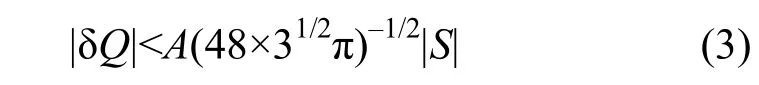
同樣，對某一個特定的δQ，粒子振幅大于以下值時，將失去穩定：

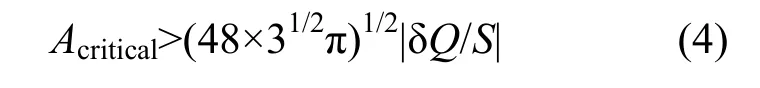
1.2 RFKO理論基礎

當環上存在RF kicker(這里簡化為橫向RF正弦振蕩)時，Hill方程[4]變為：

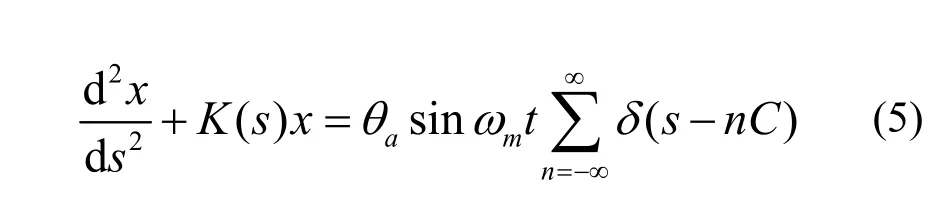
式中，K(s)為環聚焦強度，θa為橫向RF kicker強度，ωm為其頻率，t=s/(βc)，δ函數表示粒子每循環一圈被激勵一次。

對式(5)進行 Floquet變換，求解變換后方程的特解和通解, 并給定初始條件x=x'=0；當RF kicker頻率與粒子回旋頻率之比vm等于或接近 tune值v時，式(5)的解為：

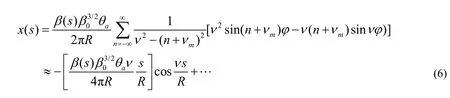
其中，R為環周長，β0為RF kicker所在處的β函數。

上海質子治療加速器環周長28.4 m，v=5/3，圖1為受RF knockout激勵粒子橫向位置隨時間變化結果，可見振幅為0的粒子，經RF kicker激勵，振幅呈振蕩性線性增長。

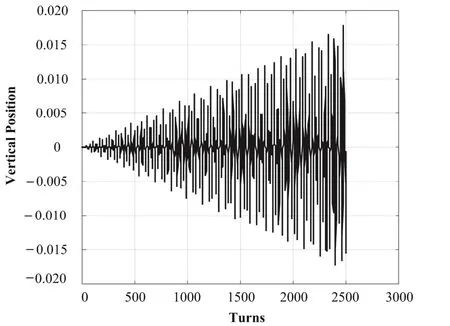
圖1 受RF knockout激勵，粒子橫向位置隨時間呈振蕩性線性增長Fig.1 The horizontal position of particles vs the time.The position oscillation grows linearly with the time,due to RF knockout motivating.

2 幅度調制(AM)

RFKO可增大引出粒子的振幅，擴大其發射度，使粒子溢出穩定區而被引出，但引出束流的幅度與RFKO的踢角并不呈線性關系。根據HIMAC資料[5]，對于隨機RFKO電場信號，1σ偏差可達±70%，調制后1σ偏差<±20%。因此，AM調制以達到預想的引出束流幅度結構及引出效率，是非常關鍵的。可使用簡化的一維模型獲得AM函數[6]，得到平滑束流。徑向分布函數在規范化的相空間可寫成瑞利分布，即

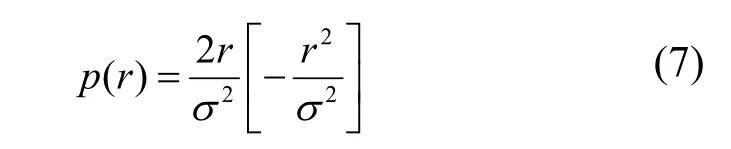
其中，σ2=2εrms，σ為瑞利分布的標準差，εrms為均方根發射度。

假設徑向幅度大于0r的會被引出，引出粒子數為extN，引出束流的時間結構為

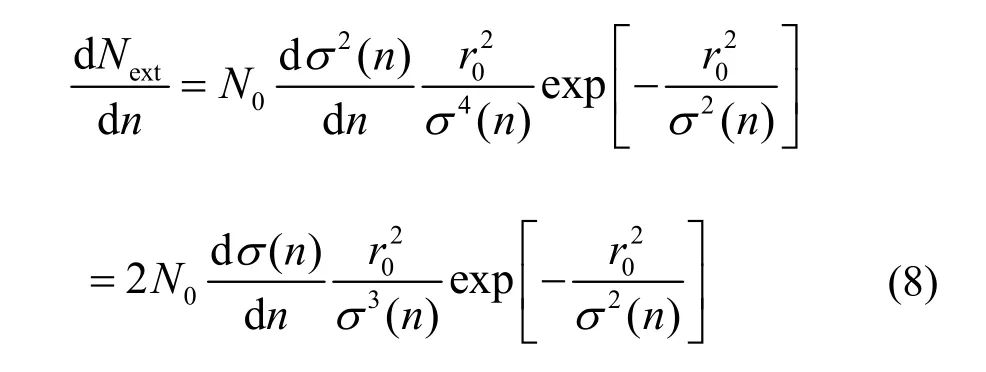
N0為引出前環內的粒子數。假定σ2與粒子轉的圈數成正比，kick角幅度θ依賴于時間，使用常數k指代與RFKO帶寬相關的系數，則σ值的增長為：

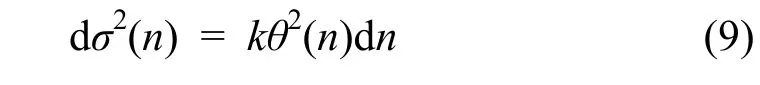
為獲得平滑的溢出且引出所有粒子，dNext/dn引出時保持不變，則平滑引出的AM函數為

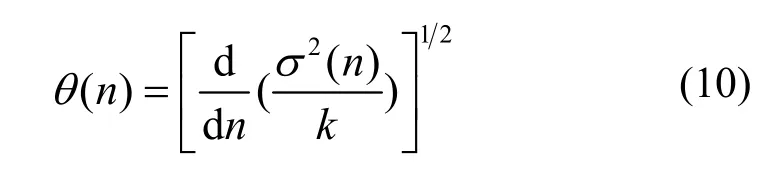
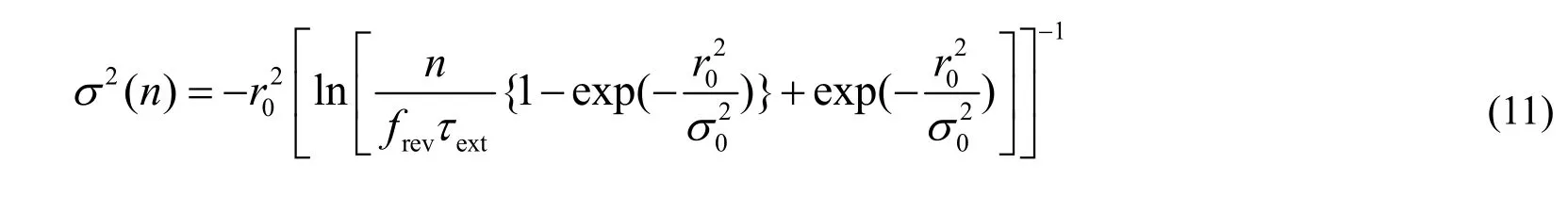
式中，σ0為σ(n)的初始值，τext為引出持續時間。估算k=312，r0=9.09×10?3，σ0=3.16×10?3，kick 角分別為0.5、1.0、2.0 μrad，引出時間結構的解析曲線如圖2。若每圈引出1000個粒子, 則θ和n的關系如圖3。

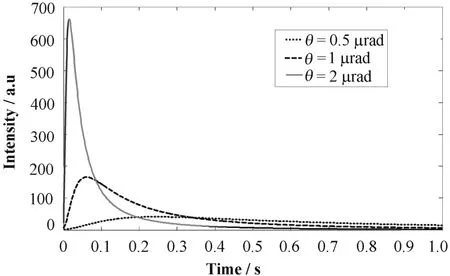
圖2 恒定kick角下的引出時間結構, Kick角分別為 0.5、1.0、2.0 μradFig.2 The extracted spill structure at kick angles of 0.5, 1.0 and 2.0 μrad.

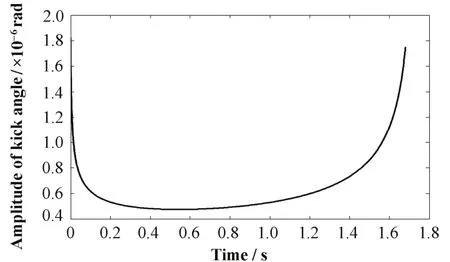
圖3 θ和n的關系曲線(每圈引出1000個粒子)Fig.3 The θ-n curve, with an extracted beam of 1000 protons.

3 數值模擬

3.1 引出粒子分布情況模擬

運用軟件 WinAGILE[7]研究粒子引出情況，設置動量偏差(dp/p)后，高斯粒子束散布在三角區內，引出初期，一部分不穩定粒子進入非穩定區，進而被引出，且引出粒子數服從指數分布；由于動量偏差，粒子束開始向靜電切割板即不穩定區域移動。加速若干圈后，粒子被引出，引出數目和圈數服從高斯分布(圖4a)。同樣設置動量偏差，1000個均勻分布粒子引出亦服從均勻分布(圖4b)。與高斯分布不同的是，分界線內的粒子在全部引出前，不穩定粒子未被引出。

3.2 Tune值與引出粒子關系

調整四極磁鐵強度即改變ΔQ，保持Δp/p=0，且S= –4.2259不變，得到臨界值 ΔQ=|Qp–Qr|=0.004202，Qr即tune值5/3，此時四極磁鐵強度QF為–2.109732。表1顯示，|ΔQ|<0.004202，有粒子被引出；相反，則無粒子被引出。ΔQ接近0時，粒子幾乎完全引出，|ΔQ|逐漸增大，粒子引出數相應減少。

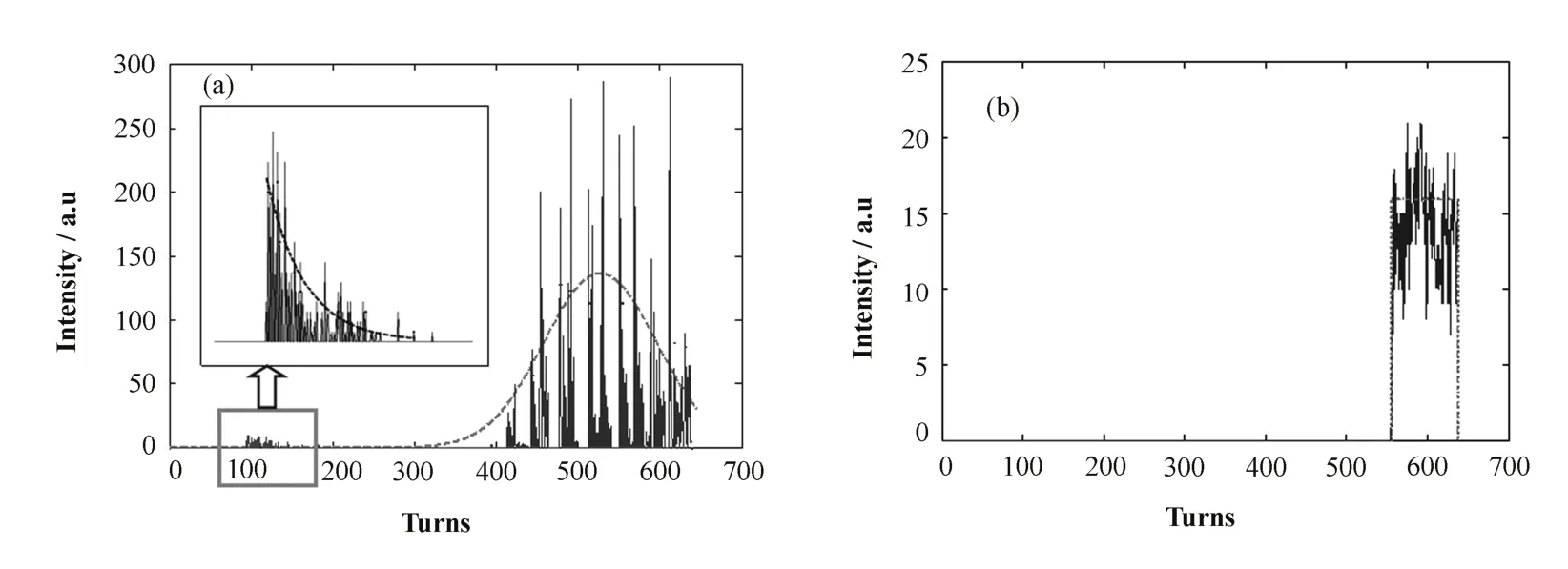
圖4 5000個高斯粒子(a)和1000個均勻分布粒子(b)的引出圖Fig.4 Extraction of 5000 Gaussian particles(a) and 1000 uniform distribution particles(b).

3.3 共振驅動六極磁鐵強度與引出關系

保持能散不變(Δp/p=0)，ΔQ =–0.003609 不變，模擬發現六極磁鐵強度S的臨界值為–3.5(表2)。對S值和剩余粒子數擬合，得到擬合函數式Nremain=373.6e0.01638S+1123e0.1549S(圖5)。|S| = –3.5, 粒子幾乎無引出，在六極磁鐵強度不斷減小，即|S|逐漸增加時，粒子慢慢被引出，模擬仿真驗證了相關理論。

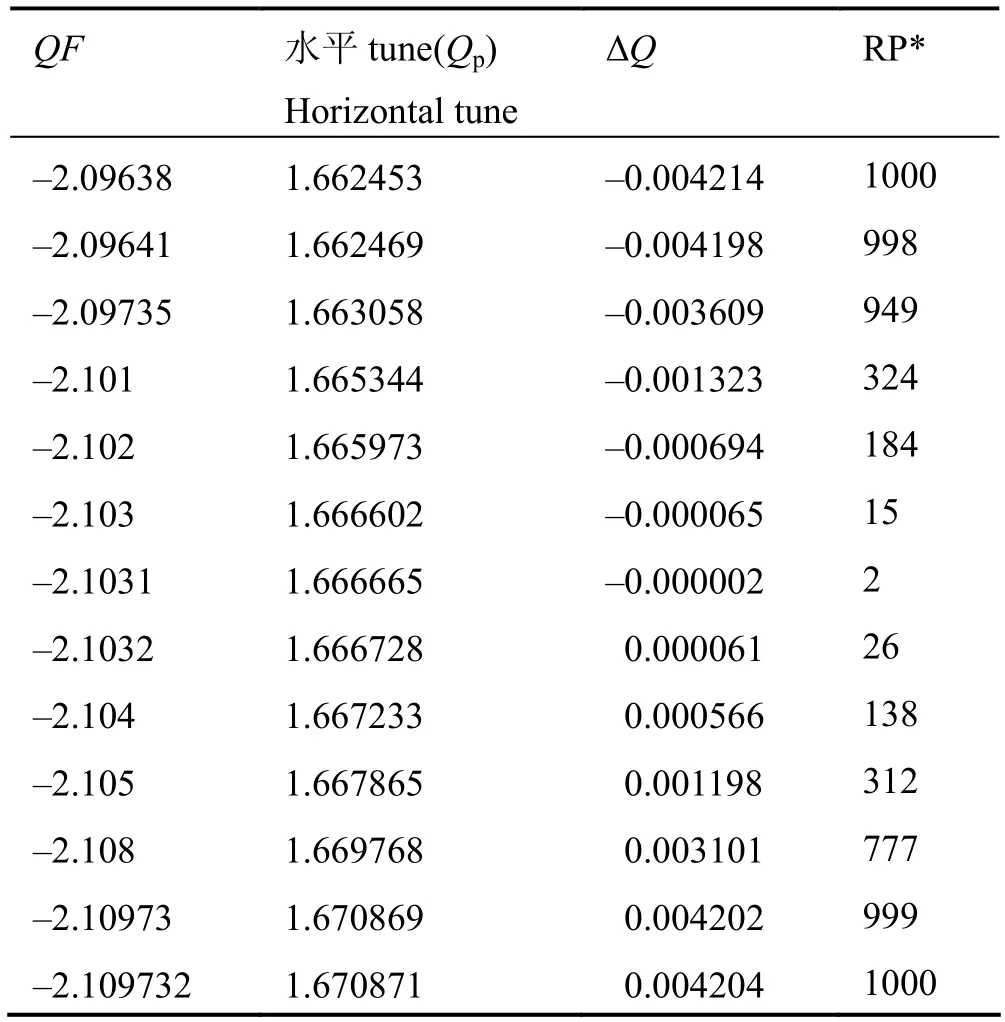
表1 四極磁鐵強度變化引起的各參數變化(S不變，總共1000個粒子)Table 1 Parameters under different strengths of the quadrupoles (fixed S, extracted beam of 1000 protons).

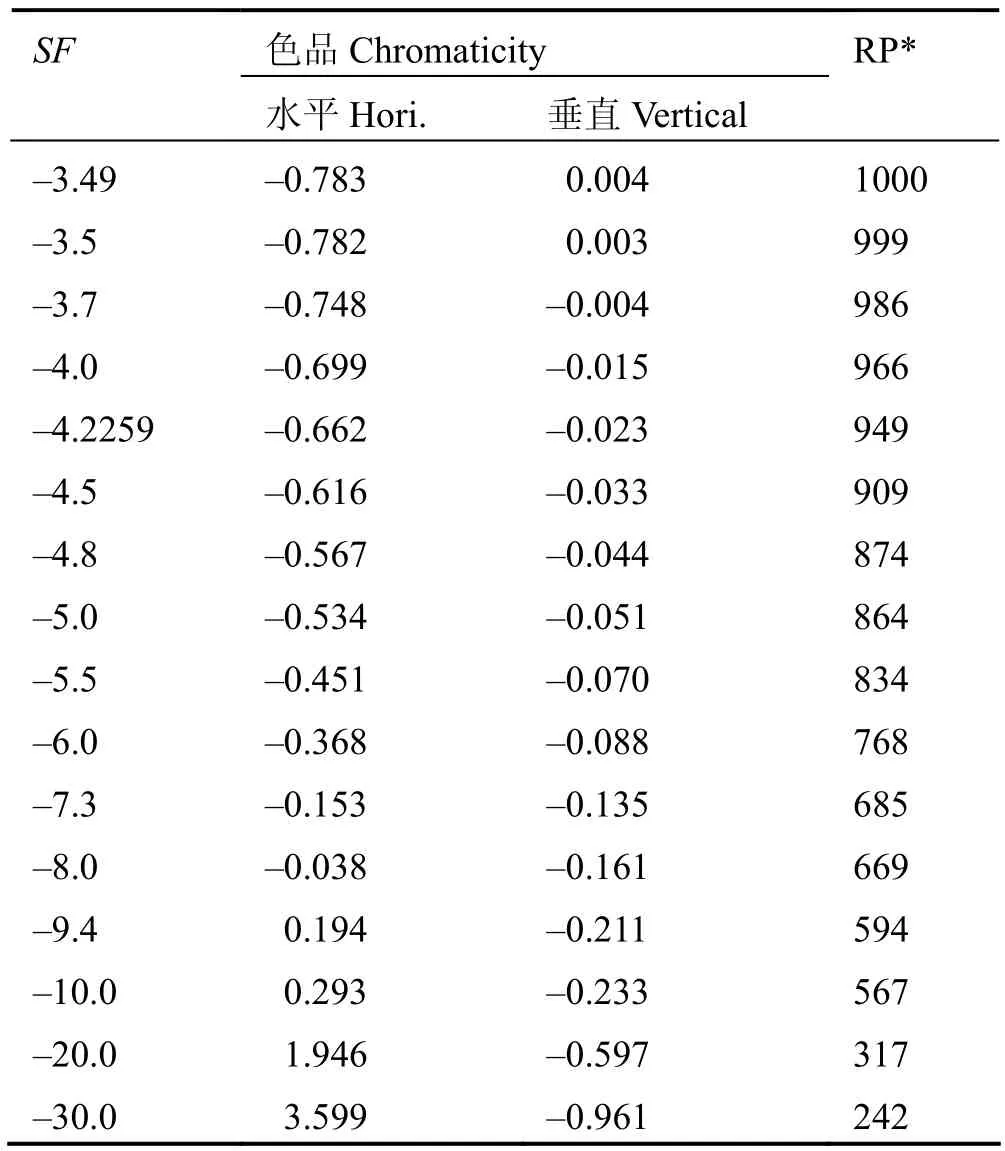
表2 六極磁鐵強度變化引起的各參數變化(ΔQ不變，總共1000個粒子)Table 2 Parameters under different strengths of the sextupoles (fixed ΔQ, extracted beam of 1000 protons).

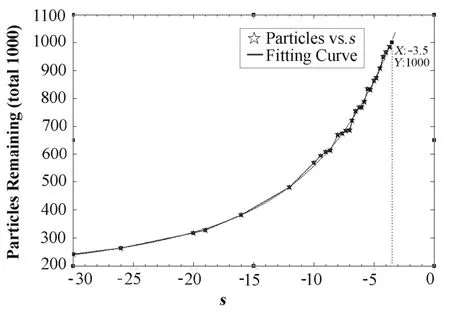
圖5 引出粒子的原始曲線與擬合曲線Fig.5 The original curve and fitting curve of extracted particles.

4 結語

應用Hamiltonian理論，分析了醫用質子加速器慢引出RFKO方法的基本原理，解析了RFKO方法的振幅增長機制；分析了為使束流幅度達到一定均勻性的幅度調制(AM)函數模型，由此導出不同RFKO踢角和引出束流的關系以及為達到束流均勻引出時踢角隨時間變化的關系。

運用軟件WinAGILE模擬了初始粒子動量分布與引出束流分布的關系；tune值偏差及共振驅動六極磁鐵與引出束流的關系。模擬結果較好驗證了理論分析，對醫用質子加速器慢引出RFKO調束具有一定指導意義。

1 Sato S, Furukawa T, Noda K. Dynamic intensity control system with RF-knockout slow-extraction in the HIMAC synchrotron[J]. Nucl Instr Meth, A, 2007, 574: 226–231

2 Noda K, Furukawa T, Shibuya S,et al. Source of spill ripple in the RF-KO slow-extraction method with FM and AM[J]. Nucl Instr Meth, A, 2002, 492: 241–252

3 Accelerator complex study group. Proton-Ion Medical Machine Study (PIMMS) Part I [R]. Geneva, 1999

4 劉乃泉. 加速器理論[M]. 第2版. 北京: 清華大學出版社, 2004: 49–58 LIU Naiquan. Accelerator theory[M]. Second ed. Beijing:Tsinghua University Press, 2004: 49–58

5 Noda K, Kanazawa M, Itano A,et al. Slow beam extraction by a transverse RF field with AM and FM[J].Nucl Instr Meth, A,1996, 374: 269–277

6 Furukawa T, Noda K, Muramatsu M,et al. Global spill control in RF-knockout slow extraction[J]. Nucl Instr Meth, A, 2004, 552: 196–204

7 Bryant P J. AGILE program for synchrotron lattice design[OL]. http: //nicewww.cern.ch/～bryant