基于小波變換的二通道數據采集濾波器組設計

王 飛，鄧志清

（1.船舶重工集團公司723所，揚州225001；2.鎮江艦艇學院，鎮江212001）

0 引 言

在處理超寬帶信號時，信號帶寬過大，為降低對A／D采樣的要求，可以考慮將信號分解為二通道或者多通道情況進行分別采樣，從而實現降速采樣的目的。小波變換的特點就是將信號在不同尺度上進行分解，通過小波的帶通濾波特性實現對信號頻帶的分割。采用小波變換理論對信號進行逐層分解和重構，逐步降低信號的頻率分析區間，為構造多通道采樣系統提供了一種思路。

1 二通道采樣系統

為了分析方便，采用倒推的方法，假設二通道采樣系統（如圖1所示）已經建立起來，然后討論濾波器設計所要達到的條件［1］。

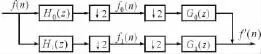
圖1 二通道采樣系統信號流程示意圖

圖1中f（n）為采樣序列，f′（n）為處理后前者的估計，H（z）和G（z）分別為分解和重構濾波器。H0（z）為低通濾波器，H1（z）為高通濾波器，后者依此類推。由圖中的信號流程，可以得到以下關系：

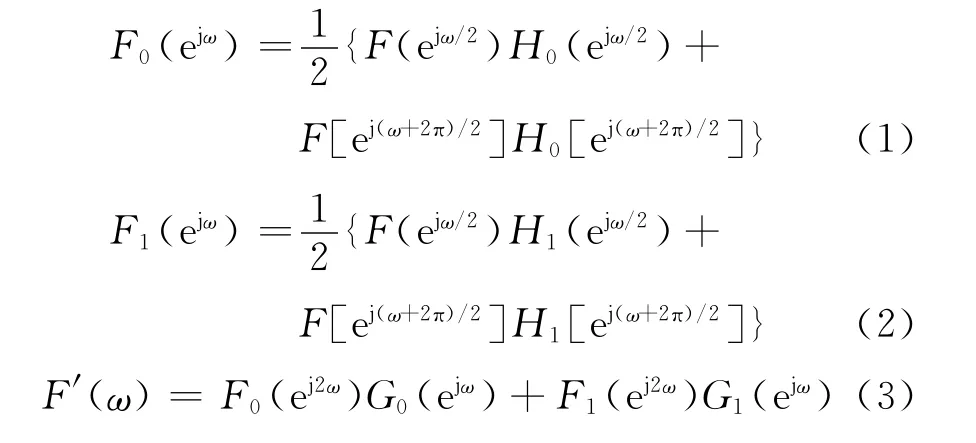
將式（1）和（2）代入式（3）中，得：

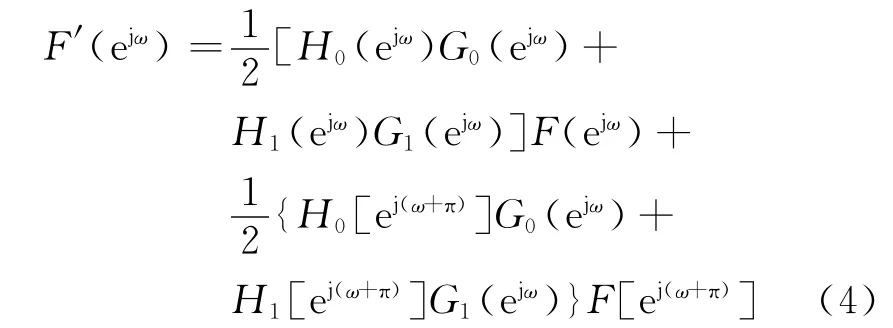
式（4）右邊第1項表示信號頻譜，第2項表示由于對信號的抽取和插零所帶來的頻域混迭。若將第2項清零，則混迭可以消除，即有：

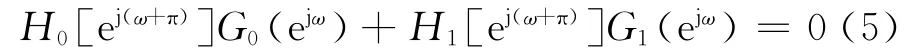
式（6）為滿足式（5）條件的1組關系：

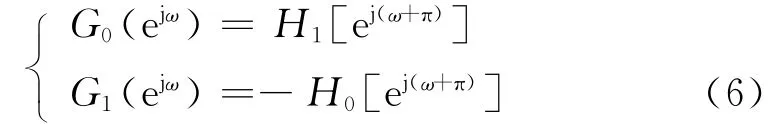
在分解濾波器中，低通濾波器和高通濾波器相位上可有一定的關系，即：

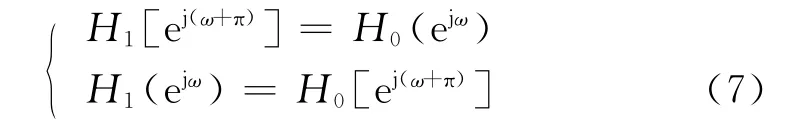
這樣是為了使分解的低通和高通濾波器有正交性，只要取適當的濾波器函數就可以做到這一點。式（7）對應于時域的關系為：

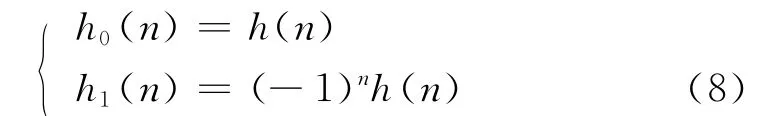
將式（6）和（7）代入式（4），可以得到系統輸入輸出之間的關系式：

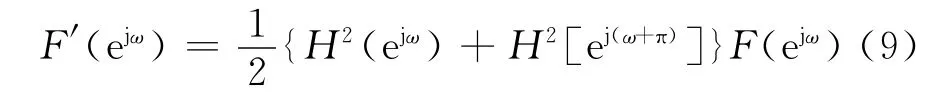
式（9）給出了1個消除幅度失真的條件，只要右邊前一項為1，即：

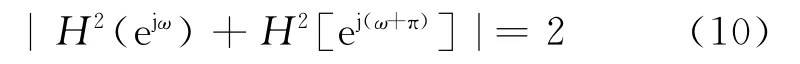
圖2 二通道采樣系統示意圖

圖2中，只要f′0（n）、f1（n）′和f0（n）、f1（n）是相同的序列，就可以保證f′（n）是f（n）的估計。這需要兩路D／A和A／D時鐘同步，且都以頻率f進行采樣，假定采樣是理想的，即使f′0（n）與f0（n）出現相位不一樣的情況，并不影響數據的重構，因為后期處理的時候可以將f0′（n）做1次相位的調整即可。抽取的過程類似于降頻，每隔1個輸入樣點取1個 樣本，即得到序列f′0（n）。以f／2為采樣速率取代抽取的過程，即得到圖3所示關系。

圖3 采樣率為f／2的二通道采樣系統示意圖

在D／A帶寬足夠大的情況下，上圖的2路D／A可以放在濾波器處理之前，即：

圖4 采樣一路D／A的二通道采樣系統示意圖

上圖中AH0（z）是對應 H0（z）的模擬濾波器，AH1（z）同理。進一步，若滿足：

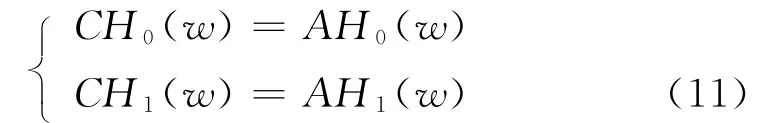
則二通道的采樣設計原理如圖5所示。

圖5 二通道采樣結構圖

圖5中D0（n）和D1（n）對應f′0（n）和f′1（n），s（n）對應f′（n），至此，基于二通道的數據采樣框圖設計完成，并且通過理論分析，在采樣率為f／2的情況下，依然可以得到原始信號的重構信息。在整個設計過程中，并沒有要求分解和重構濾波器具有理想的過渡帶，這就保證了模擬濾波器CH0（w）、CH1（w）可以更好地逼近數字濾波器 H0（z）和H1（z）。

這樣，通過設計滿足式（5）、（7）和（10）條件的數字低通濾波器H（ejω），經過二通道采樣系統可以得到輸出s（n），在存在相位失真的前提下，完成對信號f（t）的采集和重構，但是滿足條件的低通濾波器并不好設計。

2 基于Daubechies小波的二通道采樣系統

根據小波理論，對任意給定的消失矩階數p，Daubechies小波［2］有最小的支集，而緊支集小波可由有限脈沖響應共軛鏡像濾波器h計算得出［3］。假設有實的因果濾波器h［n］，那么＾h（h的傅里葉變換）可以表示為這樣一個三角級數：

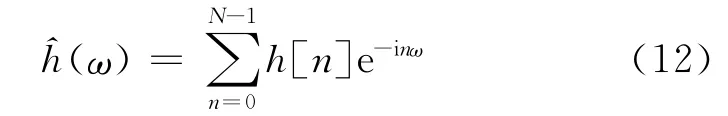
小波的k階消失矩定義為：

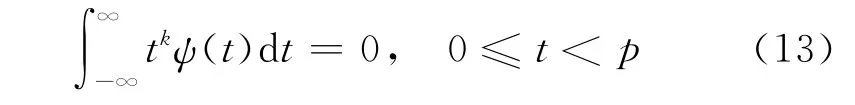
為保證小波有p階消失矩，需要＾h在ω＝π處有p重零點，這樣式（12）可以構建為：

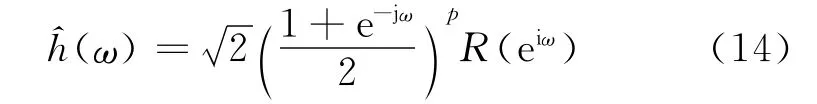
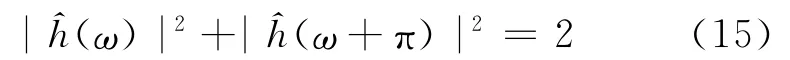
那么有限脈沖響應濾波器h［n］就可以得到，并且h的非零個數N＝m＋p＋1。根據Daubechies給出的證明，實共軛鏡像濾波器h，如果使得＾h在ω＝π處具有p重零點，則它至少有2p個非零系數。

Daubechies濾波器h［n］在數學上有更簡潔的表達方式，即：

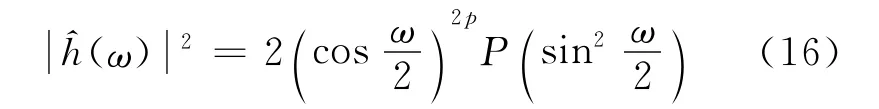
其中右邊后一項是一多項式，表示｜R（e－iω）｜2。以db4小波為例，給出它的濾波器。

為了更好地理解db4小波的濾波原理，圖6就幅頻曲線做出說明。

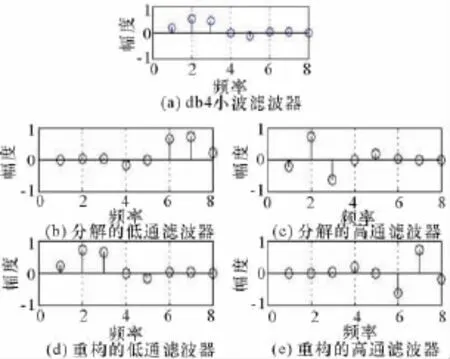
圖6 db4小波濾波器及分解和重構濾波器

由圖7可以很明顯地看出曲線在一定的頻率區間外迅速出現衰減，所以小波具有帶通的濾波效果。

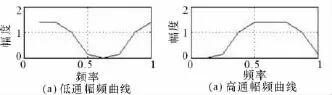
圖7 db4小波低通濾波器和高通濾波器幅頻特性曲線

比較式（10）、（15）和（16）可以發現它們的系數是相同的，式（10）和式（15）形式上也可以基本上等同。這已經給出了一部分構建二通道濾波器的答案。為了更好地理解小波是如何構建正交鏡像濾波器的原理和多分辨率分析理論，下文將詳細分析小波和濾波器組的關系。

數學上常用“空間”的概念來論述多分辨率分析的完備性，將空間Vj和 Wj的規范正交基 ｛φj，n｝n∈z和 ｛ψj，n｝n∈z在2個空間的信號投影表示為：

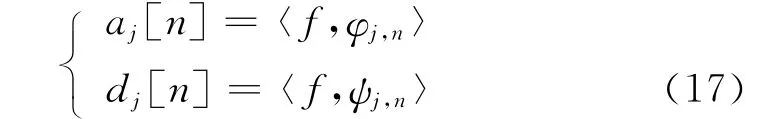
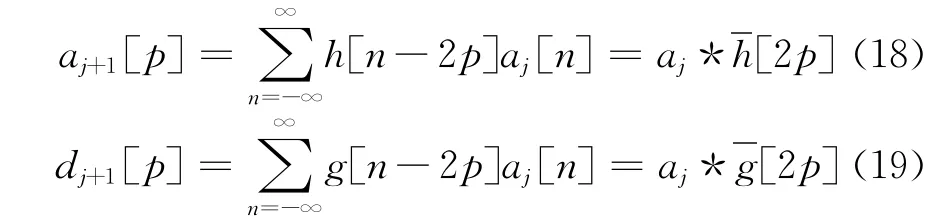
小波重構為：

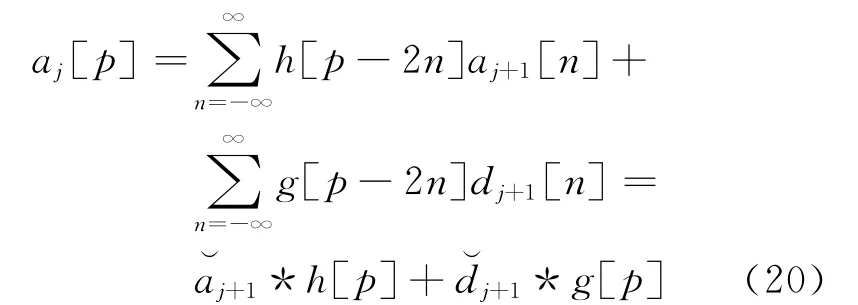
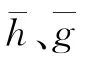
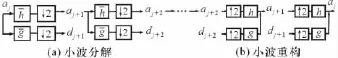
圖8 小波分解和小波重構

雙通道濾波器組將信號a0和低通濾波器h、高通濾波器g做卷積，并對輸出做因子為2的子采樣；然后用對偶低通?h和高通?g濾波器對零擴充信號濾波，可得到重構信號，如圖9所示。其關系為：

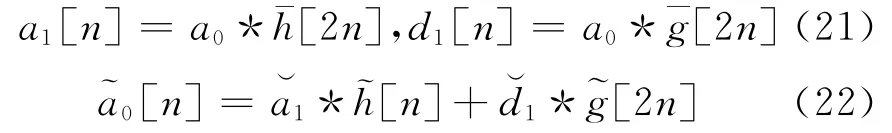
圖9 雙通道低通和高通濾波器的分解和重構

圖9和第1節中推導的二通道信號流程圖已經非常相似了，這里只需要將小波的雙通道分解和重構與上節中涉及到的低通和高通濾波器對應起來就可以在理論上完全等同起來。也就是說滿足小波雙通道的濾波器組完全可以滿足二通道采樣系統的要求。實際上對于小波雙通道濾波器組能夠精確重構信號的充要條件已經由Vetterli［4］給出：

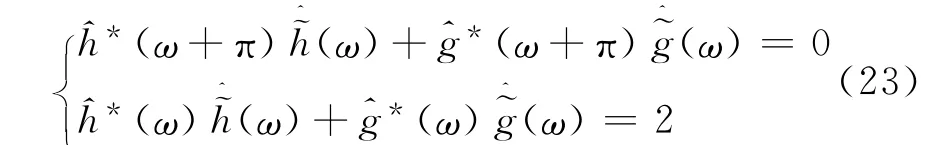
通過濾波器組矩陣滿足仿酉性質［5］，Vaidyanathan將上述充要條件推廣到M（M為自然數）個通道的多速率濾波器組。Smith和Barnwell以及Mintzer根據前人的結論給出了共軛鏡像濾波器的定義條件：

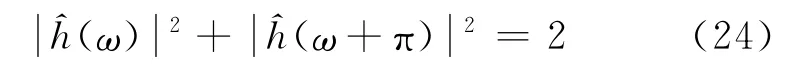
這個條件也是生成正交小波的條件之一。經過多位學者的努力，Daubechies系小波已經具備上述的充要條件。通過以上分析，可以歸納為：首先，二通道采樣系統對信號降頻采樣是可以理論構建的，通過理論推導的濾波器組相互之間需要滿足一定的條件；其次，小波分解和重構的理論基礎是完備的，其關于正交鏡像濾波器組的構建方式，非常契合于前文推導的二通道采樣濾波器組應該滿足的關系；第三，通過調用已經存在的小波基函數，滿足相應的條件下，理論上可以達到對信號降頻采樣的目的，采樣頻率要求為原來的一半，這非常有利于超寬帶信號的采集，有利于降低對ADC器件的硬件要求。

3 仿真驗證

為驗證基于小波的正交鏡像濾波器組的有效性，用db4小波對一個超寬帶沖激信號進行二通道采樣處理，結果如圖10所示，結果展示了信號經小波濾波器一層分解后的兩路信號形式，并進行重構，重構誤差的數量級很小，不影響信號的后續處理。

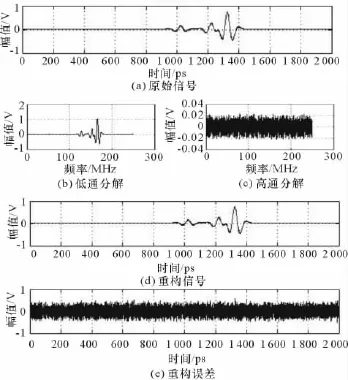
圖10 db4小波分解重構圖

圖10說明：使用二通道采樣原理構建小波，并使用相關小波對信號做一次分割即二通道采樣處理，能較精確地均分頻帶，重構效果良好，誤差較小。

4 結束語

本文研究了二通道數據采集系統的原理，分析了Daubechies小波與二通道數據采集系統中濾波器組的關系，采用db4小波重構了低通、高通濾波器，最后用MATLAB仿真驗證了采用db4小波對一個超寬帶沖激信號進行二通道重構處理的結果。仿真結果表明重構效果良好，誤差較小。

［1］黃柯宇.基于小波的UWB雷達信號采集及頻帶分割濾波器研究［D］.成都：電子科技大學，2003.

［2］高成.Matlab小波分析與應用［M］.北京：國防工業出版社，2007.

［3］Stephane Mallat.信號處理的小波導引［M］.楊力華，戴道清，黃文良，湛秋輝譯.北京：機械工業出版社，2002.

［4］Vetterli M.Fliter banks allowing perfect reconstruction［J］.Signal Processing，1986，10（3）：219－244.

［5］Akansu A N，Haddad R A，Caglar H.The binomial QMF－wavelet transform for multire－solution signal decomposition［J］.IEEE Transactions on Signal Processing，1992，6（5）：250－261.