基于穩健初值的抗差估計在公共點選取中的應用

肖玉兵,曾凡永,劉 毅,郭騰龍

(1.江蘇省水文水資源勘測局南通分局,江蘇南通226006;2.河海大學地球科學與工程學院,江蘇南京210098)

0 引 言

坐標轉換中經常使用最小二乘法求解轉換參數,但是傳統的最小二乘法適用于正態分布的樣本,在數據含有較多量值不大的隨機性誤差情況下較為理想,但對偏離主體分布的粗差不夠敏感[1]。因此,坐標轉換前首先要對公共點進行篩選,剔除含有粗差的坐標值。一般的做法是首先對含有粗差的樣本點進行最小二乘平差,以最小二乘的殘差估值作為初值進行抗差估計,利用迭代終止時的等價權值判斷粗差的位置。但這樣做的問題是,含有粗差的最小二乘估值與真值存在較大的偏差,以此作為初值進行抗差估計,必然會對粗差的定位產生影響。

本文以具有穩健性的L1范數最小法為基礎,驗證基于穩健初值的抗差估計理論在公共點粗差定位方面的可靠性和準確性。

1 抗差估計

抗差估計法屬于粗差探測理論中的“方差擴大”模型的方法,即將粗差歸入隨機模型,含粗差的觀測值可以看作與其他同類觀測值具有相同的期望,但粗差觀測值的方差將異常的大。抗差估計常用的方法是選權迭代法,與傳統最小二乘法不同的是,選權迭代法的權是以改正數v為自變量的等價權函數[2-3]。選權迭代法的函數模型為:

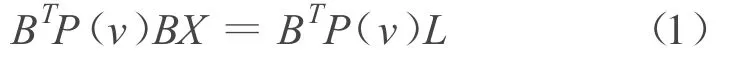
式中:P(v)應滿足一定的條件,使正常觀測值在迭代結束時的權不變,而含有粗差的觀測值的權趨近于零,以降低含有粗差的觀測值對平差結果的影響,并達到定位粗差的目的。根據權函數的不同,有不同的抗差估計方法,部分列舉如下:

1.1 Huber法

Huber法的極值準則是假設觀測值在不利分布情況下求最優估計,其計算公式為:

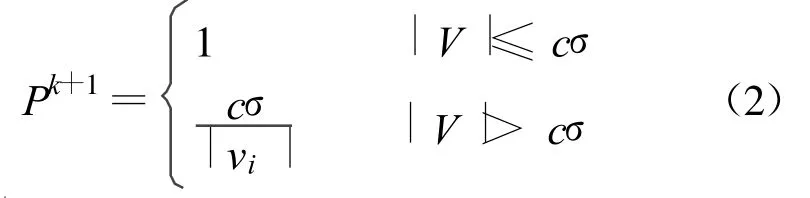
式中:Pk+1為第k+1次迭代的權函數,σ為單位權中誤差,vi為觀測值殘差,c為常數,通常c取值在0.7至2.0。

1.2 帶權數據探測法

帶權數據探測法由EL-HAKIM提出,其計算公式為:

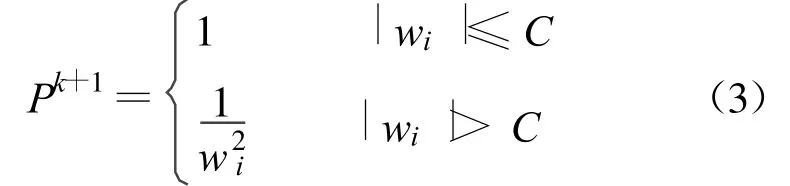
1.3 驗后方差估計選權迭代法

驗后方差估計選權迭代法思想是[4-5]:根據經典的最小二乘平差,求出觀測值的驗后方差,再利用方差檢驗找出方差異常大(即粗差)的觀測值,然后給予它一個相應小的權進行下一次迭代平差,逐步實現粗差的定位。對于一組等精度觀測值,構造式如(4)的統計量和式(5)的相應的權函數:

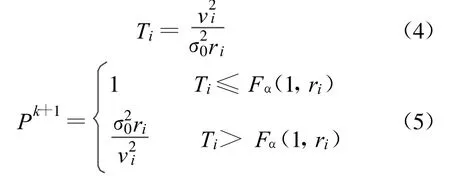
式中:σ0為單位權中誤差;ri為相應的多余觀測數;Fα(1,ri)為F分布的上α分位點。

2 具有穩健初值的抗差估計

選權迭代法的關鍵是權函數殘差初值的確定,常用的做法是根據傳統的最小二乘平差來確定。但是由于最小二乘估計對粗差具有均衡作用和不敏感性,有粗差的觀測值的殘差并非最大,致使選權迭代時發生錯誤的判斷,當數據中的粗差較多時尤為明顯[6-7]。因此應該采用一種穩健的估值方法,計算觀測值的殘差,提高粗差定位的穩定性。L1范數最小法的求解實際是如式(6)的線性規劃問題:

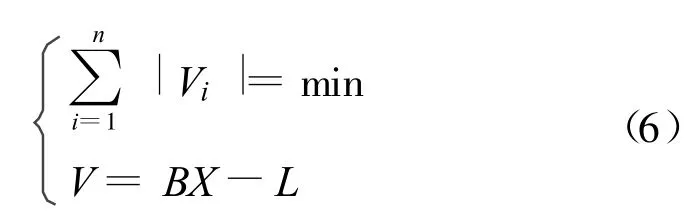
式中:X表示誤差方程式的待定參數,V表示觀測值的改正數。由于線性規劃具有較好的穩健性,因此可利用線性規理的單純形法求解式(6)的最佳可行解。根據最佳可行解計算坐標轉換模型的殘差V,作為抗差估計的初值,利用選權迭代法定位含有粗差的公共點位置。

3 計算實例

試驗以某地區工程控制網為例,該區域中共有控制點12個,已知其54和80高斯平面直角坐標,為了驗證本文所提方法的可靠性與準確性,選取其中五個控制點進行分析,將其編號為1,2…,5,點位分布如圖1所示。坐標轉換模型為式(7)所示的相似變換模型,并選取全部公共點參與計算。

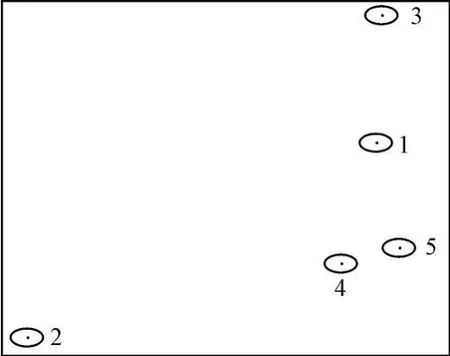
圖1 公共點點位分布

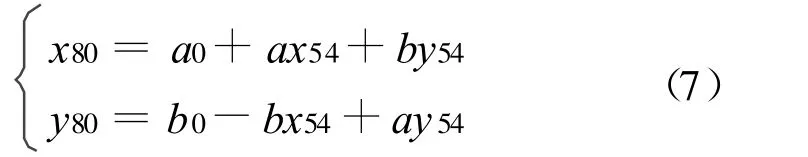
式中,(x54,y54)、(x80,y80)分別為公共點的54和80高斯平面直角坐標。為驗證“具有穩定初值的選權迭代法”對公共點中粗差值定位的可靠性,設計了如下五種方案進行粗差定位的實驗:

方案1:在5號點的Y坐標中加入-2 cm粗差;

方案2:在2號點的X坐標中加入-2 cm粗差;

方案3:在3號點的X坐標加入-25 cm,在4號點的Y坐標加入+20 cm的粗差;

方案4:在1號點的X坐標加入+20 cm,在5號點X坐標加入-60 cm的粗差;

方案5:在2號點的Y坐標加入+5 cm,在4號點的X坐標加入+10 cm的粗差。

以抗差估計中的帶權數據探測法為例,分別以基于最小二乘初值和基于穩健初值的抗差估計法,對上述方案中的粗差進行定位。

以含有粗差的公共點坐標為觀測值,以式(7)為數學模型,依次對上述方案采用經典最小二乘法進行平差,得到如表1所示的殘差,并以該殘差作為權函數的初值,采用帶權數據探測法迭代求解,得到的等價權的最終形式如表2所示。其中表2的最后一列表示粗差定位的結果(“T”表示粗差定位成功,“S”表示只定位出一部分粗差,“F”表示粗差定位失敗)。表2的最后一行列出了相應觀測值的多余觀測分量。

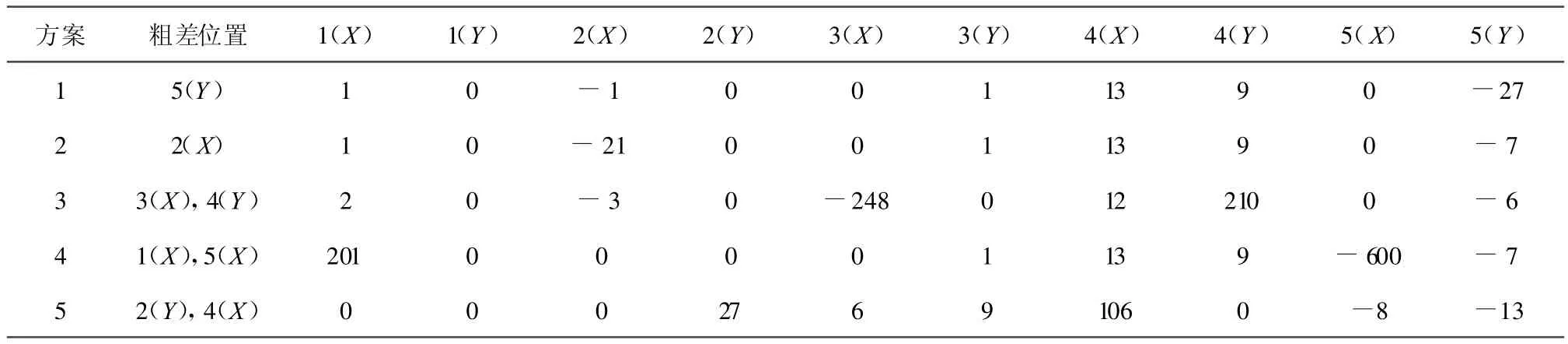
表1 L1范數最小法的轉換殘差(mm)

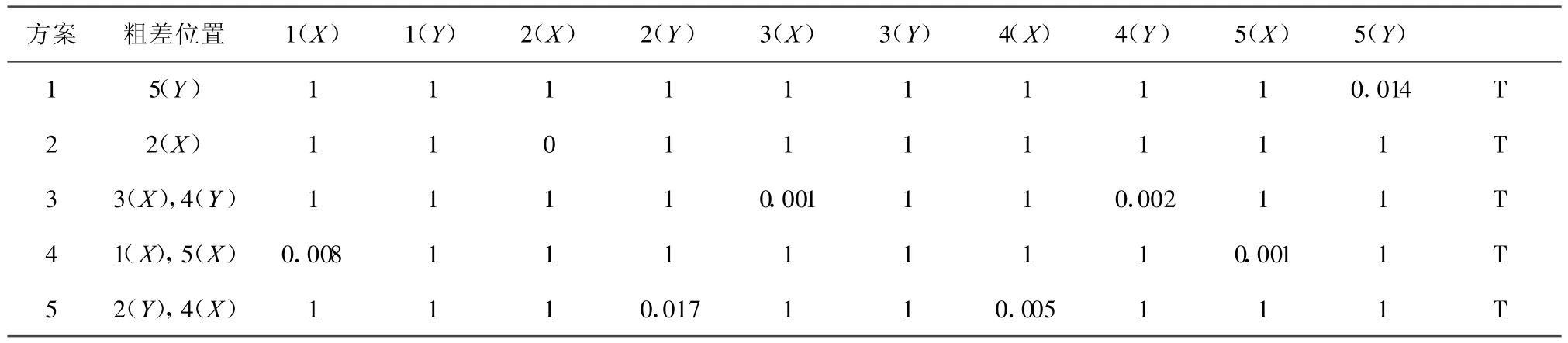
表2 基于穩健初值抗差法的等價權最終形式

分析表1可知,觀測值的粗差集中反映在平差后的相應殘差上,無粗差的觀測值改正數則相對較小。如方案4,含有粗差的觀測值為1號點的X坐標和5號點的X坐標,其改正數分別為201 mm和-600 mm,基本反映了其自身粗差值的大小,而無粗差的觀測值的改正數最大只有13 mm,受粗差影響較小。

以上分析說明L1范數具有良好的穩健性,因此以L1范數的改正作為權函數的初值,進行迭代求解,如表2所示,具有粗差的觀測值的權接近于0或是與其他觀測值的權相差較大,取得了良好的定位效果。

4 結 語

抗差估計法定位能力的強弱與權函數的初值有很大的聯系,如果權函數的殘差初值能較準確地反映粗差的狀況,選權迭代法的粗差定位能力將會有很大的提高。具有穩健初值的抗差估計在增加權函數初值穩定性的基礎上,提高了系統的粗差定位能力。通過以上分析與比較,說明了在坐標轉換中L1范數具有較高的穩健性,驗證了基于穩健初值的抗差估計法在粗差探測方面的可靠性與準確性,因此,在坐標轉換前利用該方法對公共點進行篩選具有較高的實用價值。

[1]景 繼,王 建.基于抗差最小二乘的水工監測數據粗差探測[J].水電能源科學,2007,26(6):81-84.

[2]席志芳,樓 宇.實用性粗差檢測和定位的研究[J].工程勘察,1995,(6):52-55.

[3]陳西強,黃張裕.抗差估計的選權迭代法分析與比較[J].測繪工程,2010,19(4):8-11.

[4]李德仁.利用選權迭代法進行粗差定位[J].武漢測繪學院學報,1984,(1):47-67.

[5]孫同賀,閆國慶.基于驗后方差估計原理探測與剔除粗差[J].海洋測繪,2011,31(5):28-30.

[6]李 鵬.高程測量粗差探測方法與高程控制網穩定性分析[D].南京:河海大學,2005.

[7]林國慶,范東明.帶權最小絕對值和法在粗差探測方面的應用[J].測繪,2010,(1):18-21.