液艙晃蕩載荷數值模擬中的流固耦合影響研究

徐國徽，顧學康

（中國船舶科學研究中心，江蘇 無錫 214082）

1 引 言

近年來隨著液化天然氣（LNG）需求的增加，液化天然氣船船體和液艙主尺度不斷大型化。大型化后的LNG船載貨量一般為25-35萬立方，幾乎為傳統型LNG船的兩倍。由于吃水限制，液艙主要增加長度和寬度。因而船體運動引起的液化天然氣的晃蕩運動及其對液艙結構的沖擊問題越來越突出，部分裝載的需求也越來越高[1]。液艙部分裝載時，船體大幅晃蕩引起的沖擊壓力對艙室結構和圍護系統可能造成嚴重破壞，此問題已經引起了研究和設計者們的廣泛關注。另外，由于液艙邊界的彈性圍護系統的存在，大型LNG船艙內液貨大幅晃蕩運動時作用在艙壁上的沖擊壓力將受到艙壁彈性的影響，導致晃蕩載荷和結構響應與剛性艙壁情況會有所不同。因此就液艙晃蕩中的流固耦合問題開展數值計算方法的研究具有明顯的工程實用意義，國內外已有學者展開了相關問題的探索性研究。

朱仁慶[2]采用自編程序將流場通度的概念、VOF法與水彈性力學理論相結合，進行了二維粘性流體與彈性結構耦合作用的理論與分析方法研究。Zhu等[3]應用處理粘性流體晃蕩與彈性結構相互耦合作用的理論及相應數值計算方法，流體運動采用N-S方程描述，控制方程采用有限差分法離散，并由超松弛迭代法求解，液體自由表面通過流體體積法進行重構，考察二維液艙不同結構剛度對液體晃蕩的影響。娜日薩[4]在DNV基于壓力的液艙晃蕩仿真及結構強度評估方法的基礎上，引入時空放大、體積模擬減縮等技術提出了耦合的VLCC液艙晃蕩仿真及強度評估方法。Rognebakke和Faltinsen[5]考慮液體內空泡和結構的水彈性效應，采用數值方法研究了部分充滿的矩形罐的誘捕空氣（entrapment of air）和水彈性問題。Wang和Kim[6]采用聲固耦合分析法和簡單的二維聲固耦合模型研究結構響應的水彈性效應。Hisashi等[7]結合ALE方法做局部沖擊分析，計算貨艙系統的結構響應。目前液艙流固耦合問題的研究還處于初步階段，學者們的方法基于不同的條件假設和理論，得出的結果和論斷也各有差異。

本文研究大型LNG船液艙晃蕩中的流固耦合效應，采用基于顯式時間積分方法的有限元/有限體積法程序DYTRAN模擬流體和結構的運動和變形及其相互作用，從二維剛性模型開始，以計算流體力學方法結果和試驗結果作為參照進行數值方法研究和參數分析，進而建立三維剛性和彈性液艙兩種模型，比較不同模型的數值計算結果，得到了對大型LNG船液艙晃蕩載荷和強度評估具有參考價值的結論。

2 耦合理論介紹

依據耦合機理，如果耦合作用僅僅發生在兩相域的交界面上，在方程上的耦合是由兩相耦合面的平衡和協調關系引入的。對于這類問題按其兩相間相對運動的大小及相互作用的性質又可分為三類[8]:一是流體和固體結構之間有較大的相對運動。如機翼顫振或懸橋震蕩中發生的氣動耦合問題，習慣上稱為氣動彈性力學問題；二是具有流體有限位移的短期問題。流固相互作用是在瞬間完成的，其特征是流體的密度發生急劇變化，如液體中的爆炸與沖擊問題；三是液體域與固體域的動力相互作用。其特點是流固相互作用時間較長，相對位移有限，習慣上稱為液動彈性力學問題，如近海結構對波浪或地震的響應、充液容器的晃動問題、壩水、船水耦合響應以及水力機械在流體介質中的振動問題；本文所研究的晃蕩問題就屬于第三類問題。

流固耦合問題按其研究方法可分為弱耦合法和強耦合法，或分別稱之為分區迭代求解法和直接求解法。所謂弱耦合法是對流體域和固體域分別建立和求解運動方程，兩個運動方程間則通過插值函數進行流體壓力、結構位移等的數值傳遞，從而實現流體和結構的相互耦合。采用弱耦合方法時，流體和結構用各自的求解器在時域上積分，交錯時間推進，這種方法能充分利用現有的計算流體動力學和計算結構動力學的方法和程序，只需作少量的修改，從而保持各程序的模塊化特性。它的主要缺點是由于積分是交錯進行的，流體和結構的時間推進積分總是存在時間滯后，耦合界面上的能量不能保持守恒，無法滿足動平衡。強耦合法則是對流體和結構分別建立運動方程，采用數值方法將兩個方程耦合起來形成同一控制方程即耦合方程，在單一時間步內，同時求解耦合界面的壓力分布以及結構對壓力做出的響應，避免了弱耦合法中出現的時間滯后問題。顯然，強耦合法能夠準確地描述流體的運動，更真實地反映流體和結構的相互作用，理論上更加合理，分析過程更加嚴密。但由于強耦合理論的復雜性以及計算機軟硬件資源的限制，該方法適合求解沒有接觸分析的小型到中型的瞬態耦合問題。晃蕩屬于典型強耦合問題，需要同時求解流體運動和結構的響應。

流固耦合問題的計算方法應用較多的有三類:

（1）固體和流體均采用修正拉格朗日法

此法優點是編程方便，即用一種方法可對流固兩種介質進行分析。對不可壓流體相關的流固耦合問題，此類解法相當簡便。商業軟件多采用此方法處理簡單的不可壓流體與固體的相互作用問題。缺點是對可壓縮流場相關的流固耦合問題，尤其是當流場中出現旋渦或強間斷時，該方法將因網格變形過大或畸變，引起計算時間步長銳減，甚至直接導致計算失敗。

（2）流體采用修正的歐拉方法處理，固體采用拉格朗日方法處理

此法屬于混合法，充分發揮了歐拉方法高精度捕捉流場與拉格朗日方法準確描述結構變形的優點，但在流固界面（以下稱為內界面）的數值交換提出新的邊界條件，流場壁面邊界節點處的物理量要通過插值得到，對內邊界條件處理的精度直接影響流場求解的精度。

（3）流體采用ALE方法處理，固體采用拉格朗日方法處理

此法屬于混合法，采用ALE網格，不需要進行網格重分及物理量插值，通過流場網格移動保證在內邊界處流場與結構網格的銜接。流場內部的網格節點運動引起單元體積的變化滿足幾何守恒（Geometric Conservation Laws,GCL），內邊界求解由ALE算法保證精度不降階。

在DYTRAN程序中同時提供Lagrange和Euler求解器，既模擬結構的變形又模擬材料的流動，Lagrange網格與Euler網格之間進行耦合，從而分析流體和結構之間的相互作用。DYTRAN程序提供后兩種耦合算法，一般耦合（general coupling）屬于第二類，ALE耦合（Arbitrary Lagrange-Euler coupling）屬于第三類。一般耦合方法對規則歐拉網格提出的快速算法有較高的計算速度由于它的耦合面不需要歐拉節點與拉格朗日節點的一一對應，所以對于結構幾何形狀復雜的流固耦合問題，一般耦合建模工作較為簡單。但耦合交界面位置的計算及單元的合并增加了計算時間。ALE方法由于歐拉域的邊界是已經確定的，這避免了像一般耦合那樣不斷計算耦合面位置的過程，也可以避免為實現耦合而建立過多的歐拉單元帶來的計算量的增加，大大提高了計算的效率。ALE方法不需要流體單元的不斷合并，數值計算結果中的噪聲較少。對于像液艙晃蕩這種結構形式簡單，固定內部流體的流固耦合問題，ALE方法是比較適合的。這也是本文研究液艙晃蕩問題采用ALE法的原因。

3 數值模擬方法研究

3.1 二維剛性模型描述

為了便于比較分析，本文選取作者前期研究[8]的矩形液艙模型（圖1）及計算工況（表1）作為算例，艙室橫蕩激勵為簡諧正弦函數，以艙室幾何中心為原點。采用任意拉格朗日（Lagrange）－歐拉（Euler）耦合（ALE）算法，流體域采用歐拉六面體單元劃分，液艙結構采用殼單元劃分，兩者網格密度一致，流固耦合面上兩種網格節點空間重合，歐拉網格不再是空間固定而是隨著結構的變形而移動。耦合典型過程是:（a）歐拉材料流動引起的壓力載荷作用到結構網格上；（b）在壓力作用下對結構響應進行積分；（c）把結構的邊界位移和運動傳遞給流體；（d）更新流體動態網格；（e）流體積分，計算新的流體壓力和應力場。此耦合法避免了結構流體兩種網格之間的交叉，減少了單元合并工作量，降低了結果的數值噪聲。

表1 計算工況Tab.1 Calculation conditions

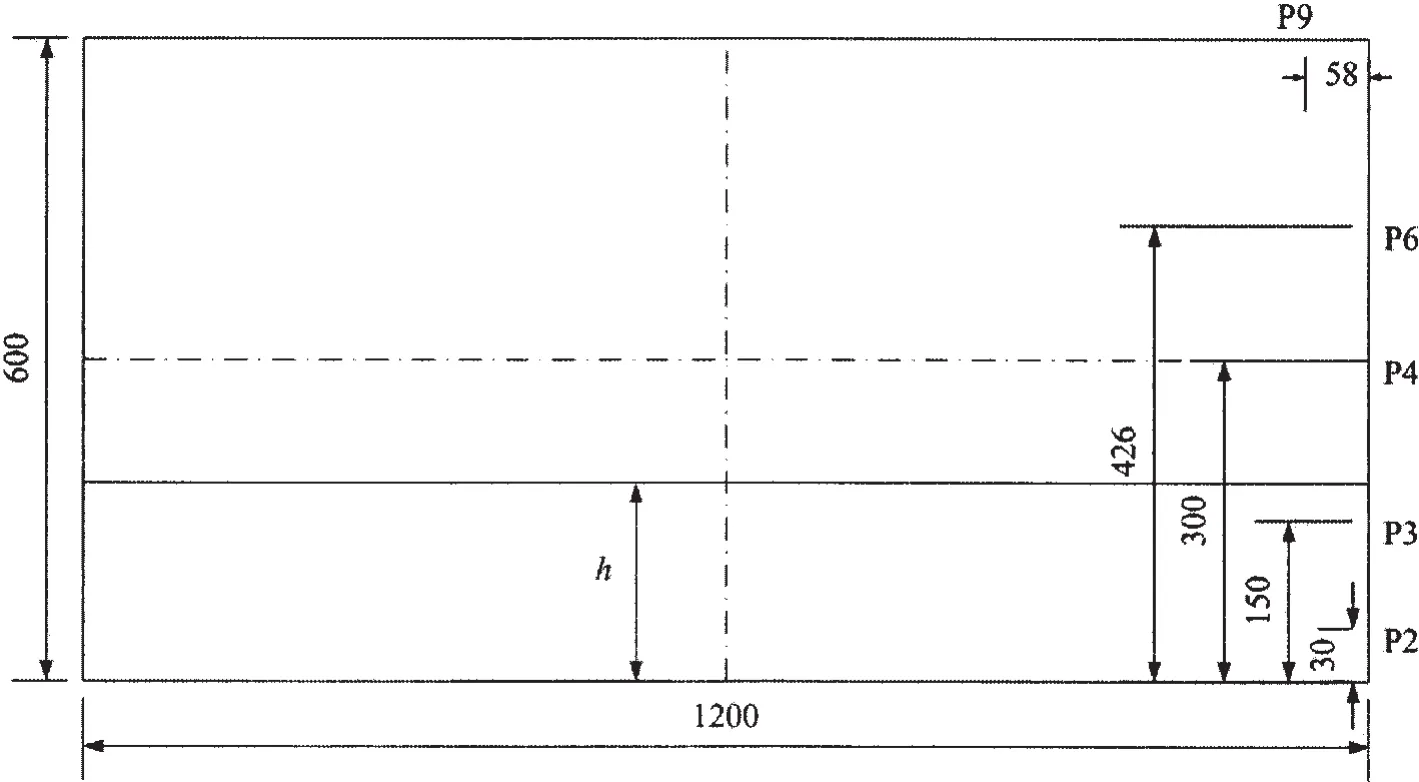
圖1 艙室幾何模型和壓力測點位置(單位mm)Fig.1 Geometrical model of the tank and pressure measuring point arrangement(mm)

圖2所示的二維模型液艙周壁為剛性材料，引用MATRIG卡片可以把Lagrange網格定義為剛體；艙內水為無粘、可壓縮線性流體本構關系材料，引用EOSPOL卡片定義；通過定義剛體質心處的強迫運動給以運動激勵，在流體的非主要運動方向設置一個單元，這樣流體僅在建模平面內運動。

DYTRAN的材料模式中，包括了線彈性、彈塑性、剛性材料、橡膠材料、低密度泡沫材料、土壤材料、正交各向異性材料、層合復合材料、率相關材料以及各種屈服準則、失效模式、狀態方程、多點爆炸燃燒模型等。

流體域采用線性流體來填充，多項式狀態方程EOSPOL定義水的多項式狀態方程，這里不計水的粘性，壓力是相對體積與比內能的多項式函數:

壓縮狀態（μ＞0）

圖2 二維剛性模型Fig.2 2D rigid model

拉伸狀態（μ≤0）

其中，μ=（ρ/ρ0）-1；ρ為水的密度，ρ0為初始狀態水的密度；e為單位質量的比內能。

忽略非線性項后可得:

其中，a1為水的體積模量。在計算的初始時刻，需定義歐拉單元的初始狀態。

對于彈性液艙的問題，所用的結構材料包括剛性材料和線彈性材料。剛體用RIGID材料，用MATRIG卡進行定義，該卡將一部分Lagrange單元定義為剛體，這一部分單元為一個剛性整體，單元之間沒有相對移動，單元本身也沒有彈性變形。該方法還可以通過定義任意幾何面為剛體，不計單元與幾何的形狀，其重量、重心和慣性矩也可以定義。

彈性體本構模型為彈性材料DMATEP，DMATEP卡只需要定義參考密度和4個彈性常數（彈性模量E、泊松比μ、體積模量K和剪切模量G）中的任意兩個就行，他們之間有如下關系:

3.2 網格更新方法

ALE耦合法的一個優點就是流體網格獨立于材料變形而進行空間運動，可以根據需要自由選擇其運動狀態，對數值分析物體的變形過程帶來了便利。不同于計算流體力學（CFD）里處理流體動邊界的動網格法和自由表面跟蹤技術VOF法，DYTRAN采用ALE方法描述帶自由液面的晃動問題時，處理計算區域內動態的網格與流體運動之間的域耦合，主要有以更新網格位置為目標和以獲得網格節點運動速度為目標的兩類網格節點速度更新方法。

Hughes（1981）等[10]提出 L-E（Lagrangian-Eulerian）矩陣法，通過對單元節點定義不同的 L-E系數與相應的流場質點速度,共同確定網格內部節點的運動；Donea（1982）等[11]提出了平均法，即用上一時刻相鄰網格點的速度平均值確定內部網格節點速度；Huerta（1988）等[12]提出了混合法，即只在自由液面或運動邊界上進行L-E網格更新，內部網格節點速度用勢流方程或代數方法計算得到。目前ALE網格更新方法都是以上述方法為基礎，其中混合法應用最廣。合理高效的網格算法可以在自由面附近獲得性態良好的計算單元，降低大幅度液體晃動計算的網格重構頻率，同時網格節點速度的數值還將影響到控制方程中對流項的量級，更重要的是改進自由液面網格節點速度的求解方案，能使ALE方法在更多樣的幾何邊界和運動邊界問題中得到廣泛應用。DYTRAN程序中在ALEGRID卡片中有一些算法，對不同問題可能需要不同的網格運動形式才適宜，否則更新過程中就會發生網格畸變。

3.3 數值噪聲控制

在動力學數值分析中，數值噪聲對計算結果有很大的影響，控制數值噪聲非常重要。設置人工粘性是為了保持計算結果的平穩性。體積粘性針對材料性質，用于控制振蕩波的形成；沙漏阻尼針對單元特性，用于避免低精度單點積分體殼單元的無剛度變形模態，提高計算精度。

3.4 時間步長控制

顯式求解方法要保證解的穩定性，求解的時間步長是隱式求解的時間步長的1/1000～1/100，即時間步長Δt必需小于應力波跨越網格中最小單元的時間:Δt=min（）。臨界時間步長Δt由單元的特cr征長度和單元的材料特點決定，不同類型的單元有其對應的算法:

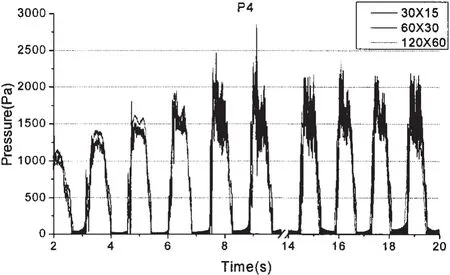
圖3 三種網格方案計算的P4點的壓力時間歷程（60%H）Fig.3 Simulated time histories of pressure P4 for three different grid schemes(60%H)

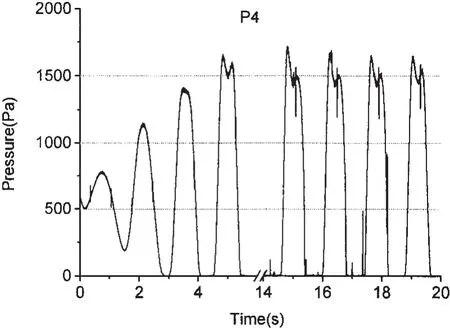
圖4 CFD計算的P4點壓力時間歷程（60%H）Fig.4 Time history of pressure P4 predicted by CFD(60%H)

上式中，Le是單元的特征長度；c是聲音在材料中的傳播速度，E是彈性模量，ρ是質量密度，σ是泊松系數，u是流體材料的速度，K是體積模量。在物理條件一定的情況下，時間步長由最小單元決定，所以在網格中盡量避免很小的單元是至關重要的。 這里采用 30×15、60×30、120×60 三套網格方案，歐拉單元特征長度分別為單位長度0.04 m、0.02 m和0.01 m。圖3為幾種網格的計算結果比較，粗網格計算速度快，但誤差造成的數值振蕩比較明顯；細網格計算用時幾乎為粗網格的十倍，精度提高的優勢也不明顯，因此中間網格（60×30）的計算方案是最有效的。與徐國徽文獻中的CFD計算結果（圖 4）及日本學者 Hinatsu（2001）模型試驗結果（圖5）相比，變化趨勢和量值十分接近，表明本文數值計算方案可以接受。

3.5 體積模量減縮

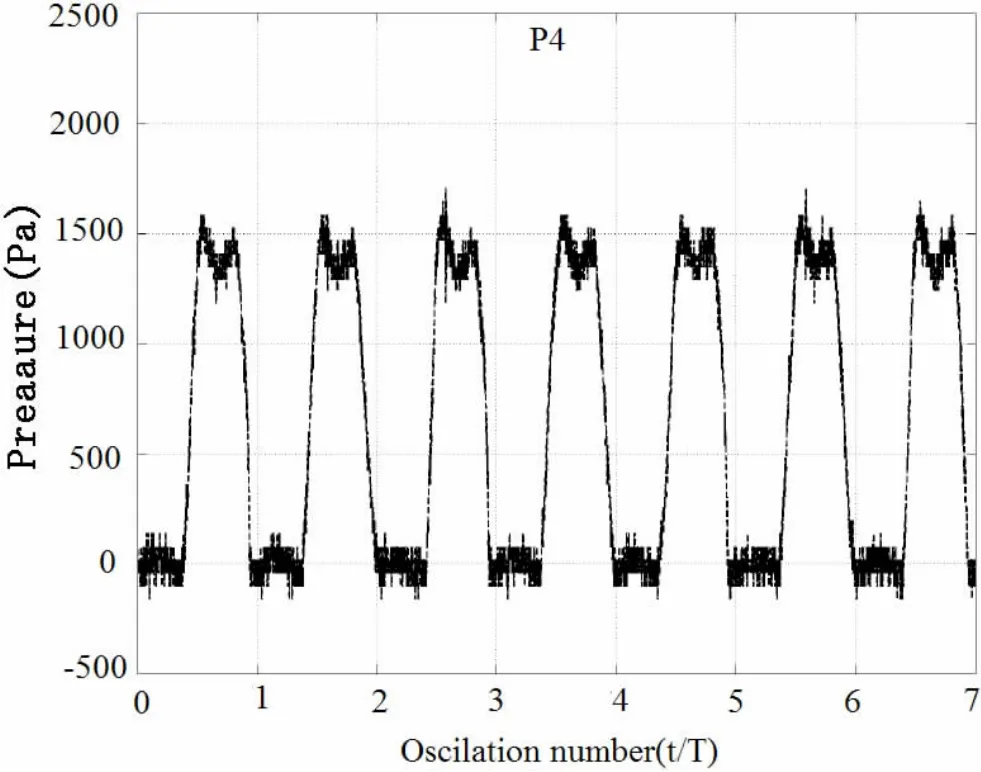
圖5 模型試驗測得P4點壓力時間歷程（60%H）Fig.5 Time history of pressure P4 measured in model tests(60%H)

為了進一步開展三維晃蕩問題的數值模擬方法研究，必須提高計算效率縮短模擬時間。根據時間步長公式，在保證計算精度歐拉網格尺寸一定的情況下，時間步長與聲波在流體中傳播速度成反比，因此為降低波速可以減縮體積模量。水的真實體積模量K=2×103MPa，圖1的二維模型中采用1800個歐拉網格模擬10個周期的晃蕩運動耗時320分鐘（計算機內存3.25 GB，Quad CPU 2.66 GHz），而當體積模量減縮為K＝2 MPa時，同樣的模擬過程僅需23分鐘，大大提高了計算效率。圖6和圖7分別是真實體積模量和減縮體積模量情況下得到的壓力時間歷程，為了相互進行比較，圖中對二者進行了高頻濾波。可以看出減縮體積模量在相當程度上減少了數值噪聲，并且壓力形式和時間特征并沒有受到影響。

圖6 P2點的壓力時間歷程（20%H）Fig.6 Time history of pressure P4(20%H)

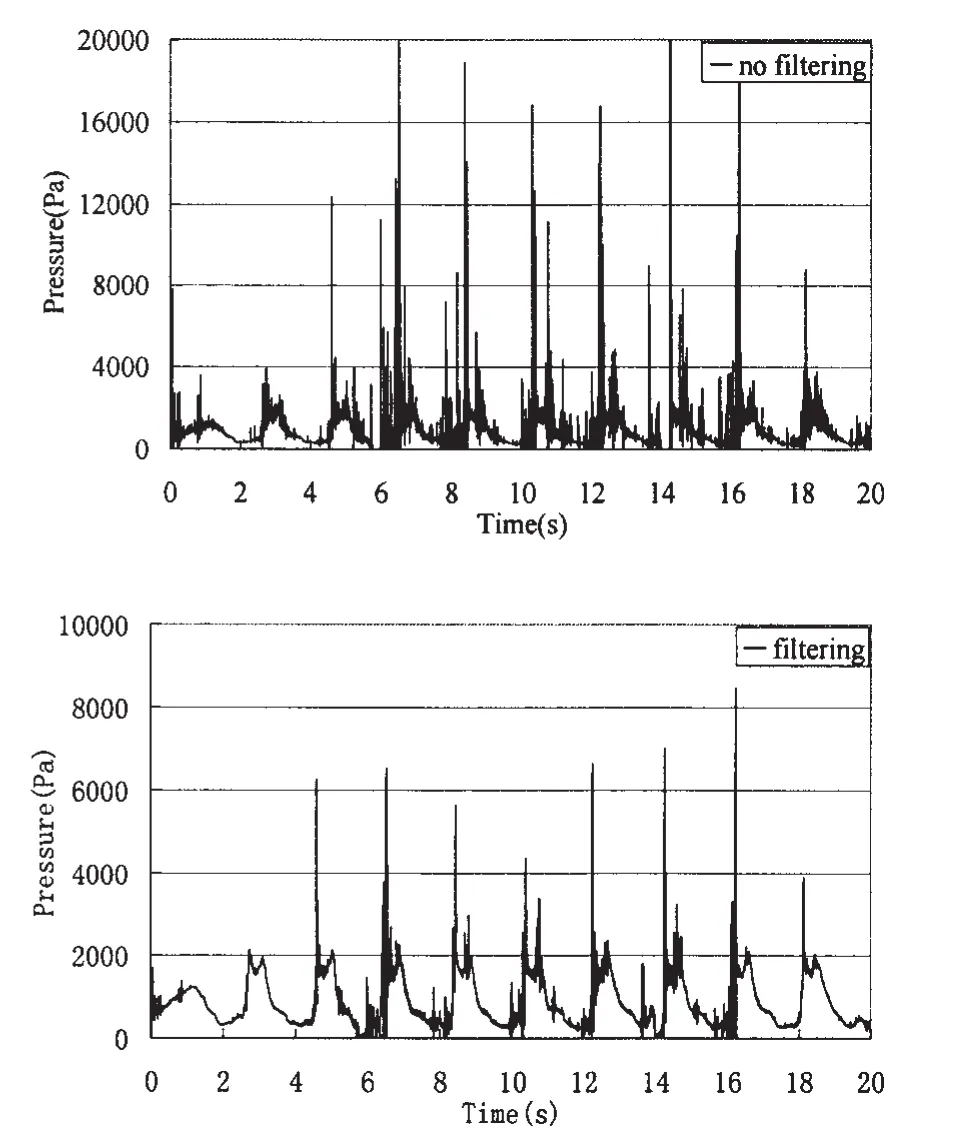
圖7 P2點的壓力時間歷程（20%H，K減縮）Fig.7 Time history of pressure P4(20%H,reduced K)

4 三維剛性及三維彈性矩形液艙模型

三維剛性模型同二維的相似，但在流體的非主要運動方向增設單元，放開流體僅在建模平面內運動的限制，使其可在非主要運動方向也能運動。實際LNG船液艙的圍護系統是由兩層絕熱聚酯材料組成的。因此，我們考慮的三維彈性模型（圖9）在三維剛性（圖8）模型的基礎上，在流體域與剛性壁之間加了一層采用Lagrange體單元劃分的結構域模擬夾層泡沫，引用DMATEP卡片定義各向同性線彈性材料來模擬此層彈性結構，參數設置依據真實的LNG船絕熱泡沫層物理量，體積模量K＝43.75 MPa，彈性模量E＝84 MPa。圖10和圖11是發生沖擊時液面圖。

圖8 三維剛性模型Fig.8 3D rigid model

圖9 三維彈性模型Fig.9 3D elastic model

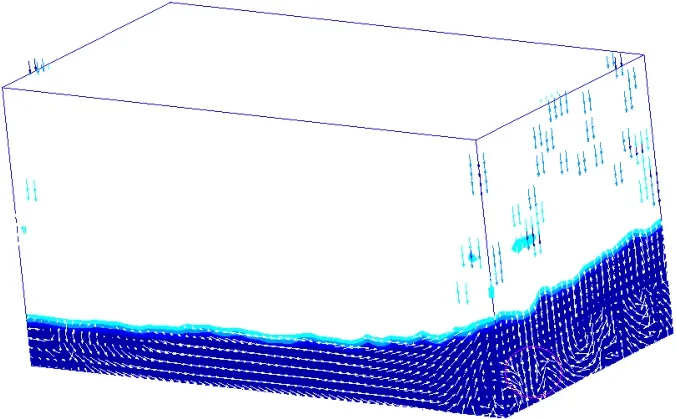
圖10 14.3 s時刻自由液面及流體速度矢量圖（20%H）Fig.10 Free surface and fluid velocity vectors at 14.3 s

圖11 14.6 s時刻自由液面及流體速度矢量圖（20%H）Fig.11 Free surface and fluid velocity vectors at 14.6 s

5 壁面彈性對晃蕩沖擊壓力的影響分析

由于是三維模型，我們取與測點同樣水平高度的相鄰三單元做空間平均得到該處的壓力，通過剛性和彈性結構模型處理計算得到的20%H裝載時液面附近P2點（圖12）和P3點（圖13）的壓力時間歷程，圖中我們可以觀察到壓力作用于彈性壁面的時間比剛性壁面的長，這是由于彈性響應形變的原因。

圖12 P2點的壓力時間歷程（20%H）Fig.12 Time history of pressure P2(20%H)

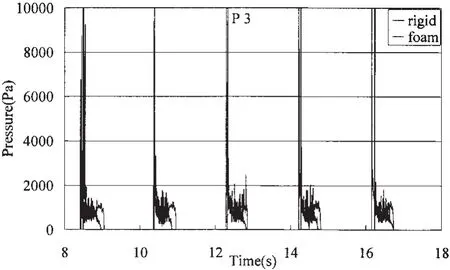
圖13 P3點的壓力時間歷程（20%H）Fig.13 Time history of pressure P3(20%H)

60%H裝載水平下泡沫材料的動能時歷（圖14）反應出彈性結構在給定的簡諧激勵下做簡諧運動；同時通過泡沫材料的變形能時歷（圖15）我們可以看出彈性結構在沖擊力作用下還發生了形變及反彈，開始未發生沖擊時變形平緩，而到沖擊力作用時刻變形能值遠高于其它時間；并且彈性結構自身也存在反復振動。

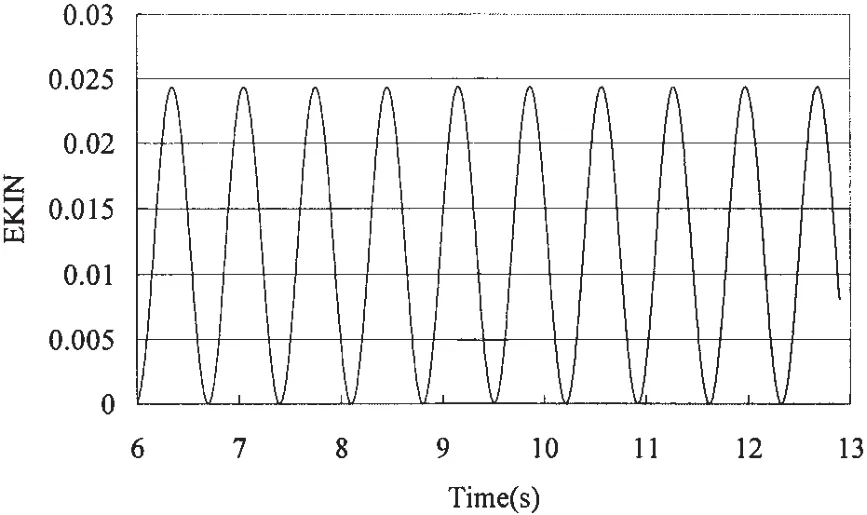
圖14 泡沫材料的動能時間歷程（60%H）Fig.14 Time history of kinetic energy of foam(60%H)

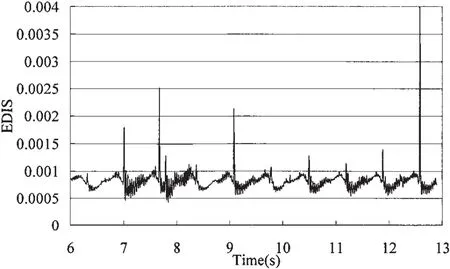
圖15 泡沫材料的變形能時間歷程（60%H）Fig.15 Time history of deformation energy of foam(60%H)

局部結構P6點處的大應變發生時間與結構大變形能（圖15）時刻基本一致，說明整體結構中該處的變形相對比較大，對變形能貢獻相對也最大；且應變（圖16）主要沿X方向，即垂直于艙壁板格的方向也是晃蕩沖擊時刻流體相對艙壁板格運動方向，其它方向的應變相對較小。對應的等效應力成分中（圖17），X方向的應力占主要地位，其它方向應力相對較小，剪切應力與他們相比更小，放在同一幅圖中幾乎可以忽略。

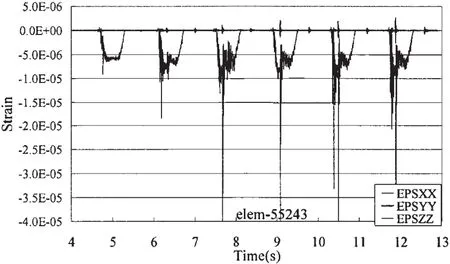
圖16 P6點處單元應變時間歷程（60%H）Fig.16 Time history of strain in element 55243 at P6(60%H)

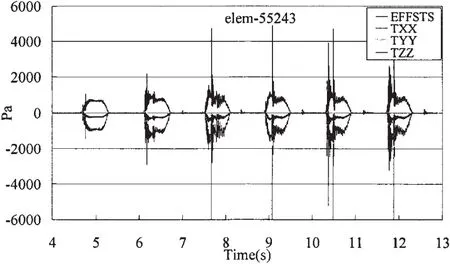
圖17 P6點處單元應力時間歷程（60%H）Fig.17 Time history of stress in element 55243 at P6(60%H)

圖18中是20%H裝載水平下P2和P3測點和60%H裝載水平下P4和P6測點的壓力統計值，液面下P2和P4點差異不大，而液面上的P3和P6點彈性模型計算值小于同工況下剛性模型計算值。

6 結 論

本文建立了基于顯式時間積分方法的有限元/有限體積法的流固耦合數值模擬技術，基于動力學仿真軟件DYTRAN對液艙晃蕩數值模擬方法進行了研究，并與CFD計算結果及試驗結果進行了對比分析。比較結果表明，本文提出的液艙晃蕩數值模擬方法是可行的。在此基礎上，進一步對大型LNG船液艙圍護系統的彈性壁面帶來的流固耦合問題開展了初步研究，發現艙壁彈性對晃蕩壓力幅值和持續時間有一定影響，需要引起研究和設計者的重視。

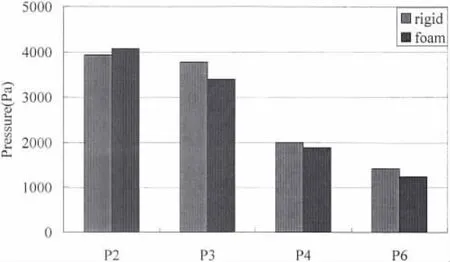
圖18 剛性模型和彈性模型各測點的壓力均值Fig.18 Mean pressures at different measuring points in rigid and elastic models

[1]Bergheim P,Thiagarajan K P.The air-water sloshing problem:Parametric studies on excitation magnitude and frequency[C]//Proceedings of 27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril,Portugal,2008.

[2]朱仁慶.液體晃蕩及其與結構的相互作用[D].無錫:中國船舶科學研究中心,2002.

[3]Zhu Renqing,Fang Zhiyong,Wu Yousheng.Numerical simulation of viscous liquid sloshing coupled with elastic structures[J].Journal of Ship Mechanics,2006,10(3):61-70.

[4]娜日薩.VLCC液艙晃蕩仿真及其結構強度評估方法研究[D].哈爾濱:哈爾濱工程大學,2006.

[5]Rognebakke O,Faltinsen O M.Hydroelastic sloshing induced impact with entrapped air[J].Hydroelasticity in Marine Technology,2006,1:169-180.

[6]Wang B,Kim J W.Strength evaluation of LNG containment system considering fluid-structure interaction under sloshing impact pressure[C]//Proceedings of 26th International Conference on Offshore Mechanics and Arctic Engineering.San Diego,California,USA,2007.

[7]Hisashi lto.A direct assessment approach for structural strength evaluation of cargo containment system under sloshing inside LNGC tanks based on fluid structure interaction[C]//Proceedings of 27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril,Portugal,2008.

[8]邢景棠,周 盛,崔爾杰.流固耦合力學概述[J].力學進展,1997,27(1):19-38.

[9]徐國徽,顧學康.液艙晃蕩砰擊壓力的數值計算方法研究[C]//第二十二屆全國水動力學研討會暨第九屆全國水動力學學術會議.成都,2009.

[10]Hughes T J R,Liu W K,Thomas K Z.Lagrangian-Eulerian finite element formulation for incompressible viscous flows[J].Computer Methods in Applied Mechanics and Engineering,1981,29:329-349.

[11]Donea J,Giuliani S.An arbitrary Lagrangian-Eulerian finite element method for trainsient dynamic fluid-structure interaction[J].Computer Methods in Applied Mechanics and Engineering,1982,33:689-723.

[12]Huerta A,Liu W K.Viscous flow with large free surface motion[J].Computer Methods in Applied Mechanics and Engineering,1988,69(3):277-324.