負壓波衰減系數及普通彎管泄漏檢測研究＊

陽子軒 范世東 江 攀 熊 庭

（武漢理工大學能源與動力工程學院1） 武漢 430063） （中國人民解放軍96212部隊2） 揭陽 515347）

0 引 言

隨著國民經濟的迅速發展，管道運輸在經濟發展中的角色越來越重要，但隨著管線的增多及設備運行時間的增長，管壁由于施工缺陷、沖刷腐蝕及人為破壞等原因，管線泄漏事故頻頻發生.對于管道泄漏檢測，目前國內外學者側重研究的是單根長輸管道泄漏檢測，而對于城市供水管網、船舶管道等帶有不少彎管的復雜管道泄漏檢測少有研究，開展對這類復雜管道的泄漏檢測研究同樣意義重大.

在對彎管進行研究時，由于流體在彎頭處會出現水力摩阻系數、流態等表述流體特征的物理量不一樣，從而造成負壓波衰減系數的不同.同時在泄漏計算過程中，對于彎頭處的當量長度換算也沒有計算公式.本文擬從實驗出發，對泄漏發生后的普通彎管的負壓波衰減系數及彎頭當量長度進行研究.

1 研究基礎

文獻［1］指出，90°彎頭的當量長度應根據HG／T 20570.7－95［2］管道壓力降計算標準計算，90°彎頭（標準型）的當量長度計算公式為

式中：Le為90°彎頭折算后的當量長度，m；D為管道內直徑，m.

但是HG／T 20570.7－95管道壓力降標準針對的是管道內流體經過90°彎頭時的局部阻力壓力降，而不是負壓波經過彎頭時的當量長度計算標準，因而這種方法是存在一定誤差的.

本文采用實驗的方法對彎頭當量長度進行研究.先根據測得的實驗數據計算出負壓波在普通直管中的能量衰減系數，然后根據實驗得到負壓波經過彎管時的衰減規律，方案見圖1.

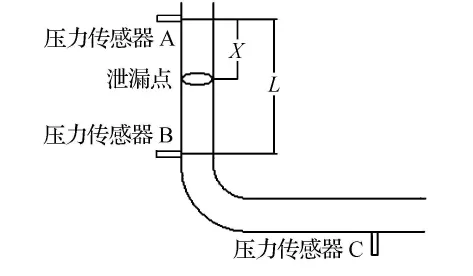
圖1 負壓波衰減系數確定方案圖

在能量傳播過程中，其傳播規律為p＝pine－αx.如圖1所示，當距離入口x點處發生泄漏時，依據上述規律［3］，則有

式中：px為泄漏點處的負壓波壓力值，Pa；pA，pB為A，B點負壓波壓力值，Pa；x為泄漏點距首端傳感器的距離，m；L為2個壓力傳感器之間的距離，m；α為負壓波衰減系數.

1）負壓波衰減系數的確定 實驗時，先進行管道運行的穩態實驗，得到A，B點的穩態運行壓力值，然后進行泄漏實驗，得到A，B點的泄漏時壓力值，二者的差值就是負壓波壓力值pA，pB.這樣在式（2）和（3）中，只有px和α2個未知數，解這2個方程，就可以得到泄漏點處的負壓波壓力值px和負壓波衰減系數α.

2）彎管當量長度的確定 在C處再安裝一個壓力傳感器，進行彎管泄漏實驗.由于負壓波衰減系數α已經得出，因而通過式（2）就可以算出泄漏點處的負壓波壓力值，將此值代入式（3），就可得到從B到C點的當量長度，然后減去B點到彎頭和彎頭到C點的距離，就可以得到彎頭的當量長度.

2 實驗方案及數據處理

2.1 實驗方案

為了研究負壓波在管道中傳播時的衰減規律，本文分3部分內容研究：（1）不同的泄漏量對負壓波衰減系數的影響；（2）不同的泄漏點對負壓波衰減系數的影響；（3）不同的首端壓力不同泄漏點對負壓波衰減系數的影響.為實現上述功能，在管道中選取了如圖2所示一段管道進行實驗.其中傳感器1對應于圖1中的壓力傳感器A，傳感器2對應于圖1中的壓力傳感器B，傳感器3對應于圖1中的壓力傳感器C.在圖2中，漏點3為電動調節閥，可以調節泄漏量大小，因而可以進行第一部分的研究內容；管道上布置了9個漏點方便進行第二部分的研究內容；實驗臺設計的8個泵［4］能保證第三部分研究內容的進行.

圖2 負壓波衰減系數研究所取管道布置圖（單位：cm）

需要指出的是，在管道施工時，漏點1～2、漏點5～9都是3mm的孔；漏點3作為電動調節閥是8mm的孔，在實驗中，不能精確的調到3mm孔泄漏量大小；漏點4是5mm的孔，綜合以上幾個因素，第二部分和第三部分的研究內容都只能有7個泄漏孔的數據較為合理.

在實驗臺上，除了漏點3是電動調節閥，其余漏點都是手動球閥.

2.2 實驗數據處理

1）壓力數據的采集 如前所述，在傳感器1和傳感器2的位置分別安裝一個壓力傳感器測量流體壓力，其型號為JYB－K0－HAG，輸出信號為4～20mA的電流信號.由于數據采集卡PCI－1710HG是電壓信號輸入，因此需要在數據采集卡的模擬輸入端并聯一個250Ω的精密電阻，將4～20mA的電流信號轉換為1～5V的電壓信號，這樣就可以通過數據采集卡輸入電壓的大小來確定壓力的大小.

2）壓力數據處理 在壓力測量過程中，測量系統得到的瞬時壓力服從正態分布，而且所有數據都是在等精度重復測量過程中獲得的.含有粗大的測量數據屬于異常值，應予以剔除.剔除數據常用的2個判定準則是：拉依達準則和格羅布斯準則［5］.

記錄某一工況下的穩態壓力時，每次對工控機讀到的數據采集卡上的數據記錄25個，剔除粗大誤差，然后求平均值，以這個值作為穩態的壓力值.

對于拉依達準則，由于標準誤差在評價正態分布的隨機誤差時具有特殊的意義，又因為理論計算表明，介于（±3σ）之間的隨機誤差出現的概率為

即測量數據呈正態分布，誤差大于3σ的概率僅為0.0027，如果測量次數為有限次，測量誤差（通常用殘差代替）大于3σ即可判定該測量數據含有粗大誤差，應予以剔除.該準則簡單實用，但不適合于測量次數≤10次的情況，可以證明，當n≤10時，殘差總是小于3σ的.

應該指出的是，剔除粗大誤差每次只能剔除一個數據，剔除數據后，應重新計算出測量數據的平均值和標準偏差，再按上述程序檢驗，直到粗大誤差全部剔除為止.

3 負壓波衰減系數研究

3.1 不同泄漏量對負壓波衰減系數的影響

不同泄漏量對負壓波衰減系數的影響研究按圖2所示的管道布置進行實驗，在圖2中，漏點3是電動調節閥，其開度可以從0%調到100%，方便本實驗的開展.在本文中進行了開啟2個泵時的10個不同工況泄漏開度實驗，分別為泄漏量的5%，10%，15%，20%，25%，30%，35%，40%，45%，50%，不同泄漏量工況下得到的數據及數據處理結果，得到不同泄漏量工況時的負壓波衰減系數變化趨勢如圖3所示.

圖3 負壓波衰減系數隨泄漏量大小變化規律圖

由圖3可見，當管道泄漏量較小時，負壓波衰減系數較大，隨著泄漏量越來越大，負壓波衰減系數趨于平穩，這和實際情況也是一樣的.泄漏量較小時，負壓波衰減較快，當負壓波傳播了一定距離以后，由負壓波引起的壓力變化量已經很小了，從而會影響到壓力的測量和突變點的檢測，這一狀況在小泄漏的誤檢上體現的特別明顯.隨著泄漏量增大，負壓波衰減慢慢趨于平穩，隨著泄漏距離的增加，負壓波衰減呈指數規律，壓力傳感器能測到壓力突變.因而從圖3可以得出一個結論：對于本實驗臺8mm孔徑處的泄漏，大于30%以上的泄漏量都能很好的檢測，而小于30%的泄漏量檢測屬于小泄漏檢測，也就是負壓波檢測的敏感點.

3.2 同一首端壓力不同泄漏點對負壓波衰減系數的影響

不同泄漏點對負壓波衰減系數的影響研究按圖2所示的管道布置進行實驗，在圖2中，由于漏點3是帶電動調節閥的8mm泄漏孔，控制泄漏量不太方便，漏點4是5mm的泄漏孔，而其他泄漏孔都是3mm的泄漏孔，因而實驗只在這7個3 mm的泄漏孔中間進行.開啟2個泵不同泄漏點的各種工況下得到的數據及數據處理結果，得到不同泄漏點工況下的負壓波衰減系數變化趨勢如圖4所示.

圖4 負壓波衰減系數隨泄漏點位置變化規律圖

從圖4可以看出，當泄漏點距離首端壓力傳感器較近時，負壓波衰減系數比較穩定，泄漏點越靠近尾端壓力傳感器，負壓波衰減系數越大，這與實際情況也基本是一致的.從圖2的漏點布局圖可以看出，泄漏點接近首端壓力傳感器的位置是直管道，水流較為穩定，因而負壓波傳播也比較穩定，負壓波衰減系數也相對穩定，泄漏點靠近尾端壓力傳感器時，特別是漏點9離2個90°的彎頭只相隔23cm，水流受阻使負壓波傳播也受到影響，進而引起負壓波衰減系數變大.因而從圖4可以得出結論：分析負壓波在直管中的傳播規律，可以用距離首端壓力傳感器387cm以內的數據，分析負壓波在彎管中的傳播規律，則用距離首端壓力傳感器510cm以后的數據.

3.3 不同首端壓力不同泄漏點對負壓波衰減系數的影響

不同首端壓力不同泄漏點對負壓波衰減系數的影響研究按圖2所示的管道布置進行實驗，按照3.2的方法進行實驗，開啟1個泵后，在不同泄漏點的各種工況下對數據進行處理，得到數據處理結果，從而不同首端壓力不同泄漏點工況下的負壓波衰減系數變化對比如圖5所示.

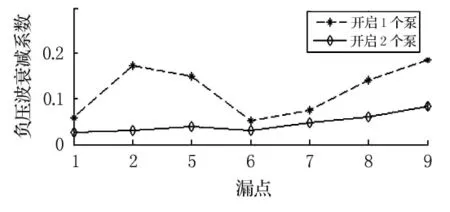
圖5 首端壓力不同時負壓波衰減系數對比圖

從圖5可以看出，開啟一個泵進行管道泄漏檢測實驗時，負壓波衰減系數沒有太多的規律，這是由于管道布局太為復雜，垂直落差、90°彎頭太多造成的.當首端壓力較低時，管道內水流極其不穩定，而且水流也沒有充滿整個管道，造成了測量誤差.因而從圖5可以得出一個結論：在本文設計的實驗臺中，進行管道泄漏檢測實驗效果最好的情況是開啟2個泵.

4 彎管當量長度確定

根據3.2的結論，研究負壓波在彎管中的傳播規律時，當泄漏孔越接近彎頭時，得到的結果越準確，因而本研究按圖2的管道布局上進行實驗時，壓力傳感器1，2，3上各安裝一個壓力傳感器，以漏點9作為研究對象，此時泄漏點相隔傳感器1距離為5.61m，相隔傳感器2距離為0.08m，傳感器2到傳感器3之間的直管距離為0.37m.

由圖2，從漏點到壓力傳感器3的距離為8＋15＋3＋11＝37cm，因而由2個90°彎頭產生的當量長度為（L－0.37）（m），在本文實驗臺中，由于2個90°彎頭相距很近，中間的直管長度只有3cm，從而可以近似的認為負壓波在這2個90°彎頭的傳播規律一樣，因而90°彎頭產生的當量長度為（L－0.37）／2，m.

根據實驗原理及實驗過程，對彎頭的當量長度數據進行曲線擬合，本文采用最小二乘法擬合，從而得到擬合曲線表達為

根據實驗數據和擬合曲線表達式，得到實驗數據及實驗數據擬合曲線見圖6.

圖6 當量長度計算數據及擬合曲線

從圖6可以看出，擬合后的最大誤差為12.1%，最小誤差為1.3%，雖然最大誤差稍微偏大，在這只是在數據處理過程產生的誤差.如果將這個誤差放入整個管道，那么由于數據處理而產生的誤差會小至（1.57－1.4）／5.98×100%＝2.8%.這個精度還是可以接受的.

綜合以上的分析結果，對于本文設計的實驗臺在進行彎頭當量長度換算時，可以近似的取最小二乘擬合后直線方程的截距（1.6m），從而在本文實驗臺中，90°彎頭（標準型）的當量長度計算公式為

式中：Le為90°彎頭折算后的當量長度，m；D為管道內直徑，D＝0.040m.

為檢驗此公式的合理性，將這一結果與文獻［1］附錄中的實驗結果進行對比.為了體現實驗條件的相似性，本文取文獻［1］附錄4穩態輸送時復雜管道泄漏檢測試驗結果中的部分數據，同時，因素B取第二個條件，對應于開啟2個泵，因素C也取第二個條件，對應于兩個90o彎頭的這一段管道.在文獻［1］中，和這兩個條件對應的實驗管道當量長度為L＝5.61＋0.08＋0.15＋0.03＋0.11＋2.4＝8.38m，而通過本文當量長度計算公式后，上式中的2.4m變成了3.2m，從而使本文實驗管道當量長度L＝8.38＋0.8＝9.18m.新的泄漏點定位距離首端壓力傳感器的距離與文獻［1］中定位距離關系為

式中：X′為采用本文當量長度計算公式后的定位距離，m；X為文獻［1］中的定位距離，m.

2個條件下，部分實驗結果的泄漏點定位見表1.

表1 采用新的當量長度計算公式后的定位結果對比

由表1可見，經過新的當量長度計算公式改進后，所有實驗的泄漏點定位精度都能得到提高.因而采用新的當量長度計算公式能減小由于不合理換算帶來的“軟”誤差，提高定位精度，從而證明新換算公式的合理性.

5 結 論

本文對帶90°彎頭的管道發生泄漏時進行研傳播規律究，基于本文的實驗臺，得出以下結論：

1）泄漏量小于30%的泄漏屬于小泄漏檢測，會給檢測與定位帶來難度.

2）研究彎頭處負壓波傳播規律時，泄漏孔最好靠近彎頭.

3）研究負壓波衰減系數時，一定要讓管道首端壓力足夠大，至少要讓流體充滿整個管道.

4）在進行管道彎頭處當量長度換算時，90°彎頭的換算公式為L＝40D.

［1］胡 瓊.在役管線泄漏檢測技術研究［D］.武漢：武漢理工大學，2009.

［2］中華人民共和國化學工業部.HG／T 20570－95管道壓力降計算［S］.北京：化工部工程建設標準編輯中心，1996.

［3］葛會平.長輸管線負壓波法最小可檢測泄漏量的研究與應用［D］.蘭州：蘭州理工大學，2009.

［4］HU Qiong，FAN Shidong.Pipeline leak detection testing system based on negative pressure wave and flow［J］.武漢理工大學學報：交通科學與工程版，2009，33（2）：402－406.

［5］陳花玲.機械工程測試技術［M］.北京：機械工業出版社，2002.