聲輻射阻抗傳感器的原理設計與標定方法研究＊

向 陽 郭志勇 王校清

（武漢理工大學能源與動力工程學院 武漢 430063）

有限元＋邊界元法是目前結構輻射噪聲預估中最常用的方法，但邊界元法存在奇異積分的處理，計算近邊界聲場時數(shù)值解很不穩(wěn)定乃至嚴重失真，波疊加法是改進這一問題的方法之一.用波疊加法求取結構輻射聲功率時，要用到結構的輻射阻抗矩陣，在安靜結構設計中常用附加點質(zhì)量的方法改變結構的輻射聲功率，其實質(zhì)就是改變了結構本身的輻射阻抗矩陣，由此可見結構的輻射阻抗矩陣在安靜結構設計中是十分重要的設計變量.結構的輻射阻抗矩陣可以通過解析法或數(shù)值計算的方法來求解，但這種方法對規(guī)則形狀的結構比較適合，而結構形狀復雜時，這種方法就不再適用.因此，本文研究用實驗法測定結構的聲輻射阻抗，實驗測定不受結構幾何形狀的制約，同時測定的聲阻抗在一定頻率范圍內(nèi)可具有較高的精度［1］，可作為解析法或數(shù)值法的補充方法，用于工程實踐中的安靜結構設計.

1 聲阻抗計算公式的導出

由波疊加法［2－3］可知，結構的輻射阻抗矩陣中任意一元素即任意2點間的聲阻抗Za，ik定義為

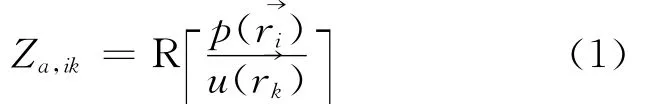
另外，實驗時用來模擬點聲源的揚聲器要用密封圈進行密封，保證其在工作時近似為一個點聲源.否則揚聲器的兩邊都將進行聲輻射，此時揚聲器更接近為一個偶極聲源，而不是一個點聲源，而偶極聲源在低頻時的輻射效率是很低的［4－5］.小聲源的平均輻射聲功率近似公式為

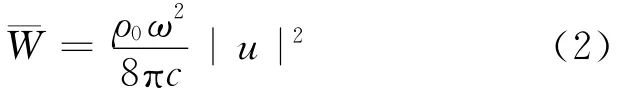
式中：ρ0為介質(zhì)的密度；c為聲速；ω為圓頻率（2πf）；u為聲源的體積速度.由式（2）可知，低頻時所輻射的能量較低.

由聲學理論可知，小體積腔室內(nèi)部聲壓大小取決于腔室內(nèi)做簡諧振動的壁面振速大小，用公式可表示為［6］

式中：u為腔室振動壁面的振動體積速度，見圖1a）；V為腔室的體積.

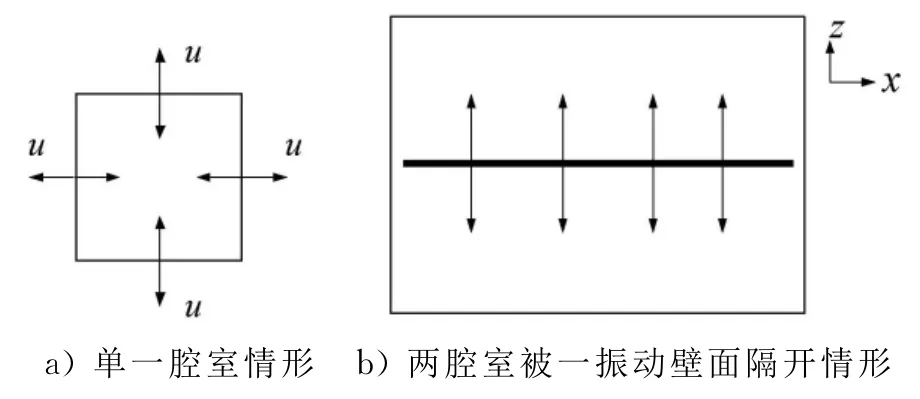
圖1 確定腔室內(nèi)聲壓示意圖

分析時忽略腔室內(nèi)駐波的影響，同時認為腔室的體積V為已知，且腔內(nèi)感知聲壓的麥克風沒有相位誤差，那么，通過測量揚聲器內(nèi)的聲壓就能用式（3）計算其振動體積速度.但是，實際使用的揚聲器的形狀是十分不規(guī)則的，其腔室的體積不易準確得到，此外，麥克風的相位誤差也是不能忽略的.因此，必須對聲阻抗測量裝置進行必要的校準，校準時需要在實驗用揚聲器上面設置一個已知體積的腔室（校準腔V2）.圖1b）為校準腔的示意圖，用式（3）可以得到2個腔室的聲壓比，即

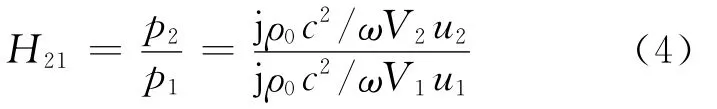
可以證明式（4）中體積速度u1和體積速度u2大小相等、方向相反.所以，式（4）可以化簡為

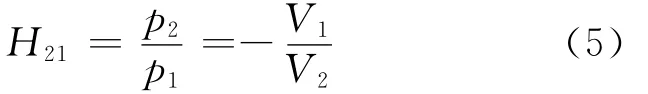
由式（5）可知，要想確定揚聲器腔室V1的體積，只需同時測量2個腔室內(nèi)的聲壓即可.

假設腔室2的直徑為d，沿x方向的長為l，且聲波以平面波的形式在其內(nèi)傳播，則根據(jù)式（6）可以計算得到沿腔室軸向上（z方向）的聲壓大小.

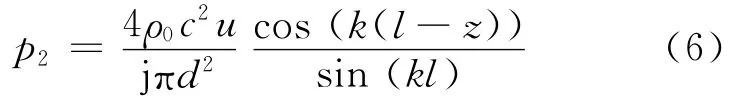
此時，只需測量腔室2頂部的聲壓（z＝l），腔室2的體積由V2＝πl(wèi)d2／4計算得到，則式（6）可以化簡為

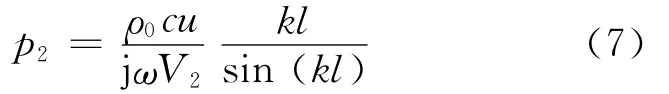
若用Vs和Vc分別代表聲源腔體積和校準腔的體積，ps為聲源腔內(nèi)的聲壓.由式（3）可得

將V1和V2分別用Vs和Vc代替后代入式（5），可得

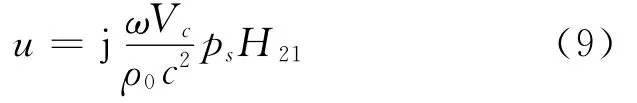
通過式（9）可以獲得結構表面任意一點k處的體積速度為

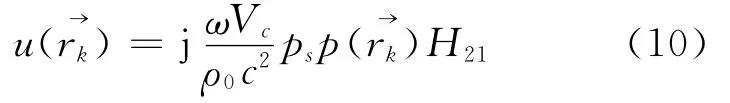
此時，只要再測量出結構表面任意一點i的聲壓，就可以由式（10）得到任意2點間的聲阻抗Za，ik

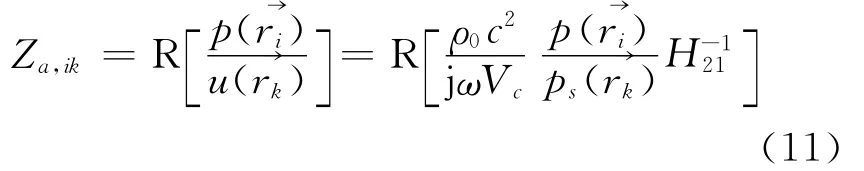
式中：i＝k時為自阻抗，i≠k時為互阻抗.

進一步化簡可得

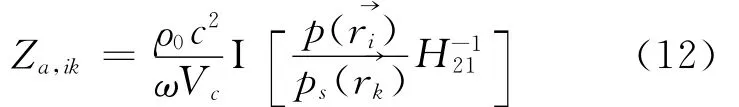
先通過校準實驗獲取H2－11就可以修正麥克風之間的相位不同，再通過所設計的測量裝置，逐點測量結構表面聲壓和聲源腔的聲壓就可用式（12）計算得到任意2點間的聲阻抗Rik.

2 校準腔的設計

根據(jù)上節(jié)所述校準原理，設計的校準腔見圖2.實驗時將圖2下部裝有揚聲器的聲源腔嵌入圖2上部的校準腔，揚聲器同時激勵校準腔和聲源腔，校準腔的聲壓由安裝在其頂部的麥克風測量，校準腔頂部安裝麥克風處和下部嵌入揚聲器處均需密封，校準腔的軸向長度l的設計準則是使其中的聲壓級變化不超過1dB.

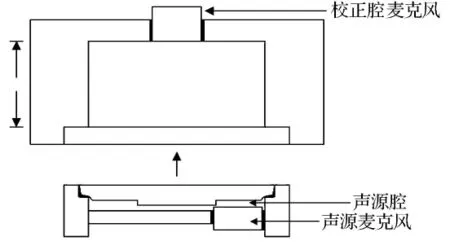
圖2 設計的校準腔示意圖

3 校準實驗

校準實驗系統(tǒng)見圖3.設備包括揚聲器1只、全指向性麥克風2只、NI9234采集模塊、NI9263電壓輸出模塊和cDAQ數(shù)據(jù)采集器，所選設備的性能指標見表1.

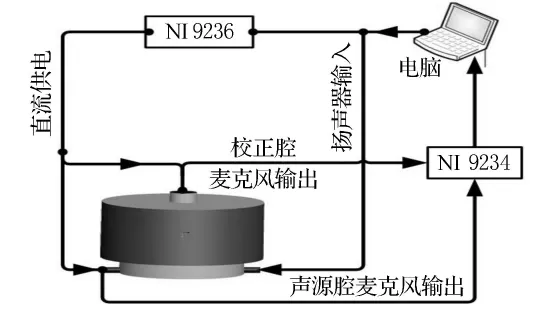
圖3 校準實驗系統(tǒng)圖

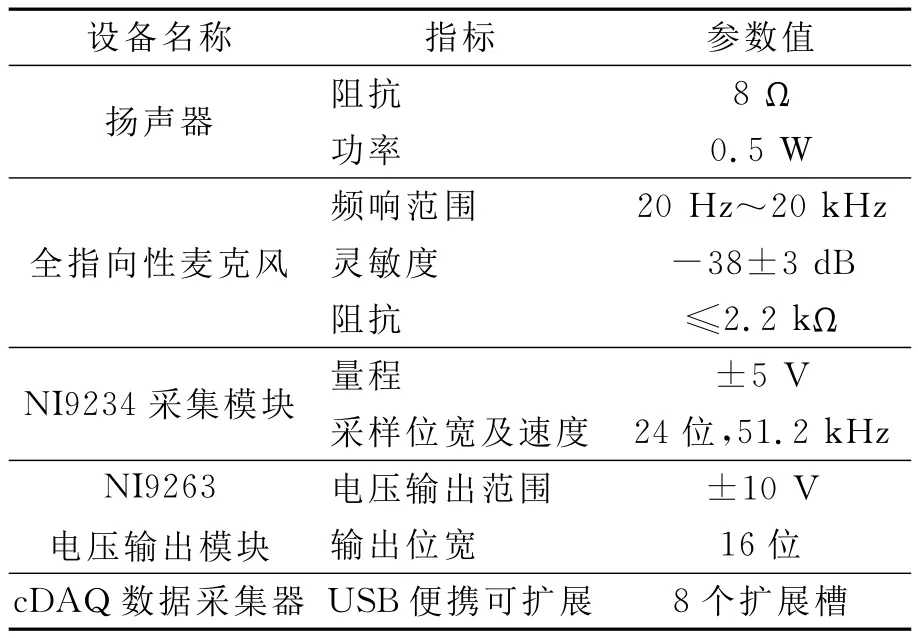
表1 主要設備性能參數(shù)

校準實驗在消聲室中進行，實驗裝置及測試系統(tǒng)見圖4.

圖4 校準實驗

實驗采用單頻正弦信號進行激勵，正弦信號的頻率范圍為200～3 100Hz，每間隔10Hz測量一次.將測量的數(shù)據(jù)進行信號處理后得到每個單頻點處H21的值，最后由這些單頻點處的H21值繪制其隨頻率變化的曲線.圖5～12為激勵頻率分別為600Hz和2 600Hz時，信號濾波前后的對比.

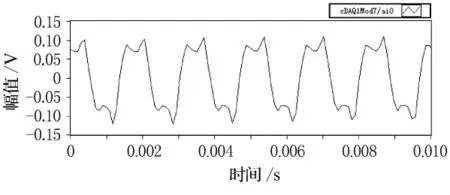
圖5 600時采集到的校正腔信號

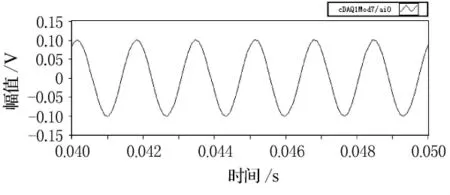
圖6 濾波后600Hz校正腔信號

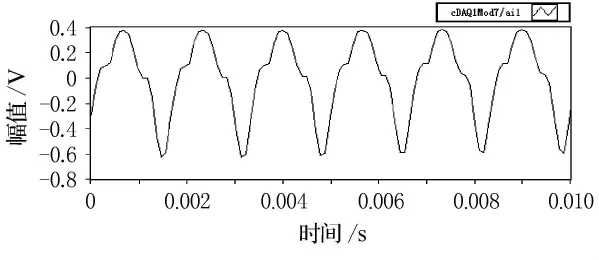
圖7 600Hz時采集到的聲源腔信號

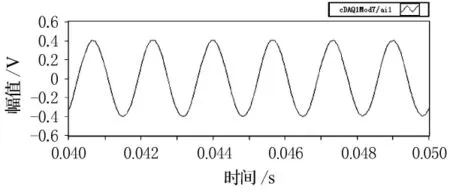
圖8 濾波后600Hz聲源腔信號

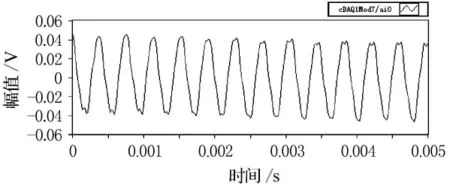
圖9 2 600Hz時采集到的校正腔信號

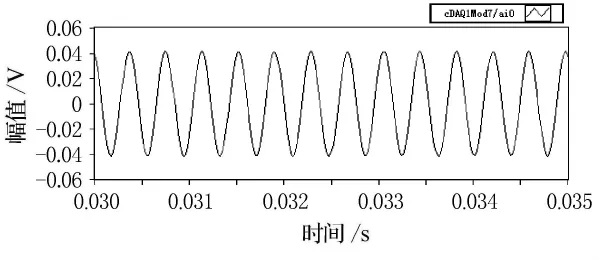
圖10 濾波后2 600Hz校正腔信號

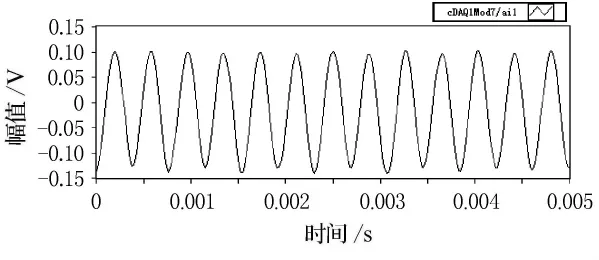
圖11 2 600Hz時采集到的聲源腔信號

由圖5～12的比較可以看出，揚聲器發(fā)出的單頻激勵在較低頻率時（600Hz），麥克風接收后產(chǎn)生較大的畸變，這主要是由于揚聲器在低頻時輻射聲波的能力不強造成的，但經(jīng)過濾波處理后，能較好的還原單頻正弦信號.隨著激勵頻率的逐漸升高（2 600Hz），麥克風采集的信號畸變也逐漸減小，濾波前后波形的形狀變化不大.

將所有采集的單頻信號數(shù)據(jù)都進行上面的濾波處理后，再通過加窗，F(xiàn)FT變換，最終可以得到每個采樣頻率點處的H21.圖13～16為1 600Hz處聲源腔和校準腔信號的頻譜實部、虛部，對比圖13和圖14以及對比圖15和圖16能夠發(fā)現(xiàn)，校正腔和聲源腔信號的相位正好相反，這與第一節(jié)中分析結論一致.圖17為最終所得的標定曲線H21.

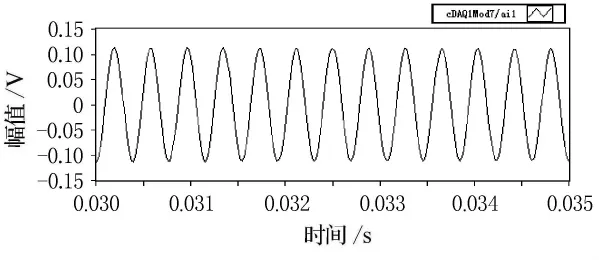
圖12 濾波后2 600Hz聲源腔信號

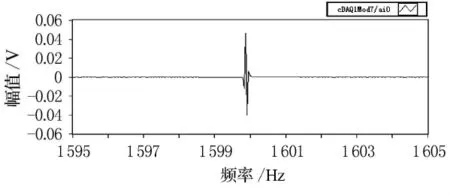
圖13 校正腔信號頻譜實部

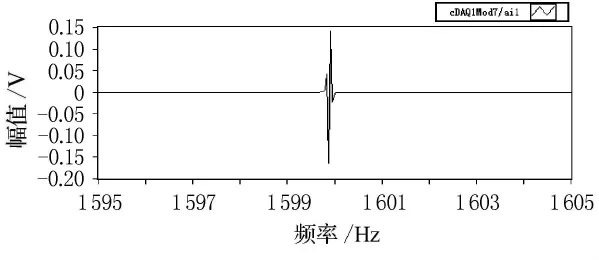
圖14 點聲源腔信號頻譜實部

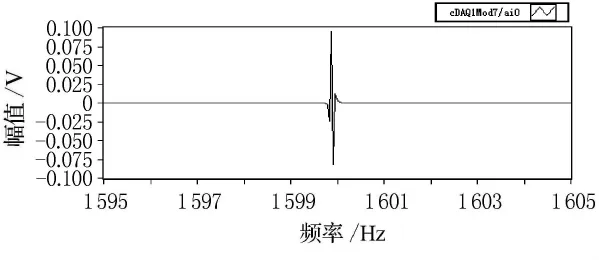
圖15 校正腔信號頻譜虛部

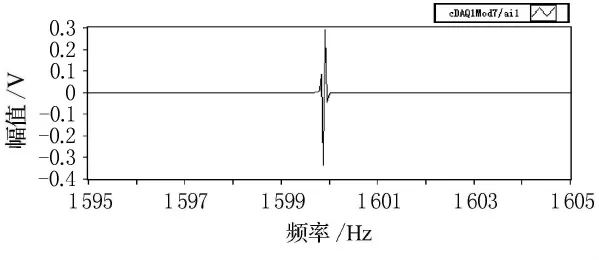
圖16 點聲源腔信號頻譜虛部

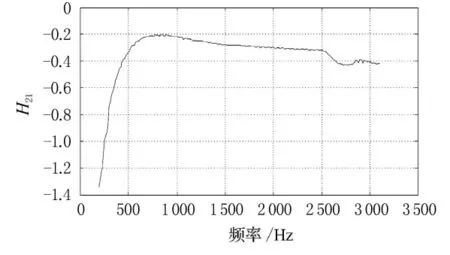
圖17 實驗得到的H21曲線

由圖17可以看出，在實際測量中2麥克風之間的相位關系并非固定不變，而是隨頻率變化而變化的.在低頻段兩麥克風之間的相位隨頻率變化較大；在中間頻段時兩者的關系較為穩(wěn)定；在高頻時兩者的關系也有一些波動，但變化不是十分劇烈.

4 結束語

研究了實驗測定聲阻抗的理論計算公式，然后根據(jù)聲學理論設計出實驗用的點聲源腔和校正腔，選取了合適的揚聲器、麥克風、信號采集設備并搭建了實驗系統(tǒng).并根據(jù)標定實驗所獲得的數(shù)據(jù)，通過信號后處理，最終得出兩麥克風之間的相位－頻率關系曲線.該校準曲線在后續(xù)的聲阻抗測量實驗研究中，將代入式（12）中用于聲阻抗的實際計算.

［1］KOOPMANN G H，F(xiàn)AHNLINE J B.Designing quiet structures［M］.San Diego：Academic Press，1997.

［2］向 陽，GARY H，KOOPMANN G H.基于波疊加原理的輻射聲場的計算研究［J］.武漢理工大學學報：交通科學與工程版，2005，29（1）：1－4.

［3］向 陽，郭志勇.波疊加法在結構輻射聲功率計算中的應用［J］.應用聲學，2010，29（1）：48－52.

［4］JORGE P，ARENAS A.Analysis of the acoustic radiation resistance matrix and its applications to vibroacoustic problems［D］.Auburn：Auburn University，2001.

［5］馬大猷.現(xiàn)代聲學基礎［M］.北京：科學出版社，2004.

［6］BERANEK.Acoustics［M］.New York：Acoustical Society of America，1986.