危險品運輸的集中管理模型＊

彭姍姍 孫會君

（北京交通大學交通運輸學院 北京 100044）

0 引 言

在危險品運輸的研究中，主要考慮的兩大問題是風險分析和網絡優化，本文主要考慮網絡優化問題.國內外不少學者就危險品運輸的風險分析和路線優化進行了研究.風險分析方法有定量分析和定性分析2種，最常用的是“傳統風險”模型［1］.在路線優化方面，Erkut和 Gzara［2］針對政府指定危險品運輸網絡及運營商選擇路線問題建立雙層規劃模型，該模型考慮運輸成本與風險的權衡，以運輸成本為上層目標.Kara和Verter［3］建立了一個基于路徑的危險品運輸設計模型，在該模型中，政府關閉某些路段從而使網絡中的總風險最小.Kazantzi等［4］采用最小費用流網絡問題的思想來研究危險品運輸路線優化問題，以盡量減少運輸成本和降低風險為目標，在滿足需求的條件下尋求最優的運輸路線.魏航［5］研究了時變條件下單一運輸方式有宵禁的危險品運輸最短路問題，建立了時變條件下有到達時間約束、具有多個出發時間和有軟、硬宵禁限制的危險品運輸最短路模型.

在現實的危險品運輸過程中，如果政府不對運輸者進行管理，運輸者在選擇路徑時不會考慮系統的風險，而只考慮自身的出行時間最優，有可能造成風險過大，而政府一般要考慮社會風險，則有可能損失運輸者的利益.所以，危險品運輸中必須要有政府的管理，然而政府在集中管理時，不僅要從自身的利益出發最小化網絡總風險，也要從運輸者的角度出發約束網絡中的總出行時間在一定范圍之內，從而使得運輸者愿意接受政府的統一安排.本文就是基于這樣的思想而展開研究的，在定義危險品運輸風險時，采用“傳統風險”模型并以暴露人口作為事故所造成損失；在建立了路徑選擇模型時，以網絡總風險最小為目標函數，并約束網絡中的總出行時間.在建立路徑選擇模型之前，先定義危險品運輸風險.

1 風險定義

在危險品運輸風險分析研究中，大多數學者采用“傳統風險”（traditional risk）模型，他們認為危險品運輸風險等于事故發生的概率與事故所造成損失的乘積［6］.

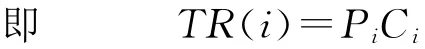
式中：TR（i）為危險品運輸風險；Pi為事故發生概率；Ci為事故所造成的損失.

首先，定義路段a發生危險品運輸事故的概率為

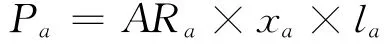
式中：ARa為路段a單位危險品車輛單位距離的事故概率；xa為路段a危險品車輛數；la為路段a長度.

根據“傳統風險”模型定義路段a的風險為

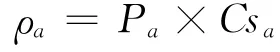
式中：Csa為路段a事故發生時的暴露人數，即路段a事故所造成的損失.

2 路徑選擇模型

危險品運輸的路線優化主要是研究如何降低運輸網絡中的風險，同時使運輸網絡的總費用最小.本文假設政府有權利安排每輛車的行駛路線，即政府集中管理網絡中的危險品車輛.在此假設的基礎之上，建立統一安排危險品車輛的系統最優模型.由于風險最小是政府考慮的目標，運輸車輛本身不會有這樣的目標，實現政府目標的危險品管理模式是集中管理模式，而只從運輸者角度考慮運輸時間（或距離等）最小的模式為分散管理模式.本文所建立的模型以風險最小為目標體現了政府的集中管理，為危險品運輸的集中管理模型.模型以網絡中的總風險（暴露人口）最小為目標函數，為了運輸者能接受政府的統一安排，運輸者的總出行時間不超過運輸者在無政府狀況下按UE（用戶均衡）原則選擇路徑時的總出行時間的θ倍.

基于此，建立的路徑選擇模型為

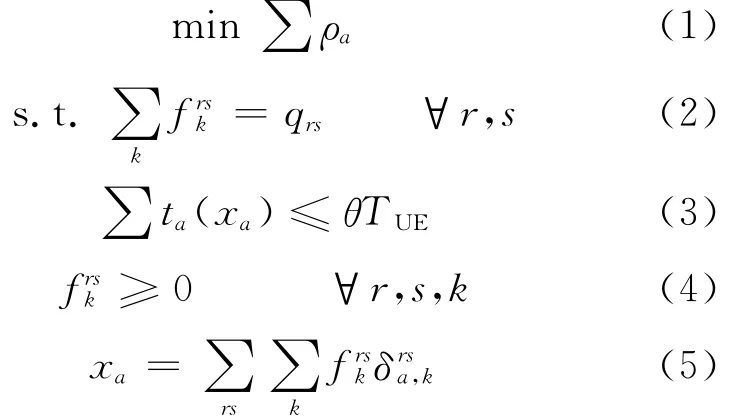
其中：式（1）為目標函數，即政府使網絡中的總風險（暴露人口）最小，式中：ρa為路段a的風險，由風險定義給出.式（2）為運輸網絡的需求約束，即OD對rs間所有路徑的流量之和等于rs間的總需求，其中frsk，qrs分別代表危險品車輛的路徑流量和需求；式（3）為政府從運輸者的角度考慮，使運輸者的總出行時間不超過運輸者在無政府狀況下按UE（用戶均衡）原則選擇路徑時的總出行時間（TUE）的θ（θ≥1）倍，從而使得運輸者能接受政府的統一安排，其中：xa為路段a危險品車輛數，ta（xa）采用BPR函數［7］形式，即ta＝t0a（1＋α（xa／Cij）β），t0a為路段a 的0流阻抗，α，β為回歸系數；式（4）為非負約束，即危險品車輛的路徑流量frsk應為非負；式（5）為運輸網絡中路段流量與路徑流量之間的關系式，如果路段a在OD對rs的第k條路徑上，則δrsa，k＝1，否則δrsa，k＝0.

3 算法設計

針對建立的危險品車輛流量分配模型，本文設計了相應的粒子群算法來進行求解.算法的思想是構造路線條數維的粒子空間，每一維對應一條可行性路線，其值為對應路線所分配的交通量，為使交通量守恒，應對粒子進行歸一化處理，并進行交通量的多路徑分配.根據目標函數評價與篩選粒子，直到滿足終止條件.參照基本粒子群算法［8］，設計求解本文模型的粒子群算法步驟為

步驟1 初始化.設置群規模m；最大速度V；最大迭代次數T；計算學習因子c1，c2；慣性權重 w 的參數c1f，c2f，c1i，c2i，w＿max，w＿min.并初始化粒子的位置和速度［9］.在此，粒子的位置向量yi取［0，qlrs］之間的隨機數，即表示路徑流量的取值為＝qrs×rand，為保證交通量守恒，需對其進行歸一化處理＝qrs／∑，每一維粒子的初始飛行速度取Vi＝V×rand.

步驟2 評價粒子.用目標函數評價每一個粒子的適用值.

步驟3 更新最優.（1）比較粒子的當前適用值與個體最優值pbest，如果優于個體最優值pbest，則將當前位置記為個體歷史最優位置pid；（2）比較粒子當前適用值與群體全體最優值gbest，若優于gbest，則群體最優位置pGd就是當前粒子位置；（3）根據群體最優位置pGd及式（3）計算得到xa.

步驟5 循環回到步驟2，直到達到最大迭代次數.

4 算例分析

如圖1所示，1為網絡的起點、6為終點.網絡中共有9條路段，取m＝80，T＝1 000，c1f＝c2i＝2.5，c1i＝c2f＝0.5，w＿max＝1.4，w＿min＝0.4，V＝4，α＝0.15，β＝4，qrs＝100pcu／min，其他參數見表1.

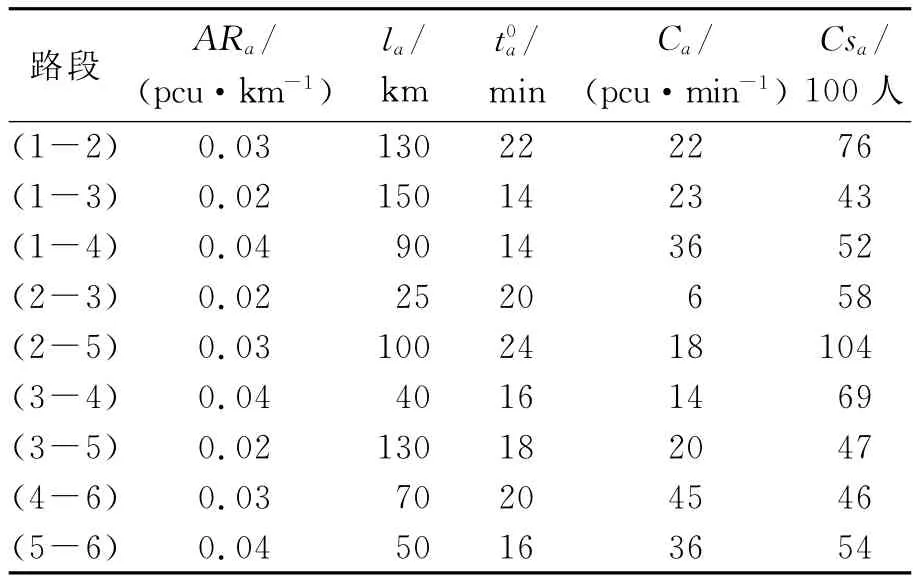
表1 算例參數

圖1 算例網絡圖

首先計算無政府狀態下網絡中的總出行時間，此時運輸者按UE（用戶均衡原則）進行路徑選擇，根據用戶平衡交通分配模型及F－W算法可計算得到，用戶均衡條件下網絡中的總出行時間為6 508.81min.

根據設計的粒子群算法，采用Matlab編程，得到網絡危險品總需求為θ＝1.5時的迭代收斂圖如圖2.由圖2可見，程序經過多次運行，算法在迭代20次后，目標函數值保持穩定，說明算法在迭代了20次后就開始收斂，所以本文采用的粒子群算法在計算所建立的模型上是收斂、有效的.

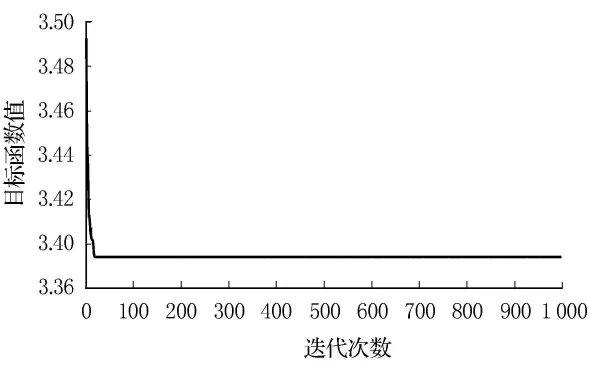
圖2 算法迭代收斂圖

約束式（3）中的θ表示了政府與運輸者之間的權衡，θ的大小反映出了政府考慮運輸者利益的程度.為了分析θ的取值對本文所考慮的危險品運輸問題的影響，本文在θ取不同值時的情況下對模型進行了求解.求解得到θ取不同值時的網絡總風險見表2.

表2 θ取不同值時的網絡總風險100人

在表2中，當θ≥4時，網絡總費用保持不變.為了更加直觀的反映表2的信息，將表2反映到折線圖中，見圖3.

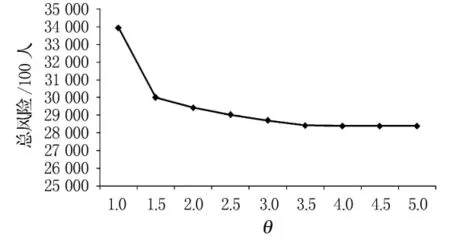
圖3 取不同值時的網絡總風險

由圖3可見，網絡的總風險隨著θ的取值不同而變化.當θ的取值為（1.0，4.0）時，網絡的總風險隨著θ的取值增大而減小，且隨著θ的增大，總費用減小的速度越來越小.最后當θ的取值超過4.0時，網絡總風險不再減小，此時θ對模型失去約束力，相當于不考慮約束式（3）的情形.

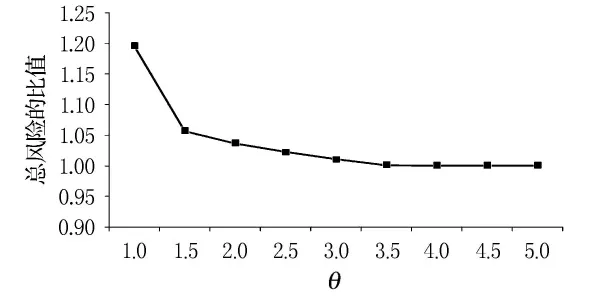
為了突出建立的考慮約束式（3）的路徑選擇模型較之于不考慮約束式（3）的路徑選擇模型的優越之處.θ取不同值時的總風險與最小總風險（不考慮不考慮約束式（3）時的總風險）的比值見圖4.

由圖4可見，在θ的取值從1.0增加到1.5的過程中，總風險相對于最小總風險的比值從1.2減小到1.06，在θ的取值從1.5增加到4.0的過程中，總風險相對于最小總風險的比值卻僅從1.06減小到1.從而可以看出當θ的取值大于1.5時，總風險的減小速度是很慢的，從而導致運輸者總出行時間的較大幅度的增加，卻只能獲得較小幅度的總風險的減小.這對于社會總效率來說顯然是不可取的.所以政府在做決策時，取θ為1.5或略小于1.5的值是比較合適的，這樣既能有效的減小網絡的總風險，也能獲得政府與運輸者效益之間的一個權衡，既有利于政府，運輸者的利益損失也不太大.

5 結束語

在定義危險品路段風險的基礎上，建立了由政府集中管理情況的危險品運輸網絡優化模型，模型以網絡中的總風險最小為目標函數，并約束運輸者的總出行時間不超過運輸者在無政府狀況下按UE原則選擇路徑時的總出行時間的θ倍.針對一個簡單的算例分析了θ取不同值時網絡中的總風險的變化情況.在一定范圍內，網絡中的總風險隨著θ的增大而減小，且減小的速度越來越小，當θ超過一定值時網絡中的總風險不再變化.最后，針對算例分析了政府在做決策時的比較合適的θ取值.雖然這個算例不具有一般性，但是針對不同的實際情況，本文所建立的模型和采用的算法仍能為政府的決策提供有價值的參考方案.

［1］ERKUT E，VERTER V.Modeling of transport risk for hazardous materials［J］.Operations Research，1998，46（5）：625－642.

［2］ERKUT E，GZARA F.Solving the hazmat transport network design problem［J］.Computers ＆ Operations Research，2008，35：2234－2247.

［3］VERTER V，KARA B Y.A path－based approach for hazmat transport network design［J］.Management Science，2008，54（1）：29－40.

［4］KAZANTZI V，KAZANTZIS N，GEROGIANNIS V.Risk informed optimization of a hazardous material multi－periodic transportation model［J］.Journal of Loss Prevention in the Process Industries，2011（24）：767－773.

［5］魏 航.時變條件下有害物品運輸的路徑選擇研究［D］.成都：西南交通大學，2006.

［6］邵春福.交通規劃原理［M］.北京：中國鐵道出版社，2004.

［7］陳 玉.城市道路阻抗函數模型研究［D］.西安：長安大學，2008.

［8］李 丹.粒子群優化算法及其應用研究［D］.沈陽：東北大學，2006.

［9］陳 曦.粒子群優化算法的改進及在動態交通分配問題中的應用［D］.長沙：長沙理工大學，2006.