混合改進蟻群算法的函數優化

陳明杰，黃佰川，張旻

(哈爾濱工程大學自動化學院，黑龍江哈爾濱150001)

自2000年國際頂級學術刊物《Nature》發表了M.Dorigo的蟻群算法綜述以來，模擬自然界螞蟻進行最優路徑搜索的蟻群算法 (ant colony optimization，ACO)［1-13］作為求解組合優化問題的有效手段，逐漸成為智能優化算法領域的熱點［1］.由于其算法上具有正反饋機制、分布式計算、貪婪式搜索特征以及魯棒性強、并行處理等特點［2］，目前已被廣泛應用于組合優化問題中，在車輛調度問題、機器人路徑規劃問題等領域均取得了良好的效果.對一般函數的優化問題也表現出優異的性能，它可以克服傳統優化方法的許多不足和缺陷，實現簡單，在函數不連續、不可微、局部極值點密集等苛刻的情況，仍然具有很好的尋優能力［3］.W.J.Gutjahr發表的證明蟻群算法收斂性的文章在蟻群算法的發展過程中具有重要的意義［10］.但是，到目前為止，蟻群算法仍然存在很多不足，如易出現停滯現象、搜索時間長和解空間搜索不夠等缺點［4］.針對蟻群算法存在的上述問題，本文在文獻［5］的基礎上加以改進，提出了一種混合改進蟻群算法，并將其應用于函數優化問題中.

1 基于蟻群算法的函數優化原理

文獻［5］所提出的基于蟻群算法的函數優化原理如下.

不失一般性，在函數的優化問題中，所有的優化問題都可以表示為一個函數的最小化問題，即:

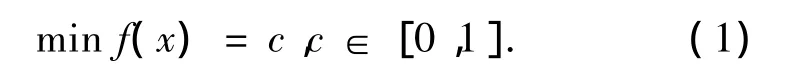
式中:c為常數.如果在函數優化中存在端點值，那么可以先將端點值剔除，最后計算比較.在下面的算法中將不再考慮端點值.

在多元函數優化問題中，設決策變量由n個分量組成，并要求決策變量的每一個分量都精確到小數點后d位，則可構造一副由n×d+n+1層數字組成，且第1、d+2、2d+3，…層由一個標號為0的數字組成，其余層都由標號為0～9的10個數字組成，第(b－1)×(d+1)+2到 b×(d+1)層(b=1，2，…，n)表示決策變量的第b個分量，其余層都是輔助層.解碼時，對各分量對應的層分別解碼.采用這種方法，每個決策變量分量的最后一位與下一個分量的第一位之間都有輔助層隔開，因此前一個分量的末位不會影響后面一個分量的首位.

將待優化函數的決策變量表示為一串十進制的數字串{d(0)，d(1)，…，d(l－1)}，而決策變量可以通過解碼公式(2)解碼得到［6］:

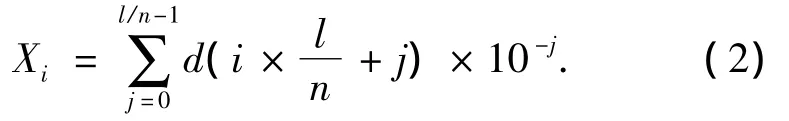
式中:l為決策變量字符串的長度，n為決策變量的維數.式(2)所代表的解碼過程可以用圖1來描述.

圖1 螞蟻路徑選擇Fig.1 Chosen path of ants

假設l=8，n=2，那么圖1所示的路徑由式(2)解碼后得到的決策變量為X=(X1，X2)=(0.206 4，0.971 3).

在圖1所示的螞蟻路徑選擇中，可知在螞蟻路徑的終點和起點之間有很多層數字.螞蟻要想從起點走到終點就必須經過每層數字，這樣螞蟻在每經過一層數字時，將會從10個數字中做出選擇，螞蟻在經過下層數字時從哪個節點經過根據式(3)選擇:

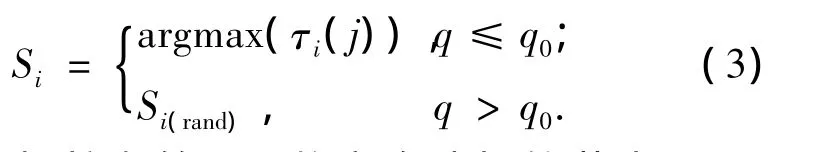
式中:Si為螞蟻在第i層數字會選擇的節點號碼;argmax為第i數字層上使得τi(j)最大的節點j的值;τi(j)是第i層數字上第j個節點上的信息素殘留量，q是一個隨機數，且 q∈［0，1］，q0是信息素閾值，q0∈［0，1］，根據經驗一般設為0.8;Si(rand)為第 i層數字中j號節點被螞蟻選中的概率，由式(4)計算得出:

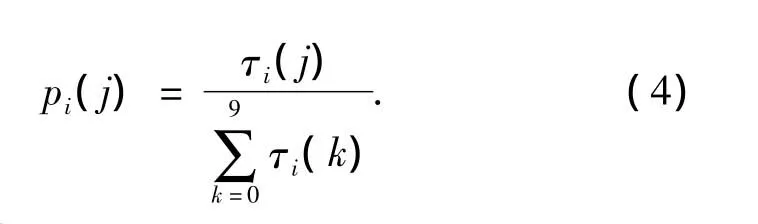
式中:pi(j)為第i層數字中節點j被螞蟻選擇的概率.

螞蟻每經過一層數字中的某個節點時，都會根據局部信息素殘留更新式(5)，修改該節點上的信息素殘留量.

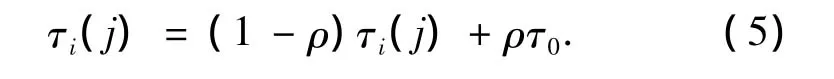
式中:τ0是常數，表示初始時刻信息素的含量;ρ是數字節點上的信息素揮發速度，ρ∈［0，1］.

當螞蟻如圖1所示在每層數字中選擇好一個節點后，這時螞蟻就找到了一條路徑.將這條路徑按式(2)解碼可以獲得決策變量的值，這樣就可以求得函數值.當蟻群中每只螞蟻都按照圖1找到一條路徑后，就可以在蟻群中找到一只螞蟻，它走過的路徑解碼后得到的決策變量使函數值最小，稱這只螞蟻為迭代最優螞蟻.讓迭代最優螞蟻的函數值和全局螞蟻的函數值相比較，如果迭代最優螞蟻路徑解碼后求出的函數值要小于全局最優螞蟻解碼后求出的函數值，那么迭代最優螞蟻成為全局最優螞蟻.當蟻群中每只螞蟻都選擇好路徑后，這時全局最優螞蟻要根據信息素殘留量的全局更新式(6)對所經過的第i層數字的第j個節點上的信息素殘留量τi(j)進行更新:

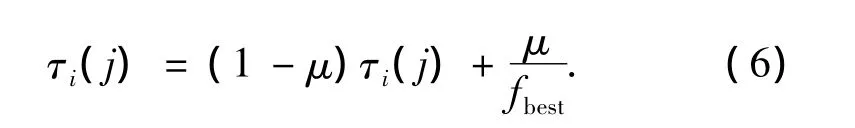
式中:τi(j)為最優螞蟻在第i層數字中所選擇的節點j上的信息素殘留量;μ是一個常數，且μ∈［0，1］;fbest表示全局最優螞蟻解碼后求出的函數值.

該蟻群算法就是一直重復進行上述螞蟻選擇的路徑和信息素更新的過程，至滿足結束條件.

文獻［5］所提到的蟻群優化算法采用十進制編碼，縮短了螞蟻需要搜索的路徑長度;信息素直接存儲在數字層的數字上面，減少了信息素的存儲量;采用了信息素局部更新和全局更新相結合的信息素更新規則.但上文所提到的蟻群優化算法仍然有不足:1)容易陷入局部最優，算法的全局搜索能力有待提高;2)在處理維數較多的函數問題時，搜索速度有待提高.

2 混合改進蟻群算法的原理

本文在文獻［5］的基礎上研究了一種基于自適應信息素揮發因子、決策變量高斯變異和決策變量邊界自調整3種改進策略的混合改進蟻群算法，提高基本蟻群算法的收斂速度和全局搜索能力.

2.1 基于自適應信息素揮發因子的蟻群算法改進

研究發現，蟻群算法是啟發式算法和信息素正反饋機制相結合產生的算法.在蟻群算法搜索最優解過程中，應用的是隨機選擇策略，而隨機策略會使蟻群算法的進化速度較慢;蟻群算法中的信息素正反饋機制的目的在于強化螞蟻搜索到的較優的解，但很容易出現停滯現象［7］.這正是蟻群算法的不足之處.

為了克服上述不足，在蟻群算法的尋優過程中，當迭代一定次數、進化方向基本確定時，利用自適應改變信息素揮發因子大小的方法，對尋優路徑上的信息素作動態調節，逐漸縮小最優路徑和最差路徑上的信息量，以實現對決策變量空間的充分尋優.

本文引入一種自適應信息素揮發因子，探討了一種基于自適應信息素揮發因子的蟻群算法的改進.該方法旨在使產生的新的蟻群算法通過信息素揮發因子μ的自適應來提高算法的全局性.即將式(6)中的全局信息素揮發因子μ用隨迭代自適應的μ(t)代替，此時式(6)變為

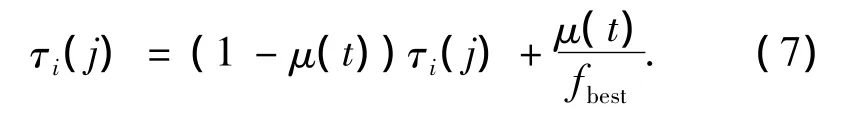
式中:μ(t)是隨迭代變化的信息素揮發因子，μ(t)按式(8)進行自適應變化:

式中:μmin表示 μ的最小值，其目的是可以防止由于μ過小使算法的收斂速度變慢.為了提高算法的全局搜索能力，提高算法的搜索速度，在每次循環搜索結束時，都求出最優解，并將最優解保留，作為判斷μ自適應的條件.

2.2 基于決策變量高斯變異的蟻群算法改進

在蟻群算法的搜索尋優過程中，當優化函數的非全局極值點比較集中時，會影響算法的收斂速度，并可能陷入局部最優，得不到高精度的解.為了使搜索到的解有更好的遍歷性，收斂速度更快，擺脫局部最優，本文加入決策變量高斯變異策略，將待優化函數的決策變量進行高斯變異，提出了一種基于決策變量高斯變異的蟻群改進算法.以加強解的多樣性，擴大搜索范圍，使算法在搜索過程中加快搜索速度，擺脫局部最優.

基于決策變量高斯變異的蟻群算法改進原理如下［8］.

高斯分布式概率論是數理統計中一類重要的分布.將高斯變異應用到蟻群算法，其思想主要來自于遺傳算法中的變異因子.在蟻群算法中應用高斯變異來改善蟻群算法的全局搜索能力，避免早熟，并加快收斂速度.式(9)是以原點為中心的高斯函數(Gaussian)，其概率分布如圖2所示.

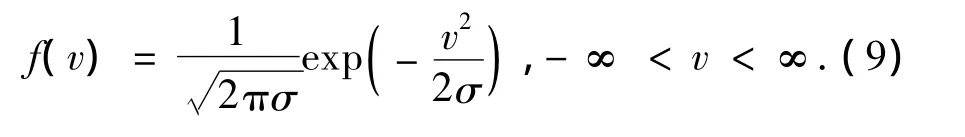
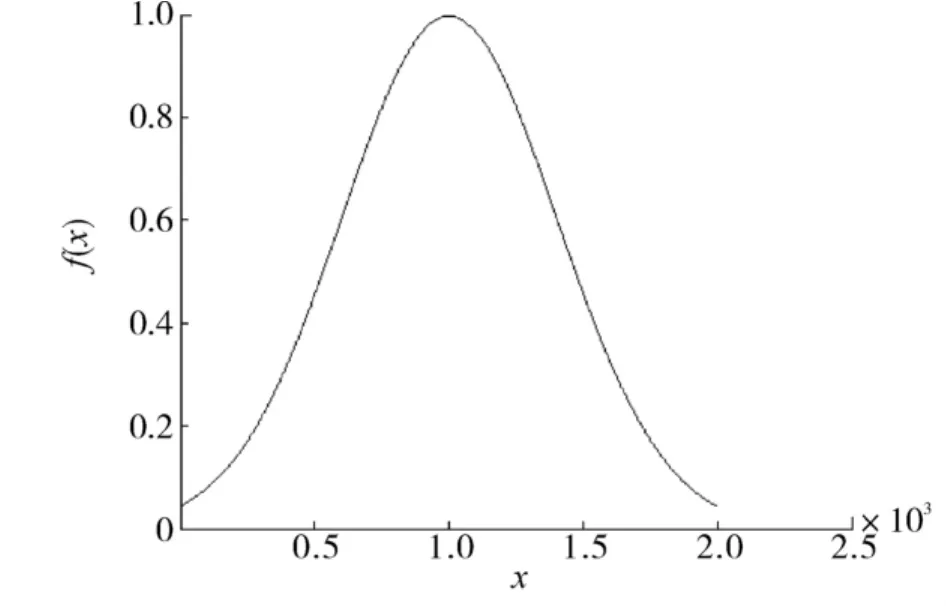
圖2 高斯分布概率分布Fig.2 Gaussian distribution

在式(1)所示的函數優化問題中，函數的決策變量用X表示，決策變量的維數為n;lb表示決策變量的下界，每一維決策變量的下界用lb(i)表示;ub表示決策變量的上界，每一維決策變量的上界用ub(i)表示;設MX表示經高斯變異后的決策變量，MX(i)表示變換后的第i維決策變量;為了使高斯分布覆蓋整個決策變量空間，設Gaussian分布函數中的參數σ =0.16.

決策變量高斯變異基本步驟如下:

1)給經高斯變異后的決策變量賦初值;

2)求出決策變量上下界的均值和均方差;

3)根據Gaussian分布函數產生一個均值為2)求出的決策變量上下界的均值，均方差為2)求出的決策變量上下界的均方差的隨機數;

4)將3)產生的隨機數限定在決策變量的上下界之間;

5)將4)產生的隨機數作為高斯變異后的決策變量.

2.3 基于決策變量邊界自調整的蟻群算法改進

在蟻群算法的尋優過程中，特別是在高維的函數尋優中，由于蟻群的尋優范圍較大，搜索的隨機性也很大，為了加快蟻群的搜索速度，克服算法陷入局部最優，本文引入決策變量的邊界自調整策略，研究了一種基于決策變量邊界自調整的蟻群算法改進方法.

決策變量的邊界自調整策略的原理主要是在算法的迭代尋優過程中，通過對決策變量邊界進行自調整，使算法的尋優范圍不斷向最小適應值附近收斂，以加快收斂速度，克服局部最優.

加入決策變量邊界自調整的改進蟻群算法步驟如下:

1)設定決策變量的上下界、決策變量維數、螞蟻個數.

2)初始化決策變量矩陣，即在決策變量的上下界之間隨機產生一個初始化矩陣.

3)開始進行循環，當未達到要求的迭代步數時，決策變量的邊界按式(10)、(11)進行自調整:

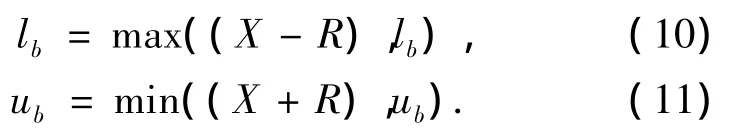
式中:R為一個在(0，1)上隨迭代變化的常數，用來控制決策變量的邊界.

在迭代尋優過程中，決策變量的邊界不斷按上述原理進行自調整，這樣在尋優的初期，蟻群會在整個決策變量定義域內尋優，搜索范圍較大，全局性較好;隨著尋優的進行，決策變量的范圍逐漸變小，向最優解附近收縮，這樣有助于提高算法的尋優速度.

2.4 混合改進蟻群算法

融合上述基于自適應信息素揮發因子、決策變量高斯變異以及決策變量邊界自調整3種策略，本文提出了一種混合改進蟻群算法.其程序流程圖如圖3所示.

混合改進蟻群算法的具體實現步驟如下:

1)初始化.設置螞蟻個數 m，最大循環次數Ncmax，初始化循環次數Nc和信息素含量.

2)將初始化蟻群放置在路徑選擇圖的初始點.

3)設置循環次數Nc=Nc+1.

4)對所有螞蟻進行4)～5).

5)選擇螞蟻在下一層到達的節點.此選擇按照式(3)、(4)進行.

6)在每只螞蟻選擇好下一層到達的節點后，按照式(5)進行局部信息素的更新.

7)當所有的螞蟻完成一次循環后，按式(8)更新μ，然后按照式(7)進行全局信息素更新.

8)根據式(10)和(11)進行決策變量邊界自調整，調整蟻群搜索范圍.

9)根據式(9)對決策變量進行高斯變異.

10)如果循環次數Nc≥Ncmax，即滿足結束條件，則循環結束并輸出程序計算結果;否則繼續.

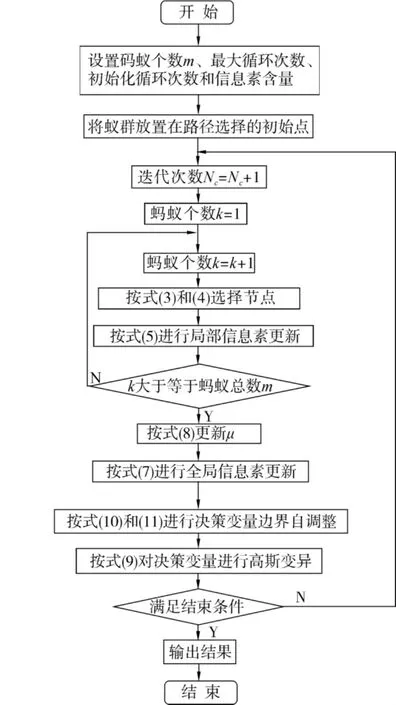
圖3 混合改進蟻群算法程序流程Fig.3 Flow chart of hybrid improved ACO

3 混合改進蟻群算法的仿真與分析

本文分別采用 Sphere、DeJongF4、Rosenbrock、Griewank和Rastrigin 5個基準測試函數作為適應度函數，分別應用文獻［5］中的基本蟻群算法以及基于信息素揮發因子自適應的蟻群算法、基于決策變量高斯變異和信息素揮發因子自適應的蟻群算法，和基于信息素揮發因子自適應、決策變量高斯變異、決策變量邊界自調整三者相融合的混合改進蟻群算法進行仿真實驗.其中，參數設置為:螞蟻個數為30，迭代次數為30，基準函數決策變量為五維，以最大迭代次數作為算法的終止條件，對5個基準函數各進行50次試驗.選取字節點上的信息素揮發速度ρ=0.3，Gaussian 分布函數中的參數 σ =0.16.則其仿真結果具體數據見表1和圖4～8所示.

表 1中，f1～f5分別代表 Sphere、DeJongF4、Rosenbrock、Griewank和Rastrigin 5個基準測試函數;基本蟻群是指文獻［5］的蟻群算法;改進蟻群算法1指基于自適應信息素揮發因子的改進蟻群算法;改進蟻群算法2指基于自適應信息素揮發因子和決策變量高斯變異策略的改進蟻群算法;改進蟻群算法3指基于自適應信息素揮發因子、決策變量高斯變異策略和決策變量邊界自調整策略的混合改進蟻群算法.

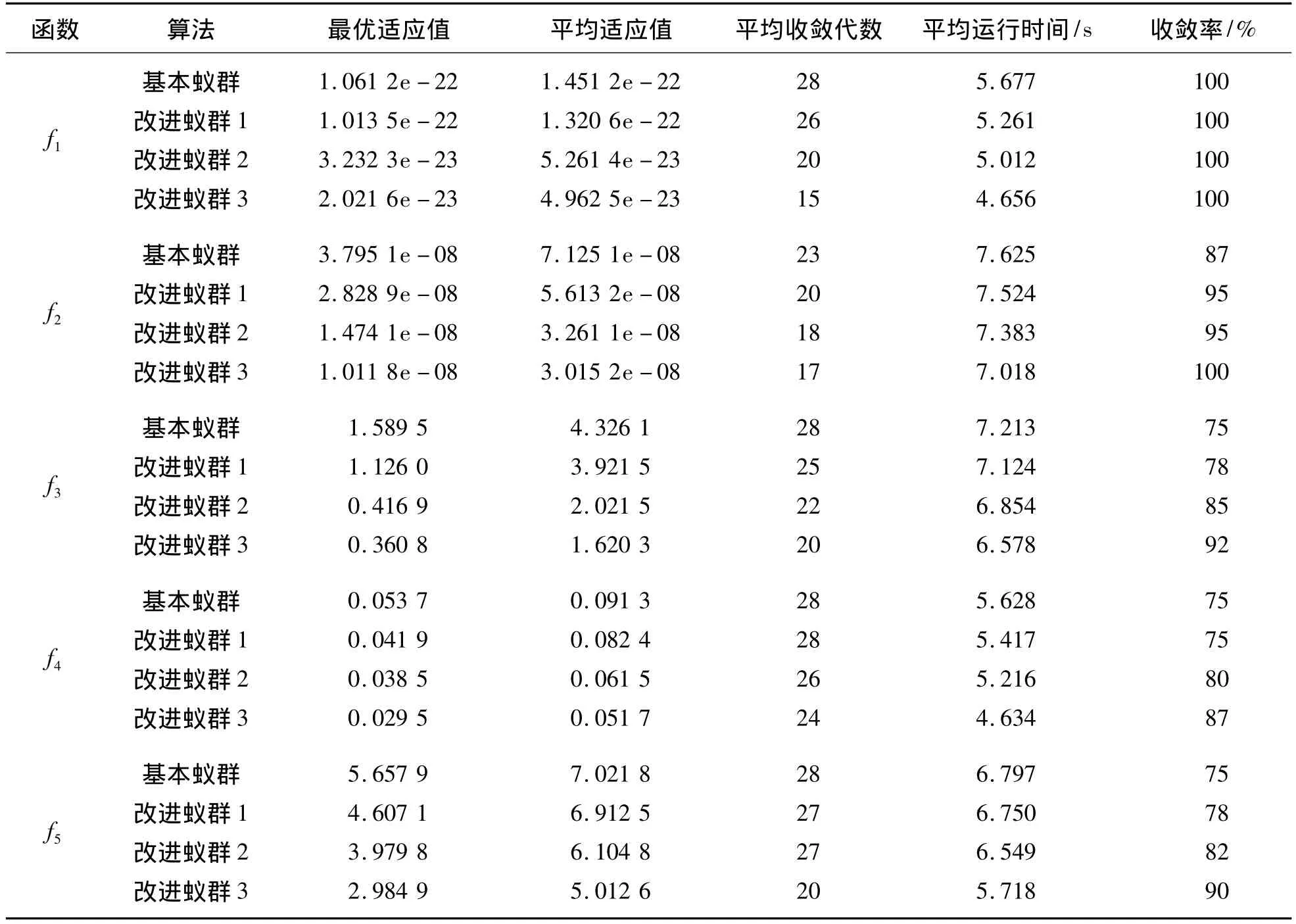
表1 基于5種基準測試函數的蟻群優化仿真結果對比Table 1 Comparison of simulation results using different ACOs based on 5 basic test functions

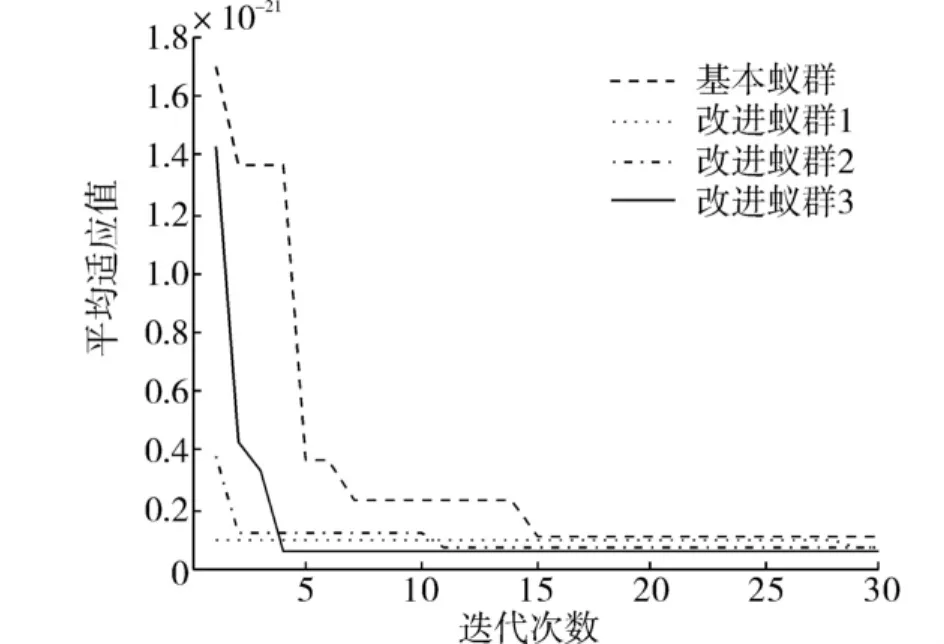
圖4 基于Sphere函數的蟻群優化仿真結果Fig.4 Simulation results of ACO based on Sphere function

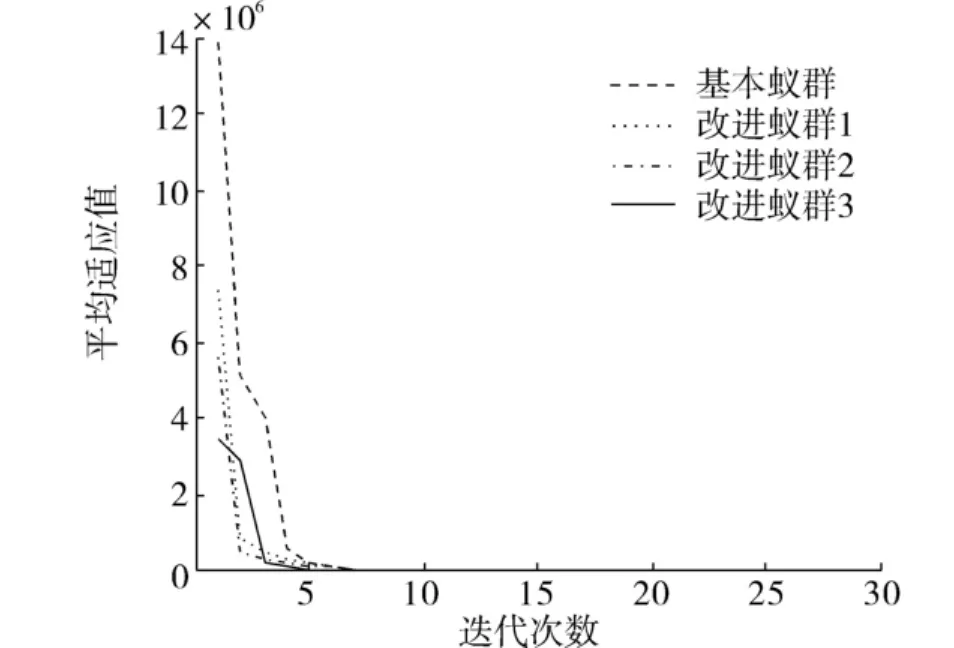
圖5 基于DeJongF4函數的蟻群優化仿真結果Fig.5 Simulation results of ACO based on DeJongF4 function

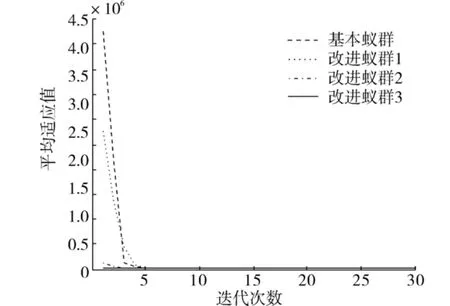
圖6 基于Rosenbrock函數的蟻群優化仿真結果Fig.6 Simulation results of ACO based on Rosenbrock function

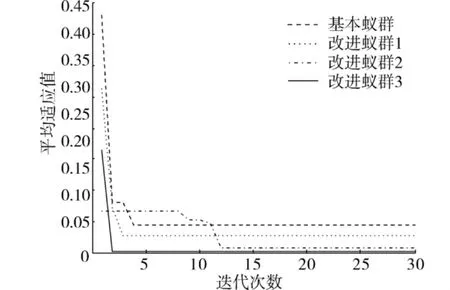
圖7 基于Griewank函數的蟻群優化仿真結果Fig.7 Simulation results of ACO based on Griewank function

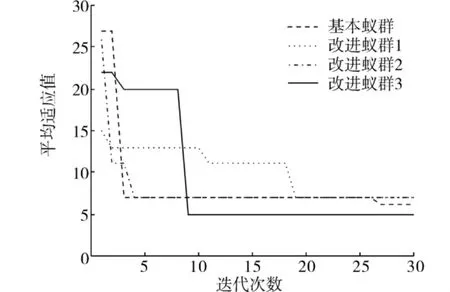
圖8 基于Rastrigin函數的蟻群優化仿真結果Fig.8 Simulation results of ACO based on Rastrigin function

根據表1及圖4～8的仿真結果可以看出，對比于文獻［5］的基本蟻群算法以及本文涉及的單個改進算法，可以得出如下結論:

1)在最優適應值和收斂時間方面，混合改進蟻群算法尋優的精度最高，并且能在最短的運行時間和最少的迭代次數內達到收斂，這是因為加入信息素揮發因子自適應策略和決策變量邊界自調整策略，逐漸縮小最優路徑和最差路徑上的信息量，實現了對決策變量空間的充分尋優.

2)在收斂率方面，在對比較難尋優的DeJongF4函數進行尋優時，混合改進蟻群算法仍然能達到100%的收斂率，對于Griewank和 Rastrigin 2個多峰函數，以及比較難尋優的Rastrigin函數進行尋優時，考慮到函數本身性能的影響，混合改進蟻群算法沒有達到100%的收斂率，但是在3種改進蟻群算法中，收斂率也是最高的，這是因為加入決策變量高斯變異策略，改善了蟻群算法的全局搜索能力，避免了局部的早熟現象.

綜上所述，本文提出的基于信息素揮發因子自適應、決策變量高斯變異和自變量邊界自調整的混合改進蟻群算法在收斂速度和收斂率方面都有很大改進，具有更好的尋優性能.

4 結束語

本文在文獻［5］蟻群算法理論的基礎上，針對蟻群算法易出現停滯現象、搜索時間長、對尋優解空間搜索不夠等不足，提出了一種基于自適應信息素揮發因子、決策變量高斯變異和決策變量邊界自調整3種改進策略的混合改進蟻群算法.將該算法應用于函數優化中，通過5個基準測試函數的仿真結果表明，本文提出的混合改進蟻群算法提高了尋優精度，加快了尋優速度，提高了收斂率，具有更好的尋優性能.

［1］DERIGO M，CARO G D.Ant algorithms for discrete optimization［J］.Artificial Life，1999，5(3):137-172.

［2］張紀會，高齊圣，徐心和.自適應蟻群算法［J］.控制理論與應用，2000，17(1):1-8.

ZHANG Jihui，GAO Qisheng，XU Xinhe.Adaptive ant colony optimization［J］.Control Theory and Applications，2000，17(1):1-8.

［3］詹士昌，吳俊.基于蟻群算法的PID參數優化設計［J］.測控技術，2004，23(2):69-71.

ZHAN Shichang，WU Jun.Design of PID optimization based on ACO［J］.Measurement＆ Control Technology，2004，23(2):69-71.

［4］李玉英.混沌螞蟻群優化算法及其應用研究［D］.北京:北京郵電大學，2009:15-21.

LI Yuying.On chaos ant colony optimization and its application［D］.Beijing:Beijing University of Posts and Tele-communications，2009:15-21.

［5］陳燁.用于連續函數優化的蟻群算法［J］.四川大學學報:工程科學版，2004，36(6):117-120.

CHEN Ye.Ant colony optimization for continuous functions［J］.Journal of Sichuan University:Engineering Science E-dition，2004，36(6):117-120.

［6］陳燁.變尺度混沌蟻群算法［J］.計算機工程與應用，2007，43(3):68-70.

CHEN Ye.On mutative scaled chaos ant colony optimization［J］.Computer Engineering and Applications，2007，43(3):68-70.

［7］王穎，謝劍英.一種自適應蟻群算法及其仿真研究［J］.系統仿真學報，2002，14(1):31-33.

WANG Ying，XIE Jianying.An adaptive ant colony optimization and its simulations［J］.Journal of System Simulation，2002，14(1):31-33.

［8］STUTZLE T，HOOS H H.MAX-MIN ant system［J］.Future Generation Computer Systems，2000，16(8):889-914.

［9］BILCHEV G A，PARMEE I C.The ant colony metaphor for searching continuous space［J］.Lecture Notes in Computer Science，1995，993(1):25-39.

［10］GUTJAHR W J.A graph-based ant system and its convergence［J］.Future Generation Computer System，2000，16(8):873-888.

［11］DREO J，SIARRY P.Continuous interacting ant colony algorithm based on dense heterarchy［J］.Future Generation Computer Systems，2004，20(5):841-856.

［12］周爽，張鈞萍，張楓，等.基于蟻群算法的遙感圖像聚類方法［J］.哈爾濱工程大學學報，2009，30(2):210-214.

ZHOU Shuang，ZHANG Junping，ZHANG Feng，et al.Clustering method for remote sensing images based on an ant colony algorithm［J］.Journal of Harbin Engineering U-niversity，2009，30(2):210-214.

［13］趙百軼，張利軍，賈鶴鳴.基于四叉樹和改進蟻群算法的全局路徑規劃［J］.應用科技，2011，38(10):23-28.

ZHAO Baiyi，ZHANG Lijun，JIA Heming.Global path planning based on quadtree and improved ant colony optimization algorithm［J］.Applied Science and Technology，2011，38(10):23-28.