一種改進的地鐵故障測距方法及應用

周文衛，陳 丹 ，陳立揚，王玉磊

0 引言

地鐵牽引網直流側發生短路故障時，為了盡快恢復牽引網供電，需要對其進行快速維修，其中故障測距對于快速定位故障位置，加快維修進度具有重要意義。

目前國內文獻對地鐵供電系統直流側故障測距介紹較少，而電力系統常用的阻抗法和行波法在地鐵供電系統中也無法直接應用。本文對目前在廣州地鐵現場運用的故障測距方法進行理論分析，并對其進行改進，提出了一種測距精度更高、操作簡單、方便快捷的故障測距方法，為現場的故障測距提供參考。

1 地鐵供電系統簡介

地鐵牽引變電所從35 kV中壓網絡引入2路電源，設2套12脈波整流機組，該整流機組的整流變壓器通過分別移相±7.5°，輸出等效24脈波直流電壓。整流機組正極通過直流快速開關與DC 1 500 V母線相連，負極與負極柜中的負母線相連[1]。地鐵供電系統通常采用雙邊供電方式，在一個供電區間內由2個牽引變電所從兩端為接觸網供電（圖1）。

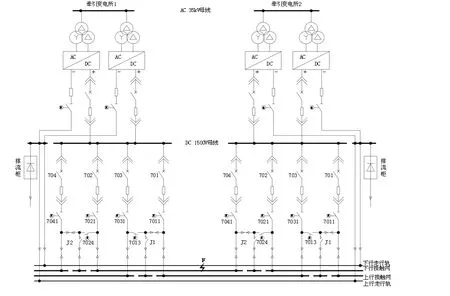
圖1 地鐵供電系統圖

2 廣州地鐵現場故障測距方法理論分析

2.1 廣州地鐵現場故障測距方法簡介

廣州地鐵 2號線采用西門子直流供電系統綜合測量和保護裝置SITRAS DPU96，將其安裝在直流饋線開關柜的二次接線處[2]，能夠將短路暫態電流和電壓數據進行記錄，并使用短路電流峰值進行粗略的故障定位。

以圖1為例，對廣州地鐵故障測距方法進行說明。假設牽引變電所1和牽引變電所2之間下行接觸網發生短路故障，故障點為F，F與牽引變電所1和牽引變電所2的距離分別為LmF和LnF，牽引變電所1的702支路記錄下的短路電流最大值為Ikm，牽引變電所2的704支路記錄下的短路電流最大值為Ikn，則認為LmF/ LnF= Ikn/ Ikm，由此可以實現故障位置的粗略定位。

2.2 理論分析

牽引供電系統仿真模型主要考慮對整流所和牽引網的處理，牽引網中接觸網和走行軌可以使用電阻串聯電感處理，而整流所可以使用直流電壓源串聯電阻和電感來處理[3]。可以建立牽引網上下行線路雙邊并列供電，接觸網發生短路時的暫態模型如圖2所示。

圖2 雙端供電的接觸網短路暫態等效電路圖

由于電感的存在，在發生短路故障時，短路電流波形的上升段呈類似于指數形式。考慮到整流所m和整流所n之間的上行接觸網總電阻為Rl，走行軌總電阻為Rrail，短路點過渡電阻為Rf，短路點F距離整流所m的距離與整流所m和整流所n間距的比值為x，在考慮短路電流穩態值時可以將圖等效并通過Δ-Y電阻等值變換而化簡為圖3（中間過程略）。

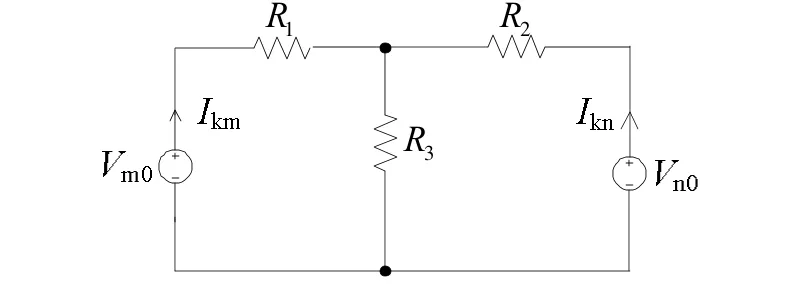
圖3 雙端供電的接觸網短路穩態等效電路簡化圖

由圖2可得到公式（1）：

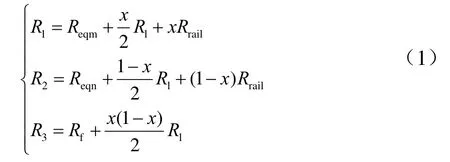
對圖 3列寫網孔電流方程并求解可以得到公式（2）：

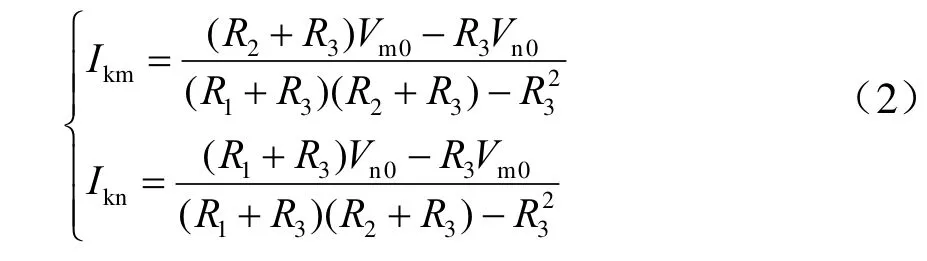
在考慮Vm0= Vn0，且Reqm= Reqn的條件下進一步可以得出兩者電流比值為

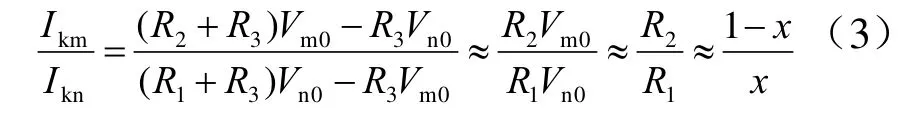
即短路點雙端穩態短路電流比值為短路點距離兩端牽引變電所距離的反比。

2.3 仿真驗證

在接觸網發生短路故障時，電流來自與接觸網連成一體的同一供電區間所有牽引變電所，為了更真實仿真短路電流，考慮短路點兩側的4個牽引變電所提供短路電流情況[4]。仿真模型中，牽引變電所由整流所模型模擬，牽引網由接觸網、走行軌模型模擬。仿真參數設置如下：架空接觸網電阻0.028 Ω/km，電感 3.424 mH/km；走行軌電阻0.023 Ω/km，電感1.78 mH/km；短路點過渡電阻Rf= 0.001 Ω；每相鄰2個整流所的間距為4 km[3]，短路故障開始的時刻為0.1 s處。建立仿真模型如圖4。

圖4 接觸網短路仿真模型圖

當短路點F距離整流所2為500 m時，從整流所2、整流所3測量的短路電流電壓波形如圖5。可以看出，當有比較大的短路電流時，整流所側電壓幅值會有明顯的降低。

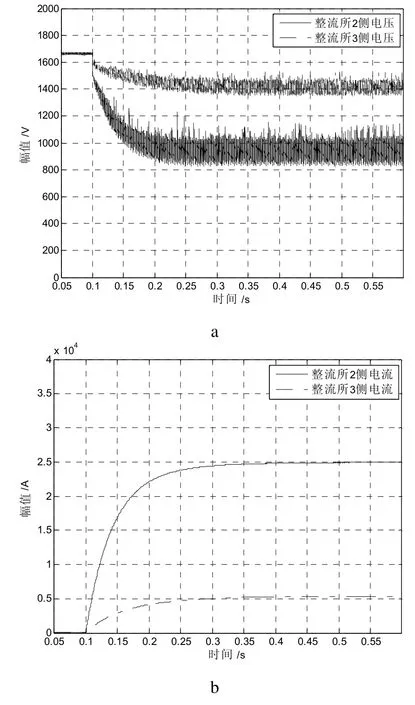
圖5 短路電壓電流波形圖

考慮短路點F距離整流所2分別為100，500，1 500 m。由于地鐵供電系統繼電保護裝置的存在，短路電流通常尚未發展到穩態值，就由于斷路器動作跳閘而逐漸降低，在仿真中并未模擬斷路器跳閘的情況。統計廣州地鐵近80組實測的短路電壓電流波形，短路電流從短路開始到跳閘完成95%以上在120 ms以內，其中電流上升段時間約為短路電流持續時間的一半，據此可以考慮電流選0.15 s時的數據將其作為故障測距使用的短路電流最大值。以圖6短路故障在距離整流所2為500 m處為例，在0.15s時刻，整流所2和整流所3的短路電流分別為16 860A，2 850 A。限于篇幅，僅將短路點F距離整流所2為500 m時的電壓電流波形給出，其余條件下，故障測距需要使用的電流僅給出數值，如表1所示。利用前述廣州地鐵現場的測距方法，測距結果如表2所列。

表1 故障測距使用的電流數據表

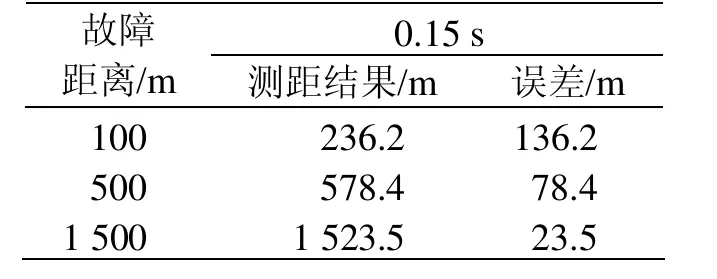
表2 廣州地鐵現場故障測距方法測距驗證表

從測距結果可以看出，當故障點越靠近兩變電所中間（遠端短路），則測距精度越高；故障點距離某一側變電所很近時（近端短路），測距精度明顯降低，測距誤差甚至達到一個供電區間長度的5%以上。而廣州地鐵現場運營經驗表明，測距誤差為線路長度10%左右，這比仿真測距誤差大。

3 改進的故障測距方法

考慮到在近端短路時，前述故障測距方法精度不高，從前述推導可以看出，這是由于忽略了一系列條件的結果。考慮到整流所的外特性，其直流輸出端電壓隨著負荷電流的變化，呈非線性特性，通常使用多段折線描述24脈波整流機組的外特性[5]。本文使用的整流機組外特性曲線如圖6所示。

圖6 整流機組外特性曲線圖

可以看出，輸出負荷電流差別很大時，對應于外特性曲線上，直流輸出電壓差別很大。以圖6短路點在500 m處，0.15 s時的數據為例，此時整流所2的負荷電流為16 860 A，平均直流輸出電壓為1100.2 V；而對應的整流所3的負荷電流為2 850 A，平均直流輸出電壓為1 512.5 V。而公式（3）的推導中，直接考慮Vm0= Vn0。這也解釋了，當發生遠端短路時，由于2座變電所負荷電流相近，Vm0= Vn0大致成立，因而測距精度較高；而發生近端短路時，由于短路點兩側變電所負荷電流相差太大，則并不成立，測距精度比較低。

考慮對測距方程進行改進如下：

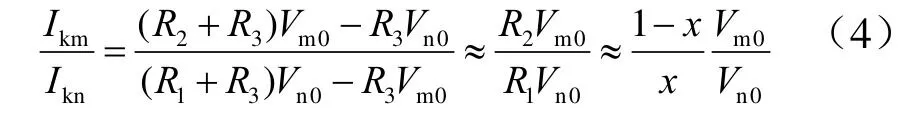
電流仍使用表1的數據，電壓數據的選取和電流類似，但是由于電壓是24脈波直流電壓，因而在取0.15 s電壓值時，可以取0.15 s所在脈波的電壓采樣數據平均值作為 0.15 s時的直流電壓輸出值。電壓數據如表3所示。利用式（4）的測距方程測距結果如表4。

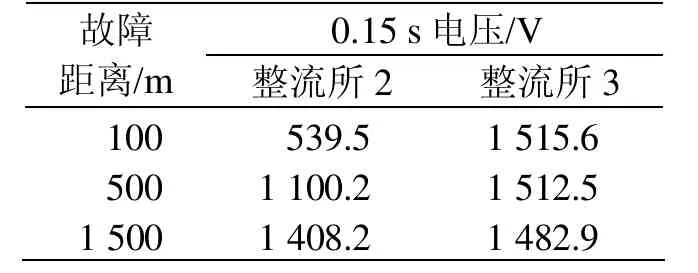
表3 故障測距電壓數據表

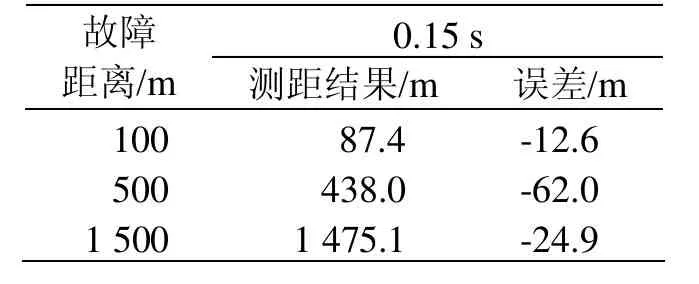
表4 改進后故障測距方法測距驗證

從表4可以看出，對于遠端短路故障，改進后的方法測距精度略有改善；對于近端短路故障，改進后的方法測距精度明顯提高。總體的測距誤差基本控制在±60 m的范圍內。

4 結論

本文介紹了廣州地鐵現場使用的一種粗略的故障測距方法，對其進行理論分析和仿真驗證。并在其基礎上對測距方法進行改進，改進后的方法對于近端短路情況改善非常明顯，對遠端短路略有改善。廣州地鐵現場故障測距方法和本文的改進方法在仿真時，存在的前提條件是，短路點雙端變電所的電壓電流數據是時間同步的。SITRAS DPU96裝置在現場只能記錄電壓電流數據，而無法對雙端數據進行時間同步。當發生近端短路時，靠近故障點的直流快速開關因大電流脫扣動作可以迅速跳閘，并將跳閘信號通過聯跳導線傳送至對端變電所，使對端變電所的直流快速開關立即跳閘[6]，其中延時時間可達數毫秒，因而雙端記錄的短路電流最大值并不在同一時刻，由此將造成測距精度比仿真時略有降低。

[1] 張健，肖書印，張友鵬.地鐵供電系統短路試驗的仿真分析[J].都市快軌交通，2008，（8）.

[2] 劉華輝.SITRAS DPU96在廣州地鐵2號線的應用[J].機車電傳動，2005，（3）.

[3] 李良威.城市軌道交通直流側短路故障研究[D].成都：西南交通大學，2007.

[4] 劉煒.城市軌道交通列車運行過程優化及牽引供電系統動態仿真[D].成都：西南交通大學，2009.

[5] 劉煒，李群湛，李良威.基于多折線外特性模型的直流牽引供電系統穩態短路計算[J].機車電傳動，2008，（1）.

[6] 李墨雪.直流牽引供電系統建模及基于電流變化特征量的保護算法研究[D].北京：北京交通大學，2010.