改進的粒子群優化算法

閆文靜, 鄒書蓉, 張洪偉

（成都信息工程學院計算機學院,四川成都 610225）

0 引言

粒子群優化算法（Particle Swarm Optimization,PSO）是由Kennedy和Eberhart（1995年）首次提出的一種基于迭代的尋優算法[1],源于對生物界中鳥群覓食行為的研究,是一個基于群體智能（Swarm Intelligence,SI）的優化算法。PSO算法具有簡潔性,易于實現,收斂速度快,需要調節的參數少等優點,一經提出便得到快速的發展。PSO算法已經在函數優化、神經網絡訓練、模式分類、模糊系統控制、求解大規模組合優化問題等各個領域的取得了大量的有效成果[2]。

在對PSO算法的研究過程中發現其存在易于陷入局部最優及早熟收斂等缺陷,針對這些問題許多學者提出了一些改進方案,例如w線性遞減策略[3],通過反復試驗,建議w=0.9線性遞減到0.4的策略,這樣使得粒子群算法早期具有良好的全局搜索能力,能快速定位到接近全局最優點的區域,后期則具有良好的局部搜索能力,能精確得到全局最優解。雜交PSO模型[4]將進化算法中的交叉操作引入PSO算法,使后代繼承了雙親粒子的優點,加強了粒子間區域的搜索能力,有效擺脫局部最優。混沌粒子群優化模型[5],以目前整個粒子群所搜索到的最優位置為基礎,利用混沌運動的遍歷性去產生一個混沌序列,然后將產生序列中的最優位置的粒子隨機地代替目前粒子群中的一個粒子,這樣可以使粒子能有效地擺脫局部極值點,提高算法尋找全局最優點的能力。免疫粒子群優化算法[6]中機體能特異的識別“非己”和“自己”的刺激,保留記憶反應的能力,可以避免粒子群算法陷入局部最優的缺點。

針對PSO算法易于陷入局部最優的缺陷,提出了一種在引入自適應慣性權重基礎上的新的進化模型的粒子群優化算法（New mode Particle Swarm Optimization,NPSO）。通過仿真實驗與其他改進算法的比較表明,提出的新算法具有很好的收斂精度,能有效避免陷入局部最優及早熟收斂現象。

1 粒子群算法的基本原理

粒子群優化算法的基本概念源于鳥群捕食的過程,在PSO算法中,每個優化問題的解都看作是搜索空間中一個粒子,所有的粒子都有一個由被優化的函數決定的適應度值。PSO算法先初始化一群隨機粒子,每個粒子的屬性由速度vi（vi=（v1,v2,…,vD））,位置 xi（xi=（x1,x2,…,xD））來描述。在下一個時間點到來的時候,所有的粒子都是通過跟蹤兩個“極值”來更新其速度,這兩個極值分別為個體局部極值（pbest）即粒子自身找到的最優解;全局極值（gbest）即整個群體找到的最優解。再通過優化問題所決定的適應度函數去評價新的粒子的優劣程度。粒子更新速度和位置公式如下:

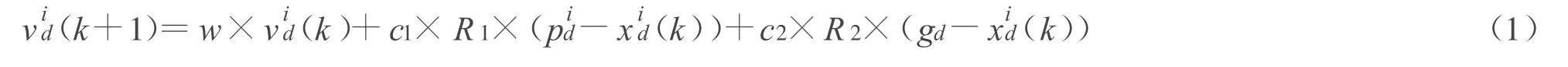
2 粒子群算法的改進

2.1 PSO算法局部收斂性判斷

全局最優值取決于個體最優值的變化,在迭代過程中,當前迭代的全局最優值總是要優于或至少等于上一次迭代所得的全局最優值。PSO算法在迭代過程中,粒子都是通過跟蹤兩個極值更新自己。即在找到這兩個最優值后,粒子按照式（1）和（2）確定自己下一時刻的速度和位置。常規的粒子群算法中粒子都是向著一個方向在飛行,假如在飛行過程中遇到了局部極值點,全體粒子的速度將快速的下降為零從而聚集在局部最優停止飛行,這樣粒子就陷入了局部極值點。為此改進PSO算法時,引入進化速度因子h,如果優化目標是尋極大值,F（gbestk）≥F（gbestk-1）,則定義h=F（gbestk-1）/F（gbestk）;反之,F（gbestk）≤F（gbestk-1）,則定義進化速度因子h=F（gbestk）/F（gbestk-1）;于是

根據上面的定義,進化速度因子0＜h≤1。在整個迭代過程中進化速度因子h的值與進化速度成反比,即h值越小,進化速度越快。一定迭代次數后,若h=1,代表算法找到了最優解或者停滯陷入了局部最優。此時將得到的最優解gbest與理論全局最優解（或期望最優解）做比較,可以判斷出此時得到的最優解是否為陷入局部最優的解。大量的實驗數據表明,h大于Δ（如0.2～0.5）時判斷粒子陷入局部最優的可能性最大,在此應設法使粒子跳出局部最優的位置,使粒子能在搜索空間里繼續搜索尋優。

2.2 粒子的聚集度

根據上面的定義粒子聚集度因子0＜s≤1,s值能有效反映當前所有粒子的聚集程度,同時也可反映出粒子的多樣性。大量實驗數據表明s的值與粒子的聚集程度成正比,即s值越大,粒子群的聚集度越大,這樣表明粒子多樣性越小。若s的值為1,則斷定粒子群中的所有粒子具有同一性,如果驗證此時的粒子為陷入局部最優,粒子將很難跳出該極值點。

2.3 自適應的慣性權值

慣性權重w是PSO算法中的一個重要參數,被用于調節粒子過去對現在的影響程度。Shi和Eberhart研究慣性權重w對優化性能的影響發現:較大的慣性權重能增強全局探索能力,較小的慣性權重能提高局部發掘能力有利于算法收斂。為此進行了大量的研究工作,先后提出了隨機慣性權值（RIW）策略[7]、線性遞減權值（LDW）策略[8]和模糊慣性權值（FIW）策略[9]。目前比較流行的做法是線性遞減策略LDW,公式如下所示:

上式中,ws和we表示慣性因子的初始值和結束值,t表示當前次數,tmax表示迭代的最大次數。在優化方程性能上有明顯效果,但是LDW中的w只與迭代的次數線性相關,因此不能適應算法運行中的非線性變化、復雜等特性。

研究w發現,慣性權重的值應該伴隨著粒子群進化速度和粒子的聚集程度而變化[10],所以w可以表示為h和s的函數,即 w=f（h,s）。分析可知如果粒子群的進化速度降低時,此時減小 w的值,使算法在小空間范圍內進行搜索,這樣能較快地找到算法的最優解。如果粒子群的進化速度加快時,加大 w的值,使得粒子群在較大的空間內持續搜索尋優。若粒子在搜索空間里分布的比較分散,此時粒子群就不易陷入到局部最優,但是伴隨著粒子群聚集度的逐漸升高,粒子將很容易陷入到局部最優,此時為提高粒子群的全局尋優能力應及時地加大粒子群搜索的空間。根據上面的分析可知,w值大小應該伴隨著粒子的聚集度的加快而增大,相應的,也應伴隨著粒子群進化速度的減慢而減小,w可以表示為:

wini為w 的初始值,通常 wini的值為1。由于0＜h≤1,0＜s≤1,wini-wh＜w ＜wini+ws。

2.4 改進的粒子群進化模型

為了使PSO算法避免“早熟”收斂現象[11],提出將陷入局部最優的粒子向群體最優的反方向飛行,這樣便于粒子跳出局部最優并在解空間大范圍飛行尋優。其速度迭代公式不變,位置迭代進化更新公式如下所示:

式（7）即是改變粒子尋優的飛行方向[12],使粒子能在大范圍開拓搜索空間中尋優。提出的改進的粒子群優化算法的流程如下,粒子群迭代先是按照標準模型即式（1）、（2）進化,判斷h值的大小,若發現粒子陷入局部收斂時,立即使用式（1）、（7）迭代進化,使粒子能及時跳出局部最優,在解空間里大范圍搜索尋優。這樣處理可以有效地防止“早熟”收斂,提高算法的全局收斂性能。

3 算法流程

綜上所述,新算法流程如下:

（1）初始化。設定PSO算法的參數（N,c1,c2,ws和we等）,隨機產生初始種群及每個粒子的速度和位置,計算每個粒子的適應值并排序。并初始化種群的全局最優值和個體最優值,并將粒子的pbest設置為當前位置,gbest設置為初始群體中最佳粒子的位置。

（2）根據式（1）、（2）更新每個粒子的速度和位置。

（3）重新計算粒子的適應度,按適應值排序,按照式（3）、（4）、（6）計算新的 h、s和w 。

（4）根據式（3）判斷進化速度因子h值的大小,若大于Δ時,轉向（4）,否則轉向（5）

（5）按式（1）、（7）更新每個粒子的速度和位置。

（6）若算法未達到最大允許迭代次數,迭代次數I=I+1返回（2）,否則轉到（6）。

（7）停止優化并輸出結果。

4 算法仿真實驗

表1給出了實驗中運用4個經典測試函數,用這4個函數來仿真測試驗證文中所提出算法的尋優能力,并將結果與標準PSO 、LDWPSO算法、NPSO算法進行對比分析。

表1 測試函數

f 1至 f4函數的最優值都是0,測試時4種算法的種群粒子數各取50,LDWPSO中慣性權重ws=0.8,we=0.1,c1=c2=2,h=0,s=0。測試函數維數為30,最大迭代次數500,測試3種算法所達到的精度。所有仿真實驗都是通過Java語音編程,并對仿真結果作對比。對3種算法分別進行50次實驗,表2給出了測試4個經典函數所達到精度的平均值。

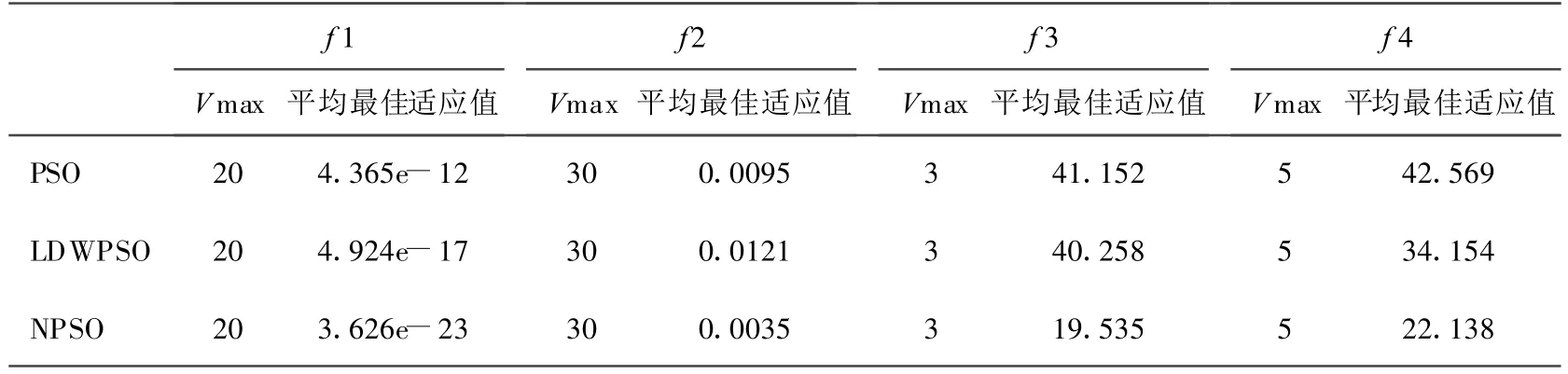
表2 4個經典函數的測試結果

從表2可以看出,新算法相對于其他兩個算法在平均最佳適應值上有明顯提高,這說明新算法的優化能力得到了明顯的提高。為了反映新算法性能的改善,對這4個經典的函數分別進行250次迭代,算法收斂圖,如圖1～4所示。

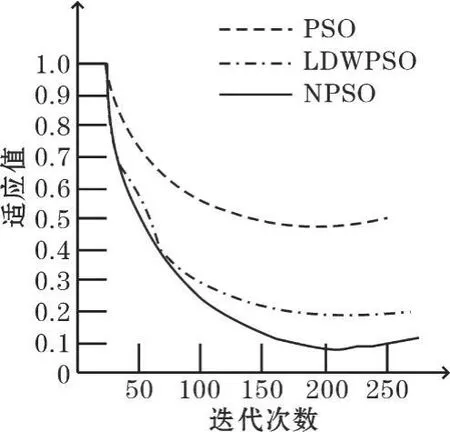
圖1 Sphere函數收斂示意圖

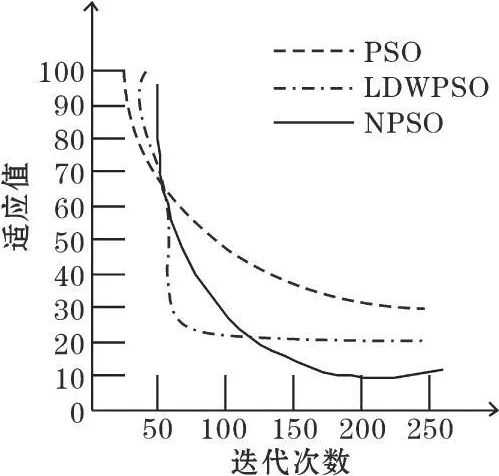
圖3 Rastrigrin函數收斂示意圖

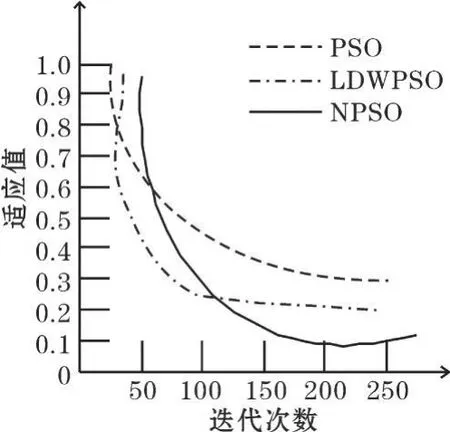
圖2 Griewank函數收斂示意圖

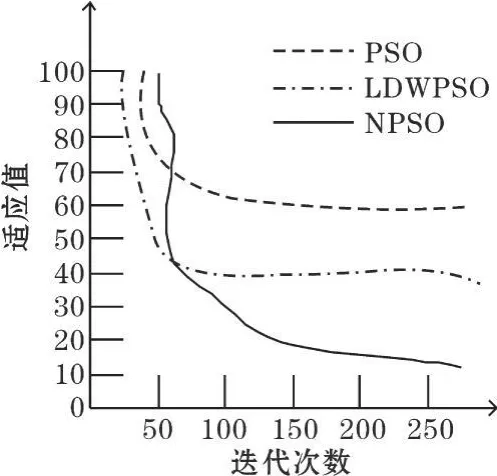
圖4 Rosenbrock函數收斂示意圖

從圖1～4經典函數的收斂圖可以直接看出,NPSO算法明顯優于基本粒子群算法和LDWPSO算法。算法的收斂性優于經典算法,充分體現了改進的優勢。

5 結束語

為有效抑制和避免PSO算法早熟收斂,提出的新進化模式的粒子群優化算法原理為:在采用自適應慣性權重的基礎上,通過判斷粒子是否陷入局部最優,對陷入局部最優的粒子群采用新的進化模型,從而使粒子迅速跳出局部最優,在更大的空間里尋優,這樣可以保證算法能夠有效避免早熟收斂和陷入局部最優。通過對4個經典函數的測試,顯示出改進的粒子群優化算法具有更好的收斂精度,能有效避免粒子陷入局部最優。若應用到實際優化問題上將起到很好的推動作用。

[1] KENNEDY J,EBERHART R C.Particle Swarm Optimization Proceedings of 1995[C].IEEE International Conference on Neural Networks,1995:1942-1948.

[2] Eberhar t RC,Shi Y H.Particle swarm optimization:developments,applications and resources[A].Proceedings of the IEEE Congress on Evolutionary Computation[C].Piscataway,USA:IEEE Service Center,2001.

[3] Shi Y,Eberhart RC.Empirical study of particle swarm optimization[C].Proceedingsof the IEEE Congresson Evolutionary Computation,2009.

[4] Wetter M.and Wright J.A comparison of deterministic and probabilistic optimization algorithms for nonsmoth simulation-based optimization[J].Building and Environment.2006.

[5] 李兵,蔣慰孫.混沌優化方法及其應用[J].控制理論與應用,2007,14.

[6] 段富,蘇同芬.免疫粒子群算法的改進及應用[J].計算機應用,2010,30:1883-1884.

[7] R Eberhart,Y Shi.Tracking and optimizing dynamic systems with particle swarms[A].The IEEE Congresson Evolutionary Computation[C].San Francisco,USA:IEEE,2001.

[8] Y Shi,R Eberhart.Empirical study of particle swarm optimization[A].International Conference on Evolutionary Computation[C].Washington,USA:IEEE,2002.

[9] Y Shi,R Eberhart.Fuzzy adaptive swarm optimization[A].The IEEE Congress on Evolutionary Computation[C].San Francisco,USA:IEEE,2001.

[10] 劉懷亮,高鷹,許若寧,等.一種新的改進粒子群優化方法[J].計算機工程與應用,2010,46.

[11] 李寧,鄒彤,孫德寶,等.基于粒子群的多目標優化算法[J].計算機工程與應用,2005,41.

[12] 俞歡軍.混合粒子群游湖算法研究[J].信息與控制,2005,34.