未知信源數目的DOA估計方法

李鵬飛 鐘子發 張 旻

(合肥電子工程學院309研究室 合肥 230037)

(安徽省電子制約技術重點實驗室 合肥 230037)

1 引言

在現代電子戰信號環境中，由于信號密度大，信號形式復雜，使得電子偵察中的信號處理任務越來越困難。對無線電測向提出了高精度、高分辨率、解相干信號等方面的要求。最經典的波達方向(DOA)估計方法是利用波束在空間掃描來確定目標的方向，但是它無法分辨兩個很近的空間信號。以MUSIC(MUltiple SIgnal Classification)[1]算法為代表的空間譜估計方法突破了瑞利限，可以達到很高的精度。該類算法一般要求信源數目精確已知，當估計的信源數與真實信源數不一致時，會對信源方位的估計產生嚴重影響。同時在存在相干信號時，其性能嚴重下降，雖然可以通過空間平滑的方法進行解相干，但是陣列孔徑損失嚴重。

信號稀疏分解作為一種新出現的信號分析思想，可以得到信號的一個非常簡潔的表達(即稀疏表示：sparse representation)，已經在諸多應用領域體現出其優勢[2-5]。陣列信號的空間譜并不是連續的，也就是說僅僅存在少數幾個非零值分別代表著相應的空間方位。空間信號的這種稀疏特性，決定了我們可以用稀疏分解的方法進行DOA估計。利用稀疏分解的方法進行D O A估計具有以下的優點[6-10]：(1)具有很高的分辨率和估計精度；(2)不需要進行任何預處理，可以直接應用到相干信號上來；(3)對初始值的選擇不是很敏感。利用快拍數據的稀疏分解進行DOA估計容易受到噪聲的影響。Malioutov等人[10]提出了l1-SVD(l1norm Singular Value Decomposition)的方法進行DOA估計，即對陣列接收數據進行奇異值分解(SVD)，然后利用l1范數約束求解稀疏解得到目標的估計值。l1-SVD方法克服了快拍數據稀疏分解容易受到信號噪聲影響的缺點，但是該方法需要已知信源數，當信源數過估計時，性能嚴重下降。

針對以上問題，本文提出了兩種不需要估計信源數目的DOA估計方法。一種基于特征向量稀疏分解(Eigen Vector Sparse Decomposition,EV-SD)的DOA估計方法，采用協方差矩陣最大特征值對應的特征向量來代替陣列快拍數據作為稀疏分解向量，可以有效減少噪聲及信號幅度跳變的影響，和l1-SVD算法相比不需要估計信源數目，增強了算法的魯棒性。另一種基于協方差矩陣高階冪稀疏分解(High Order Power Sparse Decomposition,HOPSD)的DOA估計方法。首先證明了陣列接收數據的協方差矩陣的高階冪的列向量是所有信號方向矢量的線性組合，因此可以利用其列向量的組合建立DOA估計的稀疏模型。該方法避免了估計信號源數目和特征值分解。

2 數學模型

2.1 陣列信號的數學模型

假設來波方向為θi(i=1,…,p)的p個遠場信號入射到M元天線陣列，t時刻第l個陣元的接收信號為

τli為第l陣元相對參考陣元的延遲，寫成矢量形式為

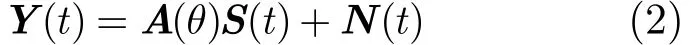
式中Y(t)為t時刻采集的M×1維的陣列快拍數據矢量；A(θ)為M×p維的陣列導向矢量矩陣，A(θ)=[a(θ1),a(θ2),…,a(θp)];S(t)為t時刻的p×1維的空間信號矢量；N(t)為M×1維的陣列噪聲數據矢量；其中，導向矢量為

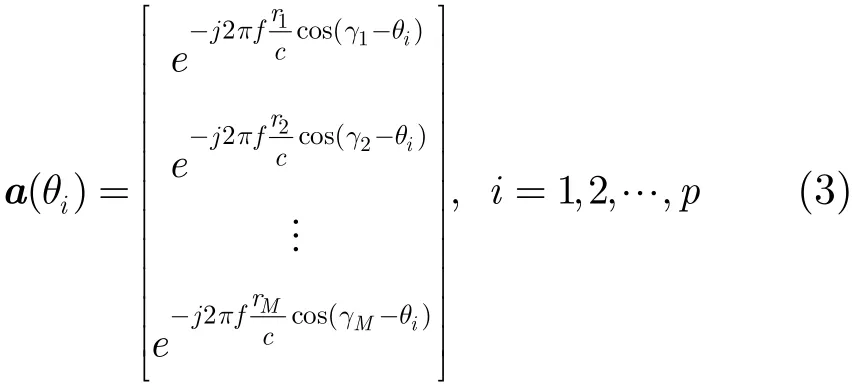
式中rl(l=1,2,…,M)為陣列參考點和陣元n距離，γl(l=1,2,…,M)為陣元l相對參考點的極坐標角度，c為電磁波傳播的速度。

2.2基于稀疏表示的DOA估計模型

稀疏表示進行 DOA估計的主要思想是將信號的陣列流型矩陣擴展成一個過完備的冗余字典D，它包含了所有可能的源位置信息。令θ={θ1,θ2,…,θN}代表所有可能的源位置的一個采樣集合，θn代表信號的到達角度(DOA)，方向矩陣A可擴展成如下的過完備字典：

定義N×1的信號向量h={h1,h2,…,hN}，當且僅當源信號位于角度θn處，hn有非零值，其他分量均為零，可以得到DOA估計的稀疏模型：

利用基追蹤(Basic Pursuit,BP)[11]等稀疏分解算法求得h，根據h中非零元素的位置可以得到信號的DOA。直接利用式(5)進行稀疏分解進行DOA估計，容易受到噪聲的影響。文獻[10]提出l1-SVD的方法進行DOA估計。即對式(2)陣列的接收數據采集多個快拍，然后對這些快拍數據進行奇異值分解，取其中的p個較大奇異值對應的奇異向量的線性組合作為式(5)待分解的向量Y。

3 未知信源數下的DOA估計方法

3.1基于陣列協方差矩陣特征向量稀疏分解的DOA估計方法(EV-SD算法)

l1-SVD方法需要估計信號源的數目，本文利用多快拍數據估計陣列輸出的協方差矩陣，然后對協方差矩陣作特征值分解，利用最大特征值對應的特征向量作為待分解的數據向量，來實現 DOA估計，避免了估計信源數目。

多采樣信號可以表示成如下形式：

利用L個快拍數據得到陣列的協方差矩陣估計值。

對R做特征值分解得

如果信號協方差矩陣的秩為K(K≤p)，假設噪聲協方差矩陣RN為滿秩矩陣，則有如下線性關系[12]：

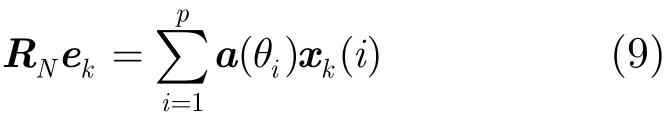
其中1≤k≤K,ek為特征矢量，xk(i)為線性組合因子。當噪聲協方差矩陣為理想白噪聲時，式(9)即簡化為

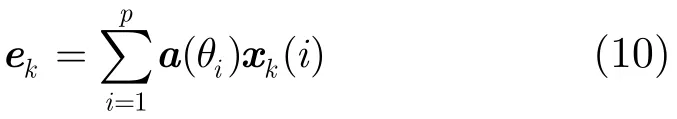
式(10)說明無論信號源是否相干，最大特征值對應的特征矢量是各信號源方向矢量的一個線性組合。令協方差矩陣的最大特征值為emax，則

參照式(4)對a(θi)進行擴展，形成冗余字典D，得到特征向量的稀疏模型：

對式(12)進行稀疏分解得到h,h中非零元素的位置就代表了空間目標的方位信息。不同于基于快拍數據稀疏分解的 DOA估計方法，特征值分解減弱了噪聲的影響，而選取最大特征值對應的特征向量進一步減弱了噪聲的影響，因此本文方法在低信噪比情況下魯棒性較好。

3.2 基于陣列協方差矩陣高階冪稀疏分解的DOA估計方法(HOP-SD算法)

EV-SD方法雖然不需要估計信號源的數目，但是計算過程中的特征值分解計算量較大。因此本文提出一種不需要特征值分解和估計信號源數目的DOA估計方法。對陣列協方差矩陣R做特征值分解：

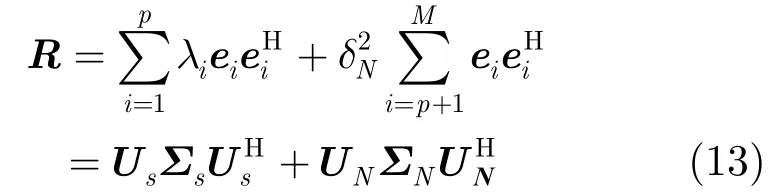
式中∑s為大特征值組成的對角陣，∑N為小特征值組成的對角陣。Us=[e1,e2,…,ep]為大特征值對應的信號子空間，UN=[ep+1,…,eM]為小特征值對應的噪聲子空間(信號為獨立信號時，p為信號個數；存在相干信號時，p為協方差矩陣的秩)。由式(13)可得

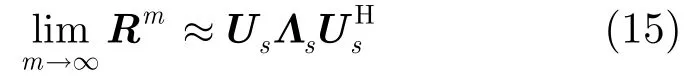
實際應用時，在一定信噪比條件下，m取有限整數就能獲得很好的收斂性能。令Rm=[r1,r2,…,rM],rm為M×1維的列向量。根據式(15)，則

其中(·)i表示取向量的第i個元素。從式(16)可以看出，ri是所有大特征向量的線性組合。將協方差矩陣高階冪的所有列向量相加，形成一個新的向量：

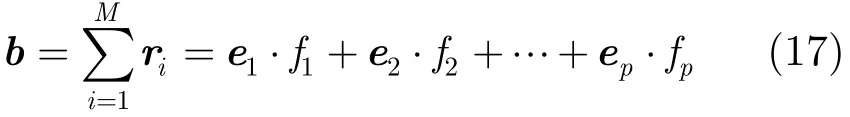
其中fi(i=1,2,…,p)代表組合系數。式(10)說明無論信號源是否相干，大特征值對應的特征矢量是所有信號方向矢量的一個線性組合。由式(17)和式(10)可知，協方差矩陣高階冪的所有列向量的和向量b是所有信號方向矢量的一個線性組合。即

參照式(4)對a(θi)進行擴展，形成冗余字典D，得到特征向量的稀疏模型為

對式(19)進行稀疏分解得到h,h中非零元素的位置就代表了空間目標的方位信息。不同于l1-SVD方法，本文提出的HOP-SD算法不需要特征值分解，計算量較小。同時不需要估計信號源的數目，增強了算法的魯棒性。

3.3 稀疏正則化方法

由式(12)或式(19)求得h的過程實際上是一個反問題，反問題的特點亦為其難點就是：它們在Hadamard定義下是不適定的，即在反問題中我們不能完全保證解的存在性、唯一性和穩定性。通常利用正則化方法解決此類問題。盡可能地保證近似解的穩定性的基礎上，保留解的盡可能多的信息。由于信號的稀疏特性，使得我們可以找到充分稀疏的唯一解，而且通過這個稀疏擴展就可以精確重構原信號[13,14]。

找到最好的、也就是最稀疏的信號表示，等同于解決下述問題：

其中是序列h中非零項的個數。從一個隨機冗余字典中尋找信號的稀疏擴展是一個 NP難問題，為解決這一難點，Chen等人[11]將其轉化為解決下述稍有差別的問題：

當上述模型含有噪聲時，式(21)的約束條件不再適用，問題轉化為最小化目標函數：

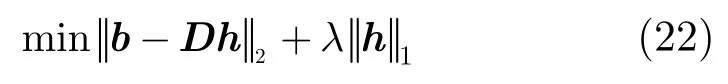
目標函數中前一項反映失配程度，后一項反映稀疏性要求，λ為正則化參數。由于h是復數，它的l1范數為

可以發現式(23)的兩邊平方仍不能消除平方根項，直接導致我們不能使用二次規劃的方式最小化目標函數。為了解決這個問題，我們采用二階錐規劃的方法，其轉化形式為

利用內點法可以有效解決上述優化問題，得到式(19)中稀疏分解的系數，進而根據非零元素的位置求得信源的DOA估計值。式(22)或式(24)的求解需要參數λ的值，λ的取值不同，所得估值可能不同。故估計式(22)的關鍵是如何選擇合適的參數λ。L-曲線法是較成熟的方法，以對數為橫坐標，為縱坐標，并以正則化參數λ為參變量得到類似于“L”形狀的擬合曲線圖，即。“L”曲線上曲率最大的那點對應的λ值是L-曲線的最優值。圖1為式(24)的“L”曲線，根據圖1中曲率最大的點可以得到最優的正則化參數λ=0.26。在下文的仿真實驗中，正則化參數為0.26。

4 實驗及性能分析

實驗1 HOP-SD算法中冪指數的選取

HOP-SD算法利用陣列協方差矩陣的高階冪提取信號子空間作為特征分解的向量，理論上冪指數趨近于無窮大才能收斂到信號子空間，為了分析冪指數m對算法的性能影響，做如下實驗：假設來波方向在0～180°內隨機產生的2個獨立信號入射到5元均勻線陣上，陣元間距為半波長，分別采用不同的冪指數計算 DOA估計的均方根誤差隨信噪比變化曲線，每個信噪比下進行1000次獨立實驗(如圖2所示)。

從圖2可以看出，在較低信噪比(-10 dB)的情況下，較小的冪指數不能使算法收斂到令人滿意的程度，均方根誤差達到 2.2°。隨著冪指數的增大，算法逐漸收斂，冪指數大于等于5時，收斂效果較好，估計的均方根誤差小于1°。因此實際應用時，冪指數m取有限整數就能獲得很好的收斂性能。下文的仿真實驗中，m=5。

實驗2 對獨立信號的分辨率和估計精度

為了驗證算法對兩個間隔很近信號的分辨能力，作如下定義：如果對兩個信號的估計誤差在1°以內，則認為能成功分辨，否則不能分辨。在信噪比15 dB下，2個獨立信號入射到5元均勻線陣上，陣元間距為半波長。圖3是不同角度間隔下的分辨概率。每個角度間隔下進行1000次獨立實驗。圖4是不同信噪比下的均方根誤差，信號的來波方向在0～180°內隨機產生，每個信噪比下進行 1000次獨立實驗。

從圖3可以看出，本文提出的HOP-SD和EVSD算法對非相干信號具有較高的分辨率，能分辨出很近的兩個信號，分辨性能明顯優于MUSIC算法。在低信噪比下EV-SD算法稍優于HOP-SD算法。從圖4可以看出，本文提出的方法具有較高的估計精度。在信噪比為-10 dB時，均方根誤差小于1°，和l1-SVD方法接近，優于MUSIC算法。

實驗3 相干信號的分辨率和估計精度

在信噪比15 dB下，2個相干信號入射到5元均勻線陣上，陣元間距為半波長。圖5是不同角度間隔下的分辨概率。每個角度間隔下進行1000次獨立實驗。圖6是不同信噪比下的均方根誤差，信號的來波方向在0～180°內隨機產生，每個信噪比下進行1000次獨立實驗。

圖1 L曲線圖

圖2 不同冪指數下的均方根誤差隨信噪比變化曲線

圖3 不同角度間隔下的分辨概率(非相干信號)

從圖5可以看出，本文提出的 HOP-SD和EV-SD算法對相干信號同樣具有較高的分辨率，能分辨出很近的兩個信號，在低信噪比下EV-SD算法稍優于HOP-SD算法。而MUSIC算法在相干信號存在的情況下，分辨性能嚴重下降。從圖6可以看出，本文方法對相干信號同樣具有較高的估計精度。在信噪比為-10 dB時，均方根誤差小于 1°。而MUSIC算法在存在相干信號時，性能嚴重下降。

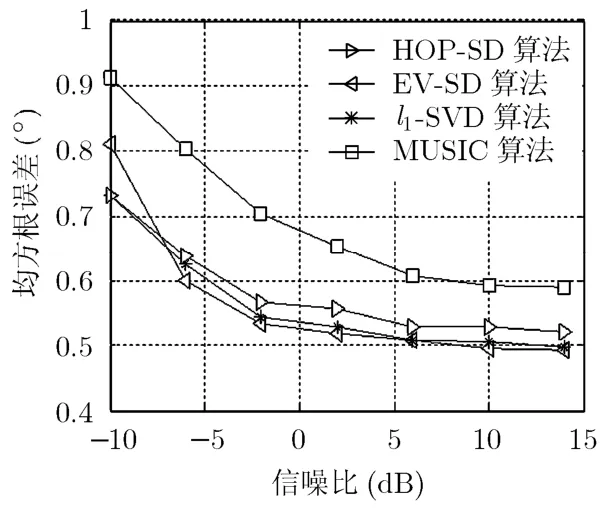
圖4 不同信噪比下的均方根誤差(非相干信號)

圖5 不同角度間隔下的分辨概率(相干信號)

圖6 不同信噪比下的均方根誤差(相干信號)

實驗4 信號源過估計和欠估計時性能

假設來波方向在0～180°內隨機產生的2個獨立信號入射到5元均勻線陣上，陣元間距為半波長，分別采用l1-SVD算法和本文方法計算DOA估計的均方根誤差隨信噪比變化曲線，每個信噪比下進行1000次獨立實驗。圖7是信源過估計時的估計精度比較，圖8是信源欠估計時的估計精度比較。

從圖7可以看出：當信源過估計時，l1-SVD算法的估計精度嚴重下降，而本文提出的HOP-SD和EV-SD算法不受信源數估計正確與否的影響，不受其影響。從圖8可以看出，信源數欠估計時，對l1-SVD算法和本文方法的影響并不大。這主要是因為，信源數欠估計時，l1-SVD算法作為稀疏分解的奇異向量，仍然包含在信號子空間中，并且含有所有信號方向矢量的成分(證明參考式(10))。

5 結論

論文研究了兩種基于稀疏分解的 DOA估計方法，理論分析和仿真實驗結果驗證所提算法具有很高的分辨率和估計精度，同時能夠適用于相干信號，不同于l1-SVD方法，本文提出的方法不需要估計信號源的數目，增強了算法的魯棒性。其中， EV-SD算法的分辨能力和估計精度在低信噪比下稍優于HOP-SD算法。冗余字典的構造和快速高效的稀疏分解算法是稀疏分解在DOA應用中的難點和關鍵，目前適用于多維 DOA估計的冗余字典的構造正在深入研究之中。

圖7 信源過估計時的均方根誤差

圖8 信源欠估計時的均方根誤差

[1]Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas Propagation,1986,34(3)：276-280.

[2]Samadi S,Cetin M,Masnadi-Shirazi M A,et al..Sparse representation-based synthetic aperture radar imaging[J].IET Radar,Sonar＆Navigation,2011,5(2)：182-193.

[3]Namgook C and Kuo C C J.Sparse MUSIC representation with source-specific dictionaries and its application to signal separation[J].IEEE Transactions on Audio,Speech,and Language Processing,2011,19(2)：326-337.

[4]Dai D and Yang W.Satellite image classification via two-layer sparse coding with biased image representation[J].IEEE Geoscience and Remote Sensing Letters,2011,8(1)：173-176.

[5]Namgook C and Kuo C C J.Sparse representation of musical signals using source-specific dictionaries[J].IEEE Signal Processing Letters,2010,17(11)：913-916.

[6]Gao Xiang-yun and Zhang Tian-qi.Multi parameter estimation of wideband chirp signals based on OMP decomposition[C].IEEE International Conference on Information Theory and Information Security,Beijing,Dec.17-19,2010：722-727.

[7]Md Mashud Hyder and Kaushik Mahata.Direction-of-Arrival estimation using a mixedl2,0norm approximation[J].IEEE Transactions on Signal Processing,2010,58(9)：4646-4655.

[8]Guo Xian-sheng,Wan Qun,Chang Chun-qi,et al..Source localization using a sparse representation framework to achieve superresolution[J].Mulitidimensional Systems and Signal Processing,2010,21(4)：391-402.

[9]Zhang Shu,Li Yu-mei,and Song Jun-cai.A novel method for DOA estimation based on generalized-prior distribution[C].2010 International Conference on Measuring Technology and Mechatronics Automation,Changsha,China,2010：244-247.

[10]Malioutov D,Cetin M,and Willsky A S.A sparse signal reconstruction perspective for source localization with sensor arrays[J].IEEE Transactions on Signal Processing,2005,53(8)：3010-3022.

[11]Chen Hao-bing,Donoho D L,and Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Joumal on ScientificCompting,2001,20(1)：33-66.

[12]Cadzow J A,Kim Y S,and Shiue D C.General direction-ofarrival estimation：a signal subspace approach.IEEE Transactions on Aerospace and Electronic Systems,1989,25(1)：31-46.

[13]Donoho D and Huo X.Uncertainty principles and ideal atomic decompositions[J].IEEE Transactions on Information Theory,2001,47(7)：2845-2862.

[14]Elad M and Bruckstein A M.A generalized uncertainty principle and sparse representation in pairs of bases[J].IEEE Transactions on Information Theory,2002,48(9)：2558-2567.