一類具有常數避難所與收獲率的捕食－食餌模型的穩定性分析

周稻祥，朱長榮

(重慶大學數學與統計學院，重慶 401331)

捕食－食餌模型一直都是生物數學研究的重要領域。近年來，由經典的捕食－食餌模型衍生出很多帶各種新參數的種群模型，因為這些模型更能反映現實世界的真實狀況，因此，引起了人們的廣泛關注［1－119］。在這些模型中，帶食餌避難所的捕食－食餌模型是重要的一種。研究結果指出:避難所在捕食者和食餌相互作用中發揮著穩定性的作用，并且避難所參數對系統的動力行為發揮著重要影響［2－9］。Olivares 和 Jiliberto［2］提出了如下的帶食餌避難率的捕食者－食餌的種群模型:

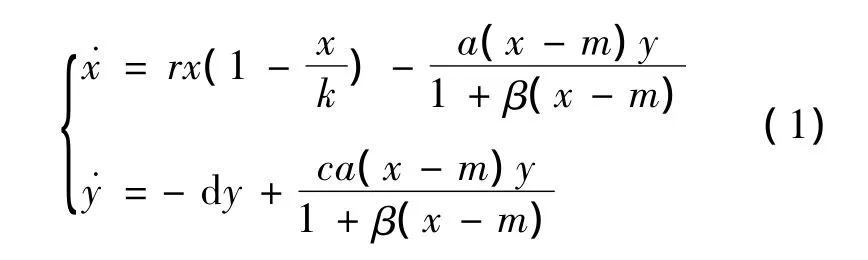
其中:所有參數均非負;x和y分別表示在時間t的食餌和捕食者的種群密度;r表示食餌的內稟增長率;k表示最大環境容量;c表示轉化率;a(xm)y/(1+β(x－m))表示HollingⅡ功能反應函數;d是捕食者的死亡率;m表示食餌避難所。

系統(1)已有很多研究結果［2，6－7］。文獻［2］利用微分方程定性理論的方法指出系統(11)有3個平衡點，內部平衡點是局部漸近穩定的，而且證明了極限環的存在性。文獻［6］通過構造Dulac函數研究了系統(1)的全局穩定性，且用Poincare-Bendixson定理證明了極限環的唯一性。

在生物數學中，考慮到生物鏈的健康性、可持續性以及生物鏈產生的效益，近期有很多學者研究了帶收獲率的生物模型［13－14］。朱天曉［13］考慮了具有線性收獲率的生物模型:

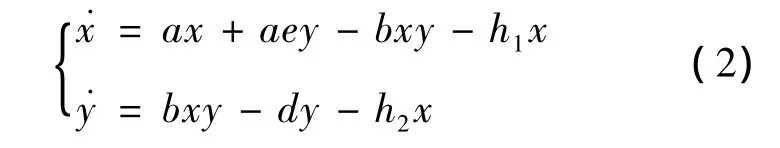
其中h1、h2為捕獲強度。文獻［13］利用微分方程定性理論，給出了系統(2)的平衡點的穩定性條件，通過構造Dulac函數的方法，利用Bendixson-Dulac判定定理，證明了系統(2)不存在極限環。

在模型(1)和(2)的基礎上，本文研究帶線性功能反應曲線、常數食餌避難所和線性收獲率的捕食－食餌模型。具體來說，本文考慮以下的捕食－食餌模型:

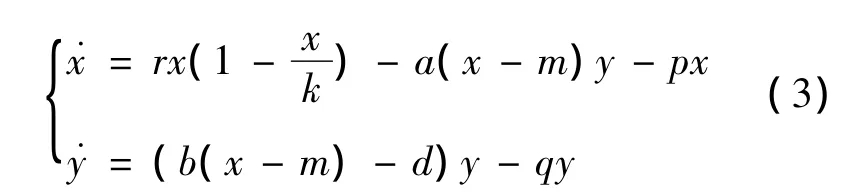
其中:x、y、r、k、d 的生物意義和模型(1)一樣;(x －m)y表示線性功能反應函數;a、b為捕食系數;px、qy表示線性收獲率。

本文討論了系統(3)的全局與局部動力性態。利用Gronwall不等式，證明了系統(3)的解的一致有界性。利用平面系統的動力性質理論，研究了系統(3)的平衡點的類型及穩定性。分析發現:系統在第1象限及其邊界上至多有3個平衡點，其中2個為邊界平衡點，1個為內平衡點。邊界平衡點可以為雙曲鞍點、雙曲結點，也可以為非雙曲的鞍－結點;內平衡點的動力性態較豐富，對不同的參數取值范圍，可以是穩定結點、穩定焦點。證明了內平衡點的全局穩定性。最后進行了數值模擬，模擬結果與理論結果完全吻合。

1 系統解的一致有界性

因為生物系統中的捕食者與食餌的數量都非負，而且系統(3)帶有食餌避難率，因此x＞m。實際上，系統(3)在 Ω ={(x，y)|x＞m，y ＞0}中是一致有界的。

定理1 系統(3)在Ω中的解一致有界。

證明 令W=x+ay/b。對方程兩邊關于時間求導，并將式(3)代入，可得

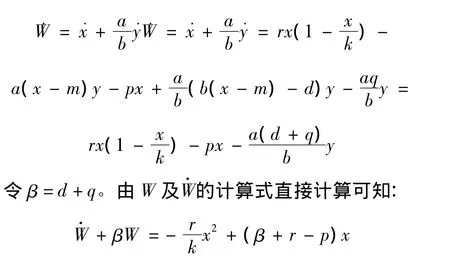
上式右邊是一個開口向下的二次函數，當 x=k(β +r－p)/2r時+βW 達到最大值:

上式中令 t→∞，有0＜W ＜μ/β，即系統(3)的解是一致有界的。

定理1表明，系統(3)中捕食者和食餌的初始種群密度在Ω中，捕食者和食餌的種群密度都降落在Ω的一個有界集內。這表明捕食者和食餌可以在Ω中長期共存。

2 平衡點的動力性態

本節將研究系統(3)的動力性態。很顯然，x軸的正半軸是系統(3)的不變流形，y軸的正半軸不是系統(3)的不變流形，但是在y軸的正半軸上點的向量場是(+，－)，所以經過y軸正半軸的軌線，都要從第2象限進入到第1象限。因而，第1象限及其邊界是系統(3)的不變集。下面將在第1象限及其邊界上討論系統(3)的動力性態。

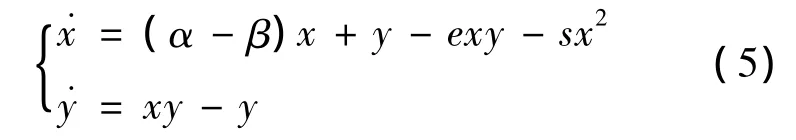
其中 α =r/ρ，β =p/ρ，e= ρ/bm ＞1，s=r/bk。

平衡點在討論系統的動態行為時起著十分重要的作用，對平衡點的動力行為的研究關系著系統的局部穩定性、全局穩定性等。分2種情況計算系統(5)的平衡點。

1)當y=0時，系統有2個平衡點:A=(0，0)和B=((α －β)/s，0)。注意到 α=β時，A與B 重合，并且捕食者與食餌均非負，因此B存在，當且僅當α＞β。所以僅在α＞β的條件下討論系統(5)在B處的動力性態。

2)當y≠0時，系統有平衡點C=(x*，y*)=1，(α－β－s)/(e－1())。注意到x*＞0，y*＞0，且e＞1，所以C在第1象限內，當且僅當α＞β+s。因此僅在α＞β+s的條件下，討論系統(5)在C處的動力性態。

在討論平衡點的動力性態時，平衡點處的雅可比矩陣起著重要作用。令(x0，y0)是系統(5)的平衡點，則系統(5)在平衡點處的雅可比矩陣為

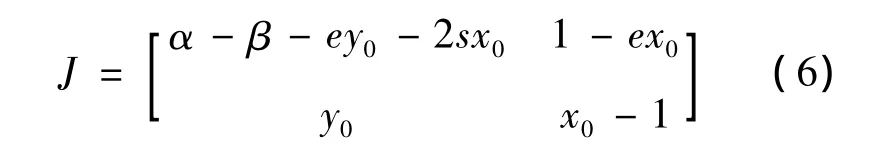
首先討論平衡點A處的動力性態。

定理2 1)當 e＞1，s＞0，α ＞β＞0時，A為不穩定鞍點;2)當 e＞1，s＞0，0＜α＜β時，A為穩定結點;3)當 e＞1，s＞0，α=β＞0時，A為鞍 －結點。

證明 系統(5)在平衡點A處的雅可比矩陣為

所以特征值為:λ(A)1= －1＜0，λ(A)2=α－β。

1)當e＞1，s＞0，α ＞β＞0時，有 λ(A)2＞0，則A為不穩定鞍點。

2)當e＞1，s＞0，0＜α ＜β時，有 λ(A)2＜0，則A為穩定結點。

3)當e＞1，s＞0，α=β＞0時，有，在平衡點 A處作變換 x=u－v，y=v，則系統(5)的變為

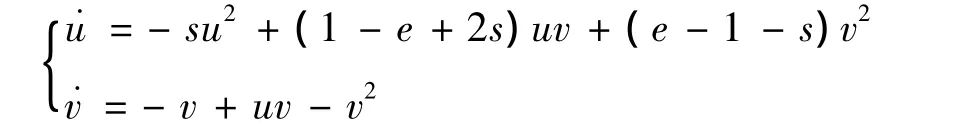
依照文獻［8］中2.11的定理1知A是鞍－結點。

因為平衡點B存在，當且僅當α＞β，在α＞β的條件下考慮B點處的動力性態。

定理3 1)當 e＞1，s＞0，α ＞s+β 時，B 為不穩定鞍點;2)當 e＞1，s＞0，β＜α ＜β+s時，B 為穩定結點;3)當 e＞1，s＞0，α=β+s時，B 為鞍 －結點。

證明 系統(5)在平衡點B處的雅可比矩陣為

所以特征值為:λ(B)1= －(α －β)＜0，λ(B)2=(α － β)/s－1。

1)當e＞1，s＞0，α ＞s+β 時，有 λ(B)2＞0，則B為不穩定鞍點。

2)當e＞1，s＞0，β ＜α ＜β+s時，有 λ(B)2＜0，則B為穩定結點。

3)當 e＞1，s＞0，α =β +s時，λ(B)2=0，且平衡點B=(1，0)。將平衡點 B移到原點，令 x=u+1，y=v，則系統化為

對系統(7)引入變換 u=x+(1－e)y，v=sy，則系統(7)變為

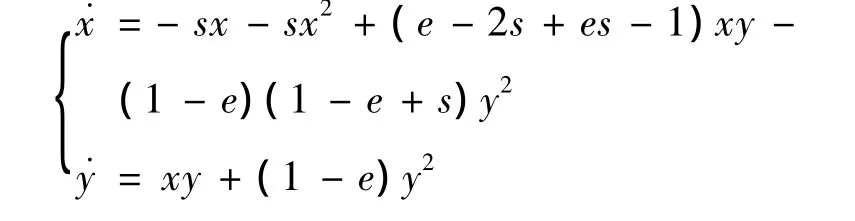
依照文獻［8］中2.11的定理1知B是鞍－結點。

最后，因為C在第1象限內，當且僅當α＞β+s，所以在α＞β+s的條件下討論系統(5)在C處的動力性態。

定理4 1)當 s＞0，β+s＜α≤β+s+s2/4，e＞1時，C 為穩定結點;2)當 s＞0，β+s+s2/4＜α時，令e0=(α－β－s)/(2－s)＞0，則:① 如果1＜e≤e0+1，則C為穩定結點;② 如果e＞e0+1，則C是穩定焦點。

證明 系統(5)在平衡點C處的雅可比矩陣為

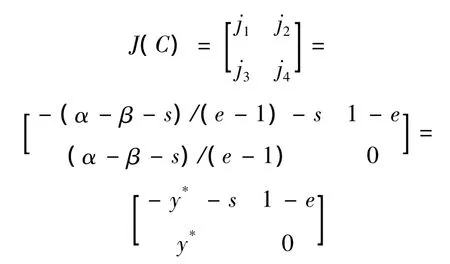
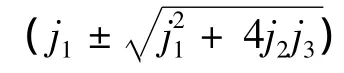
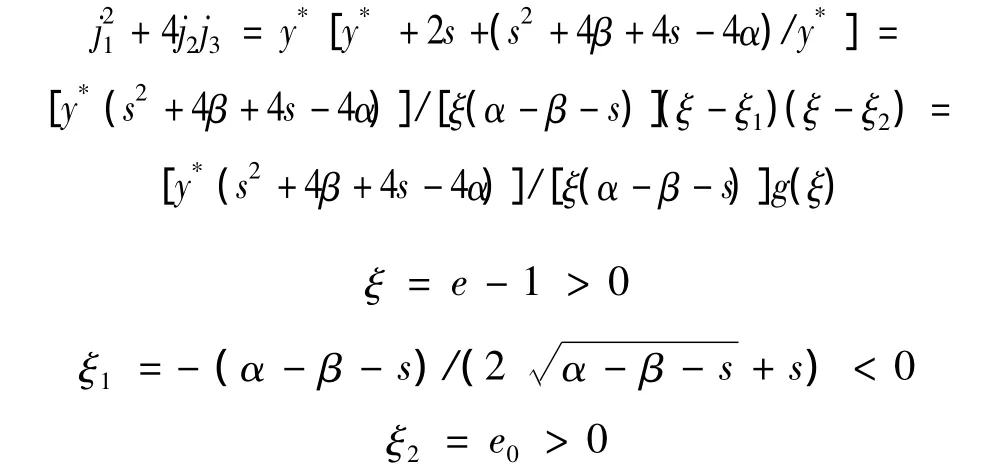
1)當 s＞0，β+s＜α≤β+s+s2/4，e＞1時，+4j2j3≥0，λ(C)1、2為負實數，故 C 為穩定結點。

2)當s＞0，β+s+s2/4＜α時，注意到ξ＞0且+4j2j3和 g(ξ)的符號相同，有下面的結論:① g(ξ)≥0，當且僅當0 ＜ξ≤ξ2，即1 ＜e≤e0+1，則λ(C)1、2為負實數，故 C 為穩定結點;② g(ξ)＜0，當且僅當 ξ＞ξ2，即e＞e0+1，則λ(C)1、2為具有負實部的復數，故C是穩定焦點。

從定理4看到，內部平衡點C總是局部漸近穩定的。實際上，還能得到C點的全局穩定性:當s＞0，α ＞β+s，e＞1時，平衡點 C 是全局穩定的。這是因為:將平衡點C移到原點，令x=u+x*，y=v+y*，則系統(5)化為

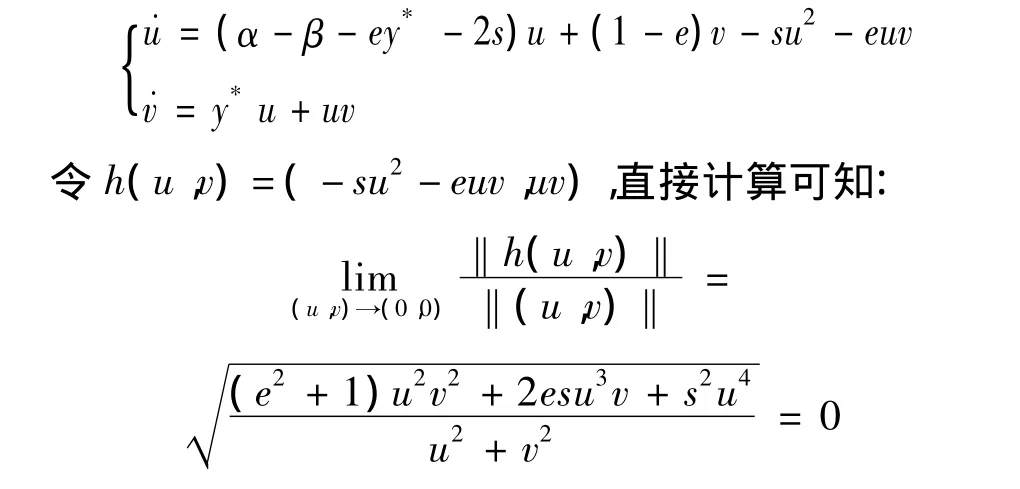
由文獻［4］中定理10.6知平衡點 C是全局穩定的。

3 數值模擬

現在通過數值模擬來驗證理論分析結果。為了模擬此系統，令 α =0.469，β =0.352，e=2.13，s=0.0166，得到系統在平衡點C(1，0.088849)處是漸近穩定的。在初值為(2，0.3)時得到的相圖見圖1。捕食和食餌隨時間的變化見圖2。捕食者和食餌隨時間的變化見圖3、4。

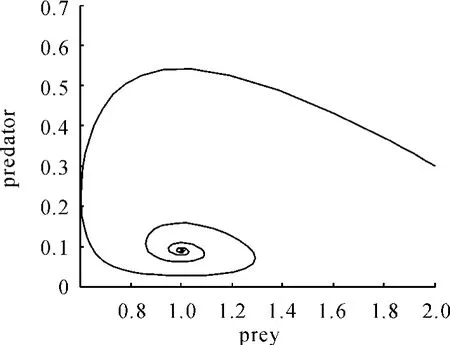
圖1 系統(5)在平衡點C(1，0.088849)處的相圖

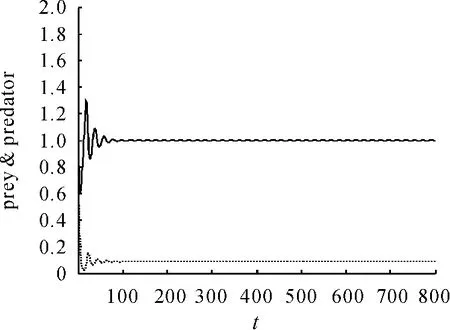
圖2 捕食和食餌隨時間的變化

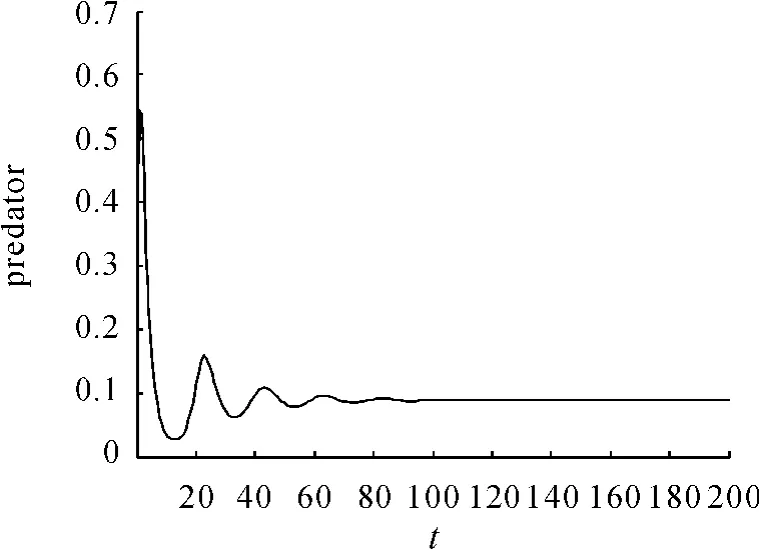
圖3 捕食隨時間的變化

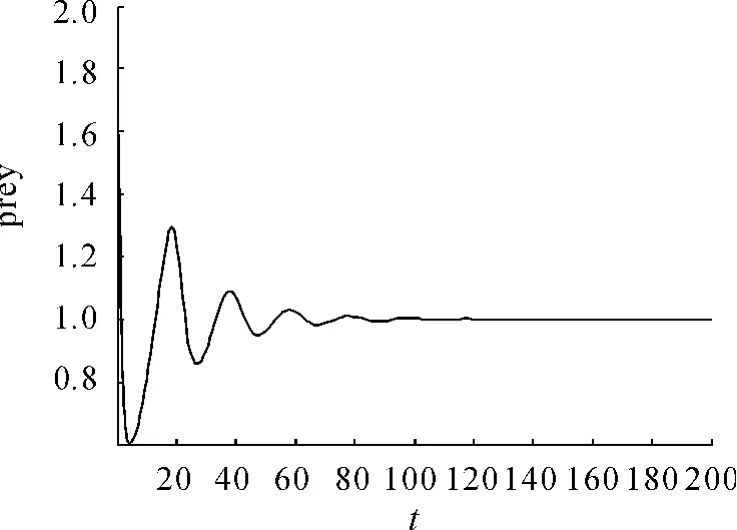
圖4 食隨時間的變化

4 結束語

本文進行了系統解的一致有界性以及平衡點穩定性的定性分析。分析指出增加避難所的數量就可以增加食餌的密度，且穩定性和動態行為受到避難所參數m的影響，內部平衡點C是全局穩定的，即無論開始捕食和食餌的數量是多少，最終將要穩定在一定的數量之內。數值模擬也很好地印證了這些結果。

［1］Birkoff G，Rota G C.Ordinary differential equations［M］.Ginn:［s.n.］，1982.

［2］González-Olivares E，Ramos-Jiliberto R.Dynamic consequences of prey refuges in a simple model system:More prey，fewer predators and enhanced stability［J］.Ecological Modeling，2003，166:135 －146.

［3］Dai G，Tang M.Coexistence region and global dynamics of a harvested predator-prey system［J］.SIAM Journal on Applied Mathematics，1998(1):193 －210.

［4］Grank J，Martin H G，Melluish D M.Nonlinear ordinary differential equations［M］.USA:［s.n.］，1977.

［5］Yuri K.Elements of Applied Bifurcation Theory［M］.Second Edition.New York:Springer，1998:79 －100.

［6］Chen L，Chen F.Qualitative analysis of a predator prey model with Holling type II functional response incorporating a constant prey refuge［J］.Nonlinear Analysis Real World Applications，2008(10):125 －127.

［7］Ji L L，Wu C Q.Qualitative analysis of a predator-prey model with constant-rate prey harvesting incorporating a constant prey refuge［J］.Nonlinear Analysis Real World Applications，2010(11):2285 －2295.

［8］Perko L.Differential Equation and Dynamical Systems［M］.Sencond Edition.New York:Spinger，1996:146－152.

［9］Kar T K.Modeling and analysis of a harvested prey-predator system incorporating a prey refuge［J］.Journal of Computational and Applied Mathematics，2006，185:19－33.

［10］Kar T K.Stability analysis of a prey-predator model incorporating a prey refuge［J］.Communications in Nonlinear Science and Numerical Simulation，2005(10):681－691.

［11］Tao Y D，Wang X，Song X Y.Effect of prey refuge on a harvested predator-prey model with generalized functional response［J］.Commun Nonlinear Sci Numer Simulat，2011，16:1052 －1059.

［12］張芷芬，丁同仁，黃文灶，等.微分方程定性理論［M］.北京:科學出版社，1985:49－90.

［13］朱天曉.具有線性收獲率的Diekman模型穩定性［J］.長春大學學報，2007(3):1－4.

［14］劉娟，李醫民.兩種群都有收獲率的微分生態系統的定性分析［J］.徐州師范大學學報，2011(2):32－35.

［15］趙琳，雒志學，王利紅.在容量較小的污染環境中種群的最優捕獲問題［J］.重慶理工大學學報:自然科學版，2011，25(2):122 －126.

［16］張靖.食餌具有流行病的捕食－被捕食(SIS)模型的分析［J］.四川兵工學報，2011(9):153－156.

［17］張志軍，劉啟寬，李映輝.具有線性收獲率且包含食餌避難所的一類食餌－捕食者模型的定性分析［J］.重慶理工大學學報:自然科學版，2011，25(9):104－113.

［18］李盈科，樊小琳，陳亮.帶有非線性傳染率的階段結構捕食食餌模型的持久性［J］.四川兵工學報，2011(7):151－154.

［19］劉啟寬，羅廷友，李映輝.一類具功能反應且常數投放的食餌－捕食系統的定性分析［J］.重慶理工大學學報:自然科學版，2011，25(3):1118 －122.