考慮軌道攝動的外熱流計算分析

王宇寧，魏 承，趙 陽

（哈爾濱工業(yè)大學(xué) 航天學(xué)院，黑龍江 哈爾濱 150001）

0 引言

作為航天器在軌道空間的主要熱源，軌道外熱流計算成為航天器熱分析與熱設(shè)計的基礎(chǔ)。目前，外熱流計算主要有能束均勻分布法、積分法、隨機模擬法和蒙特卡洛法等。文獻［1］基于蘭貝特余弦定律和能量守恒定律，推導(dǎo)了均勻布置能束發(fā)射點和發(fā)射方向上能束的能量計算公式，但由于實際物體輻射不滿足蘭貝特定律，其實用性、可擴展性較差。積分法通過球面三角關(guān)系求解外熱流角系數(shù)并積分，不能考慮多曲面間遮擋［2］。文獻［3］采用隨機模擬法，隨機選取地球表面面積元，用球面三角關(guān)系計算該面元對空間飛行器表面上任一微元面的地球反照和紅外輻射角系數(shù)，而后大量選取面元并以累加代替積分，但并未解決遮擋問題。蒙特卡洛法因其通用性、擴展性強，易解決遮擋問題，易與節(jié)點網(wǎng)絡(luò)法結(jié)合，而成為外熱流計算的主要方法，得到了廣泛應(yīng)用［4－5］。但目前多數(shù)文獻均使用角系數(shù)計算外熱流，僅考慮入射外熱流被直接吸收部分，未對外熱流的多次反射和吸收作深入研究。

在外熱流計算中，國外熱分析軟件忽略了軌道攝動和太陽矢量變化的影響，導(dǎo)致其瞬態(tài)外熱流計算存在較大誤差。如Thermal Desktop軟件，在確定入軌參數(shù)后只計算初始軌道由平近角或真近角確定的給定位置處的外熱流，而計算瞬態(tài)溫度場時，則反復(fù)輸入已計算外熱流進行迭代。應(yīng)用熱分析軟件進行熱設(shè)計時，一般根據(jù)瞬態(tài)溫度場的計算結(jié)果驗證熱設(shè)計的有效性和合理性。因外熱流計算不準確，導(dǎo)致瞬態(tài)溫度場計算存在誤差，致使熱設(shè)計有效性的驗證缺乏可靠依據(jù)。為彌補目前該領(lǐng)域的不足，便于與節(jié)點網(wǎng)絡(luò)法結(jié)合，本文對考慮軌道攝動的外熱流計算進行了研究。

1 外熱流角系數(shù)及輻射傳遞因子定義

在輻射熱傳遞相關(guān)領(lǐng)域中，曲面Ai到曲面Aj的角系數(shù)定義為曲面Ai投射到曲面Aj輻射熱流量與曲面Ai發(fā)出的總輻射熱流量之比。溫度場數(shù)值計算中的節(jié)點網(wǎng)絡(luò)法常用熱流量建立熱平衡方程，故該曲面間角系數(shù)定義方式可很好地與節(jié)點網(wǎng)絡(luò)法結(jié)合。

由于軌道外熱流的特殊性，太陽、地球總輻射熱流量計算不易，傳統(tǒng)外熱流角系數(shù)均定義為外熱流密度與外熱流強度之比，為無量綱數(shù)，不利于輻射傳遞因子概念的導(dǎo)出以及與節(jié)點網(wǎng)絡(luò)法結(jié)合。為此，本文將外熱流角系數(shù)定義為投射外熱流量與外熱流強度之比。

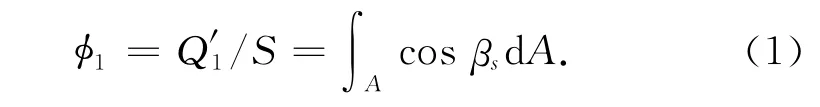
式中：βs為微元面dA外法線與太陽照射方向夾角。

定義地球紅外輻射角系數(shù)為投射到航天器面元的地球紅外輻射外熱流量與地球平均紅外輻射強度Ei0之比。對航天器面元A，地球紅外輻射角系數(shù)可表示為

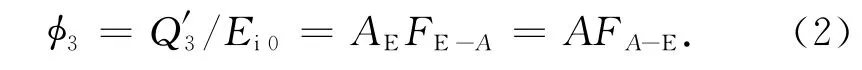
式中：AE為地球表面積；FE－A為地球表面到航天器面元的角系數(shù)；FA－E為航天器面元到地球表面角系數(shù)。另有

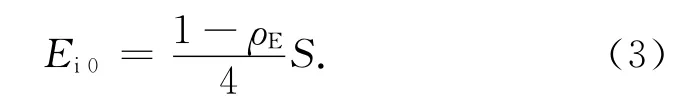
式中：ρE為地球表面平均反射率。地球反照輻射角系數(shù)定義為投射到航天器面元的地球反照輻射外熱流量與地球平均反照輻射強度Er0之比。對航天器面元A，地球紅外輻射角系數(shù)可表示為

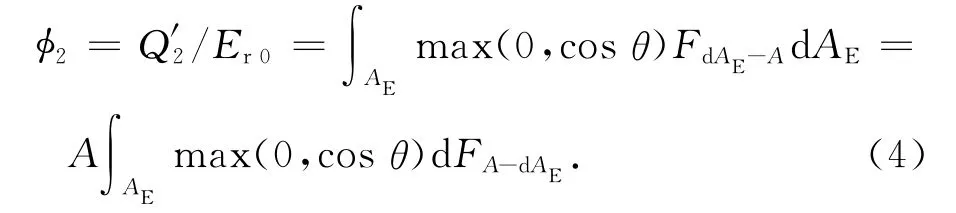
式中：dAE為地球表面任一微元面積；θ為太陽矢量與dAE外法線的夾角；為微元面dAE到航天器面元A的角系數(shù)；為A到dAE的角系數(shù)。FE－A，F(xiàn)A－E，均為一般意義的輻射換熱角系數(shù)［6］。Er0＝ρsS。

用外熱流輻射傳遞因子可較好地計算考慮多次反射后航天器表面單元（簡稱面元）吸收外熱流，其定義為航天器面元實際吸收外熱流量與相應(yīng)外熱流輻射強度之比。根據(jù)研究對象不同，又分為太陽輻射傳遞因子、地球紅外輻射傳遞因子及地球反照輻射傳遞因子。計算輻射傳遞因子時，傳統(tǒng)蒙特卡洛法需跟蹤能束直至其被某面元吸收，效率低。為此，本文結(jié)合Gebhart方法（即改進的蒙特卡洛法），先用蒙特卡洛法計算外熱流角系數(shù)，再根據(jù)外熱流角系數(shù)計算輻射傳遞因子。算法數(shù)據(jù)流如圖1所示。

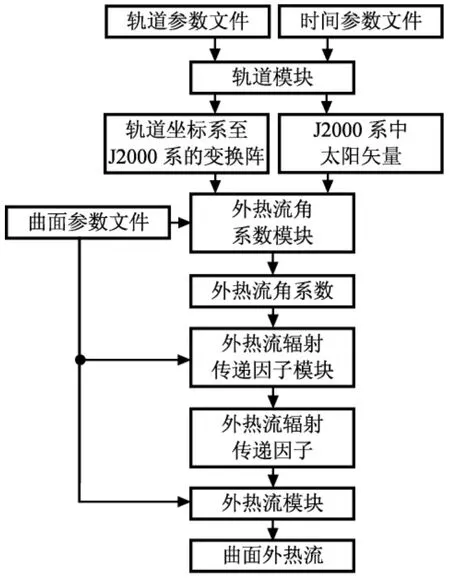
圖1 算法數(shù)據(jù)流Fig.1 Data flowchart of algorithm

2 考慮攝動及太陽矢量變化的外熱流算法

2.1 軌道及太陽位置確定

為計算外熱流角系數(shù)，先須求解太陽、地球及航天器三者位置關(guān)系，本文用SGP4軌道模型確定軌道。SGP4攝動軌道模型采用Brower引力場模型和Lane大氣密度模型，推導(dǎo)出簡化解析式，可用于低軌衛(wèi)星（軌道周期小于225min，高度低于6 000km）的軌道確定［7－8］。

J2000系中太陽矢量坐標（xs，ys，zs）可表示為

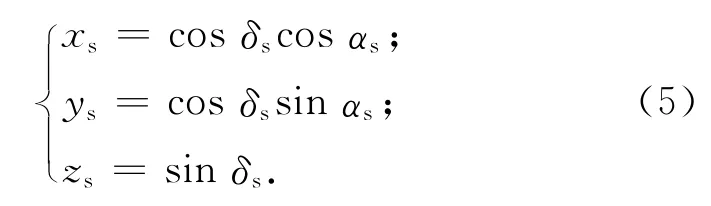
式中：αs，δs分別為太陽赤經(jīng)和赤緯，且

另有

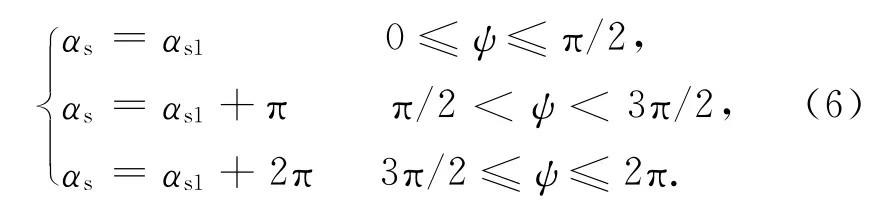
此處：αs1為天球赤道面內(nèi)由春分點矢量轉(zhuǎn)到太陽矢量在赤道面內(nèi)的投影角；I為黃赤交角，且I＝23.5°；ψ為太陽黃經(jīng)，且

其中：t為航天器運行時間；為太陽黃經(jīng)的平均變化率，且＝7.168×10－4rad／h；ψ0為太陽黃經(jīng)初值，且

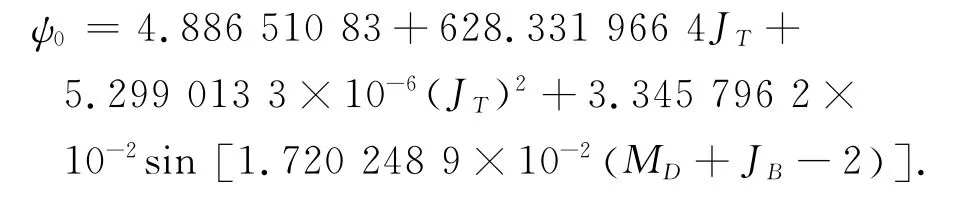
這里：JT為自2000年儒略年首算起的儒略世紀數(shù)；MD為從1月0日至衛(wèi)星發(fā)射月份的儒略日；JB為衛(wèi)星發(fā)射日期所在月份的日數(shù)［2、9］。

軌道確定后，先由J2000系中航天器的位置、速度矢量確定J2000系至軌道坐標系的坐標變換陣。為便于計算，選擇軌道坐標系為蒙特卡洛法的系統(tǒng)坐標系。

傳統(tǒng)方法通過求解地影橢圓方程判斷航天器是否處于地球陰影區(qū)，計算繁瑣［2］。考慮軌道攝動和太陽矢量變化后，地影橢圓實時變化，傳統(tǒng)方法不再適用。由于已知J2000系中航天器位置矢量和太陽矢量，本文用文獻［10］的矢量方法解算。

2.2 外熱流角系數(shù)計算

用蒙特卡洛法計算太陽輻射角系數(shù)時，傳統(tǒng)方法利用假定平面模擬太陽照射方向，以此平面到航天器面元的角系數(shù)替代太陽輻射角系數(shù)［4］。該法需保證假定平面的面積，通用性較差，無法估計假定平面形狀及其到航天器面元距離對計算產(chǎn)生的影響。對此，本文提出改進方法：由航天器面元發(fā)射概率模型隨機產(chǎn)生發(fā)射點，以太陽矢量為發(fā)射方向確定能束；根據(jù)精度要求確定大量能束，判斷能束是否被其他面元遮擋；由未被遮擋能束發(fā)射點處法線矢量與太陽矢量夾角余弦與總能束數(shù)之比得到太陽輻射角系數(shù)。如將航天器劃分為面元N個，每個面元發(fā)射能束Nr條，其中某面元（面積Ai）在某軌道位置處的太陽輻射角系數(shù)φ1i計算流程如圖2所示。

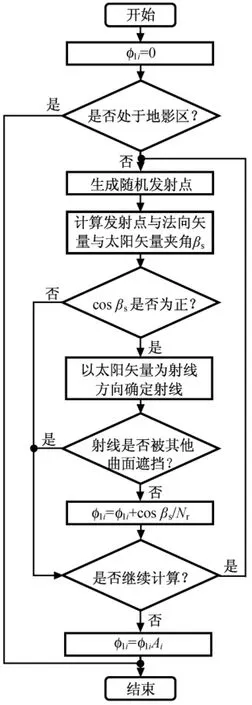
圖2 太陽輻射角系數(shù)計算流程Fig.2 Flowchart of solar radiation view factor algorithm

文獻［5］對應(yīng)用蒙特卡洛法計算地球紅外輻射角系數(shù)和反照輻射角系數(shù)進行了研究。由于兩者計算時均需通過航天器面元能束發(fā)射概率模型生成能束，并判斷能束是否被其他面元遮擋及是否到達地球表面，如單獨計算，耗時較長，而文獻［5］未對此提出改進方案。為提高計算效率，本文對該法作如下改進：用一次循環(huán)同時計算面元Ai地球紅外輻射角系數(shù)φ3i和反照輻射角系數(shù)φ2i，方法流程如圖3所示。

2.3 外熱流輻射傳遞因子計算

圖3 地球紅外及反照輻射角系數(shù)計算流程Fig.3 Flowchart of earth infrared and reflected radiation view factor algorithm

根據(jù)Gebhart方法，航天器面元吸收的外熱流包含直接吸收和經(jīng)其他面元反射后吸收兩部分。由表面間輻射傳遞因子定義，航天器面元Ai吸收的外熱流

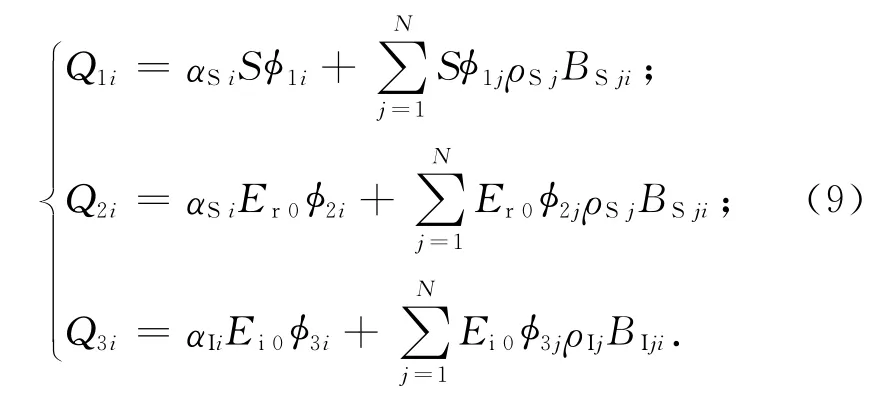
式中：Q1i，Q2i，Q3i分別為面元Ai吸收的太陽輻射、地球反照輻射和地球紅外輻射外熱流；αSi分別為面元Ai在太陽輻射光譜下的吸收率；ρSj為面元Aj在太陽輻射光譜下的反射率；BSji為太陽輻射光譜下的面元Aj到面元Ai的輻射傳遞因子；αIi為面元Ai在紅外輻射光譜下的吸收率；ρIj為面元Aj在紅外輻射光譜下的反射率；BIji為紅外輻射光譜下的面元Aj到面元Ai的輻射傳遞因子。由外熱流輻射傳遞因子定義，有

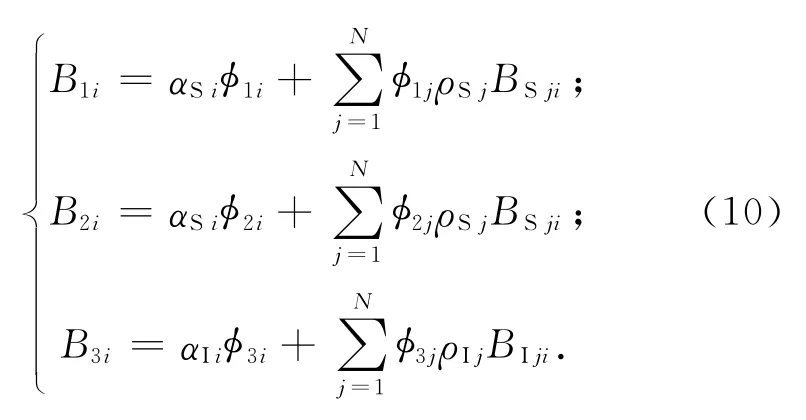
式中：B1i，B2i，B3i分別為面元Ai的太陽輻射、地球反照輻射和地球紅外輻射傳遞因子。計算軌道外熱流時，先求得各面元外熱流角系數(shù)，再由式（10）計算各面元外熱流輻射傳遞因子，最后根據(jù)輻射因子定義計算外熱流。

3 仿真分析

本文以相互遮擋的一圓環(huán)面和一個三角形面（分別如圖4、5所示）進行軌道外熱流計算，并與商業(yè)軟件Thermal Desktop對照，分析太陽矢量變化及軌道攝動對外熱流計算的影響。設(shè)曲面姿態(tài)為對地三軸穩(wěn)定時，軌道坐標系中三角形面三頂點坐標分別為（0，0，0），（1.5，1.5，0），（2，0，0）；圓環(huán)面圓心坐標為（0，0，1）；頂角60°；內(nèi)外半徑分別為1，2m；面元紅外光譜發(fā)射率均為0.9；太陽光譜吸收率均為0.7。取入軌點軌道參數(shù)為軌道傾角30°，軌道周期5 400s，偏心率0.009，升交點赤經(jīng)90°，近地點角距270°，平近角0°，入軌時刻2009－01－01零時整。

因三角形面－Z側(cè)只受太陽輻射外熱流作用，圓環(huán)面＋Z側(cè)僅受地球紅外、反照輻射外熱流作用，相互間不存在遮擋和反射關(guān)系，因此對其計算結(jié)果不作明確說明。

3.1 攝動及太陽矢量變化對外熱流影響

Thermal Desktop軟件根據(jù)入軌點參數(shù)確定軌道位置，不考慮軌道攝動和太陽矢量變化的影響，因此其軌道外熱流在各軌道周期中隨軌道位置變化，為時間的周期函數(shù)。使用外熱流輻射傳遞因子計算入軌后、1d后、7d后及30d后1個軌道周期內(nèi)圓環(huán)面背地側(cè)（Z軸負向）外熱流變化趨勢如圖6～9所示。

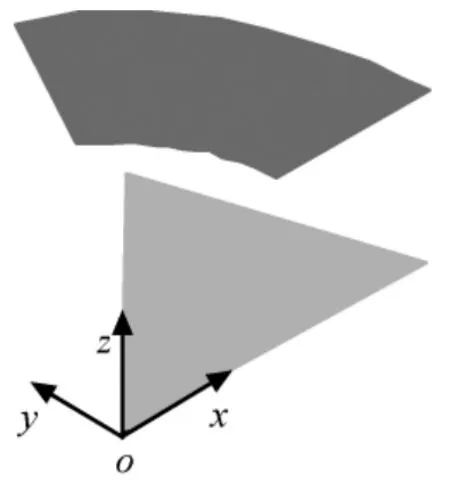
圖4 西南等軸視圖Fig.4 Southwest view

圖5 仰視圖Fig.5 Upward view

由圖6～9可知：在第1周期（90min）內(nèi)，由式（7）可得太陽黃經(jīng)變化約0.06°；由式（5）、（6）所得太陽矢量變化極小，短時間內(nèi)軌道攝動的影響亦可忽略，Thermal Desktop商業(yè)軟件為NASA推廣，不考慮太陽矢量變化和攝動影響時，其計算精度可有效保證，此時本文算法計算結(jié)果與其良好吻合，驗證了本文算法體系的正確性；1d后，Thermal Desktop軟件與本文算法的外熱流變化趨勢一致，但已開始偏離，同時太陽矢量變化對外熱流影響較小；7d后，地球陰影區(qū)所對應(yīng)的平近角變化大于30°，Thermal Desktop軟件已完全不能反映外熱流應(yīng)有的變化趨勢，同時太陽矢量變化也開始影響外熱流計算精度，但并不明顯；30d后，太陽矢量變化導(dǎo)致地影區(qū)對應(yīng)的平近角變化大于60°，但未影響外熱流變化趨勢。

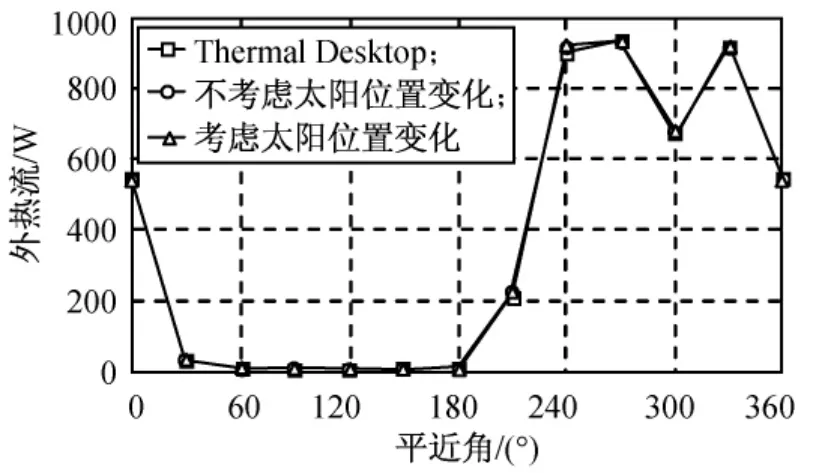
圖6 入軌后1個周期外熱流變化Fig.6 Periodic variation of external heat flux after epoch

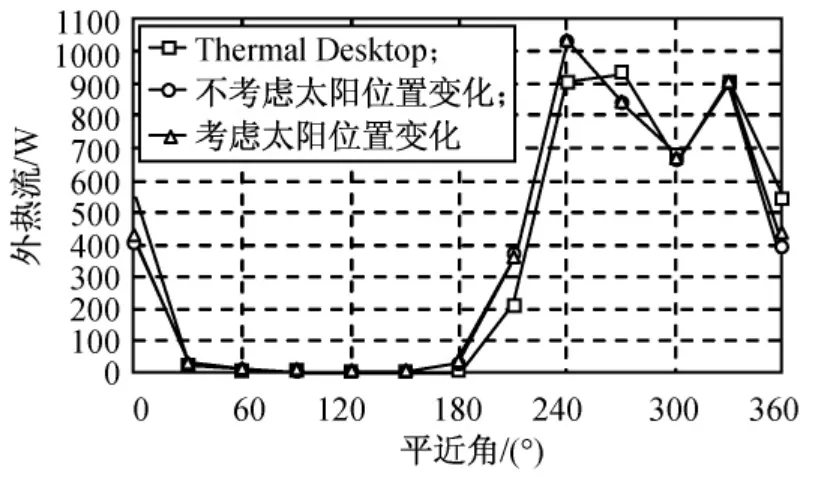
圖7 1d后1個周期內(nèi)外熱流變化Fig.7 Periodic Variation of external heat flux after a day

圖8 7d后1個內(nèi)外熱流變化Fig.8 Periodic variation of external heat flux after 7d

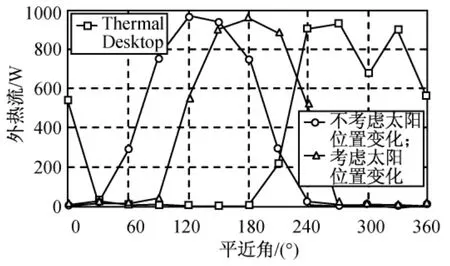
圖9 30d后1個周期內(nèi)外熱流變化Fig.9 Periodic variation of external heat flux after 30d

當軌道傾角為80°時，考慮外熱流輻射傳遞因子的7，30d后1周期內(nèi)外熱流變化分別如圖10、11所示。

由圖10、11可知：當軌道傾角為80°時，7d后，太陽矢量變化對地影區(qū)位置影響較小，并未影響外熱流變化趨勢，而外熱流峰值受到一定影響；30d后，太陽矢量變化導(dǎo)致地球陰影區(qū)所對應(yīng)的平近角變化大于30°，同時外熱流變化趨勢及峰值也產(chǎn)生明顯變化。

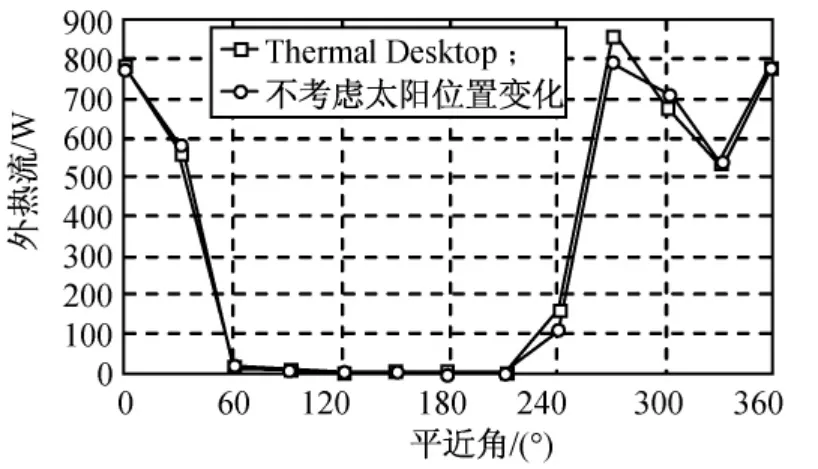
圖10 7d后1個周期內(nèi)外熱流變化Fig.10 Periodic variation of external heat flux after 7d

圖11 30d后1個周期內(nèi)外熱流變化Fig.11 Periodic variation of external heat flux after 30d

3.2 多次反射對外熱流影響

用外熱流角系數(shù)和外熱流輻射傳遞因子計算入軌后1個周期內(nèi)三角形面＋Z側(cè)和圓環(huán)面－Z側(cè)外熱流，結(jié)果分別如圖12、13所示。

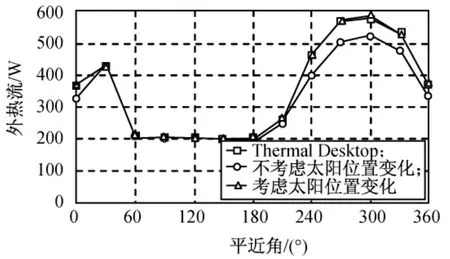
圖12 三角形面＋Z側(cè)外熱流變化Fig.12 Periodic variation of external heat flux of triangle＋Zside after epoch

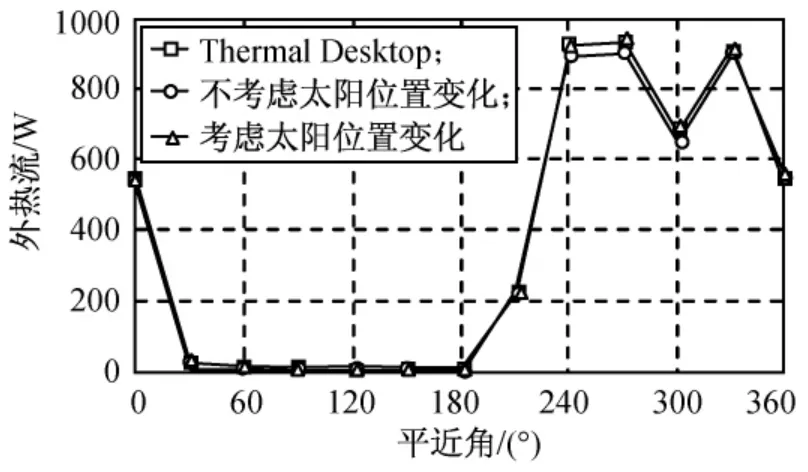
圖13 圓環(huán)面－Z側(cè)外熱流變化Fig.13 Periodic variation of external heat flux of the ring－Zside after epoch

由圖12、13可知：相對外熱流角系數(shù)來說，用外熱流輻射傳遞因子計算與Thermal Desktop軟件更符合，相對偏差約1%。對三角形面＋Z側(cè)，直接投射的太陽輻射外熱流為零，但會吸收部分圓環(huán)面－Z側(cè)反射的太陽輻射外熱流，在日照區(qū)，用角系數(shù)則無法考慮此影響，故與Thermal Desktop軟件相比誤差大于10%；對圓環(huán)面－Z側(cè)，直接投射的地球紅外輻射和反照輻射外熱流為零，但會吸收三角形面＋Z側(cè)反射的地球紅外輻射和反照輻射外熱流，因其量級與太陽輻射外熱流相比較小，在日照區(qū)影響不明顯，但在地影區(qū)影響達20W，用角系數(shù)仍無法考慮此影響。

4 結(jié)論

本文對考慮軌道攝動的外熱流計算進行了研究，重新定義了外熱流角系數(shù)，采用輻射換熱計算中的Gebhart方法，給出了外熱流輻射傳遞因子概念，綜合SGP4軌道模型，研究了考慮攝動與太陽矢量變化的外熱流計算方法，并與Thermal Desktop軟件結(jié)果進行對比。結(jié)果表明：（1）太陽位置變化及攝動影響可忽略時，本文算法計算結(jié)果與Thermal Desktop軟件吻合良好，證明本文算法體系的正確性。（2）一般，航天器面元外熱流存在相互遮擋與反射，用角系數(shù)計算外熱流不能很好地反映真實狀況，故須用輻射傳遞因子計算。（3）軌道攝動對外熱流計算的影響隨在軌運行時間而積累。運行時間較短時，不考慮攝動導(dǎo)致的誤差較小，但隨運行時間增加，攝動對外熱流影響將逐步增大，不考慮攝動的計算結(jié)果將完全不能反映外熱流真實變化狀況。（4）與軌道攝動相比，太陽矢量變化對外熱流的影響較緩慢，但隨在軌運行時間增加其影響亦不可忽略，且具一定復(fù)雜性。根據(jù)入軌點軌道參數(shù)的不同，太陽矢量變化對外熱變化趨勢、外熱流峰值及地影區(qū)位置均會產(chǎn)生影響。太陽輻射在外熱流中所占份額極大，考慮太陽矢量變化的意義重要。（5）軌道攝動和太陽矢量變化均會對地影區(qū)位置產(chǎn)生嚴重影響。由于地影區(qū)只存在地球紅外輻射外熱流，進出地影區(qū)瞬間外熱流會發(fā)生劇烈跳變。因此，為準確計算航天器所受外熱流，須考慮攝動和太陽矢量變化的影響。綜上，一般情況下決定航天器內(nèi)部換熱關(guān)系的導(dǎo)熱熱阻和紅外輻射換熱因子具定常性，航天器所受外熱流是航天器瞬態(tài)溫度場決定因素。準確計算外熱流，可為熱設(shè)計的有效性驗證提供更可靠依據(jù)，本文方法有重要的工程應(yīng)用意義。

［1］張 濤，孫 冰.計算近地軌道航天器空間外熱流的RUD方法［J］.宇航學(xué)報，2009，30（1）：1－6.

［2］閔桂榮.衛(wèi)星熱控制技術(shù)［M］.北京：中國宇航出版社，1991.

［3］趙立新.軌道空間外熱流計算的一種新方法［J］.光學(xué)精密工程，1995，3（6）：80－85.

［4］安敏杰，程惠爾，李 鵬.空間對接機構(gòu)太陽外熱流的計算與分析［J］.上海航天，2006，23（1）：22－26.

［5］翁建華，潘增富，閔桂榮.空間任意形狀凸面的軌道空間外熱流計算方法［J］.中國空間科學(xué)技術(shù)，1994，14（2）：11－18.

［6］余其錚.輻射換熱原理［M］.哈爾濱：哈爾濱工業(yè)大學(xué)出版社，2000.

［7］HOOTS F R.A short efficient analytical satellite theory［R］.AIAA，80－1659.

［8］VALLADO D A.Revisiting spacetrack report＃3［R］.AIAA，2006－6753.

［9］李萬林.衛(wèi)星空間外熱流軌道參數(shù)ψ0，Ω0和ω0計算［J］.中國空間科學(xué)技術(shù)，1993，（6）：58－61.

［10］金學(xué)寬.近地航天器受照角系數(shù)的矢量計算法［J］.宇航學(xué)報，1984，5（1）：69－80.