圓柱斜齒輪浮動凹模冷擠壓成形仿真與實驗研究

薛克敏 李曉冬 李 萍 許 鋒 周結魁 石文超

合肥工業(yè)大學，合肥，230009

0 引言

與直齒輪相比，圓柱斜齒輪具有輪齒重合度高，傳動平穩(wěn)，沖擊、振動小等優(yōu)點，在機械傳動領域有著廣泛的應用。目前對斜齒輪的成形主要采用切削加工，這不僅破壞了金屬的流線性分布，更導致加工后的斜齒輪抗彎、抗疲勞強度大打折扣。對齒輪采取近凈成形工藝，就是通過精密擠壓技術來達到齒廓不需或僅需少許精加工的方法。通過該方法獲得的齒輪鍛件，由于金屬受三向壓應力，其內部疏松、微裂紋等缺陷得以鍛合，工藝塑性得以改善，且金屬纖維沿齒形均勻分布，齒輪的使用壽命顯著提高［1－3］。

然而，圓柱斜齒輪形狀較為復雜且存在一定的螺旋角，當采用擠壓工藝成形時，成形后的齒輪鍛件如何從凹模型腔中順利脫模，成為制約圓柱斜齒輪近凈成形研究的瓶頸。目前國內外學者對圓柱斜齒輪近凈成形工藝進行了研究。Choi等［4］通過上限法分析了斜齒輪導向式和閉式兩種鍛造工藝，并進行了相關的實驗驗證；吳昊等［5］采用閉式溫鍛的工藝模擬了圓柱斜齒輪的成形過程。本文針對某一型號兩種螺旋角的圓柱斜齒輪，采用浮動凹模的工藝進行冷擠壓成形和脫模的研究，探索了在這兩個過程中，影響其成形效果和脫模后斜齒輪精度的因素。

1 圓柱斜齒輪浮動凹模成形工藝分析

和圓柱直齒輪相似，斜齒輪在冷擠壓成形時，也存在成形力過大、齒形角隅部分難充填等困難。采用浮動凹模結構，可有效改善摩擦條件，改善坯料在模具型腔的充填情況，降低成形載荷，減少模具的磨損等。

當采用傳統(tǒng)的閉式擠壓成形時，下沖頭及凹模固定，上沖頭以速度v向下運動，如圖1a所示。毛坯的主要流動方向是朝下的，凹模相對于毛坯向上運動，毛坯在擠壓過程中受到凹模施加的摩擦力作用，該摩擦力方向與金屬運動方向相反，隨著擠壓過程的進行，摩擦力會越來越大，最后導致斜齒輪的上下角隅處難以充填。若將凹模改為可浮動的，如圖1b所示，在擠壓變形開始時，凹模在上沖頭的壓力下，隨其以同一速度v下行。整個變形過程中，凹模對坯料產生摩擦力，但該力方向沿軸向向下，與金屬運動方向相同，最終可促進齒形角隅部分的充填［6］。

圖1 模具工裝對比圖

由于圓柱斜齒輪存在一定的螺旋角，在擠壓成形和脫模時，下沖頭會在凹模齒腔的導向作用下，自動地沿著螺旋角方向邊旋轉邊沿軸向向上運動，為方便下沖頭運動，可在其底部安裝推力球軸承。

2 工藝過程有限元模擬

為了進一步探索圓柱斜齒輪在浮動凹模冷擠壓成形過程中金屬流動規(guī)律以及影響脫模后齒輪精度的因素，本文以某一型號的兩種圓柱斜齒輪為對象進行了相關研究。斜齒輪的基本幾何參數如下：齒數為22，法面模數為2.5mm，壓力角為20°，齒頂高系數為1.0，頂隙系數為0.25，螺旋角分別為22°和32°。

2.1 有限元模型的建立

運用Deform－3D有限元軟件，采用剛塑性有限元法，對圓柱斜齒輪浮動凹模冷擠壓成形過程進行計算機仿真模擬。模擬時坯料所選材料為20CrMnTi，將模具視為剛體，不發(fā)生彈塑性變形，坯料和模具的初始溫度均設定為室溫25℃。為精確建模及節(jié)省計算時間，劃分網格時，對圓柱斜齒輪的齒形部分進行局部細化，網格總數為1.2×105，齒形與其余部分網格尺寸比為1∶10，建立的有限元模型如圖2所示［6］。

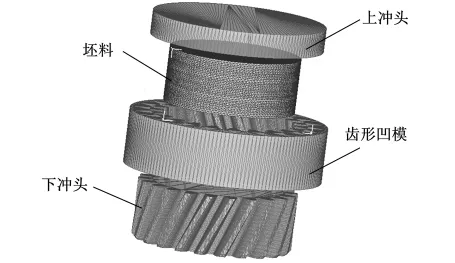
圖2 斜齒輪模具與坯料的有限元模型

2.2 摩擦模型的建立

在進行有限元模擬及物理實驗時，需正確處理毛坯金屬與模具之間的摩擦關系［7］。不考慮接觸面上的黏合現(xiàn)象，本文采用應用比較廣泛的庫倫摩擦模型，其數學表達式為

式中，f為與速度方向相反的摩擦力；μ為摩擦因數；Pn為法向壓力。

3 浮動凹模成形過程模擬與實驗

3.1 實驗過程

為了降低實驗成本，簡化實驗過程，本次實驗毛坯材料選用工業(yè)純鉛。分別制作了螺旋角為22°和32°的兩套簡易模具來作工藝對比。在擠壓成形時為便于斜齒輪下沖頭自由地在齒形凹模內沿軸向和圓周方向運動，在設計模具時，下沖頭齒頂圓直徑較標準齒形小0.05mm，如圖3所示［8－9］。成形設備是2MN 液壓機。

圖3 下沖頭齒形示意圖

3.2 模擬與實驗結果分析

表1所示為采用傳統(tǒng)閉式擠壓工藝和浮動凹模冷擠壓工藝時，螺旋角分別為22°和32°的圓柱斜齒輪不同壓下量的成形效果對比圖。現(xiàn)以前者為例進行成形分析。從表1中第1組圖可以看出，若采用傳統(tǒng)的閉式擠壓工藝成形圓柱斜齒輪，由于上下沖頭與坯料表面的摩擦作用，毛坯在擠壓過程中表現(xiàn)出中部徑向流動速度快，上下端部流動較慢的特征。當壓下量達到30%時，鍛件中部出現(xiàn)一定量的鼓形趨勢，但不明顯；當壓下量達到60%時，形成鼓形的趨勢加劇，上下端部徑向流動明顯滯后，因此在后續(xù)成形過程中，主要完成上下端部及其角隅部分的充填。若對其采用浮動凹模工藝成形（如表1中第2、第3組圖所示），由于浮動凹模改變了摩擦力的方向，使其與金屬的流向相同，從而加快了毛坯的中下部金屬的徑向充填速度。當壓下量達到30%時，已出現(xiàn)上端徑向流動滯后于下端，鍛件略微呈現(xiàn)梯形；當壓下量達到60%時，形成梯形的趨勢明顯加劇，鍛件下端及中部齒形已經充填大部分，此時上端齒形剛開始充填，因此在后續(xù)成形過程中，主要完成上端部齒形及其角隅部分的充填。

對于螺旋角為32°的圓柱斜齒輪，在浮動凹模冷擠壓工藝下（如表1中第4、第5組所示），其成形規(guī)律與螺旋角為22°時相似。

圖4所示為兩種斜齒輪在傳統(tǒng)閉式擠壓工藝和浮動凹模冷擠壓工藝下成形載荷隨時間增量步變化曲線。圓柱斜齒輪采用浮動凹模冷擠壓工藝時，整個冷擠壓過程所需的成形力相對于傳統(tǒng)閉式擠壓工藝明顯降低。螺旋角為22°和32°的圓柱斜齒輪采用浮動凹模冷擠壓工藝成形時載荷分別為6.0MN和7.1MN，而采用傳統(tǒng)閉式擠壓工藝時兩者的成形載荷分別為8.5MN和9.5MN。相比之下，采用浮動凹模工藝成形時工作載荷可分別降低約30%和25%。

注：第1組為22°螺旋角傳統(tǒng)工藝等效應變圖；第2組為22°螺旋角浮動凹模成形等效應變圖；第3組為22°螺旋角浮動凹模成形實驗效果圖；第4組為32°螺旋角浮動凹模成形等效應變圖；第5組為32°螺旋角浮動凹模成形實驗效果圖。

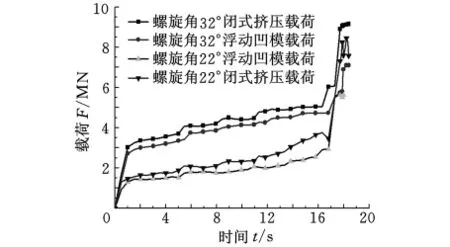
圖4 成形載荷－時間曲線圖

4 脫模過程模擬與實驗分析

圓柱斜齒輪在脫模時若工藝參數控制不當，勢必會使成形好的鍛件產生破壞性的變形，導致其無法修復。而影響脫模過程的因素較多，其中比較顯著的有摩擦因數和螺旋角。脫模時，單個齒形的受力情況如圖5所示。

圖5中，F(xiàn)為下沖頭施加的脫模力，方向豎直向上；F1、F2分別為F沿著齒形方向和垂直于齒形方向的分力；β為斜齒輪螺旋角；Fz為齒形在擠壓成形時，由于脹形而對凹模產生的作用力，該力的方向應垂直于齒形，對于既定的工藝，F(xiàn)z可取常數（其值近似等于當β＝0，μ＝1而其他參數不變時的脫模力，通過數值模擬，浮動凹模成形工藝下Fz約為182.61kN）。

假設在脫模時，斜齒輪鍛件能勻速被頂出，則有下列受力平衡關系：

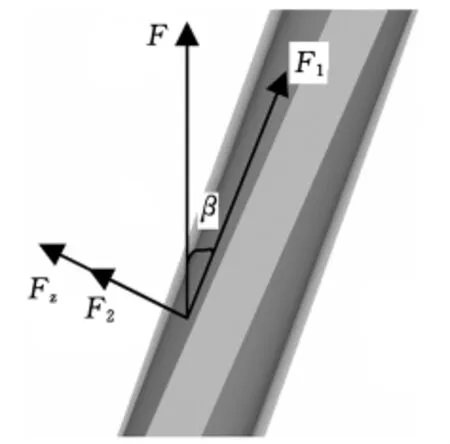
圖5 單個齒形受力圖

式中，F(xiàn)、β、μ為變量；Fz為常數。

4.1 摩擦因數對脫模過程的影響

當螺旋角β一定時，由式（1）可得F與μ有下列關系式：

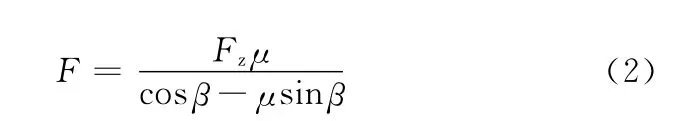
當摩擦因數μ分別取0.10、0.12、0.14時，通過式（2）計算可得表2。

表2 脫模力理論計算表 kN

從表2可以看出，當螺旋角β不變時，脫模力隨摩擦因數μ的增大而增大。圖6為在三種摩擦因數下，圓柱斜齒輪通過數值模擬所獲得的脫模力隨時間變化曲線圖，由模擬曲線可以看出，當μ分別取0.10、0.12、0.14時，螺旋角為22°的圓柱斜齒輪脫模力分別在20kN、24kN、29kN上下波動；螺旋角為32°時，其波動值則分別為22kN、27kN、33kN。由此可見，數值模擬與計算結果是較為吻合的，在一定程度上驗證了數值模擬的可靠性。

4.2 螺旋角對脫模過程的影響

當摩擦因數μ一定時，由式（1）可得F與β有下列關系式：

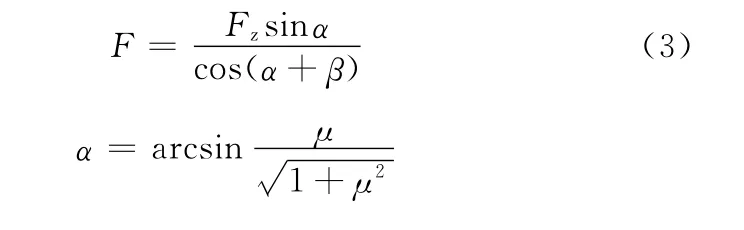
圖6 脫模力－時間變化曲線圖

圖7為摩擦因數μ＝0.10時，脫模力F與螺旋角β之間的關系曲線圖。從圖7可以看出，脫模力隨著螺旋角的增大而增大，且增大的趨勢越來越快。當β＝22°和32°時，脫模力分別達到約20kN和23kN。

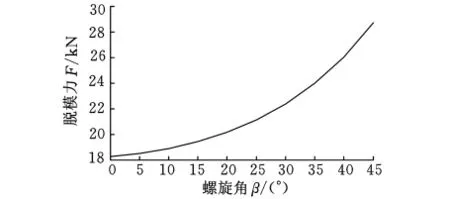
圖7 μ＝0.10時，F(xiàn)與β曲線圖

4.3 模擬與實驗結果對比

表3所示為斜齒輪鍛件脫模過程中模擬與實驗結果對比分析。從速度場可以看出，齒輪鍛件在脫模時，金屬的流動速度均沿著齒形方向，且大小相近，這說明在脫模過程中，齒形在凹模的導向作用下，自動地沿著螺旋方向做剛性旋轉運動，幾乎不產生塑性變形，可有效地保證脫模后斜齒輪鍛件的精度。從應變場可以看出，螺旋角為22°的斜齒輪鍛件脫模后，等效應變主要集中在上下齒形的角隅部分，其余部分幾乎沒有變形；當螺旋角增大到32°時，等效應變除了集中在齒形角隅部分外，中部齒形也出現(xiàn)微小的應變。因此，隨著螺旋角的增大，脫模后的斜齒輪鍛件精度會有一定的下降。

從表3中實驗效果圖可以看出，脫模后的斜齒輪鍛件齒形較飽滿，無角隅塌陷等缺陷，在保證使用要求的前提下，只需對齒輪鍛件進行稍微的倒角、打磨處理即可保證精度要求［10－11］。

5 結論

通過數值模擬與實驗相結合的方法，對兩種不同螺旋角的圓柱斜齒輪浮動凹模冷擠壓成形及脫模進行對比分析，得出以下結論：

（1）圓柱斜齒輪采用浮動凹模工藝可有效改變摩擦力方向，降低成形載荷，與傳統(tǒng)工藝相比，螺旋角為22°和32°的兩種斜齒輪，成形力分別下降約30%和25%。

（2）通過數值模擬和鉛試樣實驗，揭示了脫模過程中斜齒輪鍛件沿著齒形螺旋方向做剛性旋轉運動的現(xiàn)象，在一定程度上避免了脫模時凹模齒腔對鍛件齒形產生的破壞性變形。

（3）影響圓柱斜齒輪成形的因素較多，其中比較顯著的是螺旋角和摩擦因數，總的來說，鍛件精度隨著螺旋角和摩擦因數的增大而有所降低。因此，在保證使用要求的前提下，需對鍛件進行一定的表面處理以保證其精度。

［1]海錦濤.塑性成形技術的新思路［J］.中國機械工程，2000，11（1／2）：180－182.

［2]王崗超，薛克敏，許峰，等.齒腔分流法冷精鍛大模數圓柱直齒輪［J］.塑性工程學報，2010，17（3）：18－21.

［3]胡成亮，劉全坤，王強，等.直齒輪剛性旋轉兩步成形工藝仿真與試驗［J］.農業(yè)機械學報，2008，39（1）：161－164.

［4]Choi J C，Choi Y，Tak S J.The Forging of Helical Gears：Comparisons of the Forging Processes［J］.International Journal of Mechanical Sciences，1999，41（6）：725－739.

［5]吳昊，伍萬斌，薛克敏.圓柱斜齒輪閉式溫鍛數值模擬［J］.合肥工業(yè)大學學報，2008，31（1）：96－99.

［6]江雄心，萬平榮，扶名福.齒輪精鍛的數值模擬與實驗研究［J］.塑性工程學報，2002，9（1）：62－65.

［7]俞漢清，陳金德.金屬塑性成形原理［M］.北京：機械工業(yè)出版社，1999：151－153.

［8]劉華，席慶坡，霍艷軍，等.圓柱齒輪精鍛數值模擬及輪齒修形規(guī)律［J］.西安交通大學學報，2004，38（11）：1186－1189.

［9]朱家誠，王純賢，等.機械設計基礎［M］.合肥：合肥工業(yè)大學出版社，2003：49－54.

［10]胡成亮，劉全坤，王強，等.基于灰色關聯(lián)和模糊邏輯的齒輪鍛模多目標優(yōu)化設計［J］.中國機械工程，2007，17（14）：1739－1742.

［11]陳永久，蒿敬恪，杜梅.機械加工技術［M］.北京：人民郵電出版社，2008：154－160.